三维聚焦破碎波相关特性的试验研究——单频聚焦

王 磊，李金宣*，杨金凤，柳淑学，刘 元

(1.大连理工大学 海岸和近海工程国家重点实验室，大连116024；2.大连理工大学 建设工程学部，大连 116024)

波浪破碎是海洋中常见的物理现象，是许多海洋工程和海岸工程问题的重要影响因素，破碎损耗是海浪模型能量耗散项中所考虑的重要物理机制，波浪破碎问题长期以来受到众多学者的关注。

Longuet-Higgins[1]最先提出利用波能聚焦的方法在实验室中生成破碎波浪，即通过不同频率的组成波间相互调制，使波浪在指定位置、指定时刻波峰达到最大，波陡达到极限值而发生破碎。Rapp和Melville[2]通过波能聚焦的方法，在实验室二维水槽中生成了深水破碎波浪，分析了波浪在传播过程中波浪频谱的演化特性，研究发现破碎能量损失主要来自于高频部分；Kway等[3]同样通过波能聚焦的方法，在深水中产生了崩破波和卷破波，他们考虑了不同的频谱形式等波陡分布、等波幅分布和PM谱。Drazen[4]采用波浪聚焦的方法产生破碎波，提出了破碎的能量耗散率测量方法和破碎引起的湍流统计学测量方法。这些实验主要集中于二维波浪实验[5]，在实际的海浪当中，波浪传播是多向的，而波浪传播的多向能够显著地影响聚焦波浪破碎的运动学和动力学特征，并且对破碎波高和其他的波面参数有很大的影响，所以在实际的工程中必须考虑多向波对波浪的动能和作用于海上结构物的力的影响[6-7]，因此深入研究三维聚焦波浪方向分布对破碎问题是非常重要的，并且也更具有实际应用价值[8]。She等[9-10]利用单一频率不同方向波浪聚焦和多频率不同方向波浪聚焦形成的极限波，研究了方向分布对聚焦破碎的影响，结果显示波浪的方向分布对临界破碎波浪的波高、峰值、波前陡度和波面的不对称性具有明显的影响。同时，Johannessen[11]在Baldock等[12]和Baldock[13]的基础上，采用数值模拟和物理实验模拟的方法研究了三维线性波峰和极限波的波浪特性。研究结果表明，引入波浪的方向分布特性可减小波浪之间的非线性相互作用。

为了进一步研究多向聚焦波浪的特性，本文基于线性聚焦理论，采用波能聚焦方法，在港池中成功模拟了三维聚焦极限波浪和破碎波浪。本文主要研究方向分布范围对单频聚焦波浪波面特性的影响，考虑不同方向分布范围时，波浪破碎过程中其破碎指标、能量损失等特征变化。

1 试验介绍

1.1 聚焦波产生方法

根据Rapp和Meville[14]产生二维聚焦波浪的方法，考虑方向分布的影响来产生三维聚焦波浪。由线性叠加理论，在任意点处波浪自由表面可以表示为不同频率和不同方向的规则波叠加的结果，即

(1)

式中：aij为波幅；fi为频率；ki为波数；θj为方向角；φij为组成波初相位；Nf和Nθ分别为组成频率数和方向数。组成波频率fi和波数ki满足线性色散关系

(2)

式中：g为重力加速度；h为水深。

如果假定波浪在指定时刻t=tb时，聚焦于位置(xb,yb)，即各组成波在该处叠加，要求

cos(kixbcosθj+kiybsinθj-2πfitb-φij)=1

(3)

则各组成波的初相位应满足下式

φij=kixbcosθj+kiybsinθj-2πfitb+2mπ(m=0,±1，±2，…)

(4)

将式(4)代入式(1)，并取m=0，这时可把波浪的波面η(x,y,t)写成

(5)

在式(5)中，各组成波的波幅aij取决于波浪的频谱分布形式和方向分布，假设聚焦振幅为A，则有

(6)

本实验中仅考虑单频聚焦，故Nf=1，即fi=fp。令GA(θ)为方向分布系数，满足下式

(7)

式中：θmax为波浪的最大方向角；s为方向分布集中度参数。本实验中s取0值，意味着组成波波幅在各个方向均匀分布。则本实验中各组成波的波幅aij可表示为

aij=AGA(θj)

(8)

图1 单频聚焦波的波面Fig.1 Wave surface of single frequency focused wave

图1给出了本实验中一组典型的单频聚焦波的波面。从图中可以看出，由于为单频率波浪，不同方向波速相同，因此波浪以同心圆弧的形式逐渐向聚焦点集中，在聚焦点处形成波高较大的大浪，随后又以弧形散开。

1.2 实验布置

本实验是在大连理工大学海岸和近海工程国家重点实验室的多功能港池中进行的。水池长54 m、宽34 m、深1.3 m，有效面积为长45 m、宽28 m，最大有效水深0.7 m。在港池一端配有液压伺服多向不规则造波机，造波机是由70块宽0.4 m、高1.0 m造波板组成，造波机通过微机控制，能够保证很好的重复性。为了防止波浪的反射，在港池的末端设有消能装置，以减少波浪的反射。

实验布置图如图2所示，波浪聚焦点设置在水池中心线上距造波板9.0 m处，考虑到波浪呈圆弧形式聚焦，试验中浪高仪布置在以聚焦点为中心的不同半径圆弧上，聚焦前区域圆弧分别标注为I、II、III和IV，对应半径分别为：1.5 m、2.5 m、4.5 m和7.0 m。圆弧上测点和聚焦点连线与水池中线分别呈α=0°、10°、20°、30°、40°。在聚焦点后区域，同样布置相同数量浪高仪，其位置与聚焦点前区域关于聚焦点反对称，对应圆弧分别标注为I′、II′、III′和IV′。由于聚焦波浪场关于水池中线对称，浪高仪仅布置在中线一侧，测点A和B用于检验波浪场的对称性。整个试验共布置了55根浪高仪，如标号II 10°的浪高仪在圆弧II上和聚焦点连线与中心线呈α=10°的位置。实验前，浪高仪均经过严格的检测和率定，性能可靠。实验每组参数将被重复3遍以保证实验的准确性。每次实验需有12～15 min的时间间隔，以保证港池水面恢复平静。

图2 实验布置图Fig.2 Experimental arrangement

表1 试验参数Tab.1 Test parameters

表1给出了单频聚焦试验所采用的波浪参数。试验中考虑了三个方向分布范围，最大波浪方向角度θmax分别为30°、45°和60°，和不同的波浪频率。组成波在方向分布范围[-θmax，θmax]内均匀分布，组成波数Nθ=100、试验水深h为0.5 m。对于固定的最大方向角度和频率，从小到大逐渐增大输入聚焦波幅A，已得到未破碎聚焦波、临界破碎波以及不同破碎强度的破碎波。

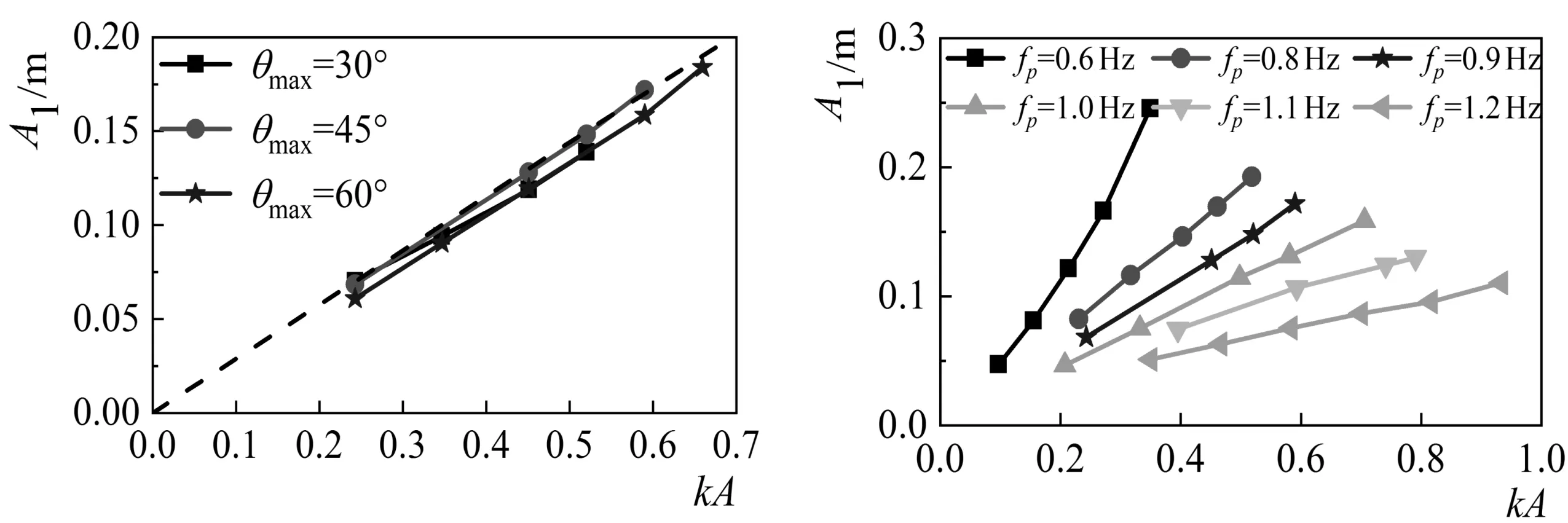
3-a fp=0.9 Hz3-b θmax=45°图3 聚焦波幅随输入聚焦波幅的变化关系Fig.3 The relationship between the focus amplitude and the input focus amplitude

图3给出了几组典型未破碎波实际聚焦波幅随输入聚焦波幅变化的曲线，其中A为输入波幅，A1为输出波幅。从图中可以看出，在不同的频率和不同的入射方向角度范围下，实际的聚焦波幅与输入的聚焦波幅之间保持了良好的线性关系，波浪非线性不是很明显。另外也可以注意到方向分布较宽时能得到的最大波幅稍大些。

2 单频多向聚焦波浪分析结果

2.1 比波高分布图

图4和图5给出了非破碎工况(fp=0.9 Hz，A=0.07 m)的波浪场波高分布以及不同传播方向(α)上的波峰最大值的变化。从图4可以看出，对于未破碎波，不同方向分布宽度时，都在聚焦点处取得波高最大值，说明波浪实际聚焦位置与假定的聚焦位置吻合较好。另外，方向分布范围越小，能量越向主方向集中，靠近中心线上的波高越大；方向分布范围大时，场内波浪分布较均匀，仅在聚焦点外波高迅速增大。

4-a θmax=30°4-b θmax=45°4-c θmax=60°图4 未破碎时比波高分布图(fp=0.9 Hz,A=0.07 m)Fig.4 Distribution of specific wave height when not broken (fp=0.9 Hz,A=0.07 m)

5-a α=0°5-b α=10°5-c α=20°

5-d α=30°5-e α=40°

对比聚焦前后对称位置上的波高可以发现，主方向上测点聚焦后波高有所增大，而方向偏离主方向较大时，波高有所减小。这个现象在图5中更为明显，在主传播方向α=0°上，聚焦点后测波高要比前侧大；而α=40°上，聚焦点后测波高要比前侧小。这个现象对于方向分布较宽时最为明显。该现象可能是由于波浪聚焦过程中波浪间相互作用，改变了波浪的传播方向，使向两侧传播的波浪向主方向集中。

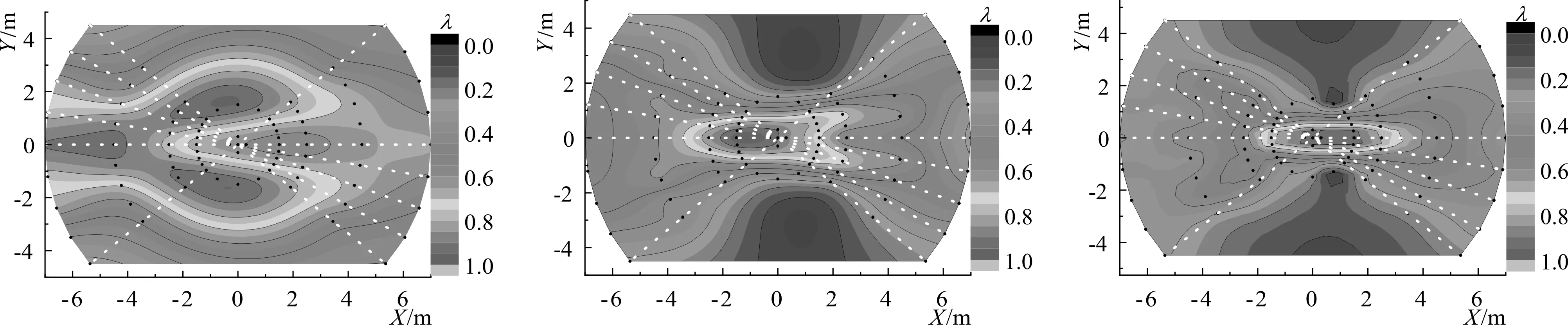
6-a θmax=30°6-b θmax=45°6-c θmax=60°图6 破碎时比波高分布图(fp=0.9 Hz, A=0.20 m)Fig.6 Distribution of specific wave height when broken (fp=0.9 Hz, A=0.20 m)

图6和图7给出了破碎工况(fp=0.9 Hz，A=0.20 m)的波浪场波高分布以及不同传播方向(α)上的波峰最大值的变化。对于破碎情况(如图6)，波高分布有明显不同。由于破碎发生，波高不在关于聚焦点对称，其中方向分布范围较小时，最为明显，由于该情况能量集中，波浪在达到聚焦点前就开始破碎，主方向上聚焦点对称位置波高变化明显，说明主方向上能量损失要比其他方向要大。当方向分布范围较大时，相同聚焦波高情况下，破碎位置更接近聚焦点，对于图示工况破碎强度相对较小，破碎后波高变化不是十分明显，甚至由于聚焦作用，主方向的波高还有所增大。通过图7各传播方向波峰变化能够清楚看出该现象。

7-a α=0°7-b α=10°7-c α=20°

2.2 几何破碎指标

图8 波面参数的定义Fig.8 Definition of wave surface parameters

波浪聚焦过程中波浪波面陡度不断增加，当其达到某一临界值时，波浪发生破碎，这临界值是研究波浪破碎的重要指标。Kjeldsen等[15]提出了几个波面参数来作为波浪破碎的几何指标：整体波陡：εT=2πηmax/gT2；波前陡度：ε=2πηmax/gT1T；波后陡度：δ=2πηmax/gT2T，其中g为重力加速度，这些参数的定义如图8，在图中ηmax为该点波峰最大值，波高H和周期T的定义采用下跨零点定义。图9给出了未破碎情况下，不同方向分布范围中心线上各点的波前陡度、波后陡度和整体波陡变化。可以看出，当破碎未发生破碎时，对于波浪陡度，由于波幅较小，在波浪聚焦过程中，随着各组成波浪的叠加，波前陡度、波后陡度和整体陡度都逐渐增加，直至聚焦点处达最大值后开始逐渐减小。并且当方向分布范围越小时，产生的聚焦波浪越陡。这是由于方向分布范围越小，波浪更加聚集于一个较小的传播角度范围内，因而各陡度也相应较大。由于此时波浪更陡，所以在图3中方向分布范围小时得到的最大非破碎波高要小。

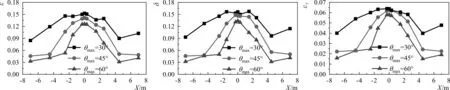
9-a 波前陡度ε9-b 波后陡度δ9-c 整体波陡εT图9 不同方向分布范围中心线上各点的波面参数(fp=0.9 Hz,A=0.07 m)Fig.9 Distribution range in different directions, wavefront parameters at each point on the center line (fp=0.9 Hz, A=0.07 m)

图10给出了破碎情况下，不同方向分布范围中心线上各点的波前陡度、波后陡度和整体波陡变化。从图中可以看出，当波浪发生破碎时，相同波幅下，方向分布范围越大，破碎指标最大值发生在聚焦点附近；方向分布范围越小，破碎指标最大值越前移，说明破碎前移，破碎后，能量损失，波高减小，波前陡度和波后陡度均减小。

10-a 波前陡度ε10-b 波后陡度δ10-c 整体波陡εT图10 不同方向分布范围,中心线上各点的波面参数(fp=0.9Hz, A=0.20 m)Fig.10 Distribution range in different directions, wavefront parameters at each point on the center line (fp=0.9 Hz, A=0.20 m)

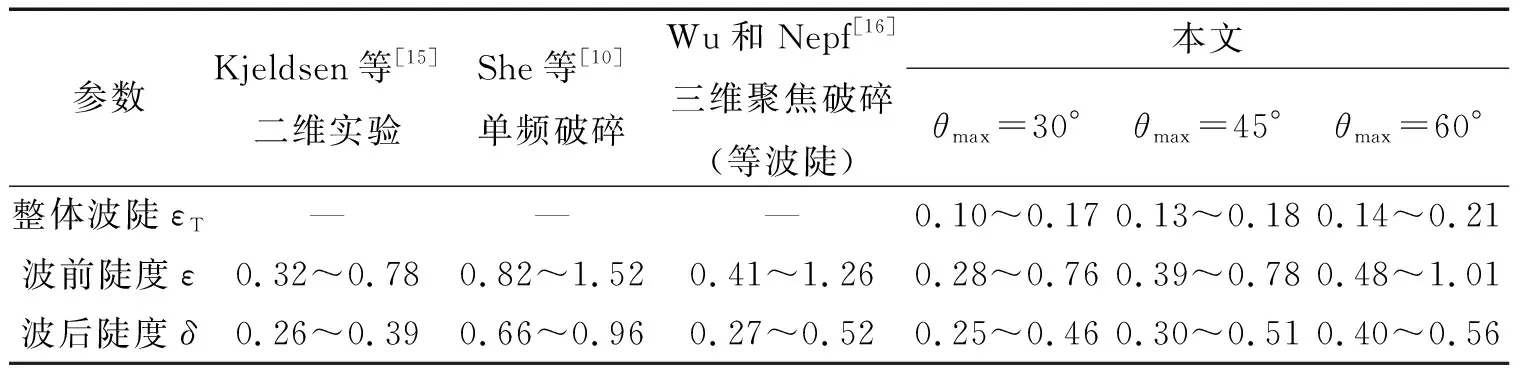
表2 几何破碎指标比较Tab.2 Comparison of geometric breaking indexes

表2中列出了不同实验给出的波前陡度、波后陡度和整体波陡分析结果，取值范围为破碎时的值至最大值。其中She等[10]通过直接法求得波浪参数，本实验和Kjeldsen等[15]、Wu和Nepf[16]都是采用间接方法求得相关破碎指标。通过比较可以看出，She等[10]通过直接方法求出的破碎指标要比其他集中情况要大，本试验中等波幅分布的结果与Wu和Nepf[16]实验中聚焦破碎结果很接近，而Kjeldsen等[15]的二维试验结果相对三维结果偏小。此外，从实验结果来看，方向分布范围对整体波陡、波前陡度和波后陡度等破碎指标有明显影响，方向分布越宽破碎指标值越大。但整体来看几何破碎指标随波浪参数变化明显，并不能很好地描述波浪破碎。

2.3 能量损失

本节将计算聚焦波破碎后的能量损失。对于三维波浪，波浪的总能量可以对某一断面上的波高积分求得，由于本实验仅测得[-40°，40°]范围内的入射能量，则总能量如下

(9)

式中：r为断面半径；T0为采集时间；η为波面；Na为圆弧上浪高仪个数；Nj为时间点数。

关于聚焦点对称圆弧上能量差认为是波浪破碎中的能量损失，能量耗散率D定义为

(10)

表3 比例系数βTab.3 Proportional coefficient β

式中：E前和E后分别为聚焦前和聚焦后的能量，本实验通过IV和IV′圆弧上测点积分求得。E总为实际聚焦的总能量，由于本实验仅测得[-40°，40°]范围内的入射能量，为了得到总能量，事先通过数值模拟的方法，求得[-40°，40°]范围内能量占总能量比重β。表3给出了不同方向分布范围时，β值的变化。可以看出，方向分布最大角度为30°时，β为0.94，说明试验测点布置范围基本覆盖了整个入射波浪场。当方向分布最大角度为60°时，β为0.71，说明仍有部分波浪不在测量范围内。

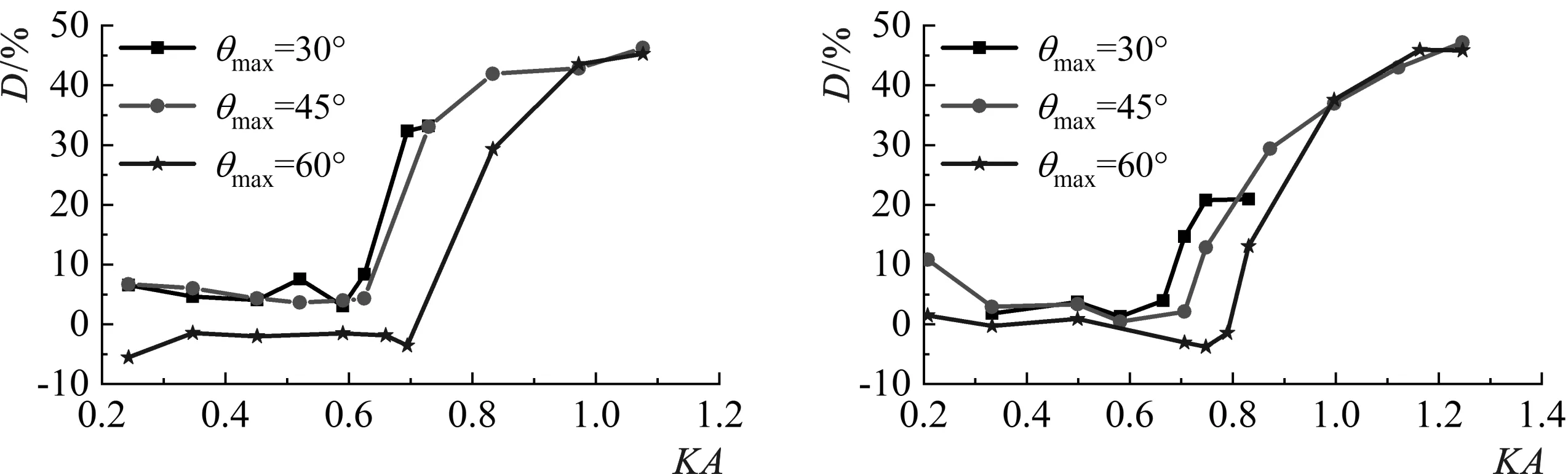
11-a fp=0.9 Hz11-b fp=1.0 Hz图11 不同聚焦波幅下的能量损失Fig.11 Energy loss under different focusing amplitude

聚焦总能量可由E总=E前/β求得，通过公式(10)可计算破碎波的能量损失率。图11给出了不同方向分布宽度时，破碎能量损失随波陡的变化。从图中可以看出，当波陡较小时，波浪没有发生破碎，能量损失率随波陡变化不大，这部分损失可能是由于底摩擦引起的。另外可以注意到对于不破碎情况，方向分布范围为θmax=60°时，能量损失为负值，这个可能是跟2.1节中介绍的现象有关，波浪聚焦过程中波浪传播方向主方向集中，IV’断面测得的能量要比IV断面大，造成聚焦后能量反而增大的现象。

当波陡增大时，波浪开始发生破碎，破碎的能量损失随波陡增大而增大。方向分布宽度大时，会产生更大的能量损失率，本实验中θmax=45°和60°时，最大的能量损失率可达到约45%；而θmax=30°时，波浪的能量损失率要小。

3 结语

本文通过方向聚焦的方法在港池中成功模拟了三维单频聚焦波浪。研究了方向分布范围对波浪聚焦和破碎的影响。试验研究结果表明：

(1)三维波浪聚焦过程中，波浪的传播方向会有一定的改变，两侧波浪向主方向集中。方向分布越宽，该现象越明显。

(2)方向分布宽度对波浪几何破碎指标也有一定的影响，通常方向分布宽度越大，整体陡度、波前陡度和波后陡度都有偏大的趋势。说明方向分布宽，波浪越不容易破碎，能得到的最大波幅也越大。

(3)三维波浪的破碎能量也受方向分布的影响，本文方向分布θmax=45°和60°时，最大的能量损失率可达到约45%；而θmax=30°时，由于方向分布范围小，能量越向主方向集中，波浪的能量损失率越小。