电厂取排水玻璃钢管受波浪力数值模拟研究及改善措施

罗子湛，贾 丽，戈龙仔，管 宁

(1.中国华电科工集团有限公司，北京100160; 2.交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室，天津 300456)

滨海电站取排水方式主要有管道和箱涵两种，采用钢管管道时，受材质影响需要对其进行内外防腐、阴极保护和定期维修等措施，其防腐和运行维护费用都很高。采用混凝土箱涵时，其自重大、难吊装、对地基处理要求高、断面尺度大而长度短、海生物极易附着，这些导致清理礁石和施工难度大、费用高[1]。新型的玻璃钢管具有重量轻、耐腐蚀、防海生物附着、使用寿命长等技术优点，目前在取排水工程中的应用日益广泛。

但在淤泥质粘土中玻璃管道受波浪荷载循环作用下，可能会发生海床覆盖层液化，使埋设在淤泥层中的海底管道的受力状态发生变化，从而出现上浮或下沉的现象，对管道的稳定性产生影响[2]，同时传递到玻璃钢管上的波浪荷载也可能影响到本身的强度，因此有必要了解该状态下管道受力情况，目前国内外学者在管道受力问题上已经开展了一系列工作，但很少考虑施工回填过程中的材料介质对管道的影响，以及运营期波浪循环荷载作用下，回填料中管道的受力特性。例如夏鹏飞[3]通过玻璃钢管水流阻力试验，对水力光滑管区和紊流水力过渡区的玻璃钢管阻力系数分布规律提出了计算公式与曲线图表。潘东子[4]以孔隙水压力为着手点，研究了部分埋入海床的管道圆周上孔隙水压力幅值随波高和周期的变化，并得出埋置深度对浮托力的影响。尹胜强[5]基于CFD开源程序库OpenFOAM，采用不可压缩粘性两相流模型,以VOF方法捕捉自由面研究防波堤水动力特性。刘靖[6]利用二维FEM软件研究了海底管道在粗砂和细砂条件下管道所受应力规律。李玉成[7]采用三步有限元法，结合LES方法和N-S方程，模拟海底管道受力和海底管道周围流场的情况。Zhao[8]等应用FEM方法追踪任意的Lagrange-Euler格式自由运动表面方法，计算出特定条件下作用于海底管道上的波浪力。Zhang[9]采用FEM方法，利用离散流体区域形成动网格系统，计算得出管道波浪力，随管道与海底的距离、水深和波高关系。贾宏伟[10]建立二维波流数值水槽，对海底管道受力进行了波流力数值模拟计算，得到管道各方向的受力过程和受力波动频率。

结合前期所开展的越南沿海电厂二期工程取排水玻璃钢管受力物理模型试验研究成果，对不同介质内玻璃钢管受波浪力，利用Fluent软件中的VOF模型(对波浪自由表面进行捕捉)开展了数值模拟研究，并结合对比物理模型试验的结果，进一步分析不同介质内玻璃钢管波浪力变化规律，为电厂玻璃钢管的工程设计、管道铺设提供依据。

1 数学模型的建立与验证

1.1 控制方程

采用以速度和压力为变量的不可压缩黏性流体的N-S方程组，表达式如下

连续方程

(1)

动量方程

(2)

(3)

式中：u和v分别为x、y方向的速度分量；g为重力加速度；ρ为流体密度；p为压强；μ为动力黏性系数；Sx和Sy分别为x、y两个方向的附加动量源项。

1.2 数值水槽造波与消波方程

水槽采用边界源项造波法，综合考虑重力和粘性效应两因素的共同影响，生成有限振幅Stokes波，对于Stokes波的速度势可展开为关于波陡的幂级数形式，且级数越高对波型刻画越为精细，计算越为复杂，综合考虑工作需求和计算成本，本文选取二阶Stokes波作为目标波型，根据造波理论[11]，波面过程计算表达式如下

(4)

(5)

式中：A为波浪振幅；k为波数；h为水深；S为造波板的位移；t为时间；ω为圆频率；其他字母含义同上。

水槽端部采用阻尼消波的方式，即在消波段区域添加动量方程阻尼源项使波浪在阻尼层内衰减，主要表达式如下

(6)

(7)

式中：ρ为水体密度；p为水体压强；μ为消波系数，为使波浪平缓过渡，μ随x由0递增，即

μ=a(x-x0)

(8)

式中：a为常数，按照工程计算实际经验取值为1.0～50.0；x0为消波区起始位置水平坐标值，其他字母含义同上。

1.3 模型网格及边界设置

为与物理模型试验结果进行对比，数值水槽模型设置与断面物理模型试验相同，同样采用了λ=1:20的模型试验比尺，设置数值水槽高0.2 m，长20 m，研究玻璃钢管基槽为梯形状，尺寸为：高0.25 m，底宽0.4 m，顶宽1.4 m，基槽内放置管道直径为0.15 m、管道长度每节为0.8 m，具体见图1。计算采用结构化的四边形网格，为了研究管道的受力情况，对管道附近局部网格进行加密，网格单元尺寸为0.04 m。求解设置中，压力速度耦合选PISO算法；压力方程离散选择Body Force Weighted格式。时间步长Δt取为0.001 s，每个时间步最大迭代20次残差可收敛。

注：尺寸为原型值。图1 数值水槽内模型布置Fig.1 Model layout in numerical flume

1.4 模型验证

为保证模型的准确性，对数值水槽造波的波面过程进行了计算与验证，在波高H=5 cm、周期T=1.4 s、水深d=9 cm和波长L=1.27 m波浪作用条件下，1、5倍波长处数值波形与理论波形的比较，见图2。为验证人工阻尼消波的效果，这里给出了8倍波长处的波高随时间的变化历程(见图 3)，由图可知，所设置的人工阻尼区较好地衰减和吸收了波浪的能量，避免了其在壁面的反射及其对计算区域内部波浪场的干扰，达到了预期的效果。因此所建立的波浪数值水槽可开展不同水深、波高和周期条件下，波浪循环荷载作用的管道受力计算。

2-a 1倍波长处(x/L=1)2-b 5倍波长处(x/L=5)图2 波面时间过程线的数值解与理论解对比Fig.2 Comparison between calculated wave surface process and target value

图3 8倍波长(x/L=8)处波面时间过程线Fig.3 Wave front time history line at 8 times wavelength

表1 计算组次Tab.1 Calculation groups

2 计算成果与分析

2.1 计算组次

与物理模型试验组次相对应，分别选择密度为1 300 kg/m3泥水混合物和清水两种不同介质，通过改变入射波高(0.6 m、0.8 m、1.0 m、1.2 m和1.4 m)、周期(4.5 s、5.4 s、6.3 s、7.2 s、8.0 s)和水深(1.0 m、1.4 m、1.8 m、2.2 m和2.6 m)的方法来研究玻璃钢管所受波浪力变化规律，计算组次见表1。对玻璃钢管受波浪力处理定义为:平行波浪传播方向水平力Fx，垂直波浪传播方向上托力Fz。

2.2 模拟结果及分析

利用率定好的数值水槽，在清水和泥水混合的条件下，分别对表1中不同波高、周期和水深各组次进行了计算，得到不同玻璃钢管受力结果见图4，由图中可得：(1)两种介质中玻璃钢管所受波浪力，其规律大体一致，但在泥水中管道受力总体小于在清水中，分析主要原因是泥水中动力粘度较大导致；(2)玻璃钢管所受波浪力与波高呈正相关关系，与波浪周期呈弱正相关关系，与水深(覆盖层厚度)呈弱负相关关系；(3)玻璃钢管受力均有水平力大于上托力，最大分别约为10.5 kN/m和5.0 kN/m；(4)对比波高、周期和水深影响因素，管道受力受波高的变化敏感性最大，周期次之，水深最小。

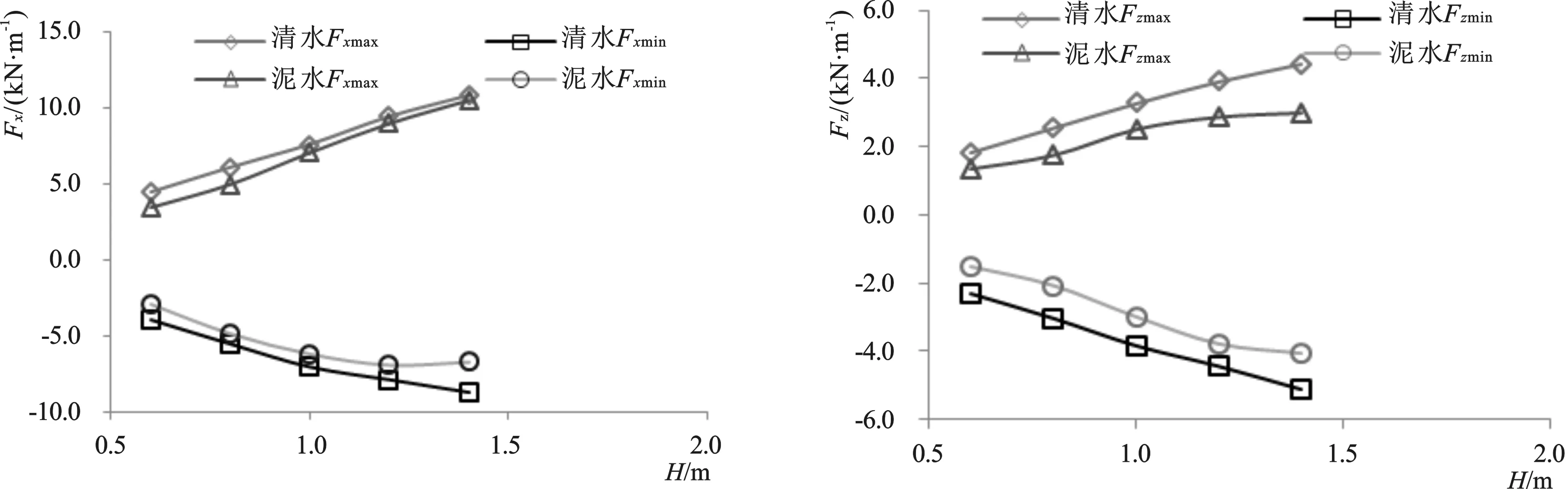
4-a 不同波高(T=6.3 s,d=1.8 m)作用下管道受力结果变化规律

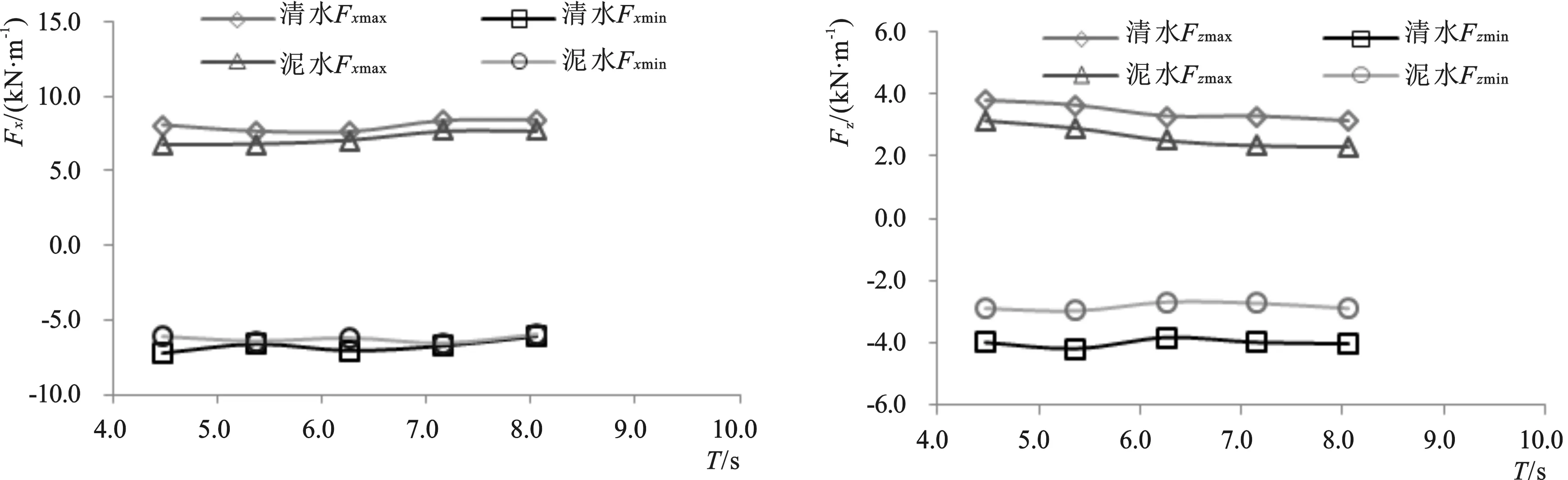
4-b 不同周期(H=1.0 m,d=1.8 m)作用下管道受力结果变化规律

4-c 不同水深(H=1.0 m,T=6.3 s)作用下管道受力结果变化规律图4 不同介质内管道受波浪力结果Fig.4 Results of wave forces on pipes in different media

2.3 与物理模型试验结果对比分析

为进一步论证其规律性，将数值模拟计算的受力结果与物理模型结果进行对比，见图5，由图可知：(1)物模试验中玻璃钢管受力测定存在一定的误差，个别组次玻璃钢管受力互有增减，但差别不大，玻璃钢管受波浪力，数模与物模试验得到结果规律大体一致，即与波高、周期成正比例关系，与水深成反比例关系；(2)数模得到受波浪力结果均大于物模结果，分析主要原因为在数值模拟时参数设置考虑了液体的运动粘度，而在物理模型试验中，压力传感器只能测到波压力，粘性阻力无法测得，因此对于泥水条件下，受压力传感器本身特点影响，数值模拟结果更为合理。

依据数值模拟计算结果，统计并拟合(见图6)玻璃钢管管道受力与波高H、周期T和水深d的关系如下

(9)

(10)

式中：Fx、Fz分别表示水平力和上托力。

5-a 不同波高(T=6.3 s,d=1.8 m)作用下数模、物模管道受力结果对比

5-b 不同周期(H=1.0 m, d=1.8 m)作用下数模、物模管道受力结果对比

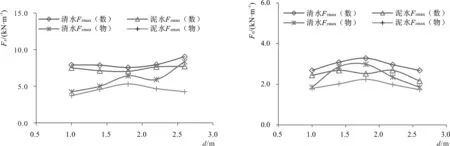
5-c 不同水深(H=1.0 m, T=6.3 s)作用下数模、物模管道受力结果对比图5 数模与物模之间管道受波浪力结果对比Fig.5 Comparison of wave force results of pipeline between digital model and physical model

3 工程适用性分析

通过上述在不同介质下玻璃钢管受力结果可知，随着介质的密度减小，管道的上托力逐渐增加，即当覆盖层土层产生液化时，会存在管道上浮的风险；另外参考本次物理模型试验结果[12]，得到施工期覆盖物在倾倒的过程中，管道产生逐渐上浮并最终稳定在回填物中某一高程，同时在越南某项目现场也出现玻璃钢管上浮拱起现象。因此若覆盖层下沿程管道存在不均匀上浮，则易出现受力不均，产生断裂事故。

对此，针对本次项目，越南沿海海岸地质条件为淤泥质，此时埋设玻璃钢管的基槽中水体含沙量较大，若管道施工过程中未注意而产生上浮，则会影响到玻璃钢管长期运行的稳定性，因此依据研究所得到玻璃钢管上托力的规律和结合现场实际情况，以及考虑管道上浮和材质等因素，对现场玻璃钢管施工，提出加固改善措施的建议，见图7和表2。

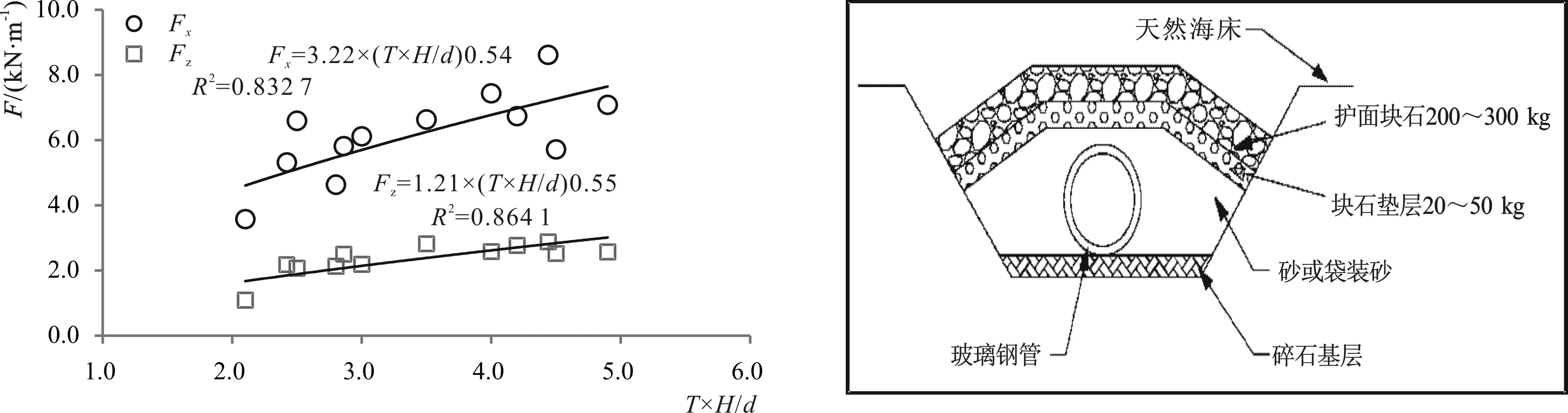
图6 管道受力与H、T、d之间拟合关系Fig.6 Fitting relationship between force and h, t, d图7 回填断面加固示意图Fig.7 Schematic diagram of backfill section reinforcement

4 结语

本文利用Fluent软件建立二维数值水槽模型，对玻璃钢管分别在两种不同介质内受波浪作用，进行了不同组次的受力计算，得出以下结论：

(1)两种介质中玻璃钢管所受波浪力，其规律大体与波高、周期呈正比例关系，与水深呈反比例关系，且在清水条件下大于泥水条件下的受力；管道的水平力一般大于上托力，并且最大分别为10.5 kN/m和5.0 kN/m；管道受力受波高的变化敏感性最大，周期次之，水深则最小，由此拟合得出力与波高、周期和水深三者间公式。

(2)管道受力结果，数模与物模结果对比，两者与每个影响因素之间规律基本一致；数模受力结果均大于物模结果，对于泥水条件下，受压力传感器本身特点影响，采用数值模拟结果更为合理。

(3)根据试验得到管道受力结果，结合现场底质、覆盖层实际情况，以及考虑管道上浮和材质等因素，对现场玻璃钢管的施工提出若干加固措施的建议。