对一道2021年八省市联考题的反思与结论拓展*

湖北省恩施州教育科学研究院(445000) 周 威

一、试题呈现与问题反思

例1(2021年八省市联考数学第21 题) 双曲线= 1(a ＞0,b ＞0) 的左顶点为A, 右焦点为F,动点B在C上.当BF⊥AF时,|BF|=|AF|.

(1)求C的离心率;

(2)若B在第一象限,证明: ∠BFA=2∠BAF.

此题题干简洁,要证明的结论也十分简约,给人第一印象就是“清爽”简单.实际上,本题解题思路开阔,解法也不唯一.第(1)问答案为离心率e=2;第(2)问对学生来说入手容易,重点考查化归转化思想,考查学生对“斜率”与“倾斜角”的转换关系, 通过正切的倍角公式证明角与角之间的关系,落脚于考查学生逻辑推理、直观想象素养,与传统的“直线代入圆锥曲线方程”数学运算有一定的区别,从而难度上有所下降.毫无疑问,第(2)问中的关系式∠BFA= 2∠BAF是在离心率e= 2 时才成立,解题过程中要抓住其数学本质即直线BA,BF的特殊斜率关系tan ∠BFA=tan 2∠BAF.

那么,在一般的双曲线中,甚至在一般的圆锥曲线中,直线BA,BF的斜率关系是怎样的? 数学教师若能从这个“一般与特殊”的角度,运用归纳与演绎推理,那么对问题的认识无疑是更深入更全面的.

二、结论拓展

结论1双曲线= 1(a ＞0,b ＞0)的左顶点为A,右焦点为F,动点B在C上,记C的离心率为e,设直线BA的斜率为k1(k1/=0),直线BF斜率为k2(k2/=0),则k2=

证明因为A(-a,0),F(ea,0),设(0＜θ ＜2π,θ /=π),则

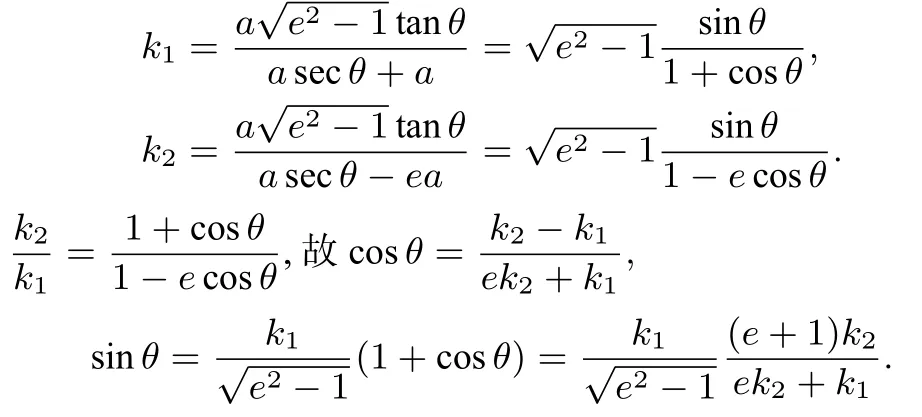
所以

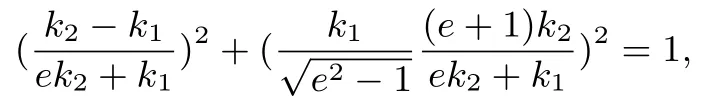
即

化简得

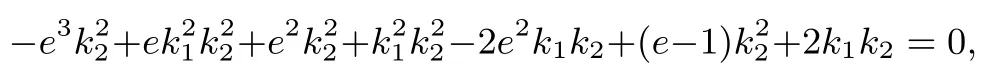
即

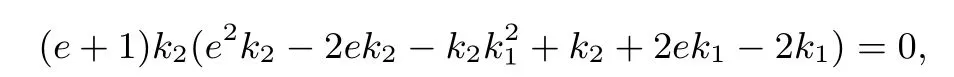
由于k2/=0,化简可得

特别地, 当e= 2 时,k2=而k2=-tan ∠BFA, 从而有例1 中要证明的等式关系.另外, 此结论对椭圆也成立,抛物线情形类似.

结论2椭圆C:= 1(a ＞b ＞0)的左顶点为A,右焦点为F,动点B在C上,记C的离心率为e,设直线BA的斜率为k1(k1/= 0), 直线BF斜率为k2(k2/= 0), 则

证明因为A(-a,0),F(ea,0),设(0＜θ ＜2π,θ /=π),则

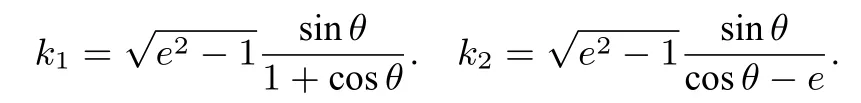
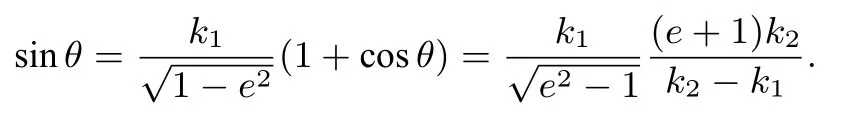
所以

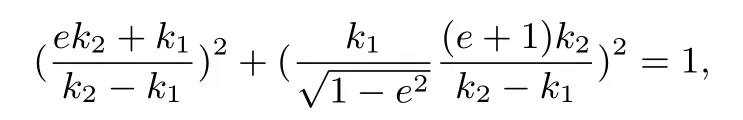
即

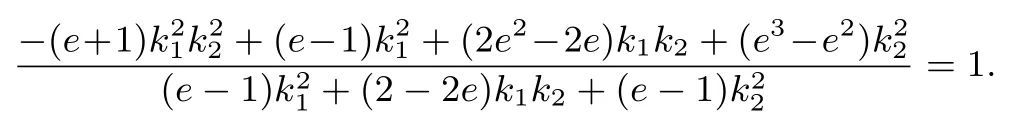
移项有

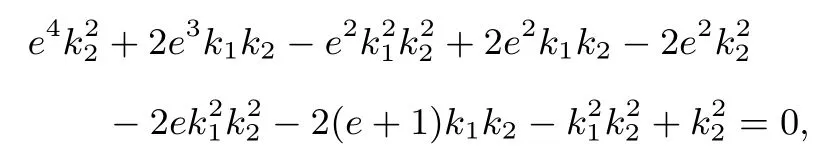
即

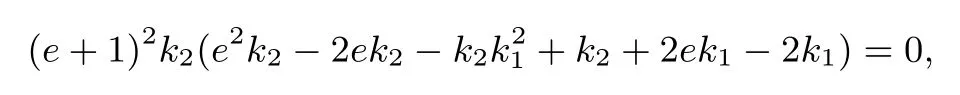
由于k2/=0,化简可得

结论3抛物线C:y2= 2px(p ＞0)的顶点为A,焦点为F,动点B在C上,记直线BA的斜率为k1(k1/= 0),直线BF斜率为k2(k2/=0),则k2=

证明因为A(0,0),设B(2pt2,2pt)(t /= 0),

三、结论的应用举例

例2已知椭圆= 1(a ＞b ＞0)经过点设椭圆左顶点为A,右焦点为F,右准线与x轴交于点M,且F为线段AM的中点.

(1)求椭圆C的标准方程;

(2)若过点A的直线l与椭圆C相交于令一点P(P在x轴上方),直线PF与椭圆C相交于另一点Q,且直线l与OQ垂直,求直线PQ的斜率.

解析(1)

(2) 由(1) 得椭圆离心率e=设直线l斜率为k1(k1＞0), 直线PQ斜率为k2, 则OQ的斜率为由结论2 可得k2=直线OQ方程为y=PQ方程为y=联立可得因为Q在椭圆上,解得k1=从而k2=

点评本题考查椭圆与直线位置关系、直线斜率的求法,当然可以从通性通法的角度将直线代入椭圆方程,利用韦达定理进行求解.而基于探究结论的解答,一定程度上体现数学探究在解题教学中的重要性.

例3过椭圆C:= 1(a ＞b ＞0)的左顶点A且斜率为的直线交椭圆C于另一点B,椭圆的右焦点为F,连接BF,设BF的斜率为k,若k ＜-1,则椭圆离心率的取值范围是____.

解析设椭圆离心率为e, 由结论2 可得,k=因为k ＜-1,1-e ＞0,所以

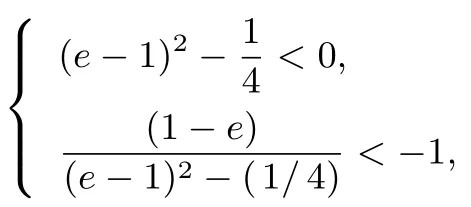
由(e-1)2-得e2-3e+＞0,从而e ＜或e ＞故

点评考查了椭圆与直线的位置关系,基于探究结论,从直线的斜率和椭圆的离心率的关系进行命题创设.

复习备考中很有必要立足基础素材,从试题隐性要素的角度抓住数学问题本质,实现对试题知识点的拓展、发散,以及对相关知识点的重组和整合,基于教材和高考导向进行试题改编,引导学生发现、提出问题,试图让学生抓住同类数学问题的本质.