例谈“微建模”问题的设计
华南师范大学附属中学(510630) 周建锋
问题是数学的心脏,许多数学规律的发现都是人们在不断提出新问题的过程中得到的.我们在指导学生学习数学的时候也要鼓励学生善于提出问题,研究问题,才能进一步提升数学能力,培养探索真理的精神.而情境问题最能展示实际问题的情形,实现数学应用于实践的效能.
问题情境是指针对某个有待完成的任务,要由某个人或某群人加以联结、整合的一组背景化信息,这个任务的结果如何事先并不是一目了然的.确定问题情境的构成部分有两个: 一方面是情境,它带来的主要就是一个主体和一个背景;另一方面是问题,它主要通过一个障碍、一个有待完成的任务、一些要联结起来的信息来定义.
与传统的应用题比较,情境问题主要体现真实的问题情境,所提供的条件往往是“不良结构”,即不如传统应用题中所有条件都已进行“优化”, 条件的明确性和指向性都比较强.真实的情境问题中,问题解决者首先要对条件进行梳理,进行合理化假设,从而有利于构建相应的数学模型.笔者曾与华南师范大学数学科学学院冯伟贞副教授进行过交流,把这类介于数学建模与传统应用题之间的问题定义为“微建模”问题.
对于“微建模”问题的设计,第一步在于构建真实的问题情境,而构建问题情境,一方面可以直接取材于现实生活中的情境问题;另一方面可以从现有的一些应用题出发,去除“加工”后的条件,还原真实、合理的问题情境.
第二步就在于设计目标问题,即需要解决的目标是什么.同一个问题情境可以设计出多个不同的目标问题,目标问题的设计可以多结合生活中的优化问题,如面积最大、容量最大、用料最省、利润最大等.
下面通过一个实例展示“微建模”问题的设计过程.
人教A 版必修4 第3 章有这样一道应用题: 在半径为1,圆心角为60°的扇形铁皮上裁剪一块矩形铁皮,使矩形的一条边置于扇形半径上.问如何裁剪使得矩形铁皮面积最大?
这是一道比较优化了的应用题,数据清楚,裁法明确,基本上只需要设出变量,建立函数关系,即可求解.但这样的数学问题隐去了问题探索的过程,把它与现实生活中的实际情境割裂开来.
一、还原问题情境
设计情境问题: 张师傅手里有一块扇形的铁板(圆心角不大于直角),需要从中裁剪出一块矩形铁板,请你帮张师傅设计裁剪的方法,使得裁剪出的矩形铁板面积最大.
二、问题的探索
首先可以考虑有哪些易于操作的裁法,容易想到的裁法有如下两种(图1、图2 分别记为裁法一、裁法二):
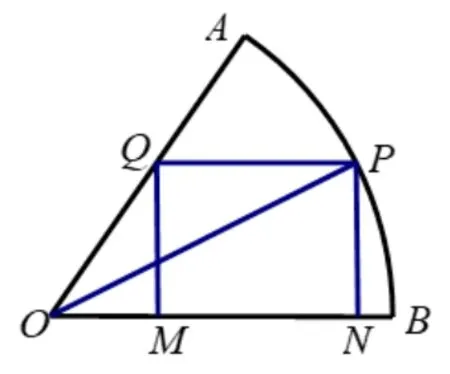
图1
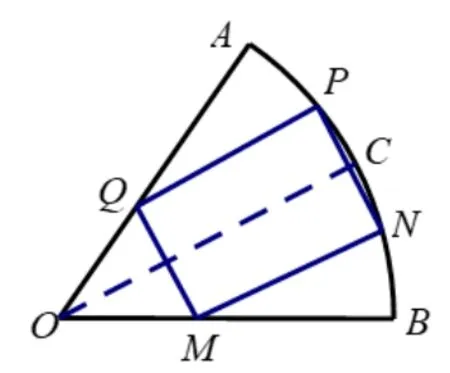
图2
不妨设扇形半径为1.当圆心角α≤时, 在裁法一中, 如图1, 设∠AOB=α, ∠POB=θ(0<θ <α), 则PN=sinθ,MN=ON -OM=cosθ-cotαsinθ,
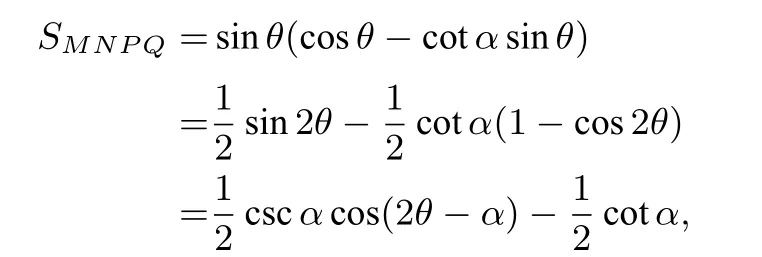
注意到裁法二中,沿∠AOB的角平分线OC裁开,由对称性,每一部分均为裁法一中的情境,易得裁法二得到的矩形面积为所以0<<1),故当α≤时,裁法一均比裁法二得到的矩形面积更大.其次,以上两种裁法位置都比较特殊,那更一般的裁法会如何呢? 会不会有比前两种更优的裁法?
裁法三: 更一般的裁法,如图3,假设MQ是定长,分别过M、Q作MQ的垂线,交扇形弧长于N、P.不妨设MN≤PQ,设MQ=a,∠QMO=由对称性,不妨设, 则以O为原点,OB为x轴建立直角坐标系,则MN:y= cotθ(x-),代入x2+y2= 1得:cos2θ= 0,yN=则
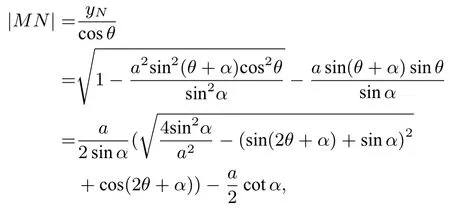
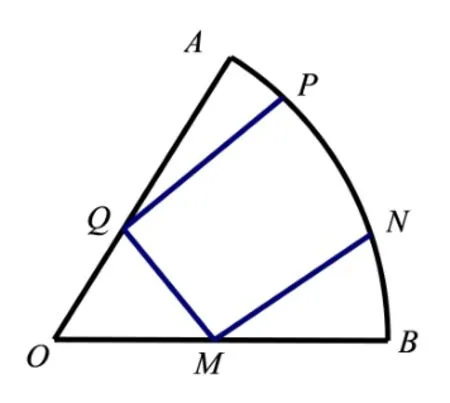
图3
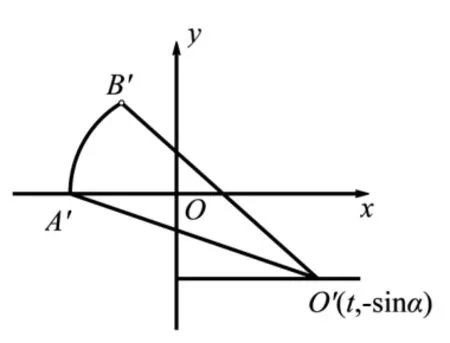
图4
设
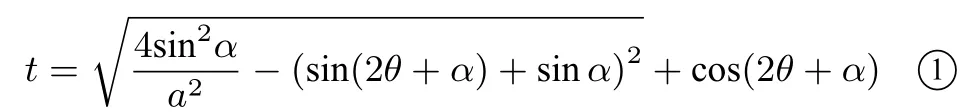
只需求t在时的最大值.设x= cos(2θ+α),y= sin(2θ+α), 则圆弧C:x2+y2= 1(-1 ≤x≤-cosα,0 ≤y≤sinα), ①式即为:(x-t)2+(y+sinα)2=是以O′(t,-sinα) 为圆心,为半径的圆.
如图4,t最大当且仅当O到O′的距离最大, 即O′在A′B′中垂线右端且圆O′与圆弧C只有公共点B′时,t最大.此时θ=即裁法一得到的矩形铁板面积最大.最后可以让张师傅这样裁剪:
1.先作出圆心角的平分线与圆弧交于一点P;
2.再由P点向扇形其中一条半径作垂线(得到垂足点N),同时过P点作该半径的平行线,与另一条半径交于一点Q;
3.继续由Q点作第一条半径的垂线,得到垂足点M.
以上得到了四个点M,N,P,Q即为要得到的矩形的四个顶点,裁剪工作完成(如图1).
三、问题的进一步设计
不满足于只求面积的最大值,再设计问题: 在裁法一或裁法二中,为了充分利用剩下的边角料,在剩下的边角料中再裁出一个圆形铁板,加上刚才裁出的矩形,做成一个无盖的圆柱形铁桶.那又该如何裁剪, 使得到的铁桶容积最大?(不考虑损耗且只计算α=时的情形)
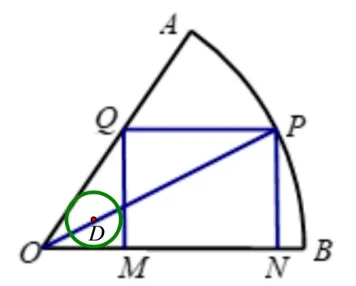
图5
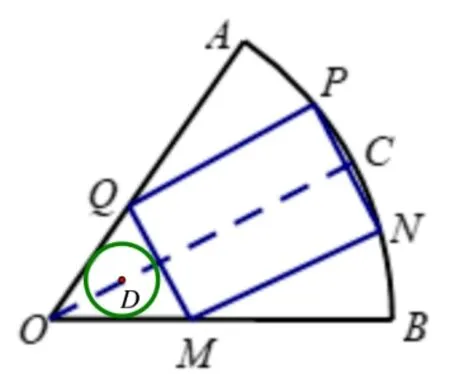
图6
问题的探索考虑裁法一和裁法二,问题关键在于能否在边角料中裁出圆形铁板, 使其周长不小于矩形的一条边,这样就可以依据其中一边的周长去裁出需要的圆形铁板.在裁法一中,矩形一边PN=另一边MN=先尝试在边角料OMQ中裁一个内切圆(如图5),设其半径为r,RtΔOMQ中,OM=由等面积法易得:r=此内切圆的周长所以能裁出一个圆形铁板(把内切圆适当缩小),以MNPQ为侧面组合成圆柱体.以MN为底面周长时容积V1=以PN为底面周长时容积V2=所以在裁法一中可以组合出以MN为底面周长的圆柱形铁桶,容积为
在裁法二中,矩形的边MN=PN=.在等边三角形OMQ中(如图6),边长为所以其内切圆半径,内切圆周长所以能裁出以为周长的圆形铁板, 这样得到的圆柱形铁桶体积V3=最终,在裁法一中利用剩下的边角料,可以裁出一个圆形铁板,和矩形铁板组合成圆柱形铁桶,最大容积为
其实这个问题情境还可以进一步的设计,如组合出长方体无盖铁桶,又该如何设计? 留给读者去思考.通过创设真实、合理的情境问题,在不断的探索中寻求问题的真相.这样不仅有利于更深入地解决问题,也有助于提升学生运用数学解决问题的能力.同时,作为教师在这个过程中,不仅为学生的成长创造了条件,也享受了创作的乐趣.

