例谈“定比点差法”在解析几何问题中的应用
安徽省芜湖市第一中学(241000) 刘海涛
1 问题的提出
在处理解析几何“中点弦”问题时, 我们常用的方法是“点差法”,该法模式化强,计算量小,学生易于掌握,其实在面临“非中点弦”问题时,我们依然可以使用“点差法”,只是在处理非中点问题时,需要根据线段所分得的比值做代数处理,一般把这种方法叫做“定比点差法”,文[1]以椭圆为例给出了该法的简单介绍,并在两道圆的问题和两道椭圆的问题中给出了该法的运用,笔者认为介绍的不够全面系统,本文在定比分点的基础上,分别以椭圆、双曲线、抛物线为例介绍该法的由来,并例举该法在7 类解几问题中的应用,全面系统地介绍了“定比点差法”,现与读者分享交流.
2 “定比点差法”的介绍
2.1 定比分点的定义
若点A(x1,y1),B(x2,y2),P(x0,y0),则x0=
2.2 “定比点差法”的由来
(1)若点A(x1,y1),B(x2,y2)在椭圆=1(a >b >0)上,且点P(x0,y0)满足则
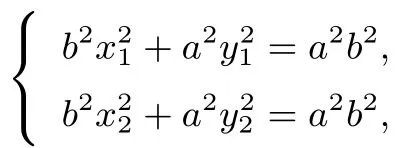
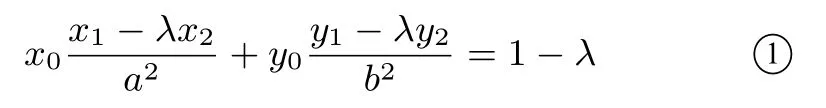
(2)若点A(x1,y1),B(x2,y2)在双曲线=1(a,b >0)上,且点P(x0,y0)满足则
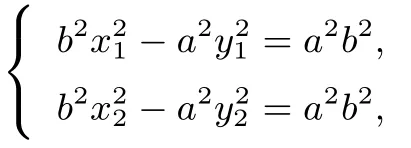
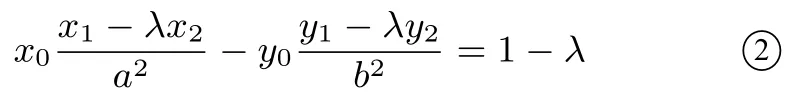
(3)若点A(x1,y1),B(x2,y2)在抛物线y2=2px(p >0)上, 且点P(x0,y0) 满足则于是有= 2p(x1-λ2x2, 整理得即
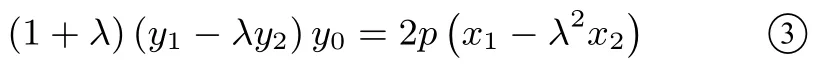
上述表达式①、②、③的推导方法就叫“定比点差法”,由推导过程可以看出, 该法是“点差法”的更一般的推广而已,当λ=1 时“定比点差法”即为“点差法”.
3 “定比点差法”的应用
3.1 应用“定比点差法”求点的坐标
例1已知F1,F2分别是椭圆+y2= 1 的左右焦点, 点A,B在椭圆上, 且则点A的坐标是____.
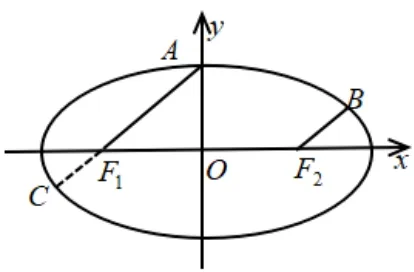
图1
解析如图1, 延长AF1交椭圆于点C, 由对称性得设A(x1,y1),C(x2,y2), 则又所以由点A,C在椭圆上, 则于是有(x1+5x2)(x1-5x2)+3(y1+5y2)(y1- yx2) =-72, 即=-72, 则x1-5x2=联立x1+ 5x2=得x1= 0, 则A(0,±1).
评注由向量数乘的几何意义知F1A//F2B且|F1A|=5|F2B|,考虑到椭圆的中心对称性,可以延长AF1交椭圆于点C,得到|F1C|=|F2B|,从而得到A,F2,C三点共线,且于是定点F1为焦点弦AC的定比分点,自然想到使用定比点差法.
3.2 应用“定比点差法”求离心率
例2已知椭圆=1(a >b >0),过其左焦点F且斜率为的直线与椭圆交于A,B两点,若求椭圆的离心率.
解析设A(x1,y1),B(x2,y2), 由得由F(-c,0)得
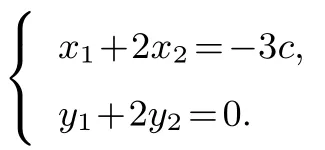
由点A,B在椭圆上,则故有b2(x1+2x2)(x1-2x2)+a2(y1+2y2)(y1-2x2)=-3a2b2,即-3cb2(x1-2x2) =-3a2b2, 则x1-2x2=联立x1+2x2=-3c,得x1==所以于是有整理得4a4-13a2c2+9c4=0,则9e4-13e2+4=0,解得或1,又0<e <1,所以
评注处理焦点弦问题时,相较于联立直线与曲线方程法,定比点差法运算量小,过程简洁.
3.3 应用“定比点差法”求直线方程
例3已知椭圆= 1(a >b >0)的左、右焦点分别为F1,F2,焦距为2,过点F2作直线与椭圆C相交于A,B两点,且ΔABF1的周长为
(1)求椭圆C的标准方程; (2)若|AB|= 4|F2A|,求直线AB的方程.
解析(1)+y2=1(过程略).
(2) 由|AB|= 4|F2A|, 得设A(x1,y1),B(x2,y2), 得又F2(1,0), 所以由点A,B在椭圆上, 则于是有(3x1+x2)(3x1-x2)+2(3y1+y2)(3y1-x2) = 16,即4(3x1-x2) = 16,则3x1-x2= 4,联立3x1+x2= 4, 得x1== 18, 则则kAF2=±1,故lAB:y=x-1或y=-x+1.
评注由平面向量共线定理及向量数乘的几何意义,得自然考虑定比点差法.
3.4 应用“定比点差法”求弦长
例4已知斜率为的直线l与抛物线y2= 3x的交于A,B两点,与x轴交于点P,若求|AB|.
解析设A(x1,y1),B(x2,y2),P(x0,0)(x0>0),由得则由点A,B在抛物线上, 则于是有(y1+3y2)(y1-3y2)=3(x1-9x2),则x1-9x2= 0, 联立x1+ 3x2= 4x0, 得x1= 3x0, 又则y1= 3x0, 由y21= 3x1, 得9x20= 9x0,即x0= 1, 则|AP|=故
评注由知该题可使用定比点差法,得到点A横坐标x1= 3x0,再利用kAP=得到y1= 3x0,利用抛物线方程得到x0= 1,求出|AP|,最后由|AB|=得出答案.
3.5 应用“定比点差法”求定值问题
例5已知过点Q(0,1)的直线与双曲线-y2=1 交于A,B两点,与x轴交于点P,若求证λ+µ为定值.
解析设P(x0,0),由得
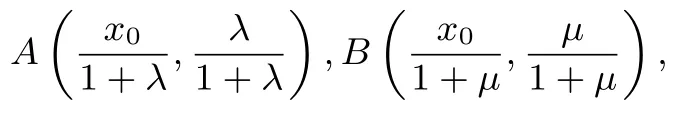
由点A,B在双曲线上,则
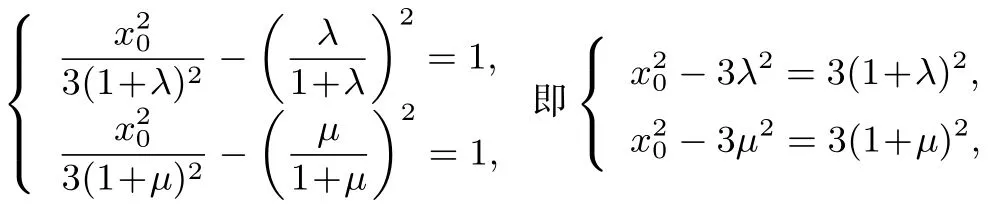
两式相减得λ+µ=1.
评注利用得到A,B两点的坐标,代入双曲线方程,变形做差得到λ+µ= 1,是定比点差的变形应用.另外,该题可以拓展到一般性,有如下结论:
结论1已知过点Q(0,m)的直线与双曲线1(a,b >0)交于A,B两点,与x轴交于点P,若则λ+µ=
由于圆、椭圆、双曲线、抛物线都是二次曲线,很多时候它们之间存在类似的性质,于是类比联想,推广得如下结论:
结论2已知过点Q(0,m) 的直线与椭圆1(a > b >0) 交于A,B两点, 与x轴交于点P, 若
结论3已知过点Q(0,m)的直线与圆x2+y2=r2交于A,B两点,与x轴交于点P,若则
结论1,2,3 的证明,参照例5.
结论4已知抛物线x2=2py上A,B两点,若直线AB分别与x,y轴交于点P,Q,且则λ+µ=-1.
证明设P(x0,0),Q(0,y0), 由得由点A,B在抛物线上,则
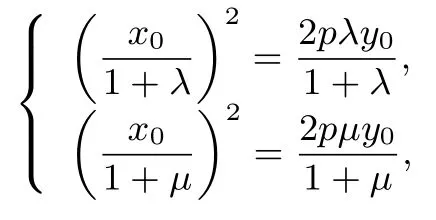
即
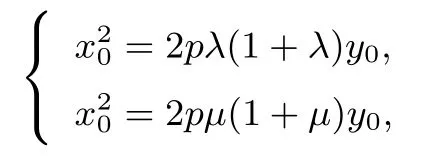
两式相减得λ+µ=-1.
结论5已知抛物线y2=2px上A,B两点,若直线AB分别与x,y轴交于点P,Q,若则
结论5 的证明,参照结论4.
3.6 应用“定比点差法”求定值问题
例6已知过点P(6,0)的直线与椭圆+y2=1 交于A,B两点,C为点A关于x轴的对称点,求证: 直线BC过定点.
解析设A(x1,y1),B(x2,y2), 直线BC与x轴交于点Q(x0,0), 由题知C(x1,-y1), 由向量的共线定理, 设得
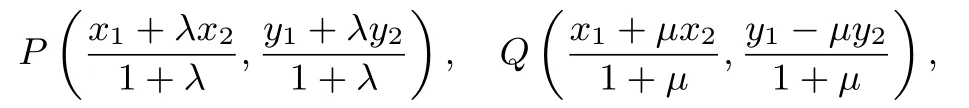
于是有
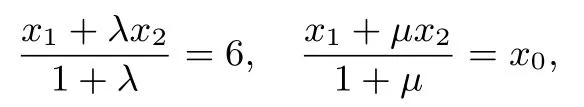
y1+λy2=y1-µy2=0,则λ=-µ,=x0.由点A,B在椭圆上,则
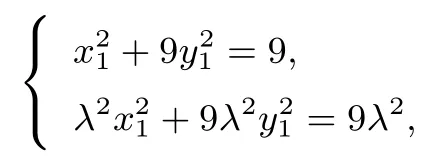
于是有
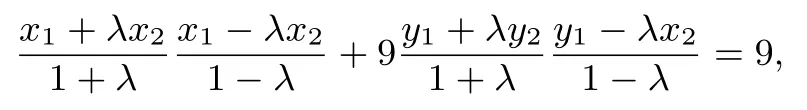
即6x0=9,得故直线BC过定点
评注由对称性,易知直线BC所过定点在x轴上,设所求定点为Q(x0,0), 注意到题中有两组三点共线, 故设接着使用定比点差法解题.
3.7 应用“定比点差法”求定直线问题
例7已知过点P(4,1)的动直线与椭圆交于A,B两点,若线段AB上一点Q满足求证: 点Q总在某条定直线上.
解析设A(x1,y1),B(x2,y2),Q(x0,y0),,则
于是有
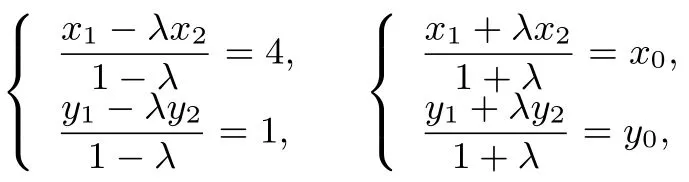
由点A,B在椭圆上,则
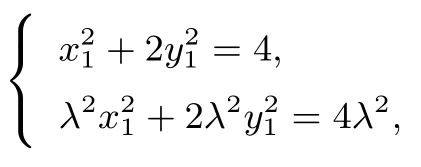
于是有
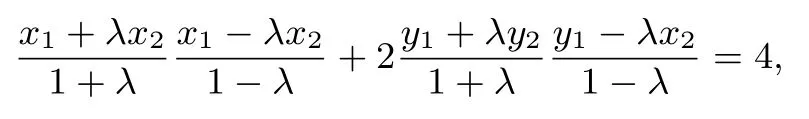
即4x0+2y0=4,故点Q在直线2x+y-2=0 上.
评注该题改编自2008年高考安徽理科卷,共线的四点成两组等比例线段,于是设自然想到定比点差法,非常巧妙地得到结论,体现出定比点差法比其他方法的优越性.
4 总结反思
4.1 方法总结
“定比点差法”属于技巧,并不是解析几何的通解通法,其适用范围较窄,从上述例题的解答过程可以看出,当遇到三点共线、定点、成比例等条件时,我们可以尝试该法.
4.2 解后反思
本文介绍的“定比点差法”,为今后解决一类解几问题提供了新的思路,相较于联立直线与曲线方程的通法,该法过程简洁、计算量小,可以提高解题效率,但是该法有其局限性,我们在日常的学习中,要结合自身掌握程度和实际情况,选择最佳的解题方法,不能盲目追求某一种解法,要学会从不同的解法中汲取不同的数学思想,从而提高自身的数学核心素养[2].

