组合结构发电塔架灌浆连接段接触压分析*

毕继红 谢宇航 赵云 霍琳颖

1.天津大学建筑工程学院 300350

2.滨海土木工程结构与安全教育部重点实验室（天津大学） 300072

引言

近年来我国的可再生能源发展迅速，风力发电装机容量逐年提高，对风电塔的高度和性能也提出了更高的要求。目前我国风机主要采用钢制塔筒结构体系，但对于高度超过100m的风电塔，采用纯钢制塔架存在钢材消耗大、运输施工复杂等问题［1］。因此下部采用预制或现浇筑混凝土塔筒来代替部分钢制塔筒的组合结构塔架逐渐成为超高风力发电塔的主流。由于钢结构塔架和钢筋混凝土基础相连接的部位易产生应力集中现象，在遭遇台风时塔架的破坏位置多数发生在连接段基底［2］，因此连接段的设计至关重要。

灌浆套筒连接结构一般为外侧钢管、内侧钢管以及中间的灌浆组成的统一整体，目前主要应用于海洋结构中。相比传统的连接方式，灌浆套筒连接具有容易控制误差、减少构件疲劳破坏、可以防止水对钢管的侵蚀等优点［3］，但在陆上风电塔中的应用和研究都很少，缺乏相应的理论指导。对于灌浆套管连接段，钢制塔架所受的荷载主要通过压力传递给基础部分［4］，因此，对于塔架的连接段接触压进行分析具有重要的理论意义和工程价值。

目前单桩风电灌浆套管设计规范主要有美国石油协会（API）规范［5］、英国健康与安全执行局（HSE）规范［6］和挪威船级社（DNV GL）规范［7］。现有规范对于这种新型灌浆结合部设计并不能完全适用，存在以下问题：（1）对大直径灌浆套管、高强灌浆材料的研究并不充分。API 规范及HSE规范主要基于早期的中低强度水泥材料灌浆套管试验，且试验试件直径均小于80cm，对于大直径灌浆套管并不可靠；（2）现有规范主要适用于海上风电单桩基础。灌浆连接较少应用于陆上组合结构风电塔结合部，其相比海洋结构多了外侧混凝土部分，而现有研究均未考虑外侧混凝土对灌浆连接段受力的影响。综上有必要对该结构灌浆连接段进行有限元及理论分析。

本文充分考虑材料特性，使用有限元软件ABAQUS建立了150m 高组合结构塔架模型，重点分析了灌浆连接段受力，并与传统的灌浆连接接触压分布公式结果对比，得到了该新型结构的接触压分布规律；最后推导了该结构在外力作用下的最大平均接触压公式，为工程实际提供了理论参考。

1 灌浆连接方案及受力特点

本文基于德国2018 年盖尔多夫风电-抽水蓄能发电组合结构为建模背景［8］，该项目采用了灌浆连接以改善连接部位的受力性能。结构形式如图1 所示，相比传统海洋结构灌浆套管结构，该结构增加了外侧混凝土部分，通过灌浆套管连接段将上部钢制塔段和下部混凝土塔段连接成整体，并将上部钢塔段传递下来的轴力、剪力、弯矩均匀地传递到下部混凝土塔段。

组合结构塔架采用灌浆连接段的主要目的是将上部钢筒所受的荷载从过渡段均匀传递到桩体。弯矩、轴力及扭矩都主要通过机械咬合、摩擦及接触压传递。机械咬合主要是由于部件表面不平整产生，在设计中通常不考虑［7］；摩擦力在传递荷载的过程中所起到的作用直接与接触压大小有关，因此对连接段的接触压大小进行评估是十分重要的，是判断塔架发生破坏的重要标准。

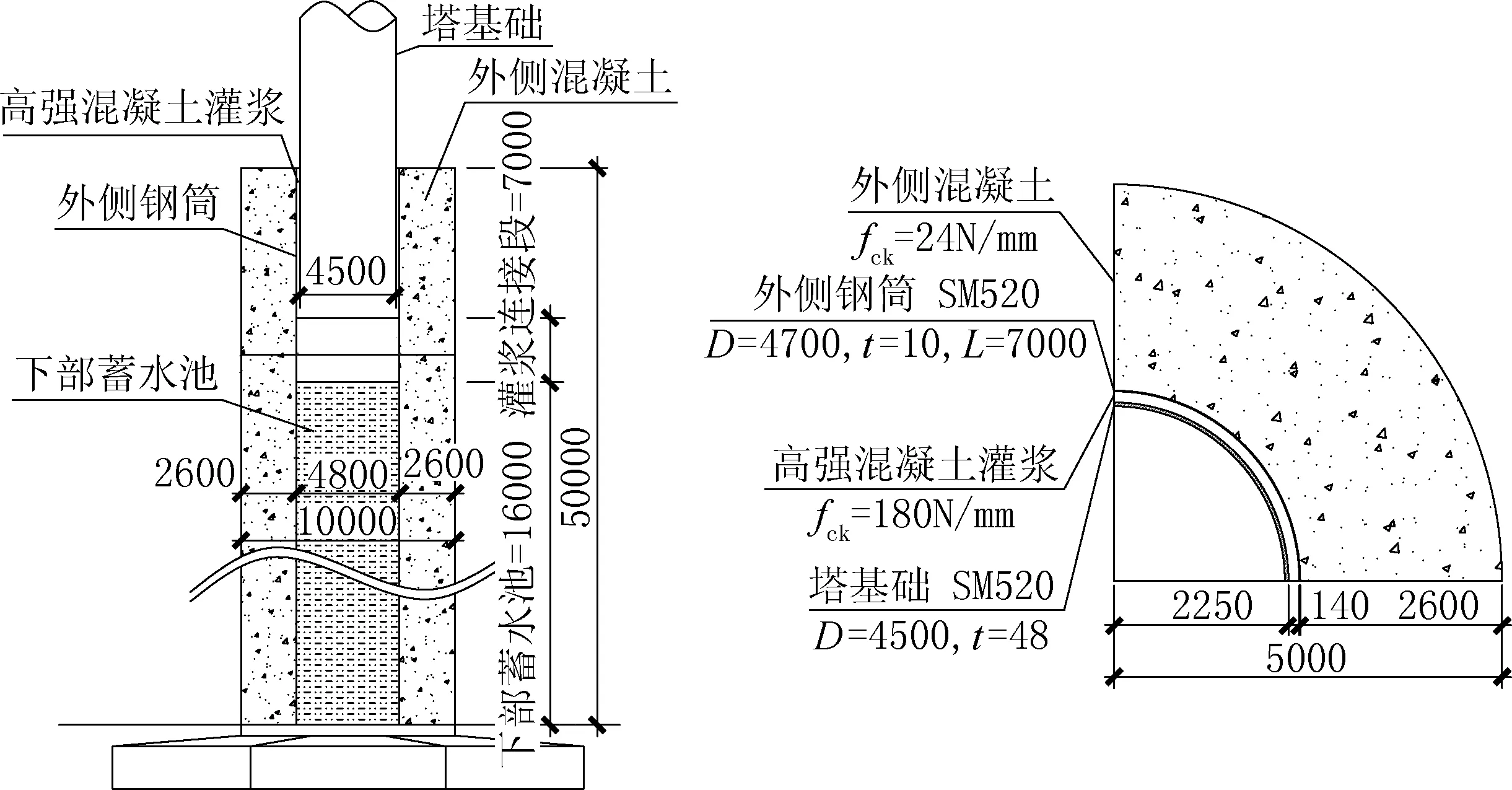
图1 组合塔筒灌浆连接段示意Fig.1 Schematic diagram of grouted connection section of hybrid tower

2 有限元数值分析

2.1 有限元模型建立

1.几何模型及网格划分

本节算例中，模型总高度57.0m。其中：外侧混凝土基础高50m，厚度tc＝2.6m；外侧钢筒长L ＝7m，半径Rtp＝2.4m，厚度ts＝0.01m；高强灌浆混凝土段长L ＝7m，厚度tg＝0.14m；钢塔段长14m，厚度tp＝0.048m。

本文采用有限元分析软件ABAQUS进行建模分析。钢塔段及外侧钢筒是钢管材料，采用ABAQUS四节点缩减积分壳单元S4R来模拟。外侧混凝土及连接处的灌浆材料采用八节点线性缩减积分实体单元C3D8R来模拟。

由于结构形状及荷载的对称性，建立半模型以提高计算效率。划分网格时，按照DNV 规范推荐，将灌浆部件沿厚度方向分为3 份，与钢塔、灌浆及外侧钢筒相比，外侧混凝土体积较大，在外侧采用较大尺寸单元以减少网格数。高度方向，考虑连接段端部的应力集中现象，在连接段上下应力集中区域内进行网格加密。连接段沿圆周方向划分为60 份，分析模型如图2 所示。

图2 有限元模型示意Fig.2 Schematic diagram of the finite element model

2.本构关系

内侧钢塔段与外侧钢筒使用SM520 钢材，为各向同性线弹性材料，弹性模量Es＝205GPa，泊松比γs＝0.3。灌浆材料为超高强混凝土，按经验取各向同性线弹性本构，弹性模量Eg＝46GPa，泊松比γg＝0.2。外侧混凝土取各向同性线弹性本构，弹性模量Ec＝25GPa，泊松比γc＝0.2。

3.加载方式、约束及相互作用

上部荷载通过钢塔传递至灌浆套管连接段，因此在有限元计算时，在钢塔段顶端施加外荷载。极端荷载情况下，弯矩设计值M ＝151000kN·m，剪力设计值F ＝1900kN，将荷载设计值的一半通过参考点耦合加载在钢塔顶端截面。

基础底面完全固定，约束对称面Y向位移及绕X轴、Z轴的转动。

模型中的相互作用包括外侧钢筒与外侧混凝土、外侧钢筒与灌浆、灌浆与钢塔段三部分。其中外侧钢筒与外侧混凝土设置为绑定约束，其他采用面-面接触。接触对的法向属性均采用ABAQUS中的拉格朗日接触，即“硬接触”。接触面之间只能传递压力不能传递拉力，一旦受拉则两接触面直接分离，支持接触面法线方向的压缩及切线方向的摩擦。

2.2 有限元分析结果

连接段接触压分布如图3 所示，将图中剪力指向的方向定义为0°，灌浆连接段中间位置高度定义为0。从云图中可以看出接触压的分布规律：在弯矩和剪力荷载同时作用下，灌浆部分受到的接触压在上下部分存在明显变化。除边缘应力集中部分，在θ ＝0°处，连接段接触压从上到下逐渐减小；在θ ＝180°处，连接段接触压从上到下逐渐变大。最大接触压出现在云图的右上方和左下方位置。

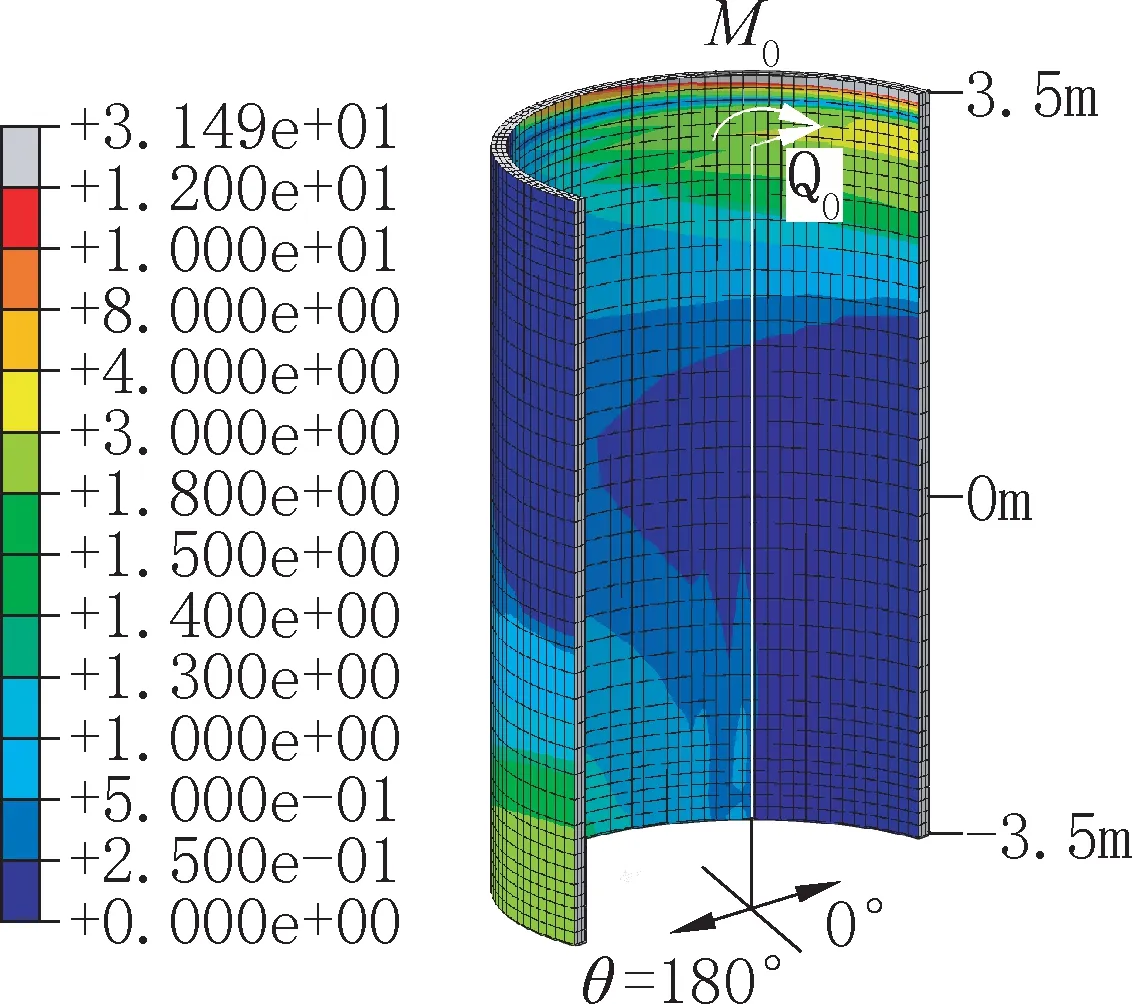
图3 连接段接触压（单位： MPa）Fig.3 The contact pressure of connection（unit：MPa）

3 规范公式结果对比

DNV规范［7］假设灌浆连接段接触压竖向分布如图4 所示，并给出了灌浆连接段最大接触压参考公式：

式中：σ 为最大接触压；L 为灌浆连接段长度；Rp为钢塔外径；μ 为连接段摩擦系数；M0为弯矩荷载。

图5 给出了有限元分析和规范公式分别计算出的灌浆内侧单元接触压沿高度方向的分布结果，其中横轴表示接触压，竖轴表示连接段位置。对比可得：在θ ＝180°处，接触压分布与DNV规范基本相同；在θ ＝0°处，接触压应力集中现象明显，接触压分布范围并非从连接段上端到灌浆连接段中间位置，而是有所减小，与DNV规范假定存在较大差异。DNV 规范公式主要应用于海洋结构，该类型单桩基础结构从外到内分别为外侧钢筒-灌浆-塔基础，并不包含外侧混凝土。推测造成以上差别的原因是由于外侧混凝土存在引起了上部接触压沿高度分布不均。

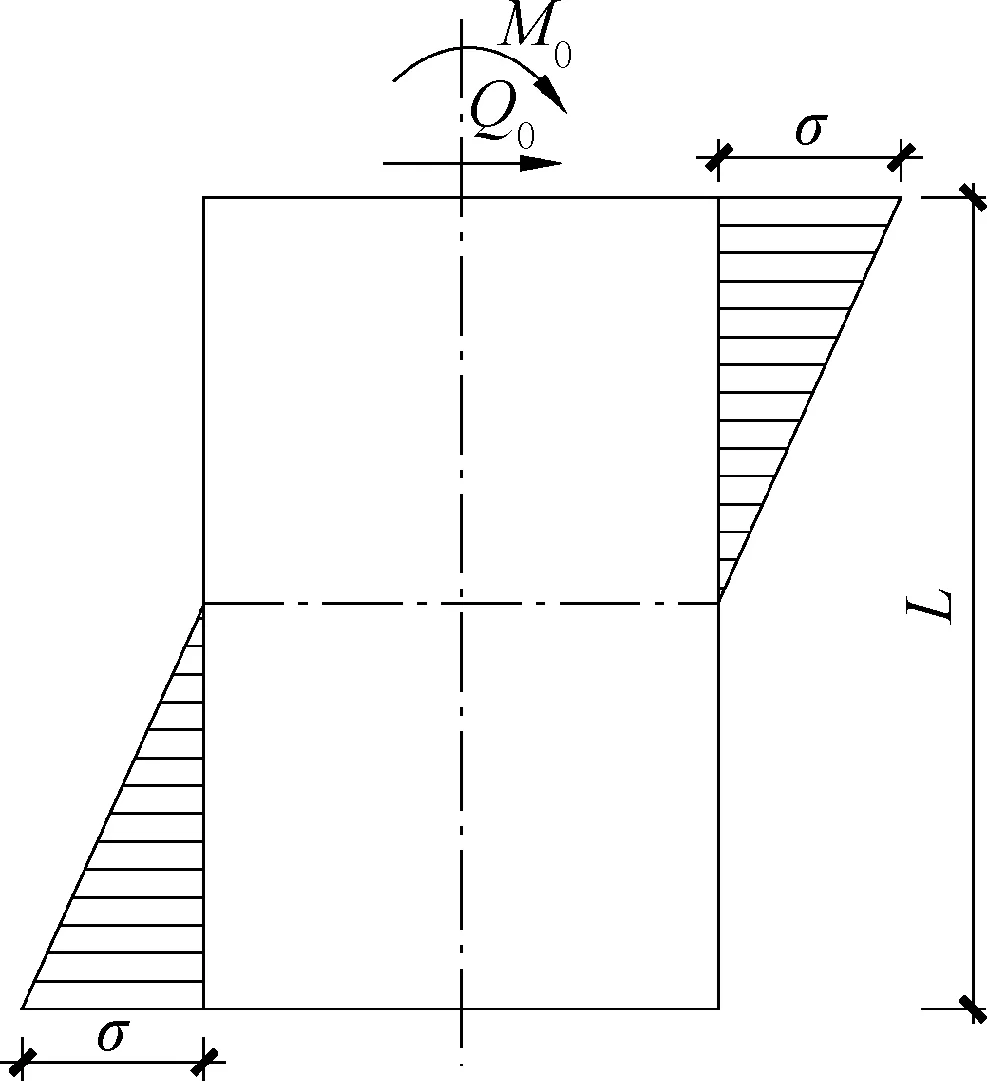
图4 传统灌浆套管结构接触压分布Fig.4 Force state of traditional grouted connection

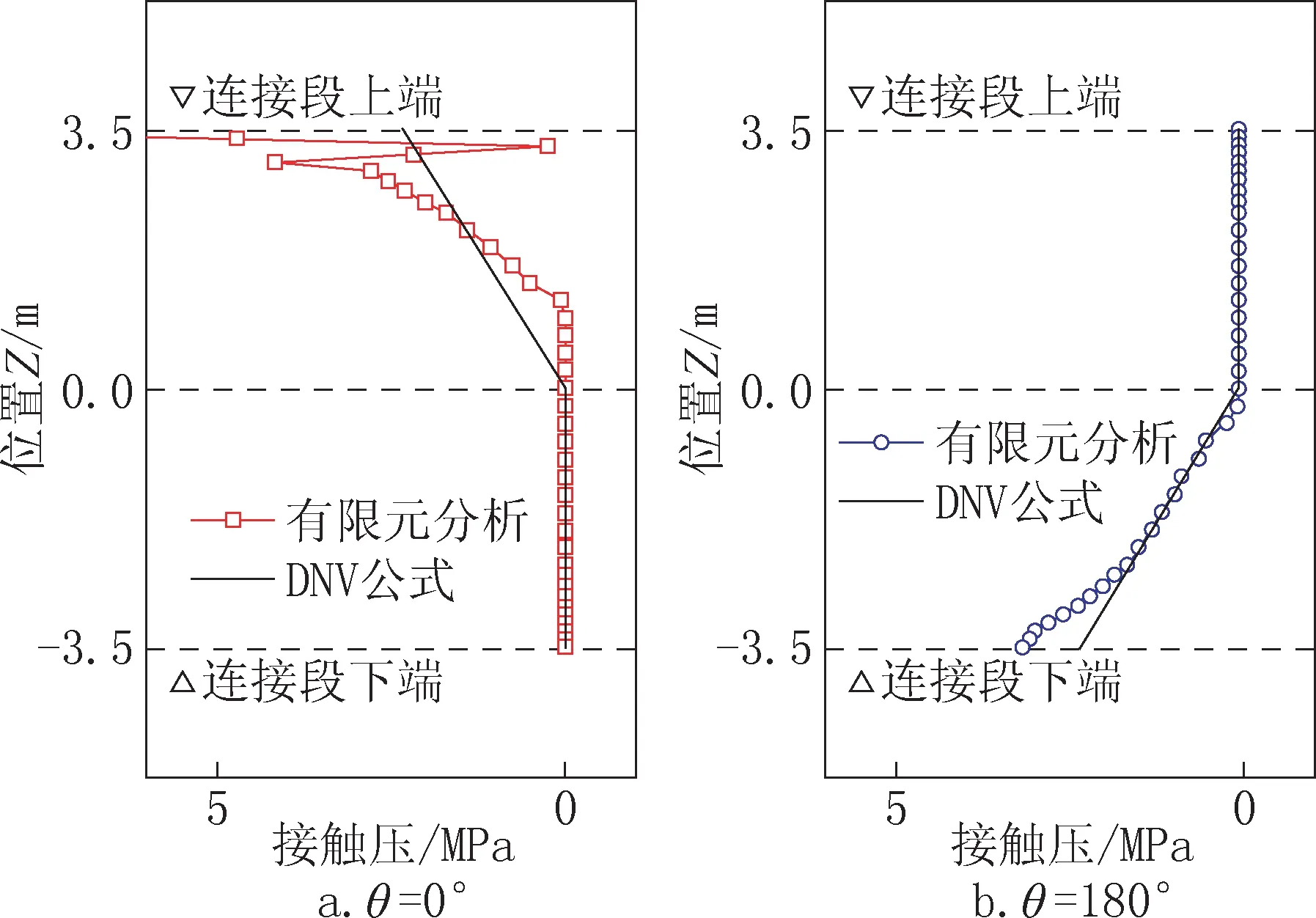
图5 接触压在高度方向上的分布Fig.5 Distribution of contact pressure in the vertical direction

因此，现有规范并不适用于该类新型钢-混组合结构塔筒灌浆连接段受力，需进行理论分析以求得适合该类型灌浆连接段接触压分布的理论公式。

4 理论分析

现有规范中灌浆连接段内力计算理论均基于接触压以中心高度为界，上下均匀分布，如图4所示，但该新型组合结构灌浆连接段接触压沿高度方向分布规律显然与传统假设不同。本节在有限元计算的基础上总结了接触压分布规律，并进一步推导了该结构最大平均接触压公式。

4.1 接触压分布

为进一步研究外侧混凝土厚度对接触压沿高度方向分布的具体影响，以外侧混凝土厚度tc为变量，其他参数不变进行了一系列计算。在第2节有限元模型基础上，通过改变外侧混凝土厚度在tc＝0.3m ～2.6m 范围内建立了11 个计算模型，并通过ABAQUS计算提取了灌浆连接段接触压沿竖向分布结果。分析计算结果可知，下侧受压区接触压分布随外侧混凝土厚度变化不大，除边缘应力集中范围均与图4 下侧接触压分布相同，基本与DNV 规范分布规律一致；而上侧受压区接触压分布范围受外侧混凝土厚度变化影响明显。当外侧混凝土厚度tc不同时，取外侧混凝土厚度分别为0.3m、2.6m 两条接触压曲线为例，上部受压段接触压分布长度L0明显不同，如图6 所示，主要表现为接触压分布高度随外侧混凝土厚度变大而缩短。将数值计算结果L0与外侧混凝土厚度tc进行回归分析，得到公式：

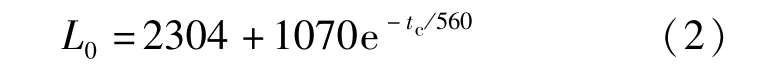
图7 描述了上侧受压段接触压分布范围L0与外侧混凝土厚度tc的关系。由图可知，外侧混凝土厚度由300mm 增加到1600mm 时，接触压分布随外侧混凝土厚度变化很大；外侧混凝土厚度大于1600mm 时，增大厚度对于接触压的分布影响并不明显。

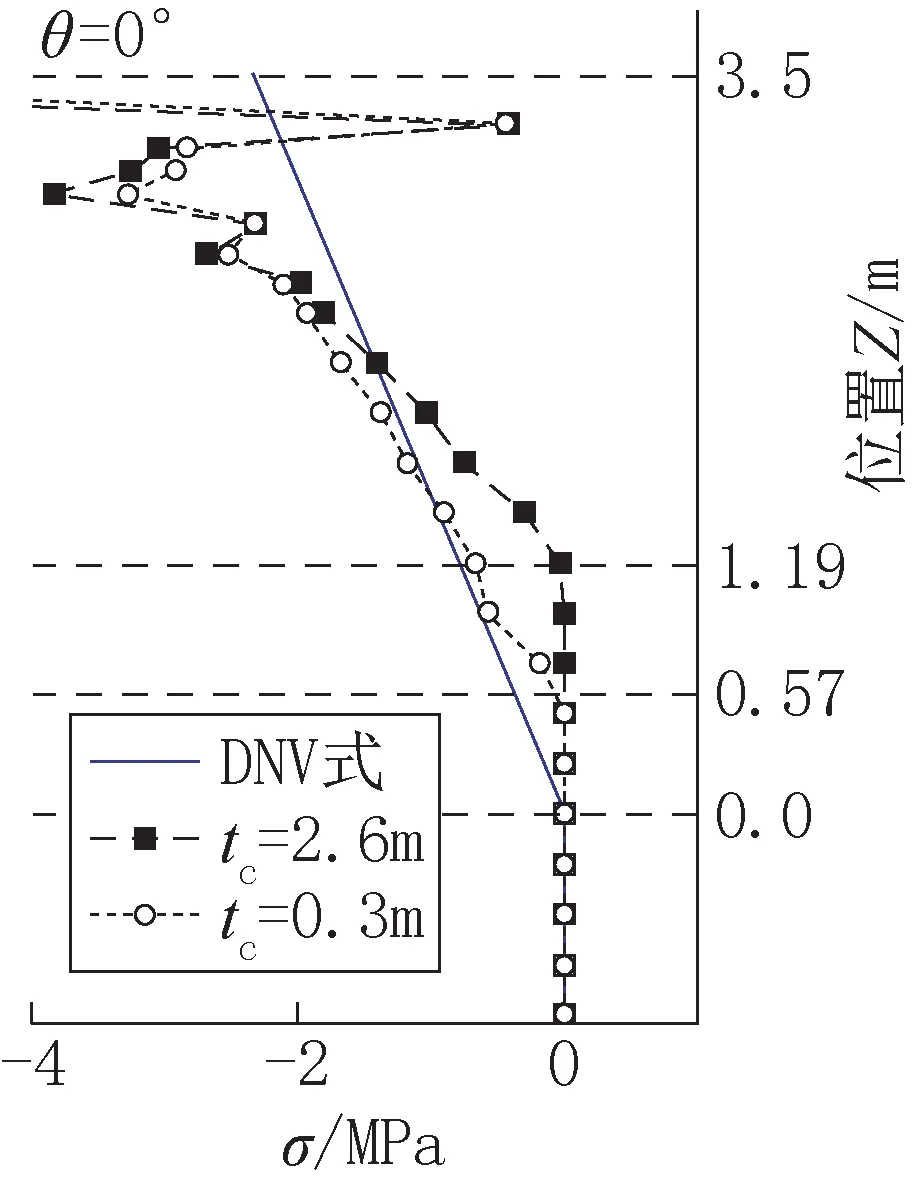
图6 上侧受压段接触压分布对比Fig.6 Distribution of contact pressure on the upper section

图7 上侧接触压分布高度与外侧混凝土厚度关系Fig.7 Relationship between the height of the upper contact pressure distribution and the outer concrete thickness

4.2 最大平均接触压

为了简化计算，主要基于受力平衡、不考虑变形协调，即假定灌浆体非均匀承压时钢管无变形。作用在钢制塔筒上的剪切力Q0和力矩M0主要由连接段的接触压以及接触产生的竖向与水平摩擦力传递给下部结构。钢制塔筒的竖向受力状态如图8，水平向受力状态如图9 所示［9］。此应力状态下，钢制塔筒右侧、左侧受到灌浆压力分别为N1和N2。连接段上、下端的最大平均接触压分别为σ1和σ2。取钢塔连接段最下端截面为受力分析对象，可得到下列等式：

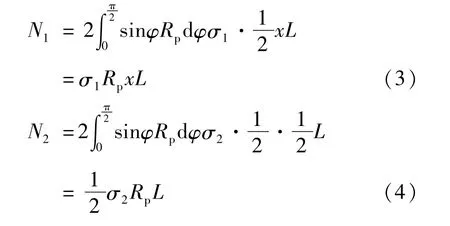
式中：L为灌浆连接段长度；Rp为钢塔外径；σ1为连接段上侧最大平均接触压；σ2为连接段下侧最大平均接触压；x为上侧受压段长度比例系数L0／L。

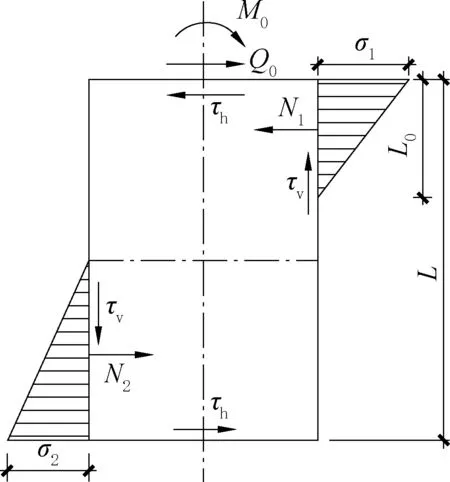
图8 灌浆段钢塔竖向受力状态Fig.8 Vertical force state of steel tower in grouted section

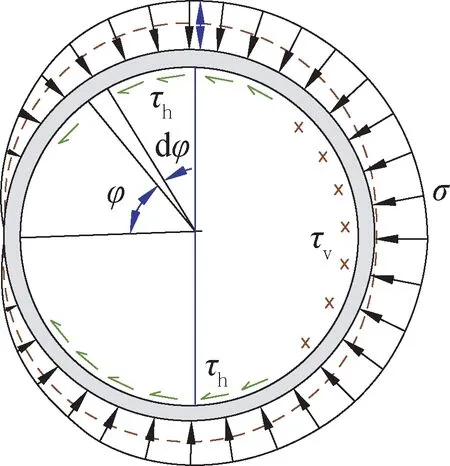
图9 灌浆段钢塔水平向受力状态Fig.9 Horizontal force state of steel tower in grouted section

图9 中虚线为产生水平方向摩擦力的接触压，大小为：

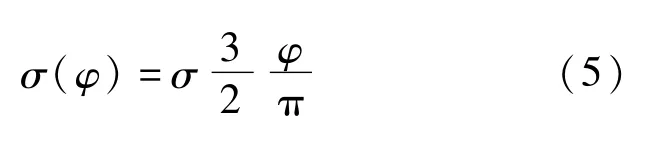
塔筒所受水平向摩擦力大小为：

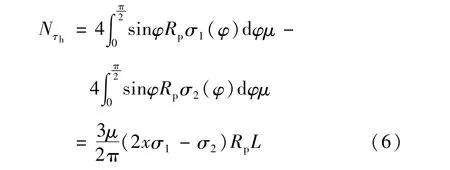
由钢塔最下端截面的剪力平衡得：

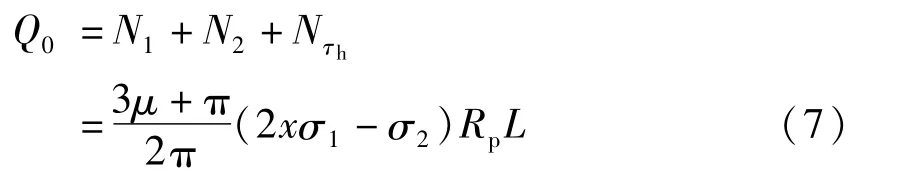
由灌浆压力N1、N2在连接段产生的弯矩可以表示为：

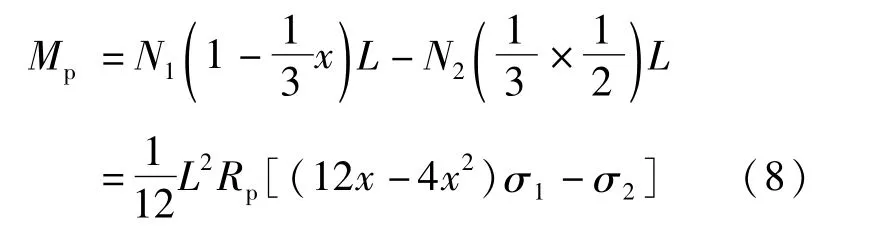
竖向摩擦力产生的弯矩可以表示为：

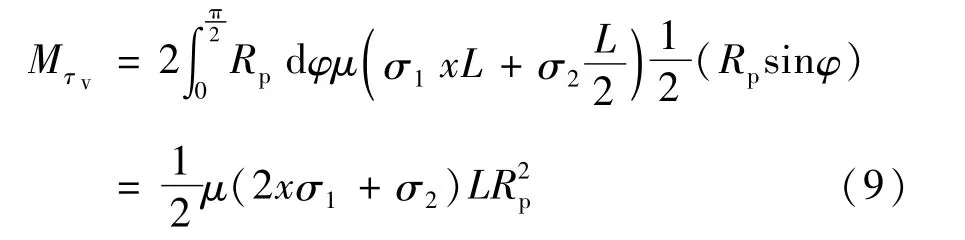
水平向摩擦力产生的弯矩为：

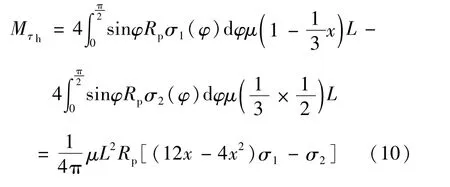
假定连接段内作用的剪力Q0一定，根据钢塔连接段下端中间位置力矩平衡，可以得到：

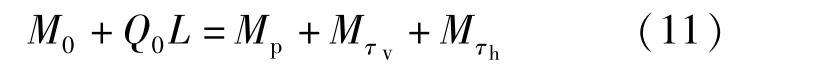
通过式（7）～式（11）可以得出：

上侧受压段最大平均接触压为：

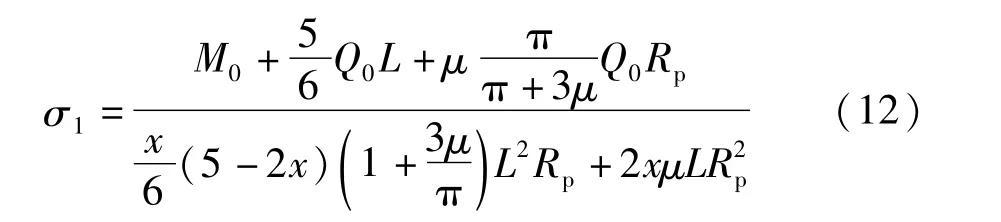
下侧受压段最大平均接触压为：

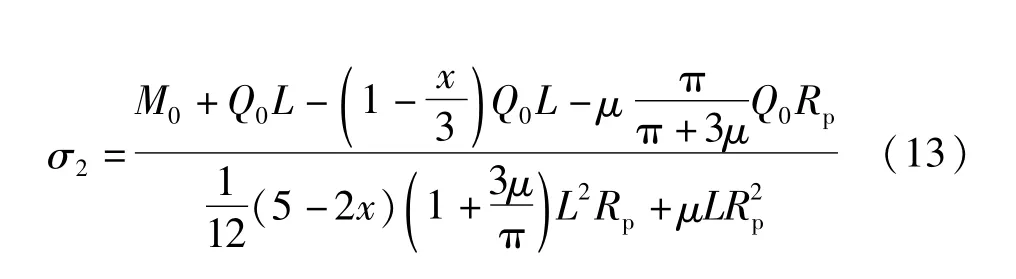
4.3 对比验证

由式（2）描述了接触压的分布规律，式（12）、式（13）分别求出了上下侧最大平均接触压大小，由此可以求出完整的接触压沿高度分布。如图10所示，以外侧混凝土厚度tc分别为600mm、1600mm、2600mm为例，对比θ ＝0°和θ ＝180°位置的接触压有限元计算结果、DNV规范公式结果以及本节推导公式计算结果。除上下端部应力集中范围外，有限元的分析结果与本节推导的解析结果基本一致，由此说明了理论分析是正确的。由图10 可知，依照DNV规范计算的最大接触压结果比有限元分析结果偏小。因此，在该类灌浆连接段如果直接使用DNV 规范中以接触压为基础推导的承载能力极限状态下的局部最大接触压、拉伸应力等公式，计算值都会比真实值偏小。

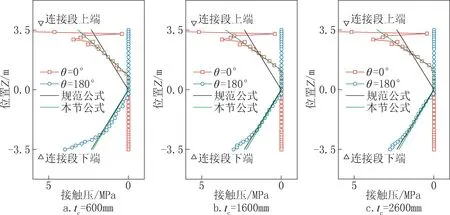
图10 灌浆段接触压竖向分布Fig.10 The contact pressure of connection

5 结论

本文针对钢-混组合结构发电塔结构的过渡段受力问题，研究了新型灌浆连接形式中连接段接触压的分布及大小。通过有限元软件ABAQUS模拟灌浆连接段并进行了理论计算，得出以下结论：

1.与传统海上风电灌浆套管相比，由于外侧混凝土的存在，该新型结构灌浆连接段接触压在竖向的分布明显不同，随着外侧混凝土变厚，连接段上侧受压部分接触压分布区域变小。但当外侧混凝土达到一定厚度后，外侧混凝土厚度的变化对接触压的影响将趋于稳定。

2.在掌握接触压分布规律的基础上，推导了上下两侧最大接触压的计算公式。通过有限元模拟与计算结果对比验证了本文推导公式的正确性。

3.由公式对比分析可知，以往规范对于该新型结构灌浆连接段并不适用，可能会高估该结构连接段的承载能力。本文的成果为钢-混组合结构连接段设计提供了一定的参考。