计算方法对钢筋混凝土圆管涵受力分析的影响研究

唐杨 王国炜 钟华栋 唐彬

1.五峰土家族自治县农村公路管理所 宜昌443413

2.济南金衢公路勘察设计研究有限公司 250101

3.四川携源建筑工程设计有限公司 成都610000

4.湖北屹峡峰建设工程有限公司 宜昌443000

引言

钢筋混凝土圆管涵是较为常见的涵洞形式，由于方便装配式施工、圬工数量少、造价低［1］，广泛应用于公路工程和农田水利工程［2-4］。

查阅相关文献发现：钢筋混凝土圆管涵的受力分析大都通过在土体与钢筋混凝土圆管涵的交界面设置接触对考虑土体与钢筋混凝土圆管涵的接触非线性。许庆虎［5］、马祖桥［6］、颜丹青［7］均以某钢筋混凝土圆管涵为研究对象，采用ANSYS有限元软件建立实体有限元模型，在土体和钢筋混凝土圆管涵的表面设置面-面接触单元来反映土体与钢筋混凝土圆管涵的相互作用。当考虑土体与钢筋混凝土圆管涵的接触非线性时，计算较为复杂，收敛较为困难。与钢筋混凝土圆管涵较为相似的波纹钢管涵，在其计算分析中，骆志红［8］、彭立［9］等学者忽略了波纹钢板与土体的滑移，不考虑接触非线性，直接将波纹钢板与土体共节点处理，而钢筋混凝土圆管涵的受力分析较少采用这种简化处理。

本文以某农村公路的钢筋混凝土圆管涵为研究对象，采用考虑接触非线性的计算方法和共节点处理的简化方法分别对其进行计算分析，对比两种计算方法下钢筋混凝土圆管涵受力情况的差异。

1 工程概况

某农村公路的钢筋混凝土圆管涵纵向长10m，圆形截面的直径为1.2m，其中壁厚0.1m。钢筋混凝土圆管涵的纵向有32 根φ8 通长钢筋和2 根10 螺旋钢筋，螺旋钢筋旋转一周的纵向伸长量为a ＝13.3cm，钢筋混凝土圆管涵的配筋情况如图1 所示。

图1 钢筋混凝土圆管涵（单位： cm）Fig.1 Reinforced concrete circular pipe culvert（unit：cm）

2 分析思路

钢筋混凝土圆管涵的有限元模型采用Midas FEA建立。钢筋的本构模型考虑为弹性模型，弹性模量为210GPa，容重为78.5kN／m3，泊松比为0.3。钢筋混凝土圆管涵采用C30 混凝土，混凝土的本构模型考虑为总应变裂缝模型，弹性模量为30000MPa，容重为25kN／m3，泊松比为0.2，受拉函数采用常数函数，受压函数采用Thorenfeldt函数，其受压应力-应变关系如图2 所示，图中fp为混凝土的抗压强度标准值。土体的本构模型采用摩尔-库仑模型，弹性模量为81MPa，容重为19.3kN／m3，泊松比为0.25，粘聚力为118kPa，摩擦角为22°，剪膨胀角为0°。

图2 混凝土受压本构关系Fig.2 Concrete compression constitutive relation

根据圣维南原理，取一定土体范围进行建模，圆管涵四周的土体至少为一倍管径的厚度［8］，钢筋混凝土圆管涵左、右侧的土体厚度取2.4m，上、下侧的土体厚度取1.4m，钢筋混凝土圆管涵的管轴方向取1.0m，钢筋混凝土圆管涵和土体的几何模型建立后采用自由网格划分技术划分为四面体单元。螺旋钢筋采用面面交线的方法建立几何模型［10］，然后采用自由网格划分技术划分为钢筋单元，不考虑钢筋与混凝土的滑移［11］。模型一不考虑钢筋混凝土圆管涵与土体的接触非线性，将钢筋混凝土圆管涵与土体共节点连接；模型二设置接触对，将钢筋混凝土圆管涵与土体考虑为面-面接触，将圆管涵的外表面定义为主面，土体接触面定义为从属面，贯穿类型选择轴对称一般接触，表示两个面粘接在一起，可以适用于计算中反复粘接、分离的情况，圆管涵与土体之间的静态摩擦因子设置为0.4，刚度比例因子设置为1.0。模型一和模型二表面上看相同，但在钢筋混凝土圆管涵与土体的边界上处理不同，处理为接触时边界的同一位置有两个节点，处理为共节点时边界的同一位置仅有一个节点。有限元模型如图3 所示，共计70486 个单元。

图3 有限元模型Fig.3 Finite element model

在边界上，将土体的底部固结，左、右两侧限制水平位移。在荷载上考虑自重和汽车荷载。汽车荷载施加于钢筋混凝土圆管涵上部土体的表面，采用面压力施加，面压力的范围考虑为一个轮载的接触面积0.6m ×0.8m，压力总量偏大地考虑为120kN。分析工况设置为非线性静力分析，计算方法采用Newton Rapson 迭代法，荷载步骤数设置为5，最大迭代步骤数设置为100。

3 两种计算模型的对比分析

3.1 变形分析

为了方便分析钢筋混凝土圆管涵的变形，对钢筋混凝土圆管涵的节点位置进行编号，圆管涵中间截面的最左侧节点编号为1，最右侧节点编号为2，最上侧节点编号为3，最下侧节点编号为4，节点分布示意如图4 所示。

通过计算，对模型一和模型二分别提取钢筋混凝土圆管涵节点1 和节点2 的水平位移如图5a 所示，提取钢筋混凝土圆管涵节点3 和节点4 的竖向位移如图5b所示。将节点2的水平位移减去节点1 的水平位移得到钢筋混凝土圆管涵的水平变形，将节点4 的竖向位移减去节点3 的竖向位移得到钢筋混凝土圆管涵的竖向变形，钢筋混凝土圆管涵的变形计算结果如图5c所示。水平位移由节点1 指向节点2 为正值，竖向位移由节点4 指向节点3 为正值。

由图5a 和5b 可以看出，在相同的节点位置，模型二的位移值大于模型一的位移值，随着荷载系数的增加，模型一与模型二的位移差值越来越大。由图5c 可以看出，模型二的圆管涵结构变形大于模型一的圆管涵结构变形，随着荷载系数的增加，模型一与模型二的结构变形差值越来越大。当荷载系数为1 时，模型一的水平变形为0.29mm，竖向变形为0.32mm；模型二的水平变形为0.38mm，竖向变形为0.41mm。由此可见，模型二的水平变形比模型一的水平变形大31.03%，模型二的竖向变形比模型一的竖向变形大28.13%。根据以上计算结果发现：模型二中钢筋混凝土圆管涵的结构变形比模型一大。

图4 节点分布示意Fig.4 Node distribution diagram

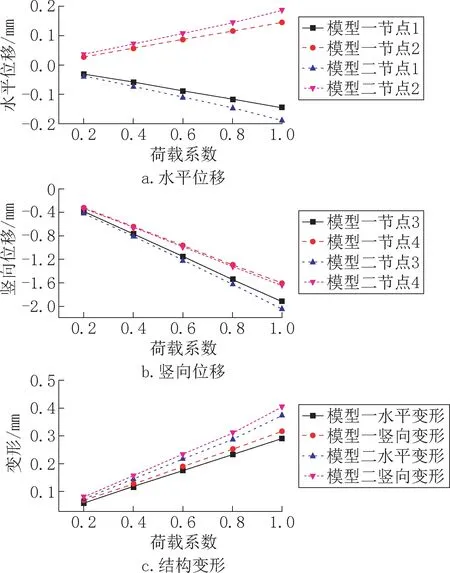
图5 钢筋混凝土圆管涵的位移和变形Fig.5 Displacement and deformation of reinforced concrete pipe culvert

3.2 应力分析

通过计算，对模型一和模型二分别提取钢筋混凝土圆管涵的第一主应力最大值如图6a 所示，钢筋的应力最大值如图6b 所示，其中拉应力为正，压应力为负。

图6 钢筋混凝土圆管涵的应力Fig.6 Stress of reinforced concrete pipe culvert

由图6a 可以看出，随着荷载系数的增加，钢筋混凝土圆管涵的第一主拉应力和第一主压应力最大值均呈现增大趋势，第一主拉应力最大值的增长速度大于第一主压应力最大值的增长速度。当荷载系数达到0.8 时，模型一的主拉应力最大值接近C30 混凝土的抗拉强度标准值，模型二的主拉应力最大值达到C30 混凝土的抗拉强度标准值。当荷载系数达到1.0 时，模型一的主拉应力最大值才达到C30 混凝土的抗拉强度标准值。由图6b 可以看出，随着荷载系数的增加，钢筋混凝土圆管涵的钢筋应力最大值呈现增大的趋势，模型二的钢筋应力最大值大于模型一的钢筋应力最大值。当荷载系数为1 时，模型一的钢筋拉应力最大值为21.38MPa，钢筋压应力最大值为23.90MPa；模型二的钢筋拉应力最大值为31.19MPa，钢筋压应力最大值为27.84MPa；模型二的钢筋拉应力最大值比模型一大45.88%，钢筋压应力最大值比模型一大16.49%。

由于模型一和模型二的第一主应力分布较为相似，仅提取荷载系数为1 时模型二的第一主应力云图如图7 所示。由图7 可以看出，钢筋混凝土圆管涵的主拉应力最大值主要出现在左、右侧的外缘和上、下侧的内缘。

图7 荷载系数为1 时模型二的第一主应力（单位： N／mm2）Fig.7 The first principal stress of model 2 when the load factor is 1（unit：N／mm2）

3.3 裂缝宽度分析

通过计算，对模型一和模型二分别提取钢筋混凝土圆管涵的裂缝宽度如图8 所示，模型二在荷载系数为0.8 和1.0 时的裂缝分布如图9 所示。由图9 可以看出，模型一在荷载系数为1.0时才出现混凝土裂缝，主要出现在钢筋混凝土圆管涵上、下侧的内缘，其裂缝宽度最大值为1.81 ×10-3mm。结合图8 可以看出，模型二在荷载系数为0.8 时就出现混凝土裂缝，刚开始主要出现在钢筋混凝土圆管涵上、下侧的内缘，然后出现在左、右侧的外缘，之后裂缝沿内、外环线扩展，荷载系数为1.0 时裂缝宽度最大值为3.97 ×10-3mm，为模型一裂缝宽度最大值的2.19 倍。

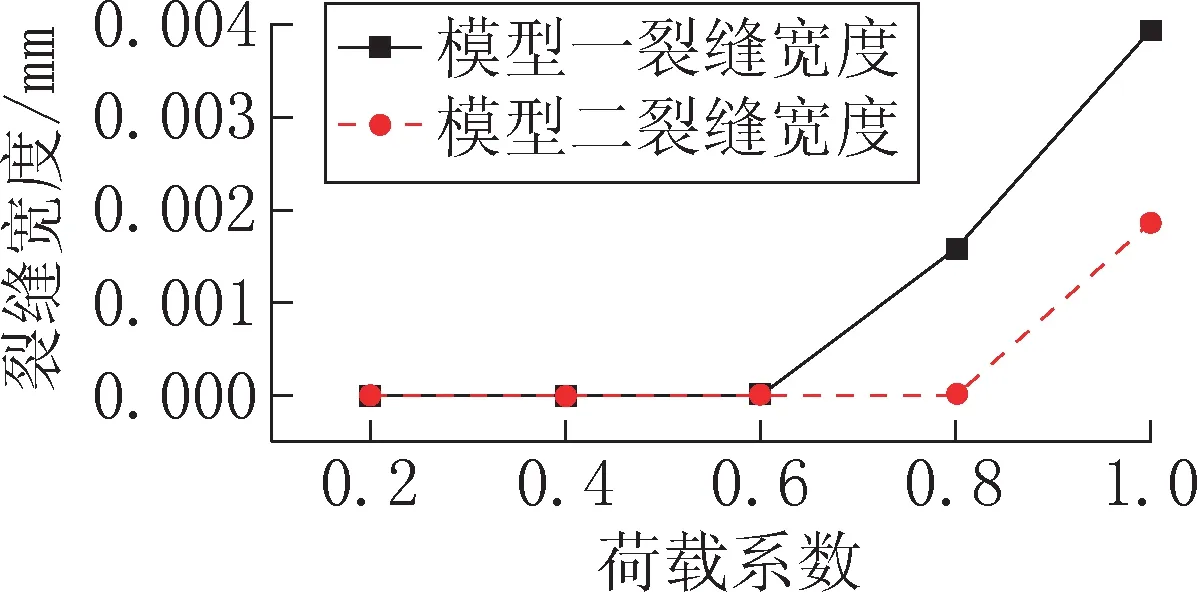
图8 钢筋混凝土圆管涵的裂缝宽度Fig.8 Crack width of reinforced concrete pipe culvert

图9 模型二的裂缝分布（单位： mm）Fig.9 Crack distribution of model 2（unit：mm）

3.4 接触力分析

模型一将钢筋混凝土圆管涵与土体之间考虑为共节点无法得到接触力的分析结果，在此仅对模型二提取钢筋混凝土圆管涵与土体的水平接触力最大值和竖直接触力最大值如图10 所示。荷载系数为1.0 时的水平接触力和竖直接触力分布如图11 所示。

图10 钢筋混凝土圆管涵的接触力Fig.10 Contact force of reinforced concrete pipe culvert

由图10 和图11 可以看出，钢筋混凝土圆管涵左侧和右侧的水平接触力最大值较为接近，上侧的水平接触力比下侧的水平接触力小；上侧的竖直接触力最大值比下侧的竖直接触力最大值大。当荷载系数为1.0 时，上侧的接触力最大值为231.17N，下侧的接触力最大值为186.24N，上侧的接触力最大值比下侧的接触力最大值大24.12%。当荷载系数为1.0 时，水平接触力最大值为58.70N，竖直接触力最大值为231.17N，为水平接触力最大值的3.94 倍。

图11 荷载系数为1 时的接触力分布（单位： N）Fig.11 Contact force distribution when the load factor is 1（unit：N）

4 结论

以某农村公路的钢筋混凝土圆管涵为工程背景，对比分析了两种不同计算方式下钢筋混凝土圆管涵的变形、应力、裂缝大小和分布，可以得到以下结论。

1.考虑钢筋混凝土圆管涵与土体的接触非线性时，钢筋混凝土圆管涵的水平变形相比不考虑接触非线性时增大31.03%，竖向变形相比不考虑接触非线性时增大28.13%，即考虑钢筋混凝土圆管涵与土体的接触非线性时计算得到的结构变形偏大。

2.无论是否考虑钢筋混凝土圆管涵与土体的接触非线性，混凝土的第一主应力最大值均达到其抗拉强度标准值，但考虑钢筋混凝土圆管涵与土体的接触非线性时，普通钢筋的拉应力比不考虑接触非线性时增大45.88%，压应力比不考虑接触非线性时增大16.49%。

3.考虑钢筋混凝土圆管涵与土体的接触非线性时，钢筋混凝土圆管涵的裂缝宽度是不考虑接触非线性时的2.19 倍，但无论是否考虑钢筋混凝土圆管涵与土体的接触非线性，其裂缝宽度均在允许范围之内。

4.考虑钢筋混凝土圆管涵与土体的接触非线性时，可以得到钢筋混凝土圆管涵与土体的接触力，更加符合结构的真实受力状态。由于钢筋混凝土圆管涵多为带裂缝工作，结构计算中必须考虑材料非线性，在此基础上再考虑接触非线性将显著增加计算的收敛难度，故而在对计算结果要求不是很高或硬件条件达不到时，也可以不考虑钢筋混凝土圆管涵与土体的接触非线性，采用共节点简化接触关系，但其计算结果是偏于危险的，需要对计算结果考虑一个放大系数才可使用。从计算结果来看，考虑2作为放大系数较为合适。