“证据推理”能力的水平框架构建
罗玛

摘要: “证据推理”能力是在科学学习过程中,从已有经验、问题情境中识别、转换、形成证据,利用证据进行推理,从而获得结论,解决问题的关键能力。研究分别阐释了“证据”与“推理”的复杂性结构,整合建构出“证据推理”能力的初步框架。应用德尔菲调查法,展开三轮咨询,对框架进行审视和检验,逐步获得专家共识,形成科学的、可操作的、多水平递进的“证据推理”能力框架。该水平框架是能力测评工具开发和数据分析的依据和基础,研究为能力素养评价工作提供了新的思路借鉴。
关键词: 证据推理能力; 水平框架; 德尔菲法; 复杂性
文章编号: 1005-6629(2021)03-0013-06
中图分类号: G633.8
文献标识码: B
1 引言
科学推理能力、思维的培养和发展在当前国际科学教育改革中处于十分关键、重要的地位。我国理科课程对推理思维的培养表示高度的重视[1],在各科目最新的课程标准文件中有着不同但明确的表达,如数学学科中的“逻辑推理”,物理学科中的“科学思维”,化学学科的“证据推理”,生物学科的“理性思维”等。虽然表达各异,但对于科学研究的本质过程与思维要求,学界已有共识,是科学学习所必要的高阶思维,也是科学素养的体现。
识别、筛选证据,转换、形成证据,应用、评价证据等过程是科学探究和科学实践的重要环节,是科学工作者展开科学研究、得到科学发现的基本过程,关注于“基于证据的推理”能力,即“证据推理”能力或素养(Evidencebased Reasoning Competence, ERC),对科学学习和教学具有重要意义。在科学学习中,从已有经验、问题情境中识别、转换、形成证据,利用证据进行推理,从而获得结论,解决问题的能力表现,即“证据推理”能力[2]。可见,可以从“证据”与“推理”两方面阐释这一构念。
查阅文献发现,有研究者结合了证据与推理的双重复杂性,在课标基础之上,利用SOLO分类理论对证据推理的能力水平进行重新划分[3]。而且,“科学推理”或“科学思维”的测评研究较多[4,5],围绕于“证据推理”能力的评价研究则比较缺乏。因此,本研究尝试建构“证据推理”能力的水平框架,以期为教学评活动提供一定参考。
2 研究设计
本研究的目的在于构建一个可供测评的、科学的“证据推理”能力水平框架,包括框架的初步建立和修正两个阶段。第一阶段,在理论探讨的基础之上,将从“证据”与“推理”本身的复杂性结构出发,加以整合,提出初步的水平框架;第二阶段,通过专家调查法(德尔菲法)对框架进行修正和完善。
2.1 德尔菲法
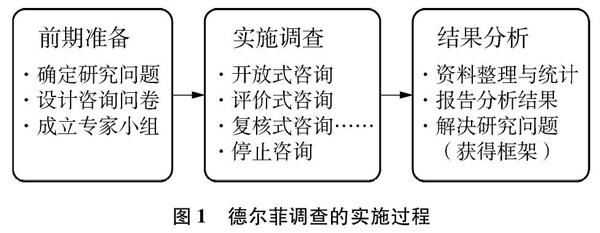
德尔菲法(Delphi method)是常用的专家调查法,它针对某一特定问题经过至少两轮的匿名式咨询,反复调查和反馈,一步步求同和修正,最终使得专家们的观点逐渐“聚敛”成一致、稳定的意见[6]。根据已有研究及该方法的程序性要求[7],本研究的调查过程包括三个主要环节,如图1所示。
在本研究中,德尔菲法所要解决的主要问题即对初步构建的“证据推理”能力水平框架进行审阅、修正,提出意见并最终达成共识。这一初步框架是通过文献梳理和理论探讨获得。
2.2 咨詢问卷
根据研究问题,设计出《“证据推理”能力水平框架的咨询问卷》,问卷包括以下3部分内容: 咨询目的和研究问题、初步构建的框架及相关说明、维度及水平认同度评分表。后一次咨询将会结合前一次咨询对问卷作出调整。
此外,在第一次咨询时还调查了专家的基本情况,及其对研究问题的判断依据及熟悉程度。其中,判断依据是从理论分析、实践经验、同行了解和个人直觉四个维度[8]进行调查。问卷通过电子邮件发放,明确说明研究问题和需要匿名返回的文本要求。
2.3 专家选择
研究邀请了科学教育研究和教学实践领域的专家16名,组成咨询小组。有领域内的专家学者,其中教授4名,副教授4名(含境外专家1名),讲师2名;学科教师,其中高级教师2名(其中特级1名),一级教师2名;地区高中教研员2名,曾是经验丰富的优秀教师。专家工作年限在8~25年。
2.4 数据处理
经第一轮开放式咨询,获得问题和意见,研究者筛选、整理问题,对框架进行修正和讨论;将问题列表和初步修改的框架整理后,组成第二轮咨询问卷,即进行评价式咨询;如此反复,直至形成统一的建议,停止咨询。
针对咨询过程,计算专家的积极系数(问卷回收率)及权威系数(判断依据和熟悉程度的均值)。“认同度”按5点Likert量表收集数据,计算每一轮每一指标上的均值和协调系数。
3 构建初步框架: 整合证据与推理的复杂性
通过理论文献分析,研究从“证据”与“推理”两方面的复杂性结构出发,为整体描绘“证据推理”能力的内涵和结构提供基础。
3.1 “证据”的复杂性
所谓“证据”是可获得的事实与信息,既有其本身的固有属性,例如无法变更的历史事实、目前已获得验证的科学真理,同时也存在变化发展的潜在可能,体现了科学发展的暂时性、动态性和待检验的本质(nature),如还有待实验证伪、证实的科学假设。根据问题解决的心理学机制研究,面对一个问题,学生根据生活经验对问题的情境做出理解和表征,称之为情境模型(situation model),并不涉及题目的具体关系,主要是定性地表征[9]。将证据来源作为问题的情境,其呈现方式反映了证据的复杂性(complexity of evidence,以下简称CE)。
情境(context)指的是对于待解决的问题设置或编织出的“情节”(scenario)[10],这些情节中蕴含着信息,它们对于问题解决而言,可能是必要的(necessary),也可能是不必要的(unnecessary)[11]障碍或限制(constraints)。诸多研究和国际项目(如PISA)、课程改革文件等,都强调问题的情境创设,由此带来的教学内容、教学方式变革也深受瞩目。例如情境化教学,在基于问题解决的教学过程中,为学生提供强支持(strong contextual support),以及参与复杂推理的机会(opportunities to engage complex reasoning)将会影响学生的学习[12]。
“证据”是问题解决的必要信息、知识,在纷杂的情境中,识别出问题解决的关键信息,即“证据”,是问题解决的首要步骤。在问题的情境中,证据或是显而易见(explicit),或是隐而待发(implicit),这反映的是证据的显性化程度(exposure),越显性则说明证据的识别提取越容易,证据的复杂性则越低。Salgado指出情境的显性与否(explicit or implicit)会影响学生的情境参与度(context engagement),即特定情境下学生解决问题的热情和渴望,进而影响学生的成就表现。
此外,该研究者提出情境熟悉度(context familiarity)为情境影响的维度之一,虽然研究者表示尚未有确定而统一的定义,但指出了与学生的生活经验和知识体系密切相关的情境是熟悉的(familiar),而相反地,非生活经验的情境即为陌生的(unfamiliar)[13]。
在解决问题过程中所需证据的多寡也是决定其复杂性的因素之一,这里所强调的数量(quantity)是所需要的证据,而非问题中所直接呈现的信息量多少。当情境中直接呈现的信息量大,但所需的证据单一(single),而且可以从这些信息中直接找到,则其复杂性要求并不高,虽然相比于信息量较少的情境,此时增加了识别证据的困难,但并没有“线索不明”(implicit)带来的障碍大。因此,如果所需证据单一但不够显化,需要从给定的情境信息中挖掘,其复杂性要求显然较高,这时如果问题情境中的信息量大,显然会增加难度,而且直接的影响是降低了证据的显现程度(exposure)。
基于以上分析,研究从三个方面去刻画证据的复杂性,涉及到证据的显现程度(exposure)、情境熟悉度(familiarity)以及所需证据的数量(quantity),由此构建出三维坐标图。如图2所示,每个维度均有两个不同的向度(指标),以英文首字母简略表示,将不同指标之间排列组合之后,有8种形如“XYZ”的可能表征存在,据此反映出多层次的证据复杂性。例如,当学生解答问题时,遭遇一个陌生情境(U),线索不明(I),而且所需利用的证据较多(M),在这种复杂性表征的组合情况下(MIU),其解决问题的困难程度自然最高;若学生遇到的是熟悉的情境(F),仅需单一证据(S),而且显而易见(E),这种证据复杂性(SEF)对思维的要求最低。
3.2 “推理”的复杂性
识别出问题情境中的“证据”之后,即利用证据这一前提开始“推理”,最终得出结论。解决问题的过程可以简单表示为: 证据→结论(E→C),这中间必须经历的思维过程即“推理”。问题解决的复杂性或者难易程度,受到证据复杂性(CE)的影响,也必将由过程的复杂性,即推理的复杂性(complexity of reasoning,以下简称CR)所决定。
从逻辑学视角来看,根据推理前提所含判断的数目可以区分出直接推理(immediate inference)和间接推理(mediate inference)。直接推理是一种最简单的演绎推理[14],它是以一个判断作为前提的推理;间接推理是以两个或两个以上判断为前提的推理,包含大多数的推理[15]。鑒于此,本研究将“基于证据进行推理”的过程分为直接推理(direct reasoning)和间接推理(indirect reasoning),区别于逻辑学范畴内的表达和阐释,因为逻辑学所关心的推理的有效性问题,仅就推理的形式结构而言[16],而在本研究,或实际问题解决过程中,我们还需要关心一个具体推理所包含的前提、结论在内容和意义上的联系,即由证据推理出结论这一过程的科学性、正确性、完整性要求等。
本研究中,直接推理(direct reasoning)处理的是证据(单一或多重)或题目给定信息(尚未确定是否可以作为证据)之间的简单关系;间接推理(indirect reasoning)是处理证据之间的复杂关系,必然涉及多重证据。简单关系所要求的推理复杂性较低,复杂关系的处理则需要正确建立多重证据之间的联系,这种联系可能是显性的,也可能隐含在情境之中,由此增加了推理的复杂性要求。
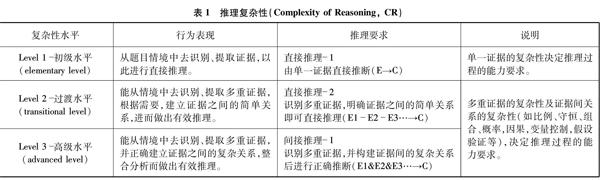
我们所探讨的推理复杂性不是在个体阶段发展的纵向层面,而是围绕着学生推理思维的行为表现,可以说是在某个特定阶段(根据实证研究对象的年龄段而定)的个体进行推理时所表现出的不同能力水平,是处于某一进程阶段时的具体化的行为水平,同样具有层次性、发展性。本研究基于推理的直接与间接之分,将推理复杂性划分为三个层级的复杂性水平,如表1所示。
识别多重证据,并构建证据间的复杂关系后进行正确推断(E1&E2&E3…→C)多重证据的复杂性及证据间关系的复杂性(如比例、守恒、组合、概率,因果,变量控制,假设验证等),决定推理过程的能力要求。
从表中可以看到,推理复杂性的过渡水平(Level 2)涉及的是多重证据直接推理,标记为“直接推理-2”,在初级水平(Level 1)的推理要求之上有所提升,区别主要体现在所需的证据数量。而“间接推理-1”则要求处理多重证据之间的复杂关系,定义为高级水平(Level 3)。这两种情况之间的差异主要由多重证据的复杂性(CE)来表征,因此用不同的符号连接多重证据(E1-E2-E3与E1&E2&E3)以示区别。
由此,进一步说明了推理过程不能完全脱离于证据,即使是在推理的复杂性要求上仍有必要考虑证据是隐性还是显性、熟悉还是陌生的影响。是以,在后面构建“证据推理”能力框架时应整合两方面的复杂性。
3.3 “证据推理”能力的初步框架
“证据推理”强调的是基于证据进行推理,“推理”是主体思维过程,“证据”是必备前提条件,本研究认为其测评框架应以“推理”为主线,以“证据”为其影响的分类标尺。因此,基于前面的分析论述,将三维度八类别的证据复杂性(CE)与推理复杂性(CR)的三水平相互匹配与勾连,形成多层次递进的“证据推理”能力水平,进而构建出初步的“证据推理”能力框架(Framework of Evidencebased Reasoning Competence, FERC),如表2所示。
证据的复杂性直接或间接地、或多或少地都将影响推理的复杂性,二者互相交联着影响、表征“证据推理”能力。单一证据(S)所指向的能力水平较低(Level 1),多重证据(M)则指向更为复杂、要求更高的“证据推理”能力(Level 2~Level 3)。当情境陌生时(U),增 加了证据的复杂性,由此,在处理同类关系、应用同种推理方式的情况下提高了推理的复杂性,继而表征出不同层次的“证据推理”能力。本研究认为,相比之下,情境陌生(U)造成的困难程度不及证据的隐性化(I),这点可以从一些研究发现中获得支持[17]。
情境的熟悉度则更多地体现题目表面的特征,如某种经验、某个现象、某个事实等。如果“熟悉”(F),对于学生解题、解决某个实际问题、做出决策更为便利,因为情境易于理解,但也可能会因为思维定势而影响学生的问题解决,这一点在本研究中不多加讨论,我们认为情境熟悉(F)比不熟悉(U)更利于學生问题解决,即要求较低。
证据显现程度(exposure)反映的是证据与情境载体的融合情况,比情境熟悉度更为复杂而深入。所需的证据越隐性化(I)说明它们越不容易从既定的情境中被识别,在头脑中进行转换而产生图式(有效推理所必需)时的障碍更多,更加“耗费精力”。因此,同样是复杂性的增量,陌生化情境(U)不及证据隐性化(I)明显,以推理水平为主线进行刻画的“证据推理”能力也在此有所区别,如表2所示,证据隐性化指标所指向的能力水平高于同等情况下的陌生指标。
4 调查结果分析: 框架的修正与确立
4.1 调查的数据结果
研究共有三轮咨询,每轮咨询间隔大约半个月。在第一轮咨询问卷中对初步构建的框架进行了解释说明,并附上了图2、表1和表2,围绕框架,由专家自由发表意见并作说明,意见返回后,如遇不明,再单独请教,以保证研究者获得明确的问题列表。第一、二轮发放问卷16份,回收16份,积极系数为100%,第三轮回收14份,系数为87.5%,根据专家自我报告的判断依据与熟悉程度,计算得到权威系数为0.91,说明专家组的积极程度和权威程度均较高。
针对初步框架的结构要素和层次水平,专家意见不一,认同度的数据结果显示,三轮的框架水平认同度均值分别为3.82~4.12, 4.10~4.75, 4.55~5.00,认同度较高,且在不断上升;卡方分析发现每一轮的协调系数均显著(p<0.05)。
4.2 问题筛选与讨论
通过前两轮咨询,筛选、确认专家反馈的问题,整理摘录主要意见有:
(1) 根据框架,证据是隐性的就意味着“间接推理”的要求吗?像是编码MIF的证据复杂性,就都达到了高级水平。
(2) MEU下分两种情况,“较复杂”关系在“推理的复杂性”中并没有说明,前后似乎不一致;MIF与MIU都需要“间接推理”,又包括简单关系和复杂关系,这一点也与“推理的复杂性”的说明不一致。
(3) 在各级水平下,a、 b、 c之间的差距不同,或者说水平所划分的依据不太统一。如果差距不明确,何必划分3个子水平。
重新审视初步框架,反思了以上意见。根据前面的阐释,“推理复杂性”(CR)中隐性化证据(I)增加了学生的解题困难,即提出了更高的“证据推理”能力要求,其水平更高,但“间接推理”是论及推理过程的要求,并非隐性的证据之间就会存在复杂关系(间接推理),原先框架中编码MI-Z注: 此编码形如“XYZ”,编码包含3个字母,此处表示证据多重(M)、隐性(I),第3个字母“Z”可以表示熟悉(F)或陌生(U)。的证据所表征的能力水平则不太妥当。
多重证据(M)不一定是需要间接地、多步地推演,但的确比单一证据(S)复杂;多重证据之间的关系简单,也会降低推理要求,即推理复杂性也将受到推理关系是简单还是复杂的影响,这并不能简单地由证据是否显性化决定。这一点在我们初步建构框架时,虽然能意识到,却还是忽视了。在隐性的多重证据(MI-Z)之下,也有可能只需要处理证据之间的简单关系(直接推理-2),这与处理显性多重证据(ME-Z)之间的简单关系相比,的确更为复杂,但未能构成高级水平(Level 3)与过渡水平(Level 2)之间的差距。这些误区或混乱,造成了框架水平之间的不恰当。
“证据推理”能力的水平要求是将证据复杂性(CE)与推理复杂性(CR)进行整合而形成的。因此,该能力框架应以二者为基础,保持统一。根据推理复杂性,三级水平所对应的推理要求分别是直接推理-1、直接推理-2和间接推理,而M-YZ并非只涉及间接推理,也存在直接推理-2的要求,那么就会产生能力水平与证据复杂性(CE)的交叉。
4.3 确立能力水平框架
根据以上咨询结果和问题反馈,研究者回应了专家的建议,并修正了能力框架,因情境熟悉度(familiarity)指标在证据复杂性的增量不明显,因此框架中弱化了熟悉(F)与陌生(U)对能力表征的影响,解决了原框架中各子水平划分不明的问题。之后,整合修改资料进行第三轮复核式的咨询,收到专家组的认同意见之后,停止本研究的咨询调查。
最终的“证据推理”能力框架(FERC)确立了6个水平,在每一级推理复杂性水平之下各有两个子水平(a与b),在证据复杂性上交叉体现,如表3所示。该框架是按照水平递增的顺序呈现,反映了学生“证据推理”能力的不同水平表现。
5 结语
基于理论探讨,本研究整合“证据”和“推理”两方面的复杂性,得到“证据推理”能力的初步框架。应用德尔菲调查法,对该框架进行三轮咨询,获得了可供参考和反思的意见。从而,对框架进行修正、完善,逐步形成科学的、可操作的、多水平递进的“证据推理”能力水平框架(FERC)。这一框架构建与修正的思路不同于课程标准中的素养水平划分,深入探讨了素养的内涵与结构本身,与其他学科核心素养并不勾连。由此,为其他学科核心素养的测评工作提供了思路、方法的借鉴。
该框架提供了一种深入认识“证据推理”能力的途径,也为能力测量工具开发和数据分析提供了依据和基础。可以通过解决不同难易度的“证据推理”问题来表征学生的不同能力水平,此框架则是编制问卷,进行评分的参照,是对学生表现进行区分的标尺。同时,未来研究中的实证数据和分析结果也将为本研究构建的能力水平框架提供更具体更全面的修正依据。
参考文献:
[1]核心素养研究课题组. 中国学生发展核心素养[J]. 中国教育学刊, 2016, (10): 1~3.
[2]羅玛. 从科学推理到证据推理: 内涵的探讨[J]. 化学教学, 2019, (9): 3~6.
[3]方弯弯, 龚正元. 关于化学学科证据推理能力及评价的思考[J]. 化学教学, 2019, (12): 15~20.
[4]邓磊, 包雷. 基于科学思维能力评价的美国理科主流试题类型比较及启示[J]. 物理教师, 2018, 39(10): 5~11.
[5]张静, 丁林, 姚建欣. 国外科学推理研究综述及其对素养评价的启示[J]. 上海教育科研, 2019, (7): 20~24+29.
[6]Bolger F, Wright G. Improving the Delphi process: lessons from social psychological research [J]. Technological Forecasting & Social Change, 2011, 78(9): 1500~1513.
[7]曾照云, 程安广. 德尔菲法在应用过程中的严谨性评估——基于信息管理视角[J]. 情报理论与实践, 2016, 39(2): 64~68.
[8]何鸽飞, 孙吉, 黄娟娟, 陈恒, 胡立强, 邓桂明. 基于Delphi法的抗菌药物使用合理性评价指标体系研究[J]. 中国药房, 2019, 30(14): 1881~1885.
[9][11]和美君, 刘儒德. 论数学问题解决中情境模型与问题模型的关系[J]. 心理科学, 2012, (3): 642~646.
[10][13][17]Salgado F A. Investigating the impact of context on students performance [C]. Opening up mathematics education research (Proceedings of the 39th annual conference of the Mathematics Education Research Group of Australasia), Adelaide: MERGA, 2016: 102~109.
[12]Choi J I, Hannafin M. The effects of instructional context and reasoning complexity on mathematics problemsolving [J]. Educational Technology Research and Development, 1997, 45(3): 43~55.
[14]彭漪涟. 逻辑学基础教程[M]. 上海: 华东师范大学出版社, 2008: 56.
[15]南开大学哲学系逻辑学教研室. 逻辑学基础教程[M]. 天津: 南开大学出版社, 2008: 68.
[16]黄士平. 简明逻辑学[M]. 武汉: 湖北教育出版社, 2005: 205.

