浅谈培养初中生数学规范解题的探究

邢双娜

摘要：培养初中生规范解题能力，不仅仅有助于学生的可持续发展，还能够有效地提高初中数学学科的教学质量。在数学教学的过程中，教师需要通过解题的规范性，帮助学生建立起一个灵活的思维，使学生能够抓好基础知识，在做题的过程中灵活地运用所学的数学知识解决数学问题。通过这样的教学过程使学生获得解题能力，提高学生的数学学习水平。本文立足于数学规范解题，从基本公式、关键词理解，列表法应用，不变量的思考以及规划运用图式五个角度，分析了有效的教学策略，从而使学生能够遵循科学解题的顺序，有目的、有计划地解题。

关键词：初中生;数学;规范解题;探究

中图分类号：G633.6  文献标识码：A文章编号：1992-7711（2021）06-011

美国教育学家波利亚认为，问题是数学的心脏。因此在进行教学的过程中，教师要注意的不是将知识强加给学生，而是教会学生如何灵活运用知识解决数学问题。而学生的灵活解决问题是需要遵循一定的规范，这样才能够使学生在数学学习的过程中，调动起自己脑海中的知识，针对不同的题型，采用不同的方式解题。因此在教学的过程中，教师与其对学生进行呆板空洞的知识教授，不如先从解题方法入手，引导学生规范解题的学习，从而使学生受益一生，最终实现学生自身数学学科核心素养的全面提升。

一、规范解题的作用

在现阶段的数学教学过程中，笔者发现很多学生做题不注重审题，明明很简单的问题，学生却做错了，还有的学生面对着数学题，一点思路都没有，往往一道简单题会耽误学生将近一节课的时间。这就体现了学生在学习的过程中并没有掌握数学解题规范。因此在教学的过程中，通过对学生数学规范解题的培养，首先能够使学生养成良好的数学解题习惯，从学生的题目阅读开始，使学生掌握一定的方式和方法，使学生在读题的过程中，能够充分地理解出题者的本意，使学生能够站在题目整体的角度分析原题，并且巧妙地将自己脑海中的知识进行调动，找到适合该题的解题方法。这样学生在进行活学活用的解题过程中就能够拥有明晰的解题思路，从而减少浪费时间的状况。对于初中生而言，他们面临着中考的压力，因此在教学的过程中，通过解题规范的教学，能够使学生在学习的过程中直击中考为学生的中考保驾护航，也能够使学生在中考的过程中，能够遵循一定的解题规范，做出大胆的尝试，从而促进学生的数学成绩提高。

《九年义务教育数学课程标准》明确指出，对学生的數学教学不能死板地停留在知识讲授方面，而是应该促进学生的知识探究，通过解题规范的培养，能够使学生掌握知识探究，和解题探究的方法，从而使学生在面对数学问题的过程中，更加充满信心，同时也促进了数学课程改革的发展。

二、初中生数学规范解题策略

1.利用基本公式

作为数学重要教学内容和解题方法的内容之一，公式在数学学习的过程中起着不可替代的作用。但是在学习的过程中，很多学生潜意识里认为公式是一个十分简单的东西，自己只要背过了就行。但是就是因为学生的这种想法，导致学生在解题的过程中，生搬硬套不会灵活运用。尤其是一些数学问题，乍一看上去似乎不能用数学公式解决，这时就需要学生在遇到问题之后，认真对原题给出的条件进行分析，从而思考是否能够采用公式解决问题。

例如下面一题：a-b=b-c=35，a2+b2+c2=1则ab+bc+ca=

在这一题当中，要求解的内容是ab+bc+ca的结果，学生可以首先通过已知条件分别求出a、b、c的值，但是这样的形式，计算量会很大。但是通过观察题中给出的条件，我们又发现，可以运用完全平方公式，将已知的内容进行整体的带入，通过带入，使学生能够更加简洁的求出结果。

在解题的过程中，我们可以得到已知条件a-b=35，b-c=35，那么，两个等式加起来，得到a-c=65，我们就能够得知（a-b）2+（b-c）2+（a-c）2=（35）2+（35）2+（65）2用完全平方公式展开，我们就能够得到ab+bc+ca的答案为-225

在这一题的解题过程中，就需要学生熟悉完全平方公式的结构特征，这样才能够使学生通过已知条件，来创造出三个完全平方和的等式，从而使学生更加简便地计算出结果，大大降低了计算的难度。

2.理解关键词汇

在数学解题的过程中学生自身的审题能力至关重要，因此在解题的过程中需要学生养成良好的审题习惯，在审题的过程中能够发现关键词，从关键词下手引导学生分析原题当中的条件，从而对题意有一个充分的认知。把握数学的本质和联系，从而提高学生的解题效率。

例如在下面这一问题的解题过程中，学生如果能够抓住关键词就能够更好地进行解题：两辆汽车从相距84千米的两地同时出发相向而行，甲车的速度比乙车速度快20km/h，半小时后，两车相遇，求两辆车的速度各是多少？

在本题当中，主要的内容是行程问题的相遇问题，因此在找关键词的过程中，学生需要注意原题当中的等量关系，本题当中的关键词是同时出发相向而行。

在数学学习的过程中，通过找寻关键词，通过关键词将数学语言翻译成通用语言，从而使学生能够更加清晰地了解到数学题的本意，提高学生的解题效率。

3.巧用运用列表

对于初中阶段的学生而言，数学仿佛就是一个既可爱又可恨的“敌人”，针对敌人就要选用合适的武器。在进行解题的过程中，运用列表法，通过表格，更加清晰的梳理题意，将复杂的问题变得简单化，从而避免错误的出现。在初中数学的解题过程中，常常会出现一些通过列式计算无法解决的问题，在这时候，就需要学生借助列表法，对原题当中给出的内容进行分析，从而帮助学生更好地解决问题。

例如在下面一个概率问题的解决过程中，就可以采用列表的形式解决：同时抛掷三枚硬币，求下列事件的概率：①三枚硬币全部正面朝上;②两枚硬币正面朝向，另外一枚硬币反面朝上;③至少有两枚硬币正面朝上。

在概率问题的计算过程中，学生需要首先将所有的可能性进行举例，然后在可能性的基础上，来找寻相应的条件，才能够更好地解决问题。这时学生使用列表法进行问题的解决，能够帮助学生更加清晰的对原题当中的内容进行分析，并且依照表格当中的内容进行思考，这样一来学生在学习的过程中就会变得更加有条理。初中是学生成长的关键时期，因此熟练运用列表解题方法，不仅对学生当前的数学学习有着很大的帮助，还能够对学生的其他学科，乃至学生的终身学习都有着很大的帮助。这样就能够把原题当中，毫无联系的内容建立起链接，从而准确、直观地找到答案。

4.感受不变量构建相等关系

动点问题一直是初中数学的热点问题，近几年的中考题目中，对学生的动点问题考察层出不穷。在中学阶段动点问题一直被学生称为“顽固分子”，很多学生发现在学习过程中，虽然自己对集合或函数的意义十分熟悉，但是在解题的过程中，只要出现关于动点的知识就大脑一片空白。这就需要教师在教学的过程中，结合实际的例题来为学生分析，引导学生感受不变量，从而构建出相等关系，这样才能使学生在解题的过程中找到有效的解题思路。

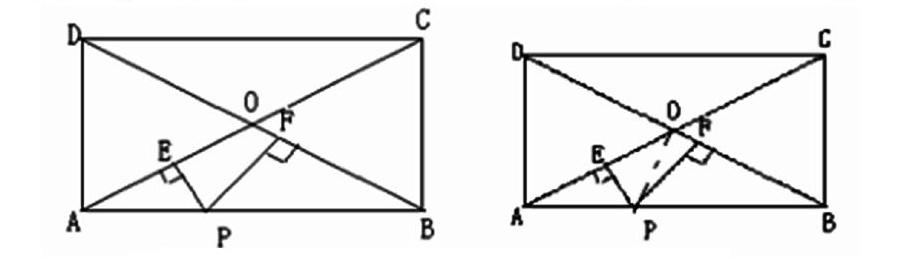
例如，在线面题型当中：已知矩形ABCD的对角线AC和BD相交与点O，点P是边AB上的一个动点，PE⊥AC且PF⊥BD，垂足分别是E和F，如果AB=4厘米，AD=3厘米，求PE+PF的值。

在解题的过程中，我们首先要连接OP，在连接过后我们突然发现，三角形AOP和三角形BOP的面积是会随着P点的运动而发生变化的，但是这两个图像的面积的和却是不变的，而我们需要求解的PE和PF又恰好是这两个三角形的高，并且，这两个三角形的底边OA和OB是相等的，并且不会随着动点的变化而产生变化。因此在求解的过程中，我们就可以通过变和不变，构建出新的关系。

因为矩形ABCD的对角线AC和BD相交于点O，且AB=4厘米，AD=3厘米，所以AC=2ab2+bc2=5，OA=OB=52，三角形ABO的面积为矩形的14也就是3平方厘米。因为三角形AOP的面积=12×OA×PE;三角形BOP的面积是12×OB×PF，所以最终可得PE+PF的值为125。

5.规划运用图式

对于初中生而言，视觉空间表征是一种有效的解题策略。而通过运用图式的方式就能够将一些抽象的数学问题，以具象的图片形式展现在学生的眼前。在解题的过程中，学生能夠从问题情境的感知到问题的深入理解，再到问题解决方法，获取这样的一个过程，解决数学问题。这样的形式不仅有助于学生快速理解数学问题的本质，还能够帮助学生在灵活的情境下，自由地进行知识的迁移。这种行为不论是对学生的知识获取还是对学生的知识运用能力都有着良好的促进作用。通过运用图式的规划，就能够使学生触类旁通，达到举一反三的目的。

例如在函数的解题过程当中，可以通过图式知道解题的思路。

例1：（广东省深圳市）已知二次函数 y=ax2+bx+3的图像分别与x轴交于点A（3，0），C（-1，0），与y轴交于点B，点D为二次函数图像的顶点。

（1）如图①所示，求此二次函数的关系式;

（2）如图②所示，在x轴上取一动点P（m，0），且1

（3）在图①中，若R为y轴上的一个动点，连接AR，则1010BR+AR的最小值   （直接写出结果）.

在第三部分的解答过程中，就可以通过构建直角三角形来解决。

我们可以连接BC，过点R做RQ⊥BC，垂足为Q。这样在二次函数当中就出现了两个直角三角形，一个是RT△CQA，一个是RT△BCO。我们知道C的坐标为（-1，0）这样就能够得到OC=1，OB=3根据勾股定理可以得知，BC的值，并且通过两个直角三角形得知△BQR与△AOB为相似三角形，进一步求得RQ与BR之间的关系，从而得知当A，R，Q三点共线时，值最小、这样就能够通过相似三角形的定理解出最小值。

通过图式的运用，就能够将复杂的函数问题，通过简单的三角形构建解决问题，从而使学生能够化繁为简。

综上所述，在进行数学学习的过程中，学生的解题规范，不仅能够提高解题效率，还能够使学生能够养成良好的解题习惯，这是对学生终身产生积极影响的一种方式。在新课改的背景下，对于学生的综合能力发展以及可持续发展的要求也越来越高，所以在数学教学的过程中，教师也要立足于学生的可持续发展，从学生的中考入手，帮助学生进行数学规范解题培养，从而使学生在解题的过程中能够遵循一定的规律，根据不同的题型，找寻最佳的解题方案，从而减少学生在解题过程中所浪费的时间，提高学生在解题过程中的效率和准确率，最终使学生获得综合的、可持续的发展。

参考文献：

[1]郑秋月.几何证明、尺规作图的解题规范与解题技巧——初中数学几何解题规范[J].考试周刊，2020（1）：92-93.

[2]李俊.新课程背景下初中数学教学中学生解题能力的培养探析[J].青少年日记（教育教学研究），2019（11）：185.

[3]吕玉坤.初中数学解题规范及解题策略——以初中数学概率为例[J].高中数理化，2019（12）：36.

[4]刘瑞美，王成功，李祥.面对中考找好支点把握重点突破难点——从数学核心素养的角度简述初中复习过程中的解题规范能力培养[J].高中数理化，2019（Z1）：16-19.

【陕西省第六批中小学幼儿园学科带头人培养对象专项课题《基于核心素养下的初中生数学规范解题的过程的策略研究》（课题编号：XDKT6154）】

（作者单位：咸阳市礼泉县英才初中，陕西 咸阳 713200）