鼠笼式弹性支承-圆柱滚子轴承-转子系统振动分析
杨世娇
(沈阳泰尔达建材有限公司,辽宁沈阳110000)
0 引言
各类高速、大型旋转机械广泛应用于航空航天、能源动力、石油化工等重要工业领域,其性能好坏对于国民经济的健康和国家的安全具有很大的影响。由于旋转机械减振需要,往往将鼠笼式弹性支承与滚动轴承组合使用。带有支承结构件的转子系统是旋转机械的主要组成部分,带有组合支承结构的转子系统是一个内部各个组件强耦合的复杂非线性系统,其非线性振动特性与转子系统运行稳定性密切相关。一方面,这种常见的组合支承结构对于旋转机械的动态特性影响极大,另一方面,由于转子和组合支承结构相互作用,发生非线性振动的转子本身也会在运行过程中改变组合支承结构的动态性能,转子系统的动态特性也会影响组合支承工作性能。因此,为了能对航空发动机转子系统的振动特性进行预测和优化,有必要研究带有组合支承的航空发动机转子系统的非线性振动特性,这对于旋转机械综合性能的提高具有一定的作用。
本文以两支点的鼠笼式弹性支承-圆柱滚子轴承-刚性转子系统为研究对象,充分考虑弹性支承径向刚度、滚动轴承内部非线性赫兹接触力、保持架运动能量和转子动态特性之间的耦合作用,基于能量法建立鼠笼式弹性支承-滚动轴承-刚性转子系统动态特性分析模型,采用数值积分方法对该分析模型进行求解,分析和总结了转子系统不平衡对组合支承力学特性的影响,为采用能量法分析鼠笼式弹支-滚动轴承-转子系统力学特性积累了经验,揭示了在具有强非线性特征的组合支承的激励下,轴承内圈与转子振动呈现丰富的多状态转变现象,在组合支承优化设计时应充分考虑其非线性激励特性对转子系统的影响。
1 组合支承-刚性转子系统数学模型
1.1 组合支承-转子系统构造介绍
典型的鼠笼式弹性支承-圆柱滚子轴承-转子系统结构如图1所示。O为转子几何中心,O1为转子质心,e为转子质量偏心距,转子由鼠笼式弹性支承和滚动轴承组合结构支承,对其结构进行动力学分析可以得到带有组合支承结构的转子系统动力学方程。
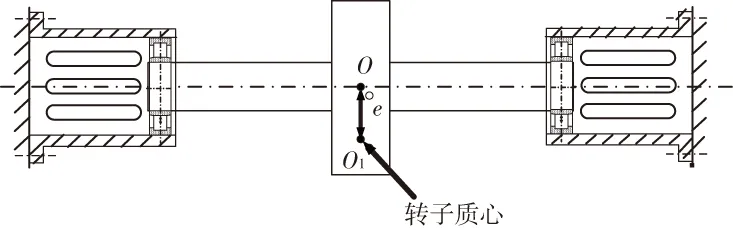
图1 鼠笼式弹性支承-圆柱滚子轴承-转子系统结构示意图
1.2 组合支承力学模型
如图2,鼠笼式弹性支承内部安装滚动轴承以支承转子,鼠笼式弹性支承固定在静止的底座上。根据文献[1],由于鼠笼和轴承的参振质量相比于鼠笼刚度和轴承刚度都很小,因此可以将滚动轴承和鼠笼式弹性支承的组合结构看做是两个弹簧串联。
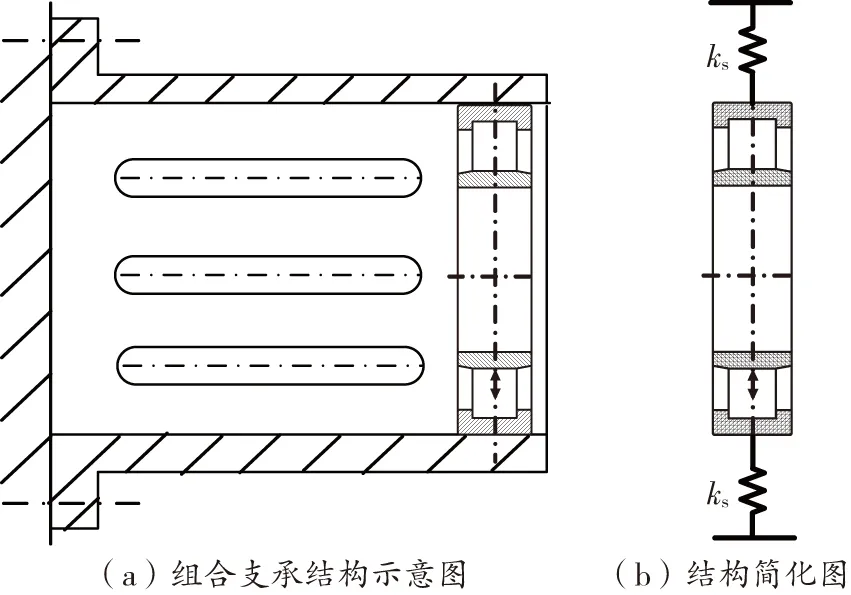
图2 鼠笼式弹性支承和滚动轴承组合支承结构示意图
针对鼠笼式弹性支承的刚度和强度,采用文献中的计算方法,综合考虑鼠笼条长度、宽度、厚度以及数目,可计算得到鼠笼径向刚度K,具体如下[2]:
(1)
式中:E为鼠笼弹性模量;N为鼠笼笼条数量;b为笼条宽度;h为笼条厚度;L为笼条长度。
根据圆柱滚子轴承的结构组成,结合其内部各个部件的相互作用关系,将滚珠和轴承内外圈间的相互作用简化成弹簧-阻尼单元,结合能量法推导得到圆柱滚子轴承各个部件的动力学方程,圆柱滚子轴承的结构简化模型见图3。
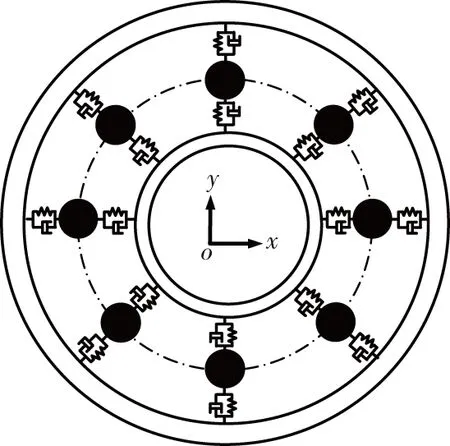
图3 圆柱滚子轴承简化模型
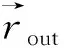
为使用能量法对组合支承-转子系统进行动力学建模,首先需要分析组合支承内部各元件的能量,具体分析过程如下:
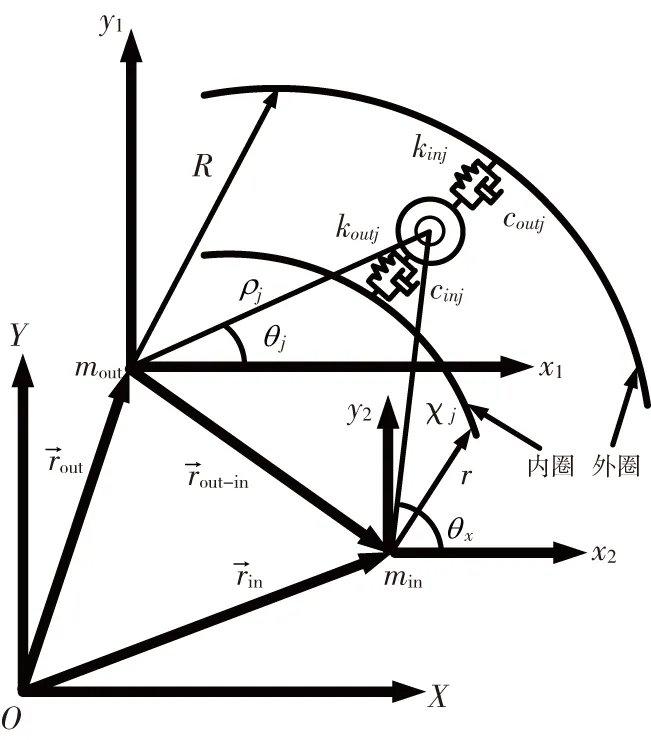
图4 圆柱滚子轴承受力分析模型
1)内圈的能量
(2)
Vin=mingyin
(3)

2)外圈的能量
(4)
Vin=moutgyout
(5)
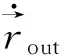
3)滚珠的能量
(6)
(7)

4)保持架的能量
(8)
Vc=mcgyin
(9)

5)轴承内部非线性弹簧的能量
(10)
式中,leff为线接触处的接触长度;δin、δout分别为滚子与内圈和外圈接触变形处简化成的弹簧的变形量。
6)鼠笼式弹性支承的能量
(11)
式中,ks为鼠笼式弹性支承径向静刚度;(xout,yout)为圆柱滚子轴承内圈、外圈质心坐标。
7)转轴的能量
(12)
Vrotor=mrotorgyin
(13)
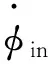
1.3 系统动力学方程
取广义坐标{p}={ρ1,ρ2,ρ3,…,pNb,xin,yin,xout,yout},结合上面所给出的组合支承-圆柱滚子轴承各个部件的能量表达式,根据拉格朗日方程:
(14)
利用拉格朗日方程可以得到组合支承的各个部件的动力学方程:
1)滚子的动力学方程
(15)
2)内圈的动力学方程
(16)
(17)
3)外圈的动力学方程
(18)
(19)
2 系统振动响应分析
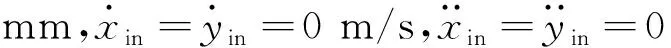
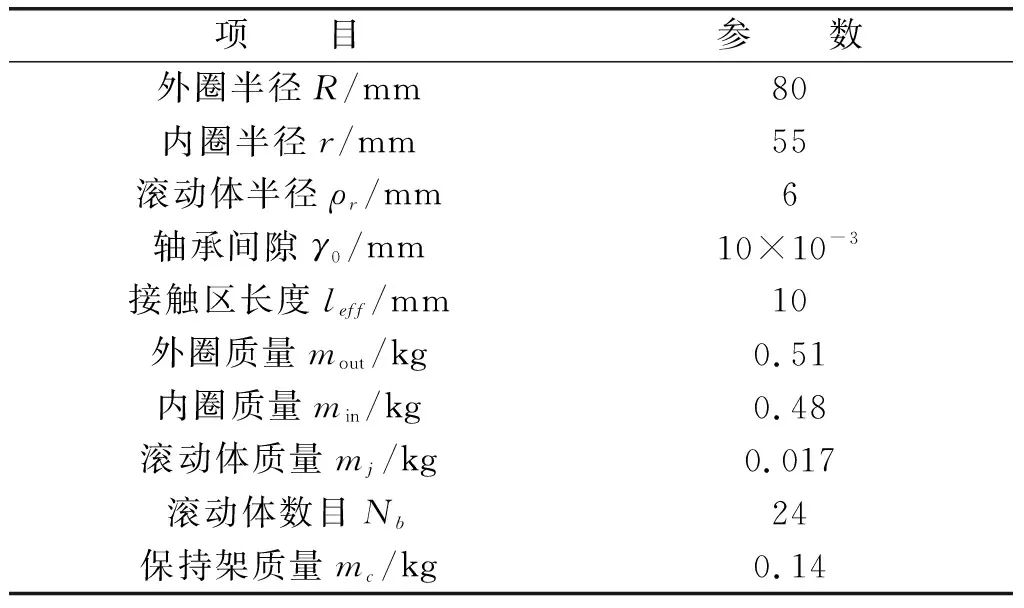
表1 轴承参数

表2 转子参数

表3 鼠笼弹支参数
如图5所示,从分岔图可以看出此转速区间的转子共经历14个阶段:多周期→混沌→多周期→混沌→多周期→混沌→多周期→混沌→多周期→混沌→多周期→混沌→多周期→混沌,为不稳定运动状态。如图,选取代表此转速区间的460 r/min和550 r/min进行仿真,通过仿真结果知道,当内圈转速为460 r/min或者550 r/min时,对应位移时域响应波形没有出现周期性的重复,对应相图不是一个封闭的轨迹,结合其相图和位移时域响应波形,可知转子x方向做混沌运动。
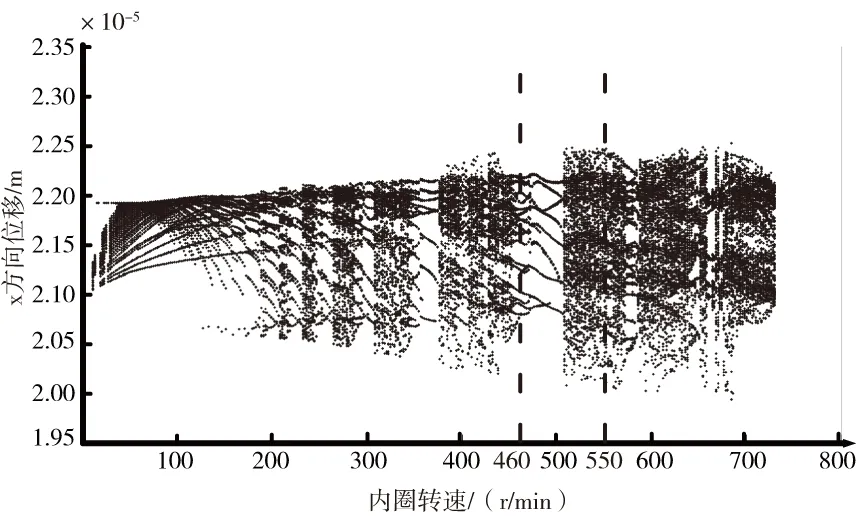
图5 转速 [0,730]区间上位移响应随时间变化的分岔图
如图6,选取此转速区间内460 r/min的情况研究,其位移时域响应和位移响应相图都表现出多周期运动的特征。

图6 转速为460 r/min时内圈位移响应
如图7,选取此转速区间内550 r/min的情况研究,其位移时域响应和位移响应相图都表现出混沌运动的特征。

图7 转速为550 r/min时内圈位移响应
选取高转速[3100,3590]r/min区间进行求解分析,其位移分岔图如图8所示,从分岔图看出,此转速区间对应的内圈x方向运动以多周期运动、一周期运动、两周期运动为主,同时也包含少量的混沌运动和拟周期运动。从分岔图可以看出此转速区间的转子共经历7个阶段:①多周期→②多周期、拟周期和混沌交替出现→③多周期→④多周期→⑤一周期→⑥两周期→⑦一周期,为不稳定运动状态。
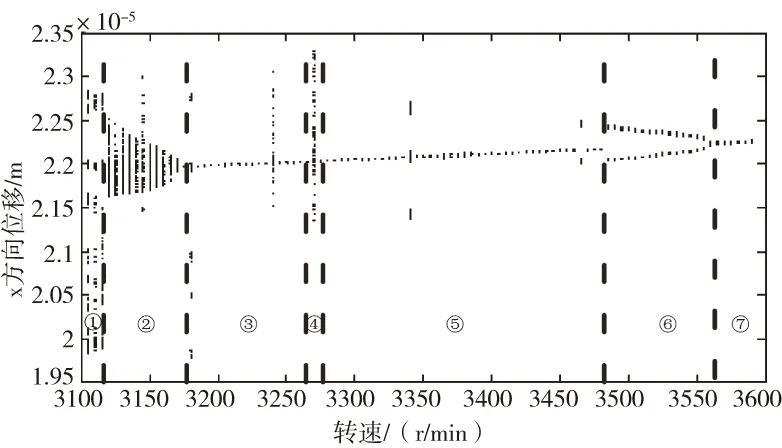
图8 转速[3100,3600]区间上位移响应随时间变化的分岔图
如图9,选取分岔图上对应运动状态为多周期运动的转速区间内的转速为3100 r/min的情况研究,其位移时域响应和位移响应相图都表现出多周期运动的特征。

图9 转速为3100 r/min时内圈位移响应
如图10,选取此转速区间内3125 r/min的情况研究,其位移时域响应和位移响应相图都表现出周期运动的特征。
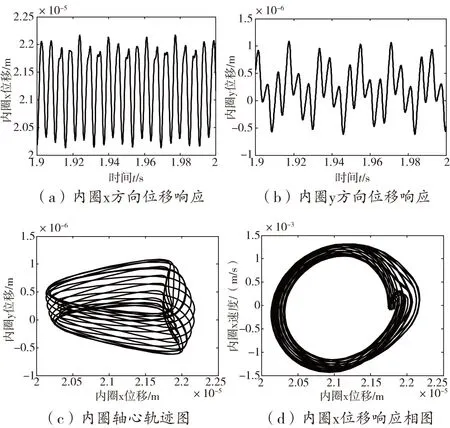
图10 转速为3125 r/min时内圈位移响应
如图11,选取此转速区间内3160 r/min的情况研究,其位移时域响应和位移响应相图都表现出多周期运动的特征。

图11 转速为3160 r/min时内圈位移响应
如图12,选取此转速区间内3300 r/min的情况研究,其位移时域响应和位移响应相图都表现出一周期运动的特征。
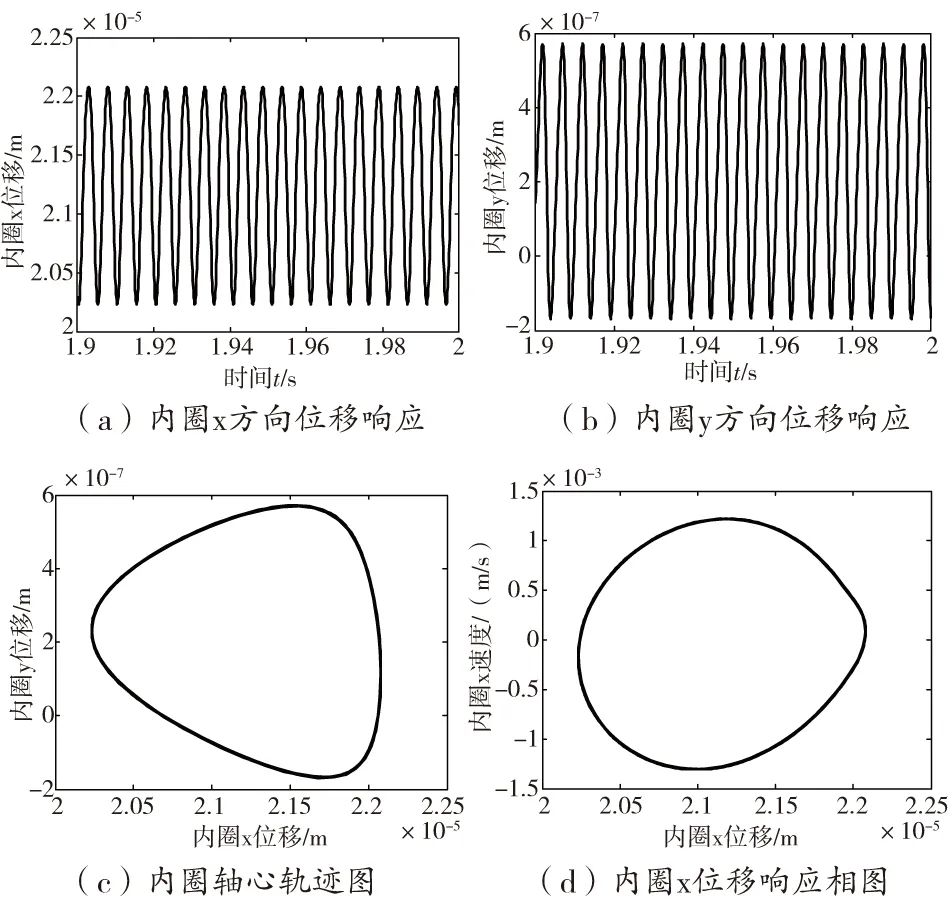
图12 转速为3300 r/min时内圈位移响应
如图13,选取此转速区间内3500 r/min的情况研究,其位移时域响应和位移响应相图都表现出两周期运动的特征。

图13 转速为3500r/min时内圈位移响应
3 研究结论
本文充分考虑轴承非线性支承力、鼠笼刚度以及转子不平衡之间的力学耦合关系,基于拉格朗日能量法,对组合支承-转子系统进行了不同转速区域的振动响应特性分析,从仿真结果来看,可得到如下规律:
1)转子系统的圆盘、轴的振动状态并非与转速等工况参数呈完全正相关或者负相关的关系,在不同的工况参数的范围,转子系统往往呈现不同的振动状态。对比考虑定刚度支承的转子系统和考虑非线性刚度的转子系统,可以知道,这种在不同参数范围的振动状态的变化主要跟支承刚度的非线性有关系。由于支承刚度呈非线性,在不同工况参数下转子系统的振动状态表现非常丰富,在不同参数范围的振动状态的变化规律与非线性系统的特点、支承的刚度特点有重要关系。
2)转速较大时,对应的不平衡激励力也较大,会造成非线性系统的响应出现与不平衡激励较为相似的波动规律,此时非线性支承力对系统响应的影响变小,说明随着转速增加,具有线性特性的不平衡力逐渐增加,而非线性支承力对系统振动的影响逐渐减弱,故系统在高转速区间,往往更多呈现为多周期或者单周期运动。
3)结合上述结论可进一步推断,在低转速区间,鼠笼式弹支-滚动轴承-转子振动响应更容易出现较强的非线性振动规律,甚至出现混沌现象,而高转速区间,该系统非线性振动逐渐减弱,给系统结构设计的启示为:低转速区间应多关注系统复杂的非线性振动规律,采用非线性振动的方法来抑制系统振动或运动失稳,高转速区间应更多关注转子不平衡带来的振幅超限问题,可以近似采用线性振动的理论来对系统进行建模分析以及优化设计。

