核阀流体动力学及流固耦合特性数值模拟

冷 冰，赵 晶

（沈阳工业大学 机械工程学院，沈阳 110870）

0 引言

闸阀以其低流动阻力、低启闭力以及高可靠性等优点，被广泛应用于工业生产，特别是在核电站系统中［1］。作为核电站系统中的重要设备［2］，核电闸阀常用于接通或截断管道中的介质。当核电闸阀全开或全关时，由于高压流体的作用，核阀结构将产生变形及应力［3］。因此，为避免闸阀全开时其结构变形或受力超出许用值导致结构破坏，需对闸阀内部的流场和流固耦合作用下的结构场进行计算分析。

随着计算机技术和数值模拟技术的飞速发展，计算流体动力学（CFD）以其成本低、周期短、结果准确等优点被广泛应用于研究工程流体流动现象。在阀门的流动特性研究中，如球形止回阀的流固耦合特性研究［4］，柱塞泵进排液阀的流场特性分析［5］以及基于动网格的液压滑阀流固耦合分析［6］等均采用CFD数值模拟计算并验证了该方法的可靠性。因此，本文基于ANSYS Workbench有限元分析软件，采用CFX模块对闸阀内部流场进行分析，运用有限体积法（FVM）将闸阀与流场进行流固耦合力学分析，得出闸阀内部流场的压力、速度分布，以及闸阀的变形和应力分布情况，为高压条件下核电闸阀的设计、改进提供可靠依据。

1 流固耦合求解方法

流固耦合是指固体在流体载荷作用下会产生变形或运动，而变形或运动的固体同样会对流体的流场特性产生影响，即流固两相介质之间的相互作用［7］。由于闸阀开启时其结构变形小，对流体流动状态影响较小，因此本研究只考虑流体对闸阀结构的影响，即单向流固耦合作用。

对于流固耦合问题，可通过建立流固耦合控制方程进行求解。流体流动的过程遵循物理守恒定律，即流体控制方程是基于质量、动量和能量守恒定律建立方程；固体结构的控制方程可根据牛顿第二定律导出；基于流体与固体在热流量q、应力τ、位移d、温度T等多个变量的守恒建立以下流固耦合交界面处的控制方程［8-12］：

2 稳态流固耦合分析

2.1 稳态流体动力学分析

2.1.1 网格划分

采用ANSYS Workbench平台中的CFX对流体域采用非结构性网格划分［13］，尺寸函数采用“Curvature”，最大面尺寸设置为2 mm。划分后得到网格单元数为608 083，节点数为121 625。图1示出闸阀流体域网格划分。

图1 闸阀流体域网格划分示意Fig.1 Schematic diagram of fluid domain meshing of the gate valve

2.1.2 边界条件设置

根据设计要求，入口边界条件设置为压力入口，对流体（液态水）入口施加17.2 MPa的压力及350 ℃的温度值，同时启用热能传递模型；出口边界条件设置为速度出口，且出口平面法向速度大小为10 m/s；对称截面上设置对称边界；流体壁面边界条件采用无滑移光滑壁面，忽略与闸阀壁面的热交换影响。图2示出流体边界条件。

图2 流体边界条件设置示意Fig.2 Schematic diagram of fluid boundary conditions setting

2.1.3 结果与分析

图3和4分别示出设计工况下闸阀内流体对称面上的压力分布云图和速度分布矢量。

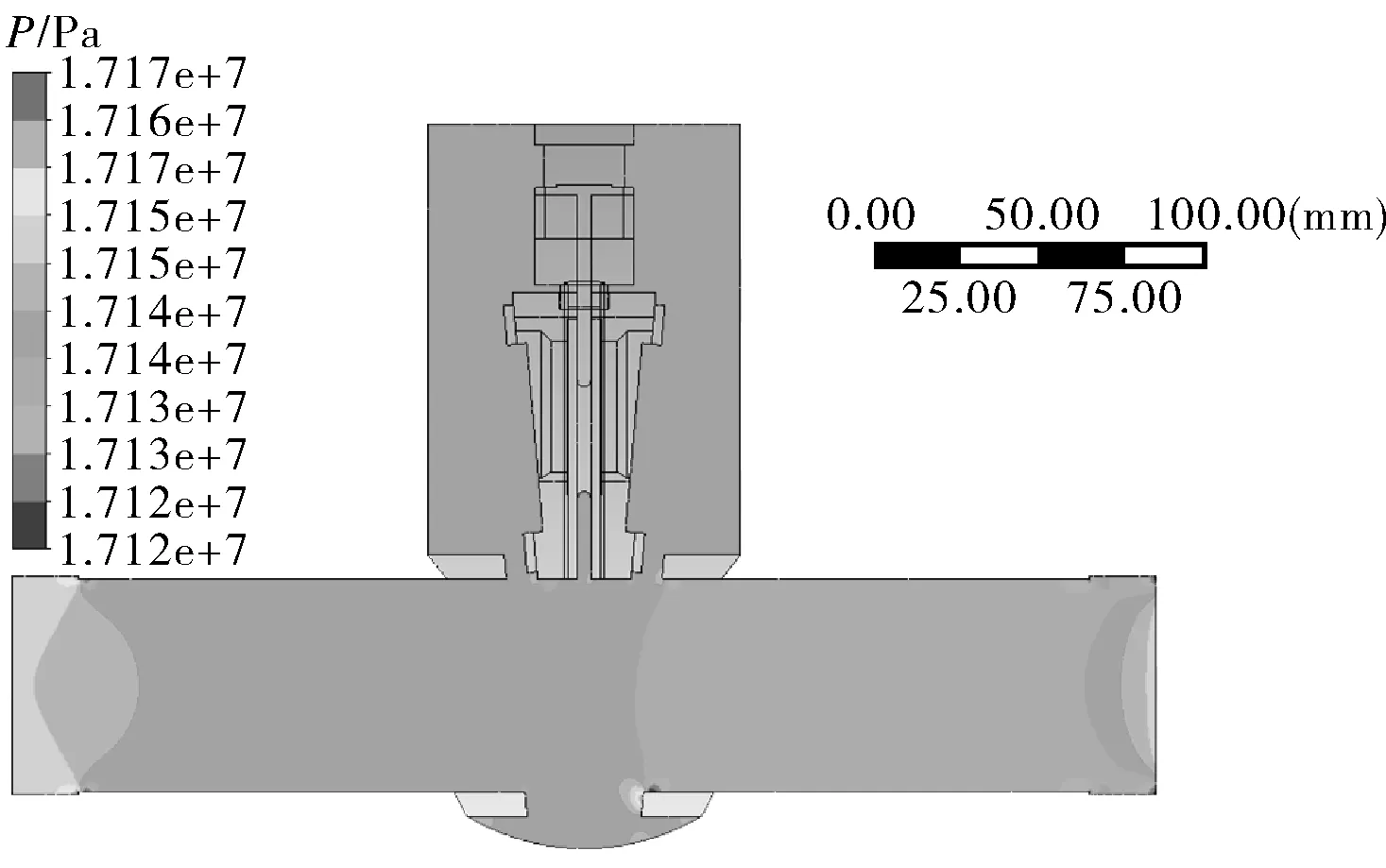
图3 流体对称面的压力分布云图Fig.3 Pressure distribution nephogram of the fluid symmetry plane

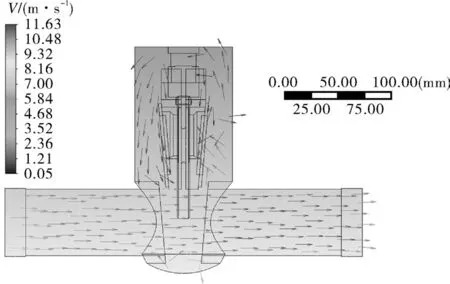
图4 流体对称面的速度分布矢量Fig.4 Velocity distribution vector diagram of the fluid symmetry plane

由图可知，闸阀内流体在流动过程中沿主流通道压力值明显降低，速度值明显增加，这是由于流体在流经阀体中腔时因压力波动在阀体底部产生涡流，导致流体的压力能与动能发生转化。闸阀内流体整体的压力与速度波动较小。

为进一步定量研究闸阀内部的压力及速度变化，分别提取了流动过程中入口和出口平面的平均压力和平均速度。由图5可知，入口和出口平面的平均压力分别为17.15，17.14 MPa，出入口压差数值非常小，仅为0.01 MPa。由图6可知，入口和出口的平均速度分别为9.99，10.08 m/s，速度有所增加，但增加幅度较小，仅为0.9%。

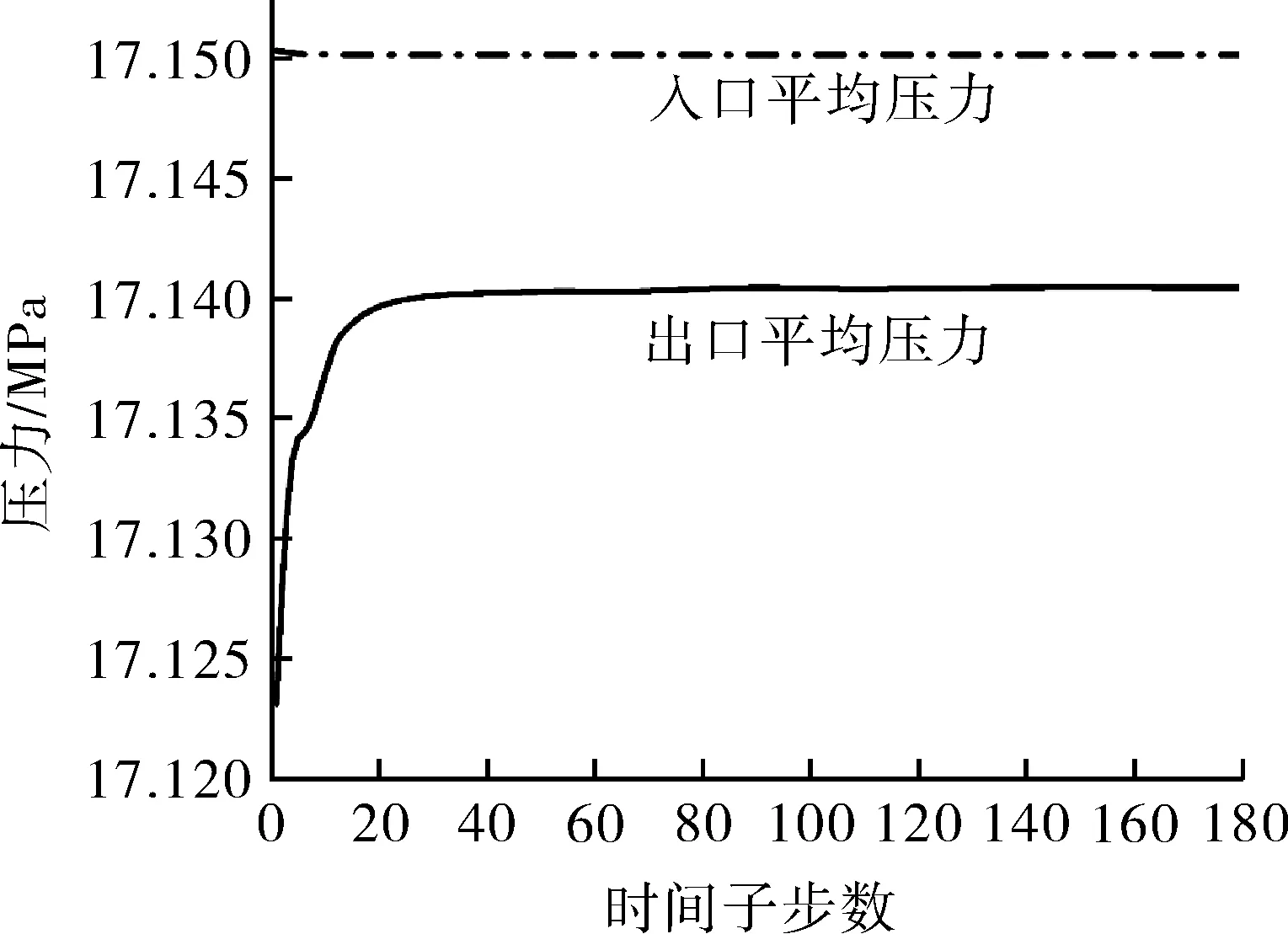
图5 稳态模拟过程中出入口平均压力变化曲线Fig.5 Variation curves of average pressure at inlet and outlet during the steady-state simulation

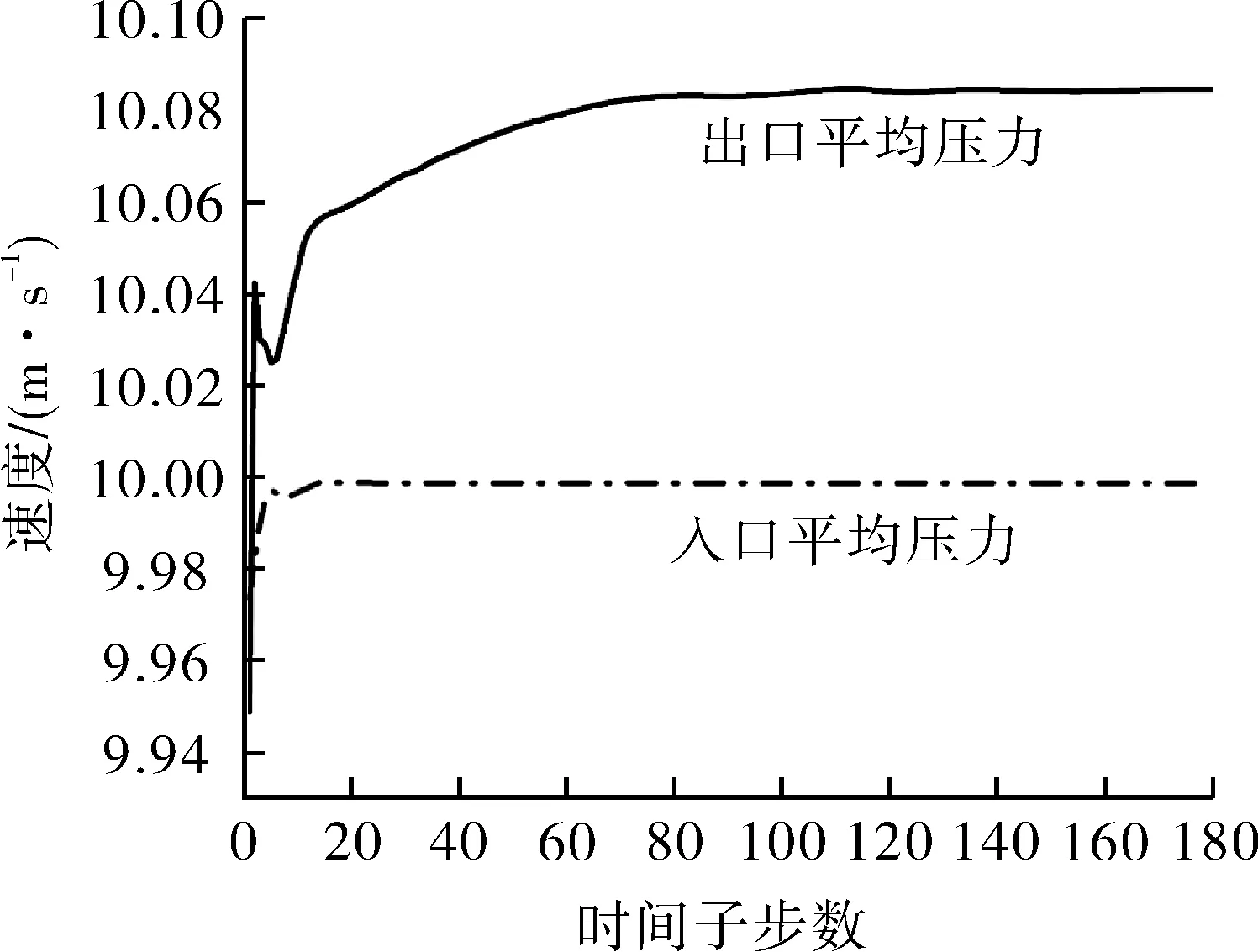
图6 稳态模拟过程中出入口平均速度变化曲线Fig.6 Variation curves of average velocity at inlet and outlet during the steady-state simulation

2.2 稳态流固耦合静力学分析

2.2.1 材料属性设置及网格划分

闸阀结构及部件材料属性分别如图7及表1所示。为提升模拟效率，闸阀结构采用非结构网格划分，尺寸函数选择“Curvature”，最大面尺寸设置为4 mm，划分后得到网格单元数为189 100，节点数为420 667。图8示出闸阀固体域网格划分。

表1 闸阀各部件材料参数Tab.1 Material parameters of components of the gate valve

图7 闸阀结构示意Fig.7 Schematic diagram of the gate valve structure

图8 闸阀固体域网格划分示意Fig.8 Schematic diagram of solid domain meshing of the gate valve

2.2.2 施加载荷及约束

流固耦合过程中闸阀内壁受到的力是由流体压力引起，因此，将2.1节中稳态流动模拟得到的流体压力施加在闸阀内壁，如图9所示。根据闸阀各零部件的装配约束关系，对闸阀入口和出口面、阀体上表面以及阀盖上表面施加固定约束。

图9 闸阀固体域导入压力载荷示意Fig.9 Schematic diagram of the imported pressure load in the solid domain of the gate valve

2.2.3 结果与分析

根据GB/T13927-1992规定，在试验过程中，为避免壳体因受力变形过大出现渗漏现象，通常把承压边界（阀体）的变形控制在0.001DN的范围内。阀体公称直径为130 mm，即允许变形量为0.13 mm。

由图10闸阀变形分布云图可知，受到稳态流体压力冲击后，闸阀变形主要集中在阀体与导轨，最大变形量为0.025 mm，而闸板变形量次之，最大值为0.02 mm，闸阀其余部位受流体冲击较小，其变形量非常小，均在0.01 mm以下。由图11闸阀等效应力分布云图可知，在稳态流固耦合作用下，闸阀应力主要集中在阀体的左右侧壁及底部处，最大等效应力为98.46 MPa，闸阀其余部位受流体冲击较小，其等效应力值较小，均小于材料的许用应力。

图10 闸阀变形分布云图Fig.10 Deformation distribution nephogram of the gate valve

图11 闸阀等效应力分布云图Fig.11 Equivalent stress distribution nephogram of the gate valve

3 瞬态流固耦合分析

3.1 瞬态流体动力学分析

在实际工程中，由于物体运动、边界条件改变或流动自身特性等原因，流动现象会随着时间变化而变化。因此，设定瞬态模拟来研究流体动力学及流固耦合现象是非常有必要的。

3.1.1 模拟设置

瞬态分析的初始值表示瞬态现象在0时刻的物理状态，是流体内部自发的瞬态现象。为保证瞬态计算结果的准确性，通常以一个收敛的稳态分析结果作为相应瞬态分析的初始值。因此，以2.1节中稳态流体动力学求解结果作为瞬态模拟的初始值，对瞬态模型进行如下设置：分析类型为无耦合瞬态（Transient）模拟，总时间为0.1 s，时间步长为0.000 5 s。

3.1.2 结果与分析

为研究瞬态模拟过程中流体压力和速度的变化情况，分别提取 0.025，0.050，0.075，0.100 s这 4组不同时刻的压力分布云图和速度分布矢量图。如图12，13所示，在瞬态模拟过程中，压力在初始时刻入口处最大，由于压力能与动能的转化，沿主流通道出现压力下降、速度增加的趋势，二者的整体波动幅度均较小。此外，由于阀体底部出现涡流现象，压力在流出时变得不均匀，从而导致出口面中间压力大于周边压力的现象。

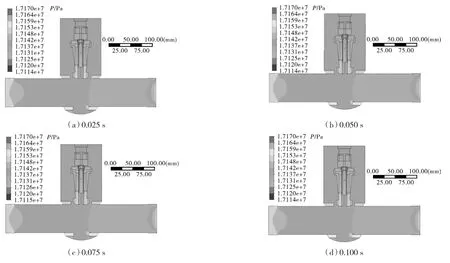
图12 瞬态模拟过程中对称面不同时刻压力分布云图Fig.12 Pressure distribution nephograms of the symmetry plane at different moments in the transient

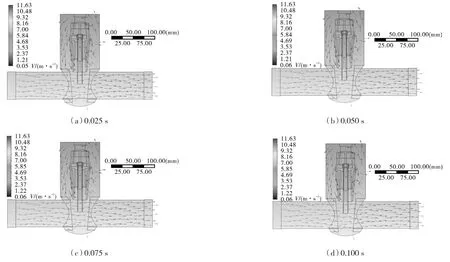
图13 瞬态模拟过程中对称面不同时刻速度分布矢量图Fig.13 Velocity distribution vector diagrams of the symmetry plane at different moments in the transient simulation

3.2 瞬态流固耦合动力学分析

3.2.1 模拟设置

为研究流体瞬态特性对闸阀变形与受力情况的影响，分别导入 4组（t=0.025，0.050，0.075，0.1 s）与瞬态流体动力学分析相一致的瞬态模拟压力，且4组导入压力的加载方式设置如下：“Initial Time Stepping” 设 为 2.5e-4，“Minimum Time Step”设为 2.5e-5，“Maximum Time Step”设为2.5e-3。

3.2.2 结果与分析

由图14闸阀变形分布云图可知，在4组不同时刻瞬态模拟的分析结果中，闸阀变形均集中在阀体、阀体上的导轨以及闸板处，其中导轨、闸板处变形量均在0.1 s时最大，分别为0.101 mm和0.016 7 mm。闸阀其余部位受流体冲击较小，其变形量较小，均在0.01 mm以下。

由图15闸阀等效应力分布图可知，闸阀应力分布主要集中在阀体和出入口阀座处，其中在0.1 s时阀体等效应力值最大，为259.69 MPa，超过阀体材料的屈服强度，产生局部应力集中。根据图14的闸阀变形计算结果可知，阀体在0.1 s时的最大变形量为0.101 mm，小于其允许变形量0.13 mm，阀体压力边界完整性保持良好，满足工程使用性能要求。可通过在应力集中部位加大圆角以减小应力集中程度。

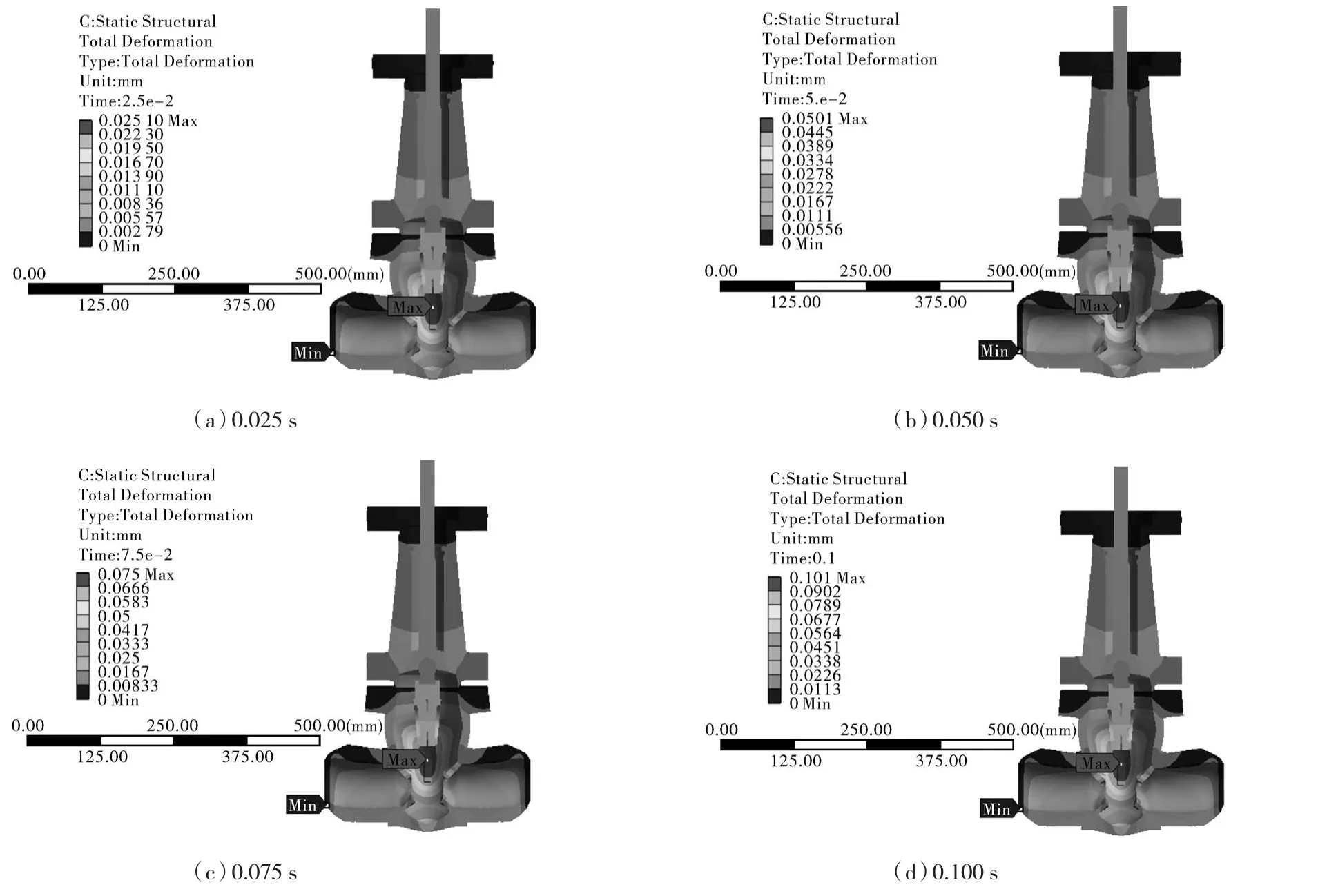
图14 不同时刻闸阀变形分布云图Fig.14 Deformation distribution nephograms of the gate valve at different moments

图15 不同时刻闸阀等效应力分布云图Fig.15 Equivalent stress distribution nephograms of the gate valve at different moments

4 结论

（1）在稳态、瞬态流场特性模拟过程中，由于阀体底部的结构变化，流体在流经此处时均会因压力波动而产生涡流，出入口压力损失均较小，通过改进阀体底部结构可进一步减小压力损失。

（2）在稳态流固耦合模拟过程中，闸阀变形主要集中在阀体与导轨部位，且最大变形量远小于阀体的允许变形量0.13 mm。其次，闸阀在各个部位的应力值均小于其材料的许用应力，在实际工程应用中可满足强度要求。

（3）在瞬态流固耦合模拟过程中，闸阀的最大变形与最大等效应力均出现在阀体与导轨部位，最大变形量为0.101 mm，小于其允许变形量，阀体的压力边界完整性保持良好；最大等效应力略大于材料的屈服强度，产生局部应力集中。可通过加大阀体与导轨部位的圆角以减小应力集中的程度。