水轮机模式液力透平叶片进口安放角影响分析

陈金保 ，肖志怀 ，2，李延频 ，胡 晓 ，刘 东 ，张利红

（1.武汉大学 动力与机械学院，武汉 430072；2.武汉大学 水力机械过渡过程教育部重点实验室，武汉 430072；3.华北水利水电大学 乌拉尔学院，郑州 450045；4.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；5.华北水利水电大学 水利学院，郑州 450045）

0 引言

我国石油化工、海水淡化、钢铁等领域存在大量的余压液体，通常采用结构简单、容易获得的反转泵模式液力透平来加以回收利用［1-2］，但该模式液力透平具有级数多、尺寸大、效率低、高效工作范围窄、稳定性差等缺点，按原动机原理设计的超低比转速水轮机模式液力透平则可以解决反转泵模式结构上的问题［3-6］。超低比转速水轮机模式液力透平的转轮采用超低比转速混流式，单级转轮可以承担更高压头，其液力透平可以极大减少级数，从而达到结构简化、效率增加的目的［7-9］。

目前，一些学者采用数值模拟方法对超低比转速水轮机模式液力透平的特性、选型等开展了相关研究。文献［10］研究了水泵水轮机、常规水轮机及超低比转速水轮机3种单级液力透平，结果表明，相同轴面尺寸下，水泵水轮机适用于工业低压流体的能量回收利用，常规水轮机适用于工业中等压流体的能量回收利用，超低比转速水轮机适用于工业高压或超高压流体的能量回收利用。文献［11］研究了二级常规、低比转速及水泵-水轮机3种水轮机模式液力透平对应的转轮，分析3种水轮机模式液力透平转轮的流场特征和工作特性，得出：相同轴面尺寸下，水轮机模式的液力透平扬程更高，为超低比转速液力透平转轮的选型设计提供了参考。文献［12］研究了二级液力透平用级间导叶：同径正反导叶、异径正反导叶和流道式导叶，获得了3种导叶的流场内特性及外特性，为超低比转速水轮机模式液力透平级间导叶型式的选择与流道设计提供了参考；文献［13］研究了水轮机模式液力透平用的蜗壳式进水室、涡室式进水室、环形进水室，通过外特性、内特性分析，获得了各自最优的运行工况和过流能力以及最优效率等，为超低比转速水轮机模式液力透平进水室的选型设计提供了参考。

超低比转速水轮机模式液力透平过流部件选型方面已有研究，但转轮几何参数对超低比转速水轮机模式液力透平性能影响因素大小的研究尚缺乏。转轮是超低比转速水轮机模式液力透平的关键过流部件，其几何参数如：进口直径、出口直径、进口高度、叶片进口安放角等，对液力透平性能有较大影响［14-16］。尤其是转轮进口安放角，直接影响转轮叶片的几何形状，并进一步影响转轮内部水流流态、液力透平水力性能。合理选择转轮进口安放角对液力透平性能的提高具有重大意义，故本文在超低比转速范围（比转速ns小于100 m·kW）内，考虑 β1合理取值范围［17］，以转轮叶片进口安放角 β1=100°，110°，120°的 3 个二级液力透平模型为研究对象，采用FLUENT仿真软件对其不同工况进行定常计算，研究 β1对超低比转速水轮机模式液力透平性能影响规律，为超低比转速水轮机模式液力透平转轮设计提供参考。

1 理论分析

水轮机模式液力透平是按照水轮机的设计理论，同时贯穿水流环量概念，设计出二级透平的各个过流部件（首级导叶、进水室、转轮、级间导叶、出水室）。其中，在转轮设计中有2个假定：水流在转轮进口为无撞击进口，即进口水流的方向与叶片骨线的切线方向一致；转轮出口水流为法向，即转轮出口水流绝对速度的圆周速度分量vu2=0。在这2个假定下，转轮进口水流必须有足够的环量才能把足够的压能转换成相应的旋转机械能。这就是转轮设计中环量的概念所起的作用。

水轮机基本方程式可表示为：

式中 He——水轮机的有效利用扬程；

Hr——水轮机的设计扬程；

η ——水轮机的水力效率；

ω ——转轮角速度；

g ——重力加速度；

C1，C2——转轮进、出口水流环量；

D1，D2——转轮进、出口直径；

vu1，vu2—— 转轮进、出口水流绝对速度的圆周分量。

在法向出口的假设时，可表示为：

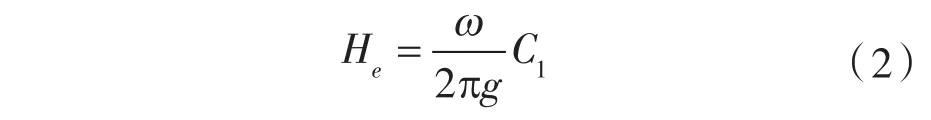
水轮机的基本方程式又可表示为：

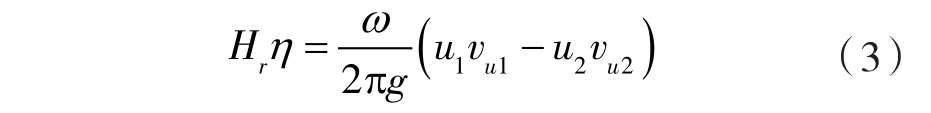
式中 u1，u2——转轮进、出口圆周速度。

在法向出口假设时基本方程式简化为：

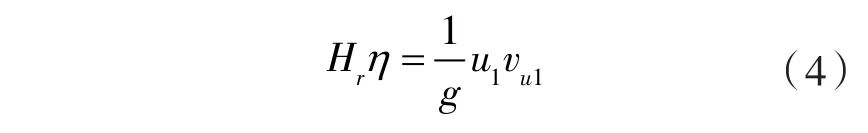
叶片进、出口角的计算是转轮叶片设计的关键。叶片翼型骨线在进水边处的切线与圆周方向的夹角为叶片的进口角 β1，骨线在出口边处的切线与圆周的夹角为叶片的出口角 β2，叶片进、出口角用水轮机速度三角形来确定。水轮机转轮进、出口水流速度三角形如图1所示。

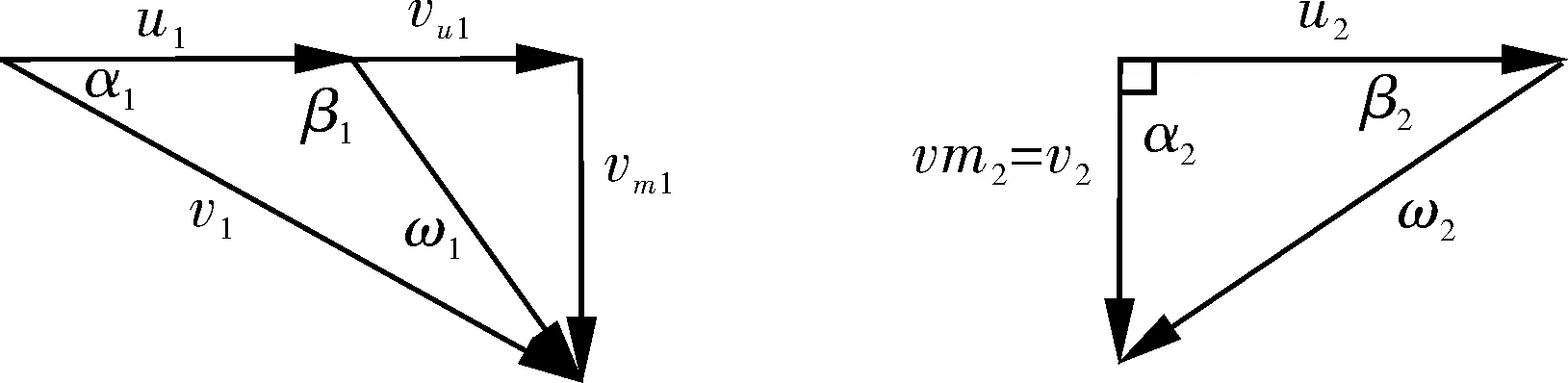
图1 水轮机转轮进、出口水流速度三角形Fig.1 Triangle of water flow velocity at the inlet and outlet of the turbine runner

根据确定的转轮设计参数，由式（5）～（13）计算进、出口速度三角形。

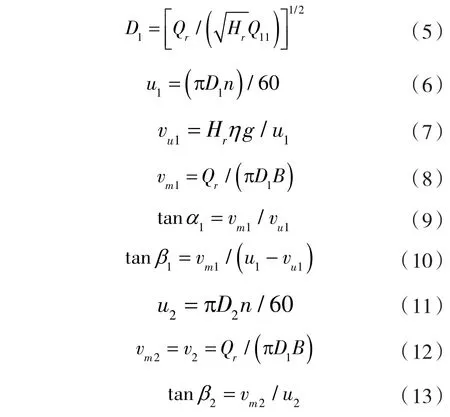
式中 Qr——设计流量；

Q11——单位流量；

n ——转速；

B ——转轮进口高度。

在转轮设计时计算转轮进口速度三角形需要确定3个参数：（1）进口边圆周速度u1；（2）进口水流圆周速度分量vu1；（3）进口边轴面速度vm1。水轮机出口速度三角形的计算在法向出口假定时，出口水流角度α2=90°，只需计算u2与vm2即可，方法同进口速度三角形的计算。

叶片包角与进口角有一定的关系，也会影响液力透平效率、水流流态、压力分布等。进口角小于90°时，叶片包角随着进口角增大而增大；但对于超低比转速水轮机，进口角大于90°时，若仍将进出口间的夹角定义为叶片包角，叶片包角随着进口角的增大而减小。本文研究对象是 β1，为减少叶片包角对探究 β1影响规律的作用，在设计转轮时，当叶片进出口角确定后，进出口用一条光滑的曲线连接。

2 计算模型

为探求不同转轮叶片进口安放角对超低比转速水轮机模式液力透平性能影响规律，需要构建二级液力透平模型。本文采用3个不同 β1的转轮作为对比，基本设计参数见表1，轴面示意如图2所示。其中转轮叶片进口安放角 β1分别为100°，110°，120°，由式（14）计算出其比转速 ns分别为 97.3，96.3，95.2 m·kW。

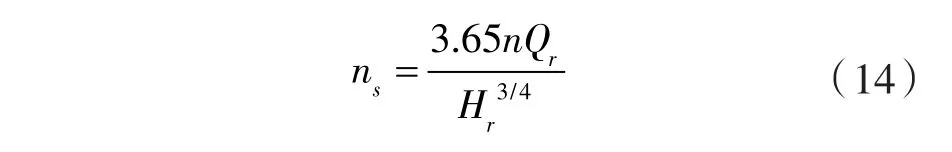
表1 转轮设计参数Tab.1 Design parameters of runner

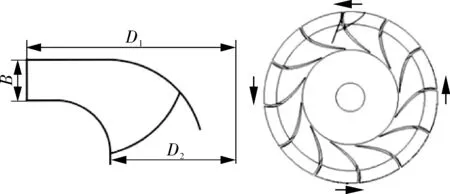
图2 转轮几何参数Fig.2 Geometry parameters of runner

根据表1中的参数，基于混流式水轮机转轮的水力设计方法，采用具有强大三维建模功能的Pro/Engineer软件设计出对应的3种超低比转速转轮，与其它过流部件组合，形成3种不同的液力透平模型。液力透平三维模型如图3所示。

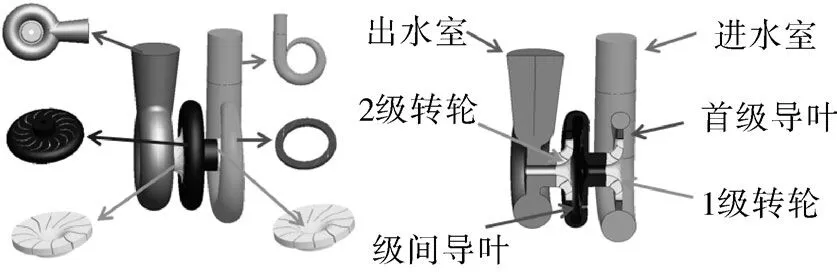
图3 液力透平三维模型Fig.3 Three-dimensional model of T-type hydraulic turbine

3 数值计算

3.1 网格划分

液力透平各部件网格模型如图4所示。

图4 液力透平网格模型Fig.4 Grid model of T-type hydraulic turbine

采用ICEM软件以非结构化网格中八叉树的方法对液力透平三维模型进行网格划分，将几何模型与数值方法连接起来。

3.2 网格数量选择

网格数量较少时对数值计算的结果影响较大，但当网格数量足够多时几乎不再对数值计算结果有所影响。本文采用5种不同数量的网格对β1=100°的液力透平模型进行数值计算，并以额定工况下的扬程、效率作为比较参数。计算结果如图5所示。

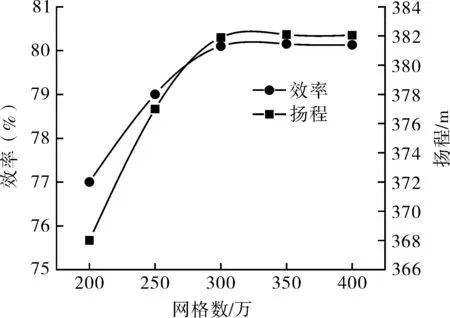
图5 网格无关性验证Fig.5 Grid independence verification

从图5可以看出：随着网格数量的增加，液力透平扬程、效率曲线逐渐升高并趋于平缓，当网格数量达到350万时继续增加网格数量对扬程、效率的影响较小，扬程和效率浮动都在0.3%以内。故本文在各模型网格数量处理上，通过使各模型的网格数量都达到350万来减小网格数量对数值计算结果的影响。

3.3 边界条件与参数计算

FLUENT仿真软件计算前需要设置边界条件。进口条件：垂直蜗壳进口方向设置速度值。根据式（15），β1分别为 100°，110°，120°的 3 个液力透平进口速度 v分别为：13.6，13.9，14.2 m/s。出口条件：出水室出口设为无压出口，即Pout=0 Pa。固壁条件：设定无滑移边界，动静交界面设置为动静耦合面。扬程、效率、出力是液力透平的重要性能指标，计算方法如式（16）～（18）。

进口速度v：

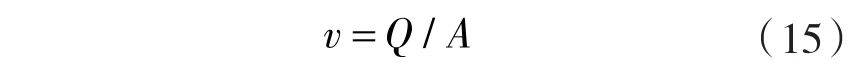
工作扬程H：

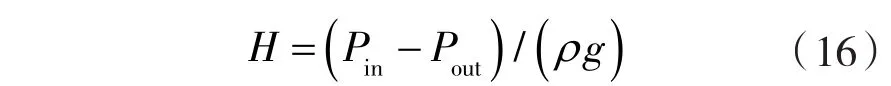
效率η：

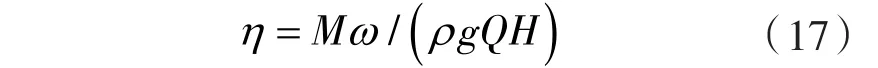
出力P：

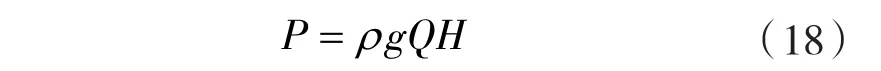
式中 Q ——工作流量；

A ——转轮进口面积；

Pin——蜗壳进口总压；

Pout——尾水管出口总压；

ρ ——液体密度；

M ——轴扭矩；

P ——出力。

4 计算结果分析

4.1 外特性

额定工况点数值模拟计算结果见表2，由表2可以看出：超低比转速水轮机模式液力透平的额定流量Qr随着叶片进口安放角 β1增大而增大，总扬程H与总出力P也随着叶片进口安放角 β1增大而增大，但由于效率的下降，P增大幅度会变小，液力透平的整体水力效率η随着 β1增大而减小；采用超低比转速混流式转轮，超低比转速水轮机模式液力透平能回收更高的扬程［11］，且出力较大，可大大减小液力透平的级数，从而达到简化结构的目的。

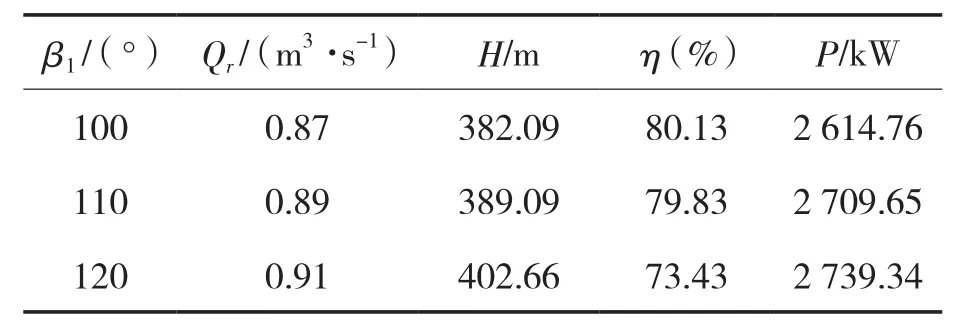
表2 额定工况点计算结果Tab.2 Calculation results of rated operating point

采取 Q 分别为 0.6Qr，0.8Qr，Qr，1.2Qr，1.4Qr，1.6Qr共6个工况进行数值计算，以在多工况下分析比较转轮叶片进口安放角对水轮机模式液力透平性能影响。根据各工况下的数值模拟结果得到超低比转速水轮机模式液力透平扬程、效率与β1关系曲线如图6所示，超低比转速水轮机模式液力透平转轮损失与 β1关系如图7所示。由图6可以看出：在同一流量下，总扬程与叶片的进口安放角 β1有关，扬程随着 β1的增大而增大；液力透平的效率与流量关系η=f（Q）呈抛物线状，且存在最优工况点，偏离最优工况时，液力透平的效率会有所下降；液力透平在不同流量时的效率均与β1有关，β1较小时效率较高，随着β1的增大效率呈下降趋势。由图7可以看出：β1越大，转轮损失越大，且当 β1=120°时，转轮损失增大的较明显；在同一流量下，转轮损失随着β1的增大而增大；随着流量的逐渐增大，转轮损失先减小后增大，且存在最小值。

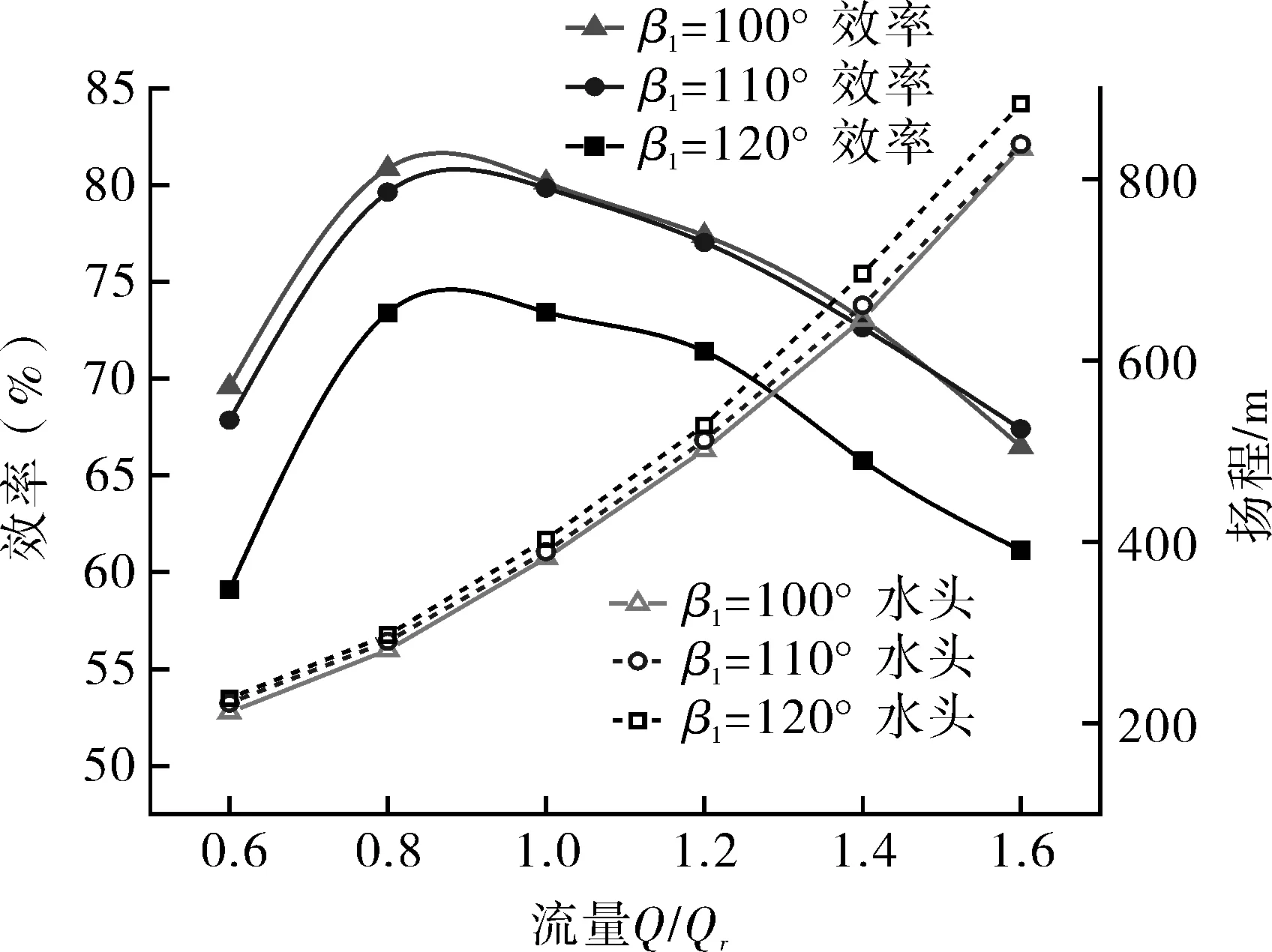
图6 液力透平扬程、效率与 β1的关系曲线Fig.6 Relationship between head， efficiency and β1 of T-type hydraulic turbine

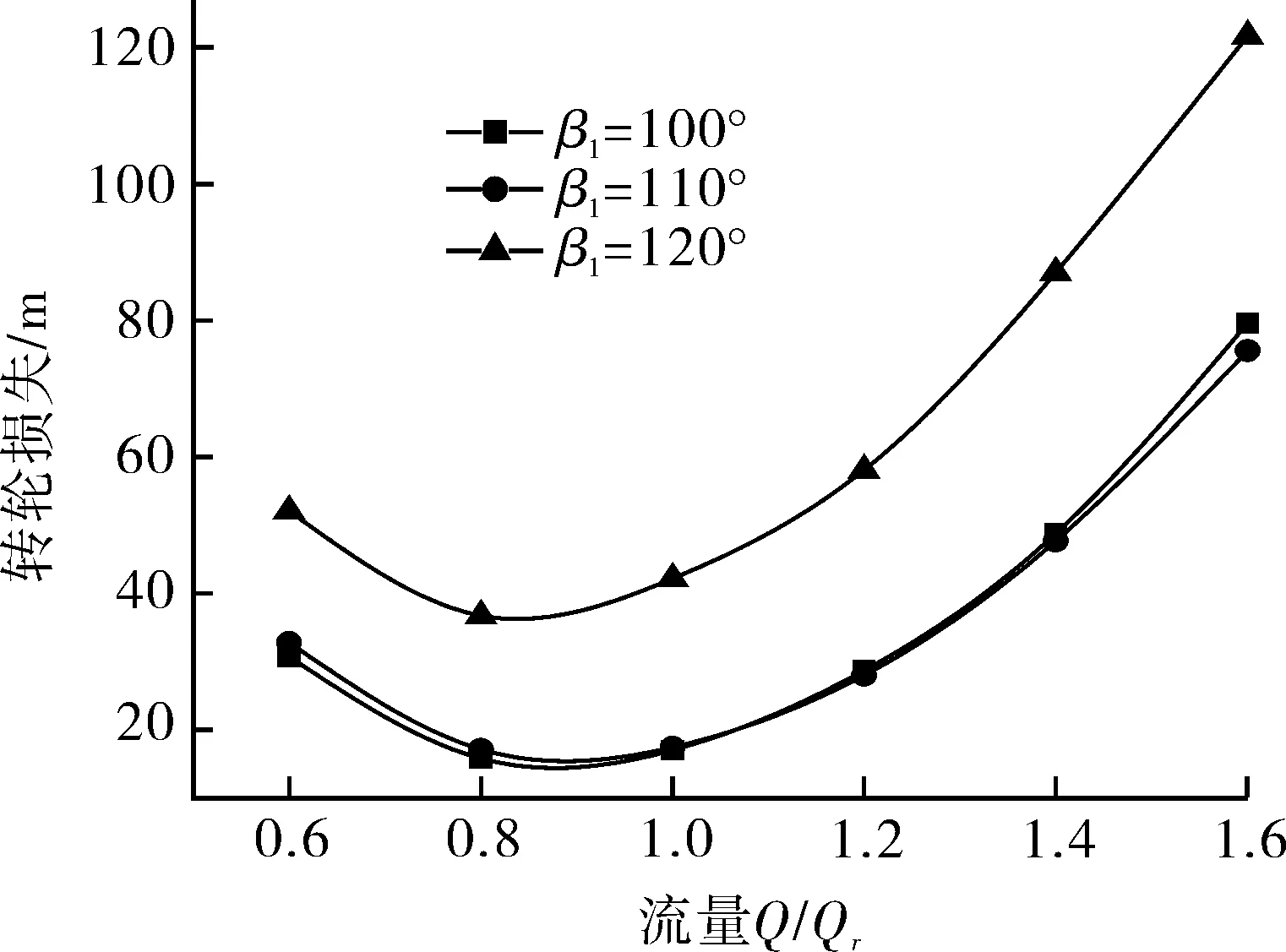
图7 液力透平转轮损失与 β1的关系曲线Fig.7 Relationship between the loss and β1 of runner of T-type hydraulic turbine

4.2 转轮内部流态分析

为研究转轮叶片进口安放角对超低比转速水轮机模式液力透平内流场的影响，本文在设计工况下，分析比较不同叶片进口安放角的转轮内特性。

4.2.1 转轮内部流场分析

根据流场仿真结果取出一级转轮和二级转轮的流线，如图8所示。

图8 3种转轮流线Fig.8 Streamline diagram of three kinds of runner

从图中可以看出，在额定流量时转轮内的流线呈现如下规律：

（1）在叶片进口安放角β1=100°，110°，120°的这3种转轮中，流线分布规律基本相同，一级转轮流态均比二级转轮流态更加平缓。其原因是导叶出口的流态直接影响其后的转轮流态。两转轮前部的导叶不同，首级转轮前是径向式导叶，二级转轮前是具有正反导叶的组合导叶，级间导叶中的水流经180°的急转弯后变得较紊乱，影响了二级转轮中的水流流态。首级导叶、级间导叶流线分布图如图9所示。

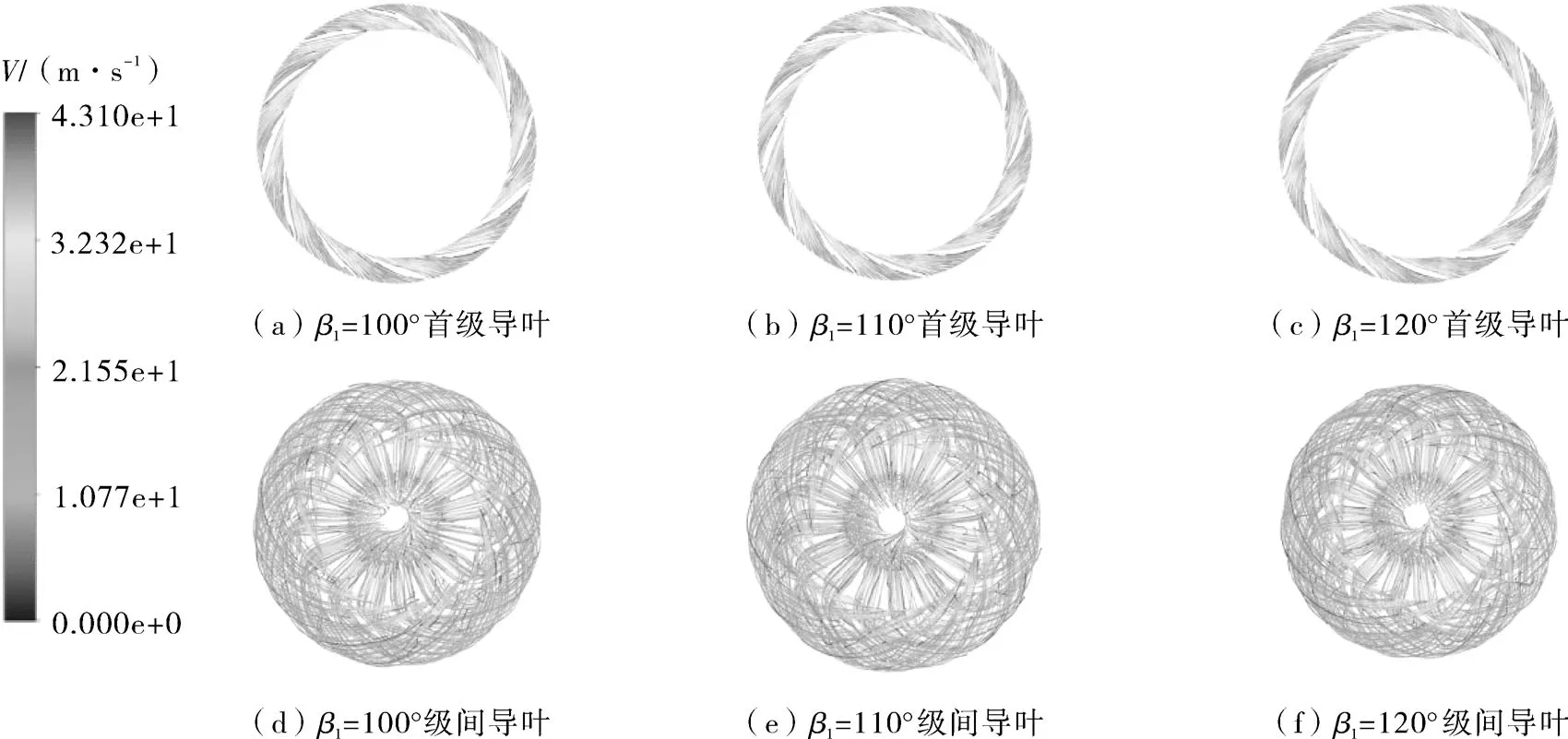
图9 导叶流线Fig.9 Streamline diagram of guide vane

（2）3种不同 β1的转轮的流线分布情况是：叶片进口安放角β1越大，叶片越弯曲，流线越紊乱；β1=120°的转轮流线漩涡最多、最大，β1=100°的转轮流线相对平顺，漩涡也相对较少。

（3）翼间流道流线分布不规则，在叶片正面存在脱流现象。主要原因是水流通过叶片的弯曲处时，速度方向与叶片方向不一致。

4.2.2 转轮叶片压力分布

根据流场仿真结果取出一级转轮叶片和二级转轮叶片的压力云图，如图10所示。

图10 转轮叶片压力分布Fig.10 Pressure distribution of blade of runner

比较3类转轮叶片压力分布，可以得到以下规律：

（1）3种转轮的叶片工作面进口压力总体上大于背面的压力，符合叶片式流体机械的基本规律。

（2）叶片工作面从进口到出口压力均逐渐降低，其背面从叶片内侧到外侧压力逐渐增大。工作面叶片的出口处出现了低压区，面积较小，而叶片的背面靠近叶片内侧和出口处出现了大面积的低压，这是由于超低比转速转轮叶片的弯曲度较大所致。

（3）在叶片背面弯曲度较大的中间处，有部分低压区，这是由于该处水流速度相对较大，也就是水流的动能较大，依据伯努力方程，该处的压力能较小，即易形成低压区。

5 结论

（1）转轮叶片进口安放角 β1是影响超低比转速水轮机模式液力透平性能的关键因素，β1越大，超低比转速水轮机模式液力透平效率越低、扬程越高、出力越大。

（2）当 β1过大时，超低比转速水轮机模式液力透平扬程增大，但转轮损失增大幅度非常明显，严重影响了液力透平回收扬程的效率。

（3）随着 β1的增大，转轮叶片高压区面积增大，转轮内部流体流态变差，直接影响液力透平的水力性能，为了使液力透平回收更多压能的同时具有较高的效率，转轮叶片的进口安放角 β1不宜取值过大。