在培养数学思维点上着力——“平行四边形面积”教学思考与实践

福建省厦门市集美区西亭学校（厦门外国语学校集美分校） 吴娜玲

数学教育要发挥数学培养人的思维能力的作用，由于学生最具有发展潜能，所以教师在传授知识的过程中，需要通过课前的精心构思、课中的巧妙实施、练习的典型设计，调动学生思考的积极性，在培养数学思维点上着力。笔者以人教版五年级下册“平行四边形的面积”为例，借助数学思想方法这条暗线，发展学生思维能力，提高学生数学素养。

一、深入剖析误区，找准思维“落脚点”

“平行四边形的面积”是“多边形的面积”这一单元的入门知识，是学生学习“三角形的面积”和“梯形的面积”的基础，这也是从数格子计算面积到利用转化的思想计算面积的一个关键转折点。本学期的“除数是小数的除法”和“稍复杂的方程”等内容都是利用转化的方法来学习的，但这是数与代数方面的转化，本节课是学生第一次接触空间图形方面的转化思想，对学生来说是陌生的。

（一）课前的思考误区，强硬灌输转化

（二）合理利用数格子，找准“落脚点”

数格子是学生之前计算面积的方法，符合他们的认知学习规律，而转化体现了另一种学习方法，这两种方法并不是冲突、分裂开来的，而是认知过程中的两个水平阶段，是循序渐进的。因此，不要把“数格子”这个过程省掉，相反应该让学生动手操作，留给他们充足的时间来数，通过对以前知识的应用，认识到这个方法的局限性，这样学生就会自然而然地寻求新的学习方法，这时候转化的思想自然顺势而出，不需刻意引导。

二、动手实践操作，突破思维疑难点

数学课堂学习与具体的实践操作活动是分不开的，在课堂教学中重视学生动手操作，是发展学生思维、培养学生数学能力最有效的途径之一。能在课堂教学中适当运用实践操作，让学生动手、动脑，亲身经历与感知学习新知的过程，有助于学生掌握新知识。本节课的教学难点是理解平行四边形面积的推导过程，教学过程中多次运用各种操作方法，帮助学生理解知识，突破思维疑难点。具体操作设计如下。

（一）拉伸平行四边形

在课一开始，直接出示主题图（图1），课件出示学生的争论，通过两种不同形状菜地的对比，引起学生认知冲突，激发学生浓厚的求知欲望：平行四边形的面积怎么求呢？跟长方形一样吗？

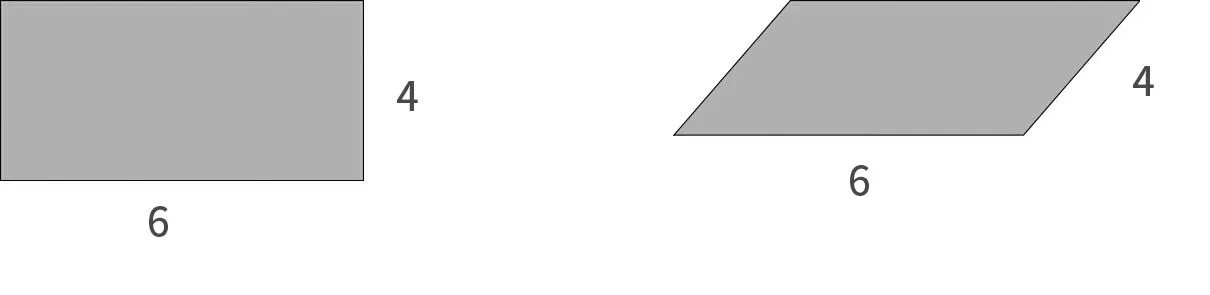
图1

长方形的面积学生都会求，他们看到平行四边形的第一感受也是直接用6×4 计算平行四边形的面积，这时教师出示活动的平行四边形，拉动它的对角，演示从长方形到平行四边形的变化过程，学生很容易发现底和邻边长度不变，但面积却变小了，平行四边形的面积不能用6×4 计算，这个简单的实践操作，学生立刻否定了之前的猜测，平行四边形的面积不能像长方形的面积那样直接计算。同时引发学生思考：平行四边形的面积到底和什么有关？

（二）数格子

本次操作遵循学生的认知特点，从已有的学习经验入手，首先让学生用数格子的方法求出书本80 页两个图形的面积，把平行四边形和长方形的面积填在表格上；接着数出长方形的长与平行四边形的底；最后再数出长方形的宽和平行四边形的高。这样学生在操作过程中慢慢领会到平行四边形与长方形之间有一定的联系，并引起对二者关系的思考：它们之间有什么联系呢？

在数格子的过程中，学生知道了长方形的面积和平行四边形的面积相等，长方形的长和平行四边形的底相等，长方形的宽和平行四边形的高相等。但如果要算一个很大的平行四边形，还利用数格子这样的方法来计算方便吗？很明显这是不现实的，从而让学生感受到数格子方法的局限性，进而引发学生积极探索：如果能像长方形的面积公式那样，找出平行四边形的面积公式就好了。

（三）剪一剪、拼一拼

剪拼是本节课的重要操作，通过剪拼操作帮助学生突破难点。这个环节分为两个层次。第一个层次是积累量化的过程，教师准备了丰富的素材，鼓励学生大胆尝试，想办法找出平行四边形的面积，学生通过多次剪拼，会发现拼组后的图形与原来的平行四边形的面积是相等的，但这时学生的“剪”可能是随意的、不严密的。第二个层次是量变引起质变的过程，教师适时追问：这条线是随意的一条线吗？引导学生继续尝试：沿着哪条线剪会更容易求出面积？为什么要沿着高来剪？（长方形的四个角都是直角，沿着高来剪就可以创造直角）通过这样的追问，引导学生正确地剪、拼，把平行四边形转化成长方形，为后面提炼平行四边形面积公式奠定基础。

三、渗透转化思想，聚焦思维增长点

转化就是把新知识或者是新问题通过一定的方法转化成已经学过的知识或问题，用学生已有的知识经验解决未知的问题。所以，本课要把平行四边形转化成学生已经学过的长方形来帮助理解平行四边形面积公式的由来与运用，通过三个方面聚焦思维增长点，渗透转化思想。

（一）丰富素材中渗透

在课堂上，提供给学生各种形状的平行四边形，丰富素材，让他们大胆尝试，学生思维聚焦到如何转化。有的学生拿剪刀来剪，沿着高剪的学生发现平行四边形的面积跟剪完后拼成的长方形一样，有的学生不是沿着高剪的，他们发现拼成的图形还是不好算出它的面积，这时他们就会慢慢调整自己的剪法，沿着高剪，最后拼成的图形是长方形时，就能利用长方形的面积公式计算出面积了。

（二）在对比中渗透

课件出示平行四边形和拼成的长方形，让学生思考平行四边形的面积与所拼成的长方形有什么关系。学生思维聚焦到对比，通过观察发现两个图形的底边是一样长的，长方形的宽正好是平行四边形的高。为了让学生对这个认知有更深的感悟，请学生拿一个新的平行四边形，用不同颜色水彩笔画出它的高和底并标注。剪拼后，大家仔细观察，发现长方形的长=平行四边形的底，长方形的宽=平行四边形的高，因此，平行四边形的面积=底×高。

（三）巩固练习中渗透

学生在四年级学习画高的时候已经知道底和高必须是相对应的。但课前笔者做此项调查时发现，大部分学生都知道底和高是相对应的关系，却不知道为什么要相对应。为了突破这个难点，笔者设计了一道练习题与学生一起探讨底和高的对应关系。出示图2 这一图形，并提出问题：你能求出平行四边形的面积吗？

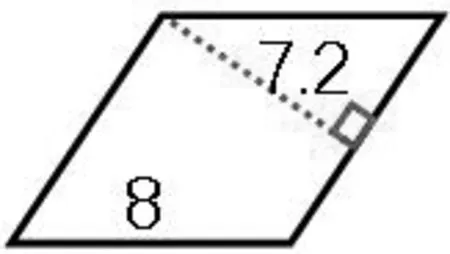
图2

大部分学生立刻回答“不能”，但当教师追问为什么不能时，学生却说不出理由了。练习的设计聚焦学生思维困惑处，为了解答学生的疑问，本环节通过课件演示转化过程：沿着7.2 这条高剪下后拼出长方形，拼出来的长方形宽是7.2，但原来平行四边形的底边8 却“隐藏”在长方形里面，并没有转化成长方形的长，因此这样就不能用7.2×8 算出长方形的面积，也不能求出平行四边形的面积了。通过此次演示，学生对底和高的相对应关系有了更深刻的认知。

学生是一个个鲜活的个体，他们的思维是无限发散的，思想碰撞的火花虽小但却是绚烂的。本节课中多让学生动手操作，在学生自主参与活动的过程中，关注学生的思维能力，多加引导，广开思路，在学习过程中渗透转化思想。只有铭刻在心中的数学思想、数学思维方法，能随时随地发生作用，能使学生终身受益。