考虑休班公平及同班次约束的呼叫中心排班优化问题
胡修武,徐 悦,王秀利
(南京理工大学经济管理学院,江苏南京210094)
1 引 言
呼叫中心(Call Center/Contact Center)是通过电话等电信媒介手段为顾客提供产品售后支持、订购交易等服务的组织实体.呼叫中心属于劳动密集型行业,人力成本占运营成本的70%左右;呼叫中心人力运作管理引起了学术界广泛研究兴趣[1,2].近年来,随着更多制造商专注于核心业务能力提升而愿意把产品售后电话服务外包出去,国内从事呼叫服务业务的呼叫中心企业越来越多,行业规模扩展迅速[3].实际调研发现,呼叫中心企业面临着年轻员工自我意识强、对工作条件及环境要求较高和离职率居高不下等情况.坐席人力排班时,企业除了考虑劳动法规合同要求,越来越注重纳入人性化管理因素来提高员工满意度,从而有助于提升服务效率.
呼叫中心人力运作管理研究大致可分为人力需求计算、路由策略和人力排班.人力需求计算或路由策略研究成果很多,而呼叫中心排班问题研究相对较少[4−7].最近,Defraeyen和van Nieuwenhuyse对呼叫中心排班问题研究成果进行综述[7].一些呼叫中心排班问题研究假设计划周期为日期,考虑日内各种实际场景因素,如坐席人员多技能[8,9]、区段人力需求随机动态性[10]、各班次不同成本及交叉培训成本[11]、或连续区段人力需求关联性[12]等,构建坐席人员排班问题(随机)整数规划模型,并分别提出最优算法以及启发式或智能算法.这些研究因计划周期是日期,不涉及员工休班及不同日期班次关联等决策问题.也有少数学者研究计划周期为单周的呼叫中心排班问题,构建整数规划模型并提出优化算法[13,14].与行业内文献[13,14]不同,本文研究明确纳入了双休日休班公平性考虑,并通过同班次用工约束来保证员工上班规律性.我们注意到,近些年来其它行业(如医疗[15−17]、运输物流[18,19]和零售[20]等)的人力排班研究中,考虑了双休日休班或其它方式的排班公平性.不难看出,呼叫中心行业在用工规定、业务需求分布和人力班次结构等方面与这些行业不同.尽管本文排班问题也同样纳入双休日休班公平性等因素,但呼叫行业本身特点决定了研究模型方法不同于这些行业人力排班问题.
与国外同行业普遍周薪制不同,国内呼叫中心通常实行月薪制,通过编制月度排班表对坐席人力进行计划管理.班表编制时,通过保证双休日休班公平和周内同班次当班来体现企业人性化管理理念.针对该实际排班场景,本文给出了制定排班方案的优化模型和方法,并且量化分析了这些人性化管理因素对人力成本控制的影响.本文创新性体现在两方面,一是通过分析推导,取得了反映排班问题优化规律的一些理论结果;二是在借鉴已有研究成果基础上,通过利用问题本身结构和优化性质,提出了求解排班方案的优化模型和算法.实例计算验证了排班模型和算法的有效性;研究表明在兼顾休班公平性和上班规律性情况下,仍能够对排班人力成本进行有效控制.
2 坐席人员排班模型
研究的排班问题中,假设用工制度除了反映国内劳动法规要求,还包括以下两点体现人性化管理的约束因素.首先,基于生活、社交和子女教育等原因,大多数员工愿意双休日休班.为了照顾员工生活方便性及体现公平性,排班时在班表周期内要保证每个员工双休日休班不少于规定次数.其次,由于坐席人员排班的复杂性,手工排班经常致使周内当班班次不同的员工占比偏高.当班班次频繁切换对员工工作及生活具有很大负面影响.为了保证工作时间规律性,规定每个员工周内工作日同班次当班.
本文排班问题具体描述为,在满足服务水平指标要求和企业用工制度约束情况下,确定连续4周内坐席人员当班与休班日期,以及当班日期班次,使得坐席人员使用数量最少(即优化人力成本).具体说明如下.
呼叫服务系统可用排队论模型来描述,其中假设顾客电话到达率服从泊松分布,坐席人员服务率服从指数分布.服务水平指标通常采用队列中顾客呼入电话在给定等待时间内接通的百分率(Telephone Service Factor,TSF)刻画.给定服务指标TSF,使用排队论方法Erlang C可计算出达到指标TSF需要的最少坐席人员数量[1,2,7].目前,Erlang C 因简单易用,仍然是最为广泛使用的人力需求计算方法.该方法由于没有考虑服务队列中的弃话现象,计算的人力需求往往偏大.若考虑队列弃话现象并假设顾客耐心时间服从指数分布,就是模型Erlang A.很多学者推荐使用Erlang A来计算坐席人力需求[2,7,14].本文采用Erlang A计算坐席人力需求,用计算出的最少坐席人员需求数量来刻画服务指标TSF要求.
企业用工制度既反映国内劳动法规合同要求,也体现企业自身管理偏好.本文假设用工制度包括,S1:员工每周当班天数不应超过5天,每天最多1 个班次当班.S2:员工4 周内至少1 个双休日休班.S3:员工双休日两天要么全当班,要么全休班.S4:员工周内工作日当班班次相同,不同周当班班次可以不同.约束S1反映国内劳动法规对员工休班天数的规定.在4周排班表中,由于每周双休日总需要安排部分员工当班来提供呼入话务服务,尽管大多数员工愿意双休日休班,客观上只能安排部分员工双休日休班.规定S2通过保证每个员工至少1个双休日休班来体现周末休班公平性.规定S3既反映员工双休日完整休班意愿,又方便企业安排更多员工双休日休班.其它行业人力排班研究中也考虑了用工规定S2 和S3(如见综述文献[19]).规定S4保证员工周内上班时间规律性,有助于提升员工服务效率.计划周期假设为4个连续完整周,利用上述排班问题优化解,适当补充改动后很容易获得月度排班优化方案.为了方便问题模型和算法描述,定义的参数与决策变量符号见表1.

表1 参数和决策变量说明Table 1 The description of parameters and decision variables
下面构建坐席人员排班优化问题的整数线性规划模型(ILP1)
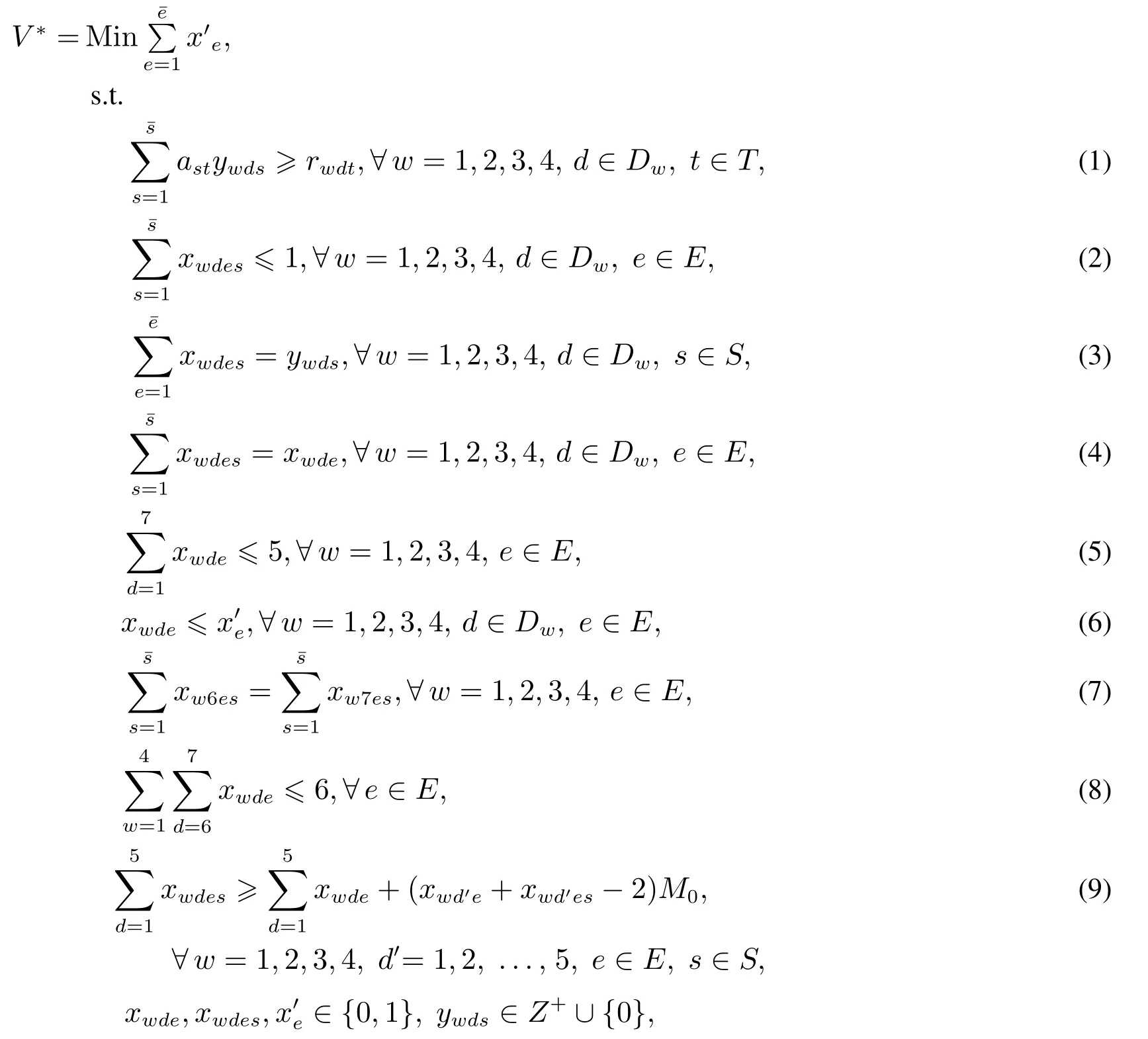
其中式(1)描述达到指标TSF要求的区段当班坐席人力.式(2)表示S1规定的员工每天最多1个班次当班.式(3)和式(4)描述决策变量之间关系.式(5)表示S1规定的员工周内当班天数限制.式(6)表示最优解方案中员工4周内至少当班1天.式(7)表示S3规定的员工双休日要么全休班,要么全当班.式(8)(结合式(7))描述S2规定的4 周内员工至少1个双休日休班.式(9)描述S4规定的员工在周内工作日同班次当班约束,式中M0取充分大正整数.每个员工e在周w内的工作日是否当班和周内当班班次均为决策变量,这意味着规定S4蕴含着可能出现的25|S|种同班次当班情况.对每个员工e,式(9)通过包含的5|S|个具体约束式(s ∈S和d′=1,2,...,5)来刻画所有同班次当班情况.在5|S|个约束式中,至少存在1个式子以条件”某个班次当班天数不少于当班总天数”成立,来保证员工e满足规定S4;而其它式子会因右边第2项取充分小负整数,在逻辑上成立但不起约束作用.反之,如果员工e在周内当班班次不同,则在5|S|个约束式中总存在不能成立的式子.
3 问题分析
本节首先给出人力需求计算方法,然后分析坐席人力需求特征和推导问题优化性质.本文人力需求泛指基于呼入话务量的当班人力需求或纳入用工制度约束后的坐席人员数量需求.
3.1 人力需求计算
呼叫服务系统中,呼入电话到达率或坐席人员处理时间都是随机变量.当话务处理时间相对区段长度较短情况下,则系统在区段内会很快进入稳定状态.在该情况下,可把每个区段的呼叫服务过程看作独立马尔科夫生灭过程(Markovian birth-death process),即满足SIPP(stationary independent period-by-period)条件[1,2,14].若假设日期d内区段t的呼入电话到达率服从数学期望为λtd的泊松分布,std个坐席人员话务处理时间和顾客耐心时间分别服从数学期望为htd(服务率µtd=1/htd)和b的指数分布,则可用排队论模型Erlang A 来近似计算坐席人力需求.
在马尔科夫生灭过程中,令Ptd(n)表示在日期d的区段t内,呼叫服务系统有n个顾客的状态概率,则下列关系式成立,即
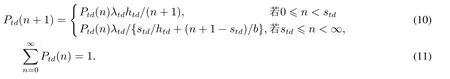
式(10)和式(11)表明,随着n增大,该生灭过程中的电话死亡率会逐渐超过出生率(到达率),从而会导致状态概率以超过几何速度变小.为了能够显式表达状态概率,可在规定误差范围内,忽略高阶状态概率.把顾客等待队列长度限定在上界为N的状态空间内,使得被截去队列长度大于N的状态概率之和不会超过给定误差ε.令ρ=λtd/{std/htd+(N −std)/b},考虑如下关系式
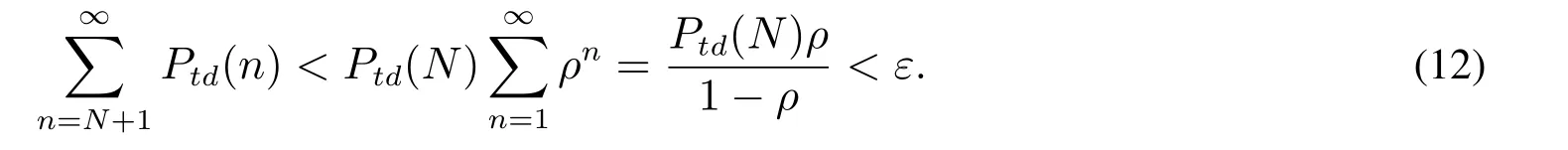
式(12)意味着只要确定充分大N,则能够使得被截去状态概率之和小于ε.确定N后,在队列长度为0至N的状态空间内,可重新归一化计算概率(n),使得
在马尔科夫生灭过程X={X(t)|t0}中,令Pr{W > τ|X=n}表示系统中有n个顾客情况下,顾客等待时长W超过给定时间τ的概率.Pr{W >τ|X=n}可根据下列定理计算.
定理1(见文献[21])在马尔科夫生灭系统中,对任意给定的τ >0,有
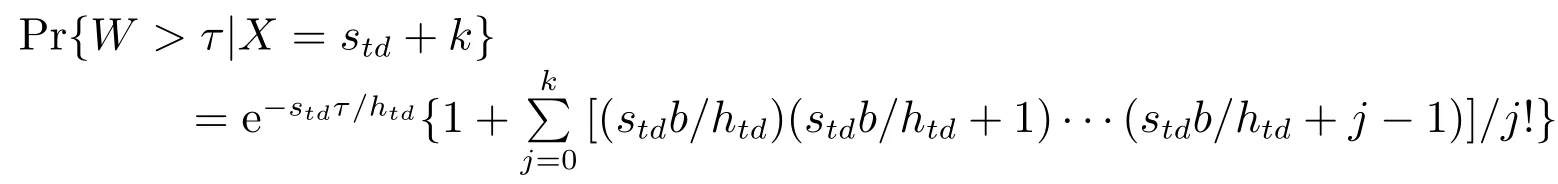
成立.
设Ltd表示日期d内区段t的服务指标TSF,即所有等待顾客在不超过时长τ内接通电话的百分占比.根据以上分析,则有
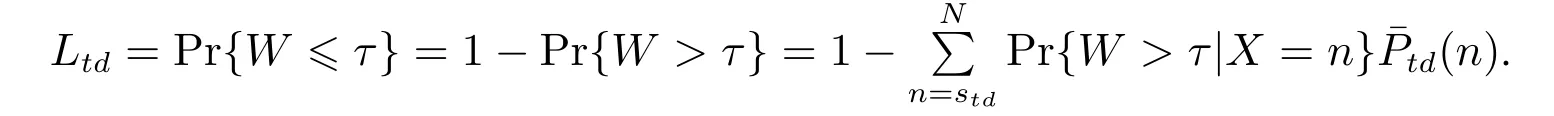
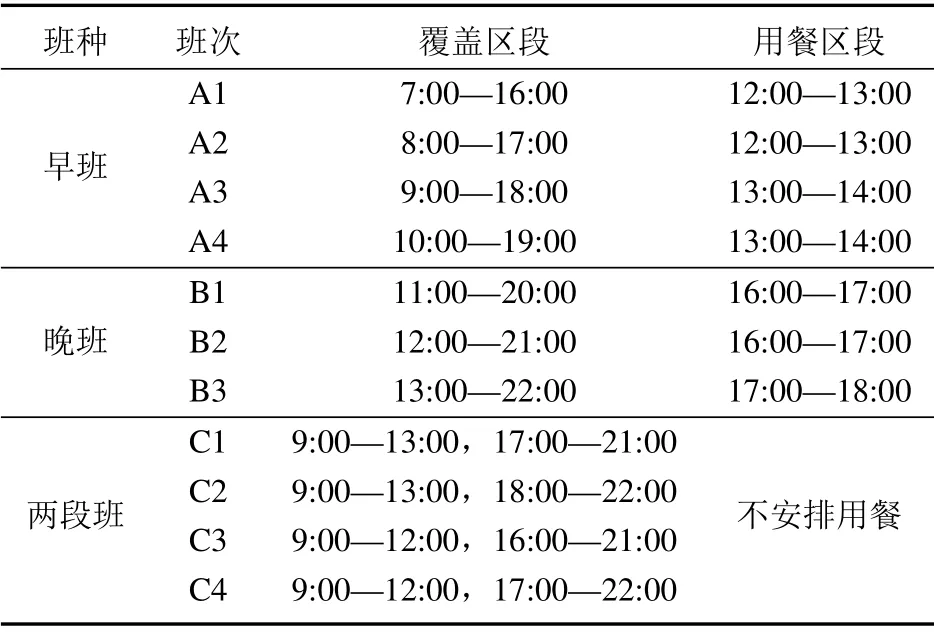
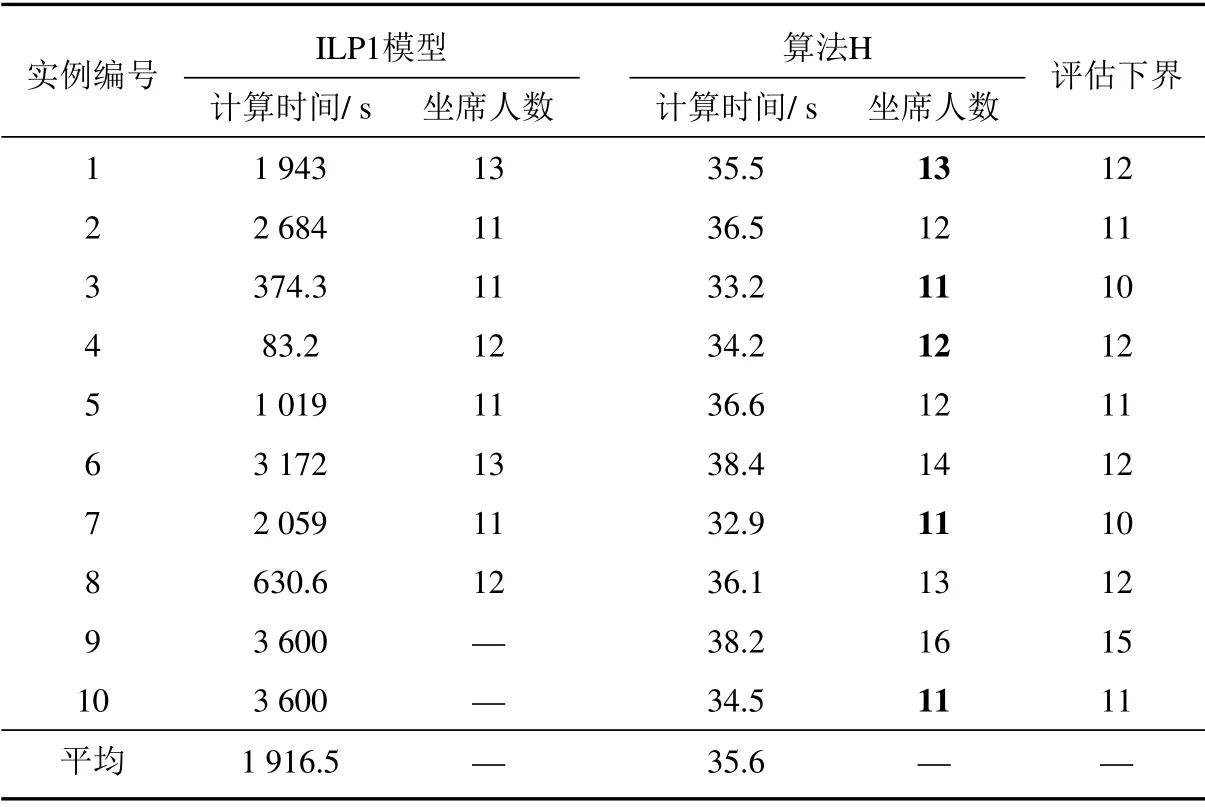
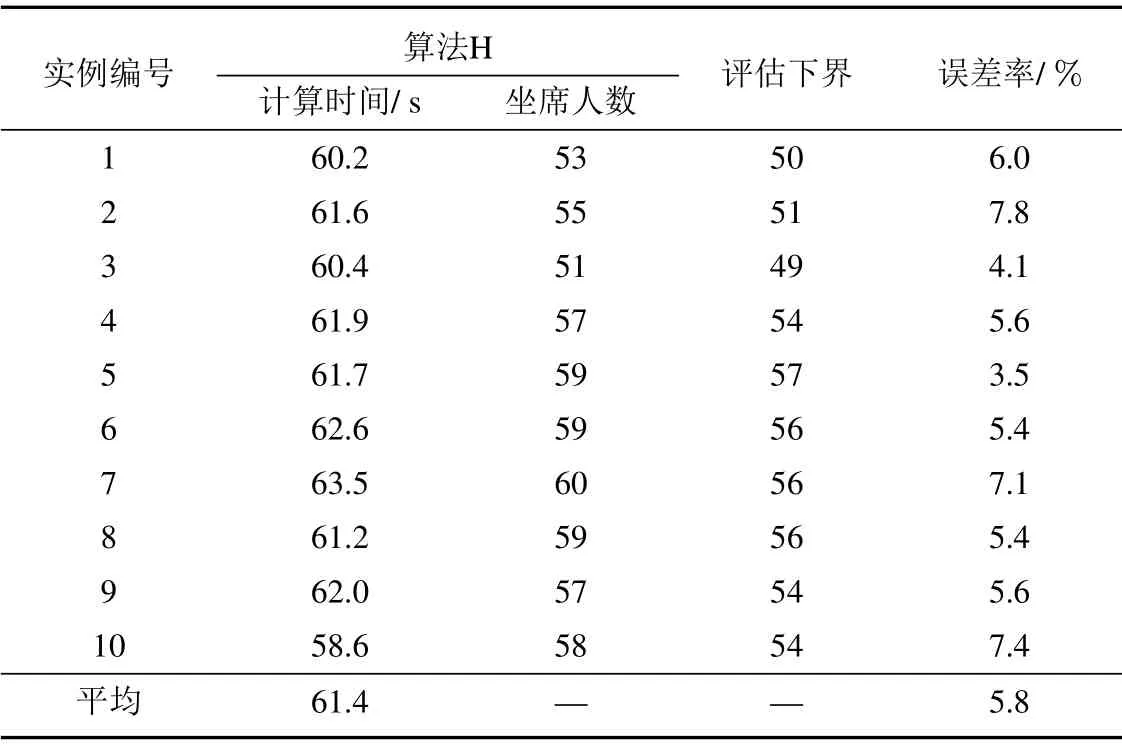
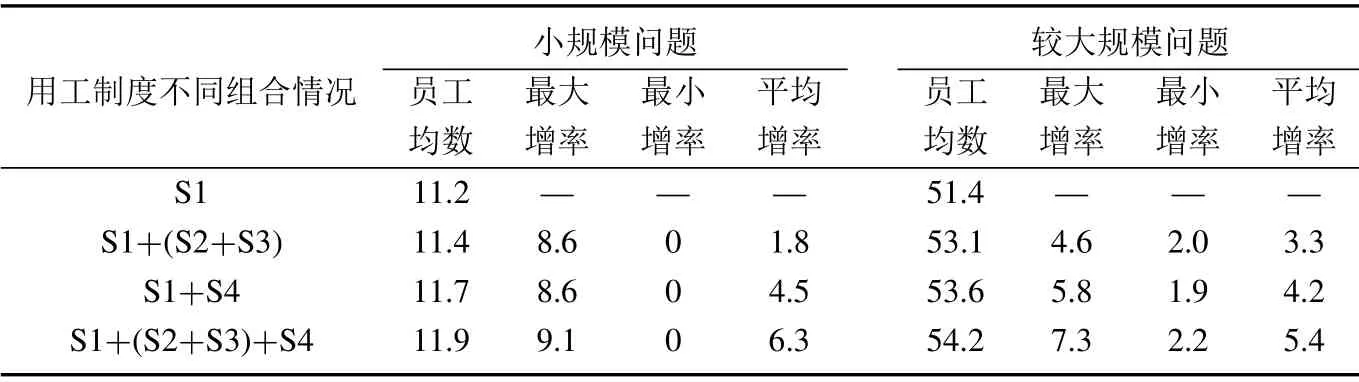
给定TSF指标Ltd,可计算需要最少坐席人员数量rtd如下:初始化,设坐席人员数rtd=和确定状态概率截断误差ε(如10−5),计算出TSF指标L′td.若L′td 由于考虑休班和同班次等用工约束,问题模型ILP1求出的员工数量可能多于班表具体日期内所需要的坐席人力数量.下面首先通过构建整数规划模型界定为了满足话务服务指标要求而每日需要的最少坐席人力,然后通过分析每日最少坐席人力需求与排班周期内用工制度约束之间的关系,推导出问题ILP1下界. 令Q∗wd表示在周w的日期d达到日内话务服务指标要求所需要的最少坐席人力,这里w=1,2,3,4和d=1,2,...,7.给定日内区段人力需求,则Q∗wd可由下列整数规划模型(ILP2)求出,即 令Aw6=Q∗w6和Aw7=Q∗w7.设Aw表示周w双休日需要的最少当班坐席人员数量.考虑用工制度规定S3,则有Aw= max{Aw6,Aw7}.模型ILP2描述的日排班调度问题尽管与问题ILP1不同,但容易看出,模型ILP1最优解方案在周末日期d的排班结果也是该日期模型ILP2的可行解,从这个意义来说,模型ILP2求出的最优员工数量是模型ILP1的下界.进一步分析,根据用工制度规定S2,每个双休日除了要安排一些员工当班来满足日内所有区段人力需求,还可能要安排部分员工休班.同时考虑排班周期内4周双休日当班和休班人力情况,可给出排班问题下界. 引理1问题最优目标值V ∗满足下列条件: 1)V ∗max{A1,A2,A3,A4}; 2)V ∗(A1+A2+A3+A4)/3,这里表示不小于“·”的最小整数. 证明1) 结论显然成立.2) 令uw表示最优解中周w双休日休班坐席人员数量.则对于w= 1,2,3,4,有V ∗Aw+uw成立.故4V ∗(A1+u1)+···+(A4+u4) = (A1+···+A4)+(u1+···+u4)成立.根据用工制度规定S2,则有u1+···+u4V ∗成立.于是有3V ∗A1+···+A4.考虑到V ∗为整数,故结论2)成立.证毕. 若仅考虑每周内具体工作日人力需求,令Bwd表示周w工作日d需要的最少当班坐席人员数量,则Bwd=Q∗wd,这里w= 1,2,3,4 和d= 1,2,...,5.由于规定S1要求每个员工周内双休日或工作日至少休班2 天,同时考虑每周工作日当班和休班人力情况,可导出如下结论. 引理2问题最优目标值V ∗满足下列条件: 1)V ∗max{Bwd|w=1,2,3,4;d=1,2,...,5}; 2)V ∗[2Aw+(Bw1+···+Bw5)]/5,其中w=1,2,3,4. 证明1) 结论显然成立.下面证明结论2).在问题最优解中,令uw和vw分别表示周w双休日或工作日休班的坐席人员数量; 令uwd表示周w工作日d休班的坐席人员数量.对所有日期d= 1,2,...,5,V ∗Bwd+uwd成立.于是,成立.注意到和V ∗Aw+uw,有7V ∗成立.考虑到每个坐席人员周内至少休班2天,且要么在双休日休班,要么在工作日休班,故V ∗uw+vw成立.因此,成立.注意到V ∗,Aw和Bwd均为非负整数,故结论2)成立.证毕. 由模型ILP2求出最优解Aw6,Aw7和Bwd后,这里w= 1,2,3,4 和d= 1,2,...,5,根据引理1和引理2,可确定问题ILP1的下界,记为M. 如果不要求坐席人员周内工作日当值班次相同,即松弛用工制度S4,称之为原问题ILP1的松弛问题.在模型ILP1中,去掉约束条件式(9)后,即为松弛问题整数规划模型描述,记为SILP1.对于松弛问题SILP1,有如下结论. 定理2松弛问题SILP1最优解需要坐席人员数量为M. 证明明显的,松弛问题SILP1的最优解中员工数量不会少于M.若M个员工可生成松弛问题SILP1的一个可行解,则结论成立.具体分析如下. 不失一般性,假设问题ILP1的下界M在第1周取得.考虑下列4种所有可能的情况:i)M=A1; ii)M=1+A2+A3+A4/3;iii)M=B1d,这里d ∈D1和iv)M=[2A1+(B1,1+···+B1,5)]/5. i)当M=A1时 该情况下,可安排所有M个员工在本周双休日当班; 而在其它3周双休日分别安排M −A2,M −A3和M −A4个员工休班.于是,所有员工在4周双休日休班的次数为(M −A2)+(M −A3)+(M −A4)=3M −(A2+A3+A4).由引理1可知,M(A1+A2+A3+A4)/3,注意到M=A1,则有A2+A3+A42M.于是,有(M −A2)+(M −A3)+(M −A4)M.该式意味着能够保证M个员工每人在4周内至少有1 个双休日休班. 由引理2可知,M(2A1+B1,1+···+B1,5)/5.注意到M=A1,于是,有B1,1+···+B1,53M.该情况下,考虑到员工均在本周双休日当班,则本周5个工作日中需要安排2M个休班日期.由于周内工作日需要当班班次总数为B1,1+···+B1,5,而5M −(B1,1+···+B1,5)2M,于是,M个员工每人可在工作日安排至少2天休班.另一方面,安排2M个休班日期之后,员工在周内工作日仍可当值3M个班次.由于本周人力需求B1,1+···+B1,53M,故总可以满足周内工作日人力需求.所以,该情况下M个员工可生成本周内可行解方案. ii)当M=(A1+A2+A3+A4)/3时 该情况下,4周双休日可安排休班员工数依次为M −A1,M −A2,M −A3和M −A4.于是,在双休日休班的员工总数为4M−(A1+A2+A3+A4).考虑到A1+A2+A3+A43M,则4M−(A1+A2+A3+A4)M.该式意味着能够保证M个员工每人至少有1个双休日休班. 该情况下,本周5个工作日中需要安排2A1个休班日期.由引理2可知,M(2A1+B1,1+···+B1,5)/5,即5M −(B1,1+···+B1,5)2A1成立.该式意味着本周5个工作日内可安排另外2A1个日期休班.另一方面,安排2A1个休班日期之后,员工在周内工作日仍可当值5M −2A1个班次.由于本周人力需求B1,1+···+B1,55M −2A1,故总可满足本周内工作日人力需求.所以,M个员工可生成本周内可行解方案. 针对情况iii)和iv),通过与情况ii)相似分析,可以说,M个员工能够生成松弛问题SILP1本周内的可行解方案.对于第2周、第3周或第4周,通过与第1 周情况相似分析,可以断定M个员工能够生成该周内可行解方案.于是,结论成立.证毕. 由引理1和引理2可知,问题ILP1最优解方案至少需要M个坐席人员.由定理2可以推断,若在用工制度S4约束下,M个坐席人员也能生成问题ILP1可行解,则得到其最优解方案.一般情况下用工制度规定S4可能导致问题ILP1需要更多坐席人力. 定理2保证M个坐席人员可生成松弛问题SILP1最优解.不难找出1个问题实例,使得M个坐席人员是问题ILP1的最优解;也就是说,问题ILP1的下界M是最大下界.在问题ILP1 最优解中,有的坐席人员可能不止1个双休日休班.在算法设计中,如果能够合理利用最大下界M,则可以有效避免双休日休班过量指派.M个坐席人员排班需要同时考虑用工制度约束S2和S4;而其它坐席人员均可安排在双休日休班,在工作日当班只要满足约束S4即可. 基于上节分析,启发式算法可采用结构分解技巧.一是基于松弛问题SILP1最优解是问题ILP1最大下界,可把候选坐席人员列表从数量上分为一定或仅可能属于最优解两部分;针对两类坐席人员采用不同指派策略.二是把表征人力需要的待指派班次分为属于双休日或工作日两部分,分别采用不同指派策略.在工作日班次指派中,无论当班日期或班次选择都进行局部优化和体现贪婪搜索思想.提出的启发式算法描述如下. 启发式算法H 步骤1由模型ILP2分别计算问题下界Aw和Bwd;并由引理1和引理2确定最大下界M.设定坐席人员列表集E1={1,2,...,M}. 步骤2对E1中员工进行双休日班次指派.对w= 1,2,3,4,设mw=M −Aw和¯mw= ¯mw−1+mw,这里=0.对w=1,2,3,4,依次进行下列操作: 2–1 设k0=0和b0=0.确定kw和bw,使得¯mw=kwM+bw成立,这里0bw 2–2 在模型ILP2分别求出的周六和周日最优解中,针对个相同当班班次(即满足x∗w6es=x∗w7es=1)需求,把E1中未安排休班的个员工指派到这些双休日班次当班. 2–3 对Aw6−个其它当班班次,把E1中尚未指派的Aw6−个员工指派到周六这些班次当班;对Aw7−个其它当班班次,把E1中尚未指派的Aw7−˜个员工指派到周日这些班次当班. 2–4 若Aw6 步骤3对w=1,2,3,4,把E1分为E′w={iw,1,iw,2,...,iw,M−Aw}和E′′w={iw,M−Aw+1,iw,M−Aw+2,...,iw,M}两个子集,其中,E′w中员工在本周双休日休班,而E′′w中员工双休日当班.设Uw=(rwdt)5ׯt为周w工作日区段人力需求矩阵;对工作日d=1,2,...,5,设Uwd=(rwd1,rwd2,...,rwd¯t)T为周w日期d的区段人力需求向量. 步骤4对w=1,2,3,4,就E′w和E′′w中员工工作日进行班次指派.对员工e=iw,1,iw,2,...,iw,M−Aw和员工e=iw,M−Aw+1,iw,M−Aw+2,...,iw,M,依次进行下列操作: 4–1 在Uw中选择区段(d′,t′),使得rwd′t′=max{rwdt|t ∈T,d=1,2,...,5}成立;若有多个t′使得rwd′t′相同,则选择使集{rwdt′|d=1,2,...,5}含正整数元素最多的区段(d′,t′); 4–2 若e ∈E′w,则令当班日期集D′w=Dw{6,7},转入步骤4–3;若e ∈E′′w,则确定当班日期集如下: 4–3 设˜S={si|si ∈S,asit′=1}和={rwdt1,rwdt2,...,rwdtc}表示由Uwd中c个最大值组成的子集.对每个si ∈和d ∈D′w,定义指标ζw(si,d)={rwdt|asit=1,rwdt ∈,rwdt >0}为班次si覆盖中非零元素的子集. 4–5 对所有d ∈D′w和班次覆盖区段t,如果rwdt >0,则令rwdt ←rwdt−1;使用新rwdt更新替换Uw和Uwd中相应位置元素. 4–6 当Uw >0时,区分以下情况:i)若e=iw,k且k 当Uw=0时,则令E′w和E′′w中e之后的所有员工在本周工作日休班;若存在下个周w使得Uw>0成立,则令e ←iw+1,1,转入步骤4–1;否则,则由E1中坐席人员已生成解方案,结束. 步骤5设e=M+1和E2={e},进行下列操作: 5–1 对所有的Uw1,...,Uwh >0,安排员工e在这些周的双休日休班,并通过与步骤4–1至步骤4–5 相似的操作,把员工e指派到这些周工作日当班;同时,对其它满足Uw=0 的周,安排员工e该周内休班. 5–2 若存在至少1个周使得Uw >0成立,则令e ←e+1和E2=E2∪{e},转向步骤5–1;否则,则由E1∪E2中坐席人员已生成解方案,结束. 在假设工作区段数¯t和班次数¯s给定情况下,排班问题规模可用人力需求输入参数 来刻画.容易看出,步骤4的每个员工指派过程中,至少存在1个周,使得该周工作日当班班次至少覆盖1个区段的有效人力需求(即指派后该区段剩余人力需求满足rwdt −10);另一方面,每个员工4 周内当班/休班指派的计算时间不会超过O(max{4×52×,4×5ׯs}),其中大括号内前项计算确定员工当班日期(步骤4–1 和步骤4–2),而后项确定当班班次(步骤4–3和步骤4–4).考虑到¯t和¯s是问题常数,所以说,步骤4 的计算时间为O(rsum).相似分析可推断步骤5的计算时间也不超过O(rsum).另外,其它步骤2和步骤3计算时间并不占优.因此,在步骤1 使用模型ILP2求出最大下界M之后,算法H中步骤2 至步骤5 的计算时间复杂度为O(rsum). 在算法H中,步骤2在每个周w双休日总是指派Aw个坐席人员当班.无论周六或周日需要当班员工数不会超过Aw,因此,生成解能够满足双休日人力需求.在每个周w的工作日,步骤4至步骤5依次把坐席人员指派到具体班次当班,直至周内工作日区段人力需求Uw= (rwdt)5ׯt被满足.所以,生成解也能满足工作日人力需求. 由引理1和引理2可知,问题最少需要M个坐席人员在4周计划周期内当班.从步骤2至步骤4 可以看出,对集E′w中M个坐席人员,每周有M −Aw个人至少在双休日休班,而Aw个人至少在工作日休班2天.若生成解中还有另外|E2|个坐席人员当班,由步骤5可知,这|E2|个坐席人员至少会在周内双休日休班.所以,生成解能够满足用工制度约束S1. 在步骤2的2–1中,每周指派M −Aw个不同坐席人员双休日休班,4周共指派4M −(A1+A2+A3+A4)个双休班.由引理1 的2)可知,4M −(A1+A2+A3+A4)M.进一步分析步骤2–1可知:指派始于第1周的情况i)k1=k0= 0,对所有情况i)ki=ki−1= 0 指派后,必然出现情况iii)kw=kw−1+1 = 1的指派.当该情况出现时,由于=M+bw=+mwM和< M,则bwmw.于是,在该情况下对坐席人员Aw+1,Aw+2,...,M的休班指派必然覆盖坐席人员bw−1+1,bw−1+2,...,M.因此,考虑到所有ki=ki−1= 0情况已对坐席人员1,2,...,bw双休日休班进行指派,情况iii)休班指派之后,已经可保证集E1的M个坐席人员均在双休日至少休班1次.对于生成解中其它坐席人员,步骤5均指派他们在每周双休日休班.因此,生成解能够满足用工制度约束S2.另外,从步骤4至步骤5容易看出,生成解也满足用工制度S3和S4.总结以上分析,有以下结论. 定理3启发式算法H生成问题ILP1的可行排班方案. 由定理2和定理3可知,若算法H结束于步骤4,则生成解是最优排班方案.由于用工制度规定S4可能致使需要更多坐席人力配置,步骤5通过采用类似步骤4 的局部优化策略来补充配置更多坐席人力. 某呼叫中心企业承包若干制造商电子产品售后电话服务业务.企业把坐席人员分为若干服务群组,每个服务群组由十几到几十个坐席人员不等组成,提供由相近产品组成的产品线话务服务支持.坐席人员的当班班种班次设置见表2.假设日内区段时长为1 h,根据区段电话实际呼入量以及承包合同指标TSF要求,使用该群组坐席服务时间统计量,采用Erlang A方法可计算出所有区段坐席人力需求数量rwdt;该参数用来表示排班服务指标TSF要求.计算使用台式计算机的CPU为Intel 酷睿i7四核处理器,主频为2.8GHz.计算实验采用CPLEX 12.1求解整数规划模型;使用C++编程实现启发式算法H. 表2 某呼叫中心的班种班次列表Table 2 List of shift-types and shifts in a call center 下面通过问题实例,说明启发式算法H的计算过程及结果. 1)区段人力需求计算 呼叫中心服务群组工作时间如表2中班次覆盖的15个区段,依次分别用符号t1,t2,...,t15来表示.企业承包制造商服务合同的指标TSF 要求取值85%.根据该群组最近半年(26周)实际数据样本,通过检验拟合分析,确定坐席人员服务率µtd取值0.305/min,顾客耐心时间b取值3.45 min.表3列出该实例每日电话呼入统计量.由表3可看出,周内不同日期电话呼入量差异明显,需要合适指派员工当班/休班日期来满足不同日话务量服务需求.使用Erlang A可计算出4周所有工作区段人力需求.表4列出第2周的周一所有区段电话实际呼入量和人力需求计算结果.由表4可看出,日内不同区段电话呼入量存在波峰波谷现象,需要通过合适安排员工班次来有效应对日内人力需求变化. 表3 问题实例每日电话呼入统计量Table 3 Daily inbound calls of the problem instance 表4 某日内区段呼入量和计算的人力需求分布Table 4 Inbound calls of intervals and calculated labor demands one day 2)员工双休日指派情况 算法H中,步骤1通过模型ILP2计算的(A1,A2,A3,A4)=(6,6,7,7),计算的所有Bwd依次列表为(8,7,7,8,7; 9,9,8,8,8; 8,8,7,8,7; 9,7,9,9,8).由引理1和引理2计算出M=12.步骤2通过对M个坐席人员4个周末当班/休班指派,一方面保证满足每个双休日人力需求,另一方面保证每个坐席人员至少1个双休日休班.由于M个坐席人员尚未覆盖4周所有工作日人力需求,需要通过步骤5 指派坐席人员e13在一些工作日当班.该情况下,坐席人员e13在4个双休日休班.坐席人员双休日当班/休班情况见表5. 表5 坐席人员双休日当班/休班情况Table 5 Attendance of agents on weekends 3)员工工作日指派情况 算法H中,步骤4对坐席人员e1至e12的每周工作日进行休班或当班班次指派.步骤4的班次指派,都是挑选覆盖周内工作日区段人力需求最多的班次,体现了局部贪婪优化思想.步骤5指派坐席人员e13在第4周工作日当班情况为s11{1,3,4,5},其它周工作日均休班.所有坐席人员工作日当班/休班情况见表6.表中符号,如s3,表示坐席人员周内所有工作日班次s3当班;s2{4,5}表示坐席人员在周内周四和周五休班,其它工作日班次s2当班;“—”表示坐席人员周内所有工作日休班. 表6 坐席人员周内工作日当班/休班情况Table 6 Attendance of agents on weekdays 5.2.1 性能评估 从呼叫中心小规模服务群组选择10个问题实例,分别使用ILP1模型和启发式算法H求解排班问题,记录了算法计算时间(s)和计算出的坐席人员数量.这里假设若在1小时内尚未得到最优解,则认为模型ILP1无法获得最优解.具体计算结果见表7. 根据表7,从计算成本与优化性能两方面,对模型和算法分析如下,①模型ILP1 对10个实例的平均计算时间为1 916.5 s,其中2个实例在3 600 s 内未能获得最优解.这表明该排班问题本质上是非常复杂组合优化问题.模型ILP1尽管理论上说可求得问题最优解,但由于其计算成本过大,只适合求解小规模问题.②启发式算法H对10个实例的平均计算时间为35.6 s,远小于模型ILP1的计算成本.这表明该算法具有良好的计算性能.③从优化性能上看,算法H 发现10个实例中的5个最优解,其它实例情况只与最优解(或下界)多1人.这表明算法H无论逐步分解结构,或者班次覆盖区段人力需求特征指标刻画以及局部优化员工指派,能够充分反映该排班问题内在优化规律.算法H能够获得小规模问题实例的最优解或次优解. 表7 小规模问题实例计算结果Table 7 Experimental results of the small-scale problem instances 从较大规模服务群组选择了10个问题实例.由于无法在合理计算时间(1小时内)使用模型ILP1获得问题最优解,通过下界来评估启发式算法H的性能.定义算法H 的性能误差率=(算法H的解评估下界M)/评估下界M.计算结果见表8. 根据表8,对算法H进一步分析如下,①尽管在理论上很难给出步骤1中模型ILP2 求下界M的计算时间复杂度,但如节4中分析所示,步骤2至步骤5的计算时间成本O(rsum)是随着问题规模而线性增长的.对于10个较大规模问题实例,模型ILP1在1小时内无法获得最优解;但算法H的平均计算时间仅为61.4 s.另外,与表7对照可以看出,算法H随着问题规模变大其计算时间增长并不很大.据此可说,算法H能够用来求解大规模排班问题.②从优化性能来看,算法H与评估下界M比较,平均性能误差率不超过5.8%.注意到下界M可能小于最优解(参照表7),表中所示误差率可能低估了算法H的优化性能.据此可说,算法H能够发现大规模排班问题优化解. 表8 较大规模问题实例计算结果Table 8 Experimental results of the large-scale problem instances 5.2.2 问题讨论 排班问题中,用工制度规定S2+S3体现了坐席人员双休日休班公平性; 规定S4 保证坐席人员周内工作日当值相同班次.这些排班规定体现企业人性化管理理念.通过是否保留模型ILP1中描述用工制度规定S2+S3及S4的约束条件式,或者使用算法H(适当修改),可计算讨论这些规定因素对排班人力成本控制的影响.计算结果见表9. 表9 用工制度规定对人力成本影响计算结果Table 9 Experimental results about the influence of labor restrictions on human cost ①从表9可看出,无论考虑保证每个员工至少1个双休日休班,或者保证每个员工每个周内工作日同班次当班,都有可能增加排班用工成本.如果同时考虑两者,用工成本增加可能会更多.表中用工成本最小增长率为0%,意味着针对该实例,借助优化模型算法可实现成本最优,同时兼顾员工双休日休班公平性和保证周内工作日上班规律性. ②保证员工周内工作日上班规律性(S4)比保证员工双休日休班公平性(S2+S3)可能需要更多人力成本.从呼叫中心话务呼入量分布不难看出,一方面,周末呼入量通常比工作日偏少(如见表3),这给员工双休日休班提供了较多机会;只要借助优化模型算法,可较好实现人力成本控制和保证周末休班公平性双重目标.另一方面,周内不同工作日呼入量分布具有不均衡性,同班次规定某种程度上限制了不同工作日人力匹配灵活性,从而引起人力成本上升. ③从表9可看出,呼叫中心业务规模越小,周末休班公平性和同班次用工制度引起的人力成本增加越大.这意味着小规模呼叫中心企业面临着突出的用工成本控制与人性化管理两难问题.当呼叫中心企业规模较大时,人力成本与人性化管理比较容易平衡. 针对呼叫中心企业管理实际需求,研究纳入周末休班公平性和周内工作日同班次约束的多周排班优化问题.通过分析认识问题结构及优化规律,构建问题整数规划模型和提出构造性启发式算法.计算实验表明规划模型适合求解小规模排班问题最优解,而启发式算法能够以小计算成本获得较大规模排班问题优化解.研究结果表明在排班问题中纳入诸如员工诉求及人性化管理因素,尽管对企业长期发展有利,但也可能导致人力成本稍许增加.考虑诸多用工实践情景的坐席人员排班问题,本质上通常是非常复杂的组合优化问题,给学术界提供很多研究机会.3.2 优化性质
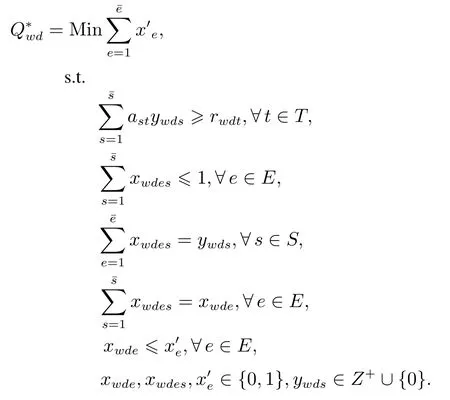
4 启发式算法
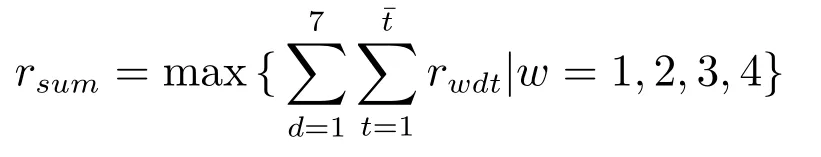
5 计算实验
5.1 实例计算
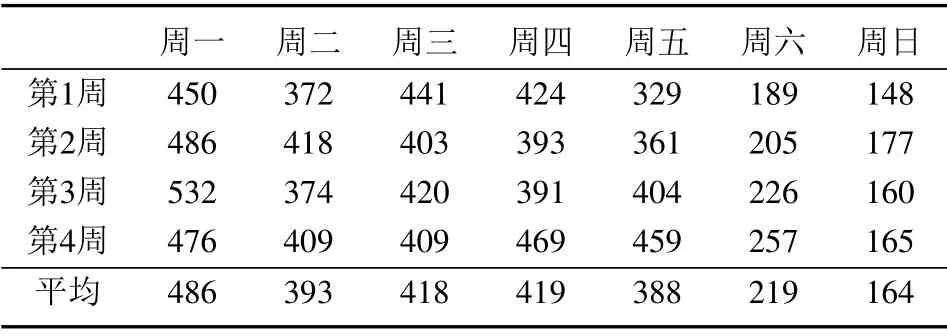
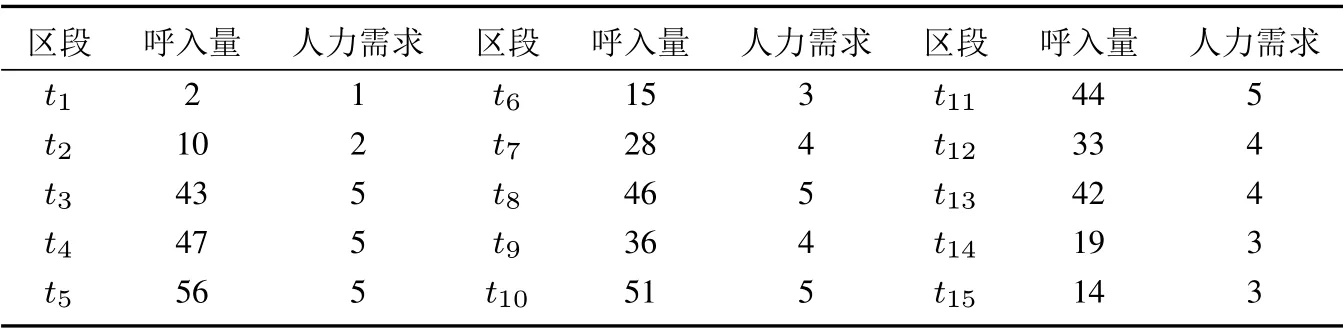
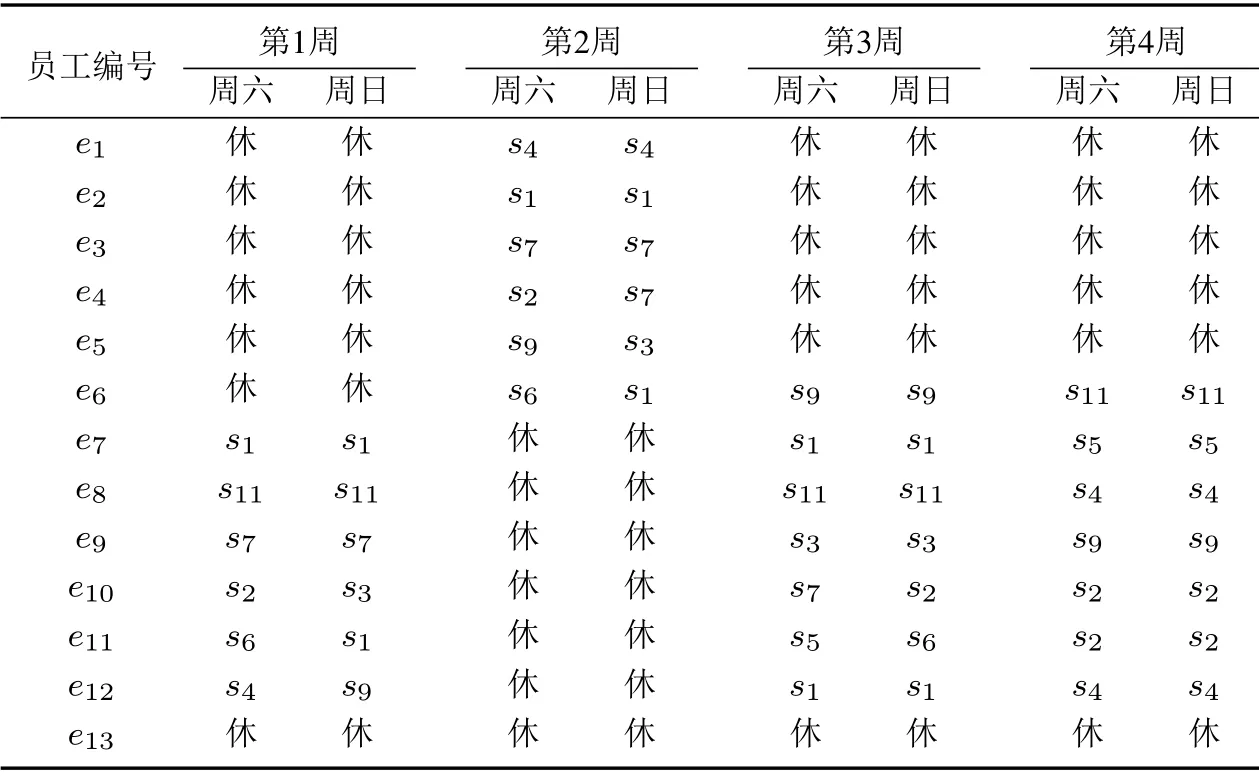
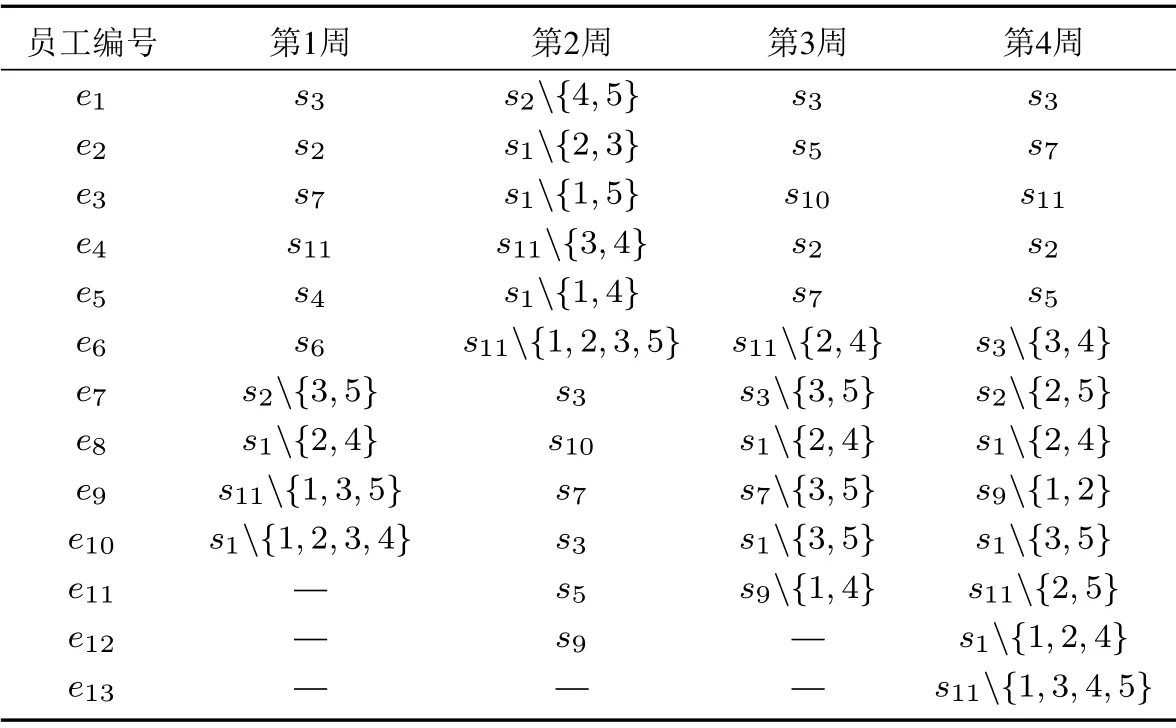
5.2 实验分析
6 结束语

