考虑消费者风险偏好和随机底价的“消费者出价”营销模式
毛照昉,翟孟月
(天津大学管理与经济学部,天津300072)
1 引 言
伴随互联网技术的快速变革和消费者行为的不断成熟,产品、定价、促销和渠道等市场营销策略愈渐成为零售商的决策难题.其中,定价策略因其在市场定位、差异化竞争等方面的重要作用,始终占据重要的战略地位.目前,使用较为普遍的定价策略是单一固定价格模式(posted-price,PP).在该模式下,零售商将产品的定价自主权集中在自己手中,消费者作为价格的接受者,购买意愿和参与程度都相对较低.为改变这一现状,全球著名旅游服务集成商Priceline提出了一种新型的消费者参与式定价模式——消费者出价模式(name-your-own-price,NYOP).在该模式下,零售商不公布产品价格,而是先由消费者根据自身购买意愿自主出价,再由零售商根据成交底价决定是否接受出价并为其提供产品1本文将零售商可接受的消费者出价称为“成交底价”..因此,NYOP模式也常被称为“反(逆)向拍卖定价模式”.与传统拍卖不同,运用NYOP模式时,产品与消费者的对应关系不是一对多,而是多对多,即不同消费者的产品购买结果之间相互独立,不存在个体层面的竞争关系.
自NYOP模式提出以来,国内外学者对其相关问题进行了许多研究.其中,一个重要议题是将其作为不透明营销模式的一种,就其应用场景和适用条件[1−4],以及与其他模式的对比或混合应用[5−9]等进行讨论2常见的“其他模式”有PP模式、最后一分钟促销模式(last minute selling)等..但由于NYOP模式本身具有增强市场细分和扩大消费者需求等优点,也常被作为一种独立的定价模式加以研究.其中,主要的研究方向包括:NYOP模式下消费者的行为特征研究[10−18],零售商的策略选择研究[3,11,19−21],以及模式本身的机制设计[19,20,22−24]等.
在消费者行为特征研究方面,前人主要通过实证或实验方法,对消费者在NYOP模式下的估值(valuation)、摩擦成本(fractional cost)、情绪因素(emotion)以及出价行为(bidding strategy)等进行讨论.这类文献为本文消费者的特征假设提供了理论支持,如消费者估值具有异质性,消费者在出价时普遍具有风险偏好等.但与之不同的是,本文运用数理建模求解方法,着眼于供给侧零售商的策略选择问题,旨在为不同市场环境下的零售商提供最佳策略选择指导.
而在零售商策略选择研究方面,结果呈现出明显的不一致性.一些学者认为,PP模式是零售商的最优定价策略,并对NYOP模式给零售商造成的利润流失进行了原因分析[3,11,19];另一些研究结果则表明,NYOP模式有助于实现价格歧视,零售商选择该模式更具利润优势[20,21].上述文献在研究时大多假设消费者是风险中性的,而Abbas等[18]通过分析NYOP零售商实际的销售数据发现,风险偏好对消费者的出价策略具有很大影响,且消费者在线上渠道的风险厌恶系数相对较高.因此,本文从贴合实际的角度出发,创新性地将消费者的风险偏好特征纳入零售商NYOP模式策略选择研究之中.就目前的研究现状来看,对风险偏好特征的考量包括个体和组织两个层面.个体层面的研究侧重于偏好特征定义和消费者行为影响,多见于渠道选择、促销或拍卖理论等[25−29];而组织层面的研究主要集中在供应链协调问题上[30−33].基于此,本文为排除消费者初始估值对效用比较的影响,借鉴Shapiro[21]对风险厌恶特征的度量方式,对单一垄断和同质化竞争两种情境下零售商的策略选择问题进行了研究.
在出价机制设计方面,以往的研究大致可分为重复出价和底价设置两方面.前者主要是对是否允许消费者重复出价问题的研究,在不同研究背景下的结果并不一致,且在实践中均有应用.一方面,Hann等[10]的研究结果表明,允许重复出价对NYOP零售商来说更有利,因为这种决策在增加总销量的同时能够促进零售商实行价格歧视.另一方面,Fay[20]认为,单次出价策略相对更好,因为这样能缓解竞争.与此同时,Fay[19]通过对“部分‘复杂消费者’偷偷进行重复竞价”背景下,零售商采取单一或重复出价策略的利润对比发现,零售商的策略选择取决于“复杂消费者”的比例.结合Priceline的应用实践,本文在研究过程中假设不允许消费者重复出价,即通过身份信息注册等方式限制消费者的出价次数唯一.在底价设置领域,Fay等[22]研究发现,不论消费者对成交底价的预期积极还是消极,零售商都应公布真实的底价分布信息并采取措施保证其真实性.高明虎等[23]以品牌商品为研究对象,通过建立单、双渠道的NYOP销售模型,对不同渠道模式下产品的最优成交底价进行了研究.鄢章华等[24]在旅游业背景下对上游服务提供商和中间服务集成商之间的底价合作模式进行研究,提出一种具有销量限制的双价格NYOP模式.上述文献从消费者、零售商和供应链协调等多个角度对NYOP模式的底价设置问题进行研究,但大都采用单一固定底价设置方案,即假设零售商采用NYOP模式时的成交底价预先设定且固定不变.显然,当零售商底价固定不变时,部分消费者仍可以通过联合出价和信息共享等方式逐步逼近底价信息,在损害零售商利润的同时,难以满足消费者对价格公平的要求.
综上所述,在不同市场环境下,基于估值异质消费者具有不同风险偏好的假设,研究零售商的策略选择问题,具有一定的理论研究意义,可为零售商的商业实践提供理论指导借鉴.为此,本文引入随机底价和概率成交的思想,提出一种名为Random-NYOP(简称“RN模式”)的新型NYOP定价模式.在该定价模式下,零售商的成交底价从某确定区间中随机选择,消费者出价越高成交概率越大,同时存在拒绝高出价消费者而接受低出价消费者的可能.虽在直观上,拒绝高出价消费者不够明智,但这样可以通过成交底价的不可知性有效保证消费者的出价成交公平性.同时,随机底价RN模式的提出,能够规避消费者在传统NYOP模式下的投机行为,在确保成交底价不可知性的条件下,维护底价的公平性和真实性.基于此,本文旨在运用数理建模方法,对以下三个问题进行研究:首先,对于单一垄断零售商而言,消费者的风险厌恶特征如何影响其出价行为;其次,消费者出价行为的改变如何影响零售商的策略选择;最后,竞争环境下两家同质化零售商应如何选择合适的定价策略.
为解决上述问题,本文在消费者估值异质且具有不同风险偏好等的假设条件下,通过建模分别对单一零售商垄断和两家同质化零售商竞争情形展开分析.首先,以消费者效用最大化为目标,求解最优出价策略,并对不同风险偏好消费者的出价行为作对比分析;然后,通过对比零售商采用RN或PP模式时的最大期望利润,分析消费者行为对其利润的影响;最后,在竞争环境下对比“同时采用PP模式”、“同时采用RN模式”和“一方采用PP,一方采用RN”等三种策略组合,求解各种策略下两家零售商的最优均衡.研究表明,单一垄断情形下,具有风险厌恶特征的消费者为降低因价格信息不可知造成的出价失败风险,会比风险中性消费者出价更高,使得零售商在该情形下更愿意采用RN定价模式;同质化竞争情形下,“一方PP,另一方RN”的差异化定价策略能够有效缓解两家零售商之间的正面价格竞争,使其达到纳什均衡.
2 模型描述及相关符号说明
本文研究分为单一垄断和同质化竞争两种市场情形,对零售商定价及策略选择问题进行研究.首先,在单一垄断情形下,假设市场上有一家零售商采用批发合同形式从某单个制造商处购进某产品并销售给消费者3当市场上存在一家实力明显超越其他零售商的领导者时,也属于该单一垄断情形讨论的范围.;接着,在同质化竞争情形下,假设市场上有两家零售商从单个制造商处以相同的批发价格购进某产品并面向同一消费市场销售.同时,在这两种情形下分别考虑消费者的风险偏好类型为中性(risk-neutral,RN)或厌恶(risk-aversion,RA)的情况.上述供应链系统分别如图1(a)和图1(b)所示.
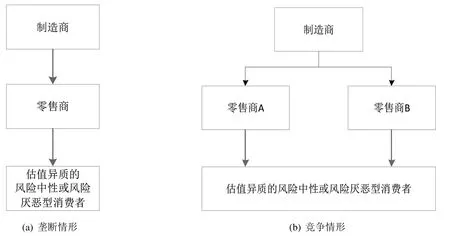
图1 两种不同情形下的供应链系统模型Fig.1 Supply chain system model under the two different conditions
为方便下文的模型分析,作出如下六条假设:
假设1包括零售商和消费者在内的所有参与者都是策略型的,以自身利润或效用最大为目标进行策略选择.对零售商来说,它的策略集合包括“PP模式”和“RN 模式”两个元素;对消费者来说,具有“出价购买”和“离开市场”两种选择.不同定价模式对消费者决策的影响主要体现在“是否具有出价自主权”.PP模式下,消费者属于“价格接受者”;而在RN模式下,消费者属于“定价者”.
假设2决策的顺序是,先由零售商选择定价模式,再由消费者选择是否购买.若零售商采用RN模式,消费者在决策是否购买的同时,还要根据自身情况决定出价多少.
假设3消费者价格敏感且估值异质.不失一般性地,假设消费者的估值v服从[0,1]的均匀分布.
假设4消费者因价格信息公开程度不同而对购买风险持中性或厌恶两种偏好.对风险中性消费者而言,不论产品的价格信息是否公开,其效用函数表达式均为urn=u(v); 而对风险厌恶消费者而言,当价格信息不公开时,其效用函数表达式为ura= [u(v)]α,其中,α为“风险厌恶系数”,α越大,消费者的风险厌恶程度越小.衡量消费者风险厌恶程度的同时,能够有效排除消费者初始估值对其效用比较的影响[21]且0<α<1.
假设5零售商采用RN模式时,成交底价在区间[l,h]上随机选择且h>l4当h=l时,RN模式与PP模式等价,故假设分布上界h严格大于下界l,即h>l..不失一般性地,假设成交底价服从[l,h]的均匀分布,概率密度函数为g(·).为简化计算,在不影响直观性结论的前提下,假设竞争环境下成交底价的分布区间为[0,1],且竞争双方信息对称.
假设6消费者在RN模式下的出价用b表示,且出价机会唯一.则风险中性消费者在该模式下的效用表达式为urn=v −b;风险厌恶消费者在该模式下的效用表达式为ura=(v −b)α.
为突出研究问题,在上述假设的基础上,不失一般性地认为,消费者具有单位需求且市场容量为1;零售商从单个制造商处购进产品的批发价格为零且无订货提前期.
垄断情形下的参数上标rn和ra分别表示消费者的风险偏好为中性或厌恶,下标PP和RN分别表示零售商采用单一固定价格模式或随机底价的消费者出价模式.竞争情形下的上标(PP,PP),(PP,RN)和(RN,RN)分别表示两家零售商的不同模式组合,即“同时采用PP”,“一方采用PP,一方采用RN”,以及“同时采用RN”;下标A和B分别表示两家零售商.上标“*”表示最优性.
模型使用的主要符号及其含义如表1所示.

表1 主要符号及含义说明Table 1 Main symbols and implications
本文分别对单一垄断和同质化竞争两种情形下,零售商的销售策略选择问题进行研究.首先,通过对比零售商采用PP或RN模式时的期望利润,确定RN模式的适用情境并分析其运作原理;然后,通过对比两家同质化零售商采用不同策略组合时的期望利润,确定双方竞争的纳什均衡策略,分析竞争情形下RN模式的适用性及实施方案.
3 单一垄断零售商的最优模式选择
3.1 采用PP模式
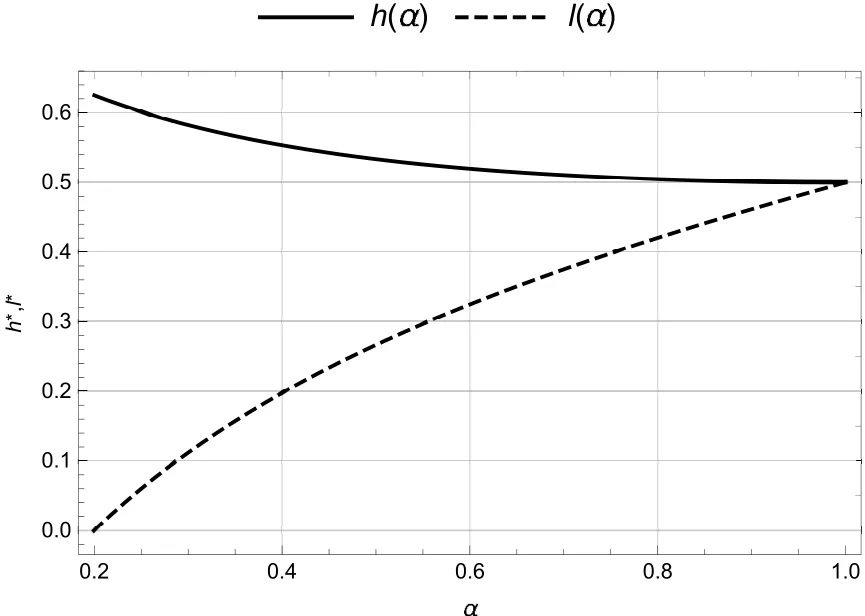
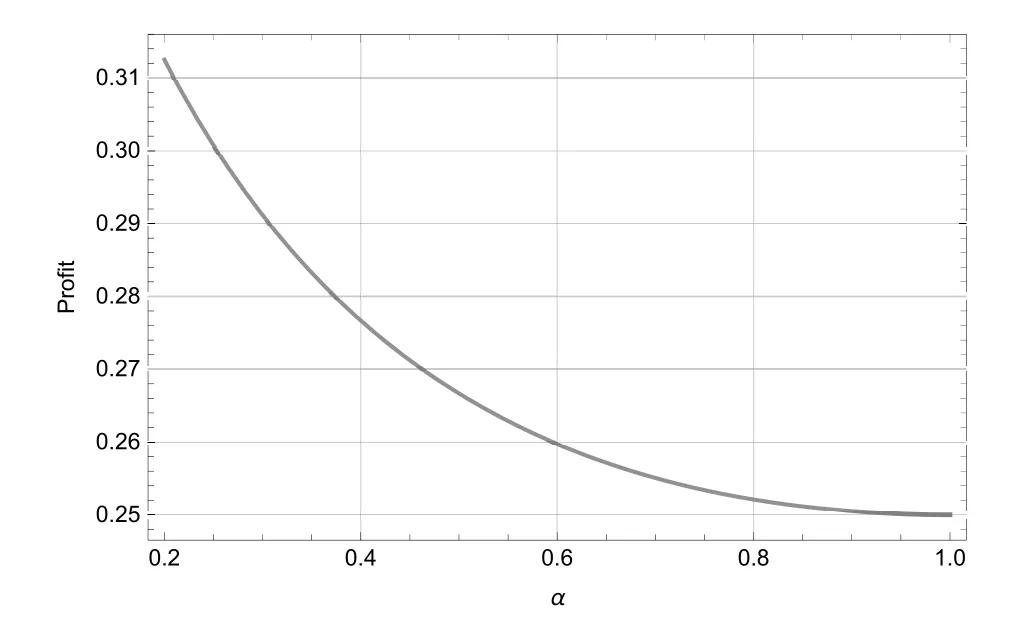
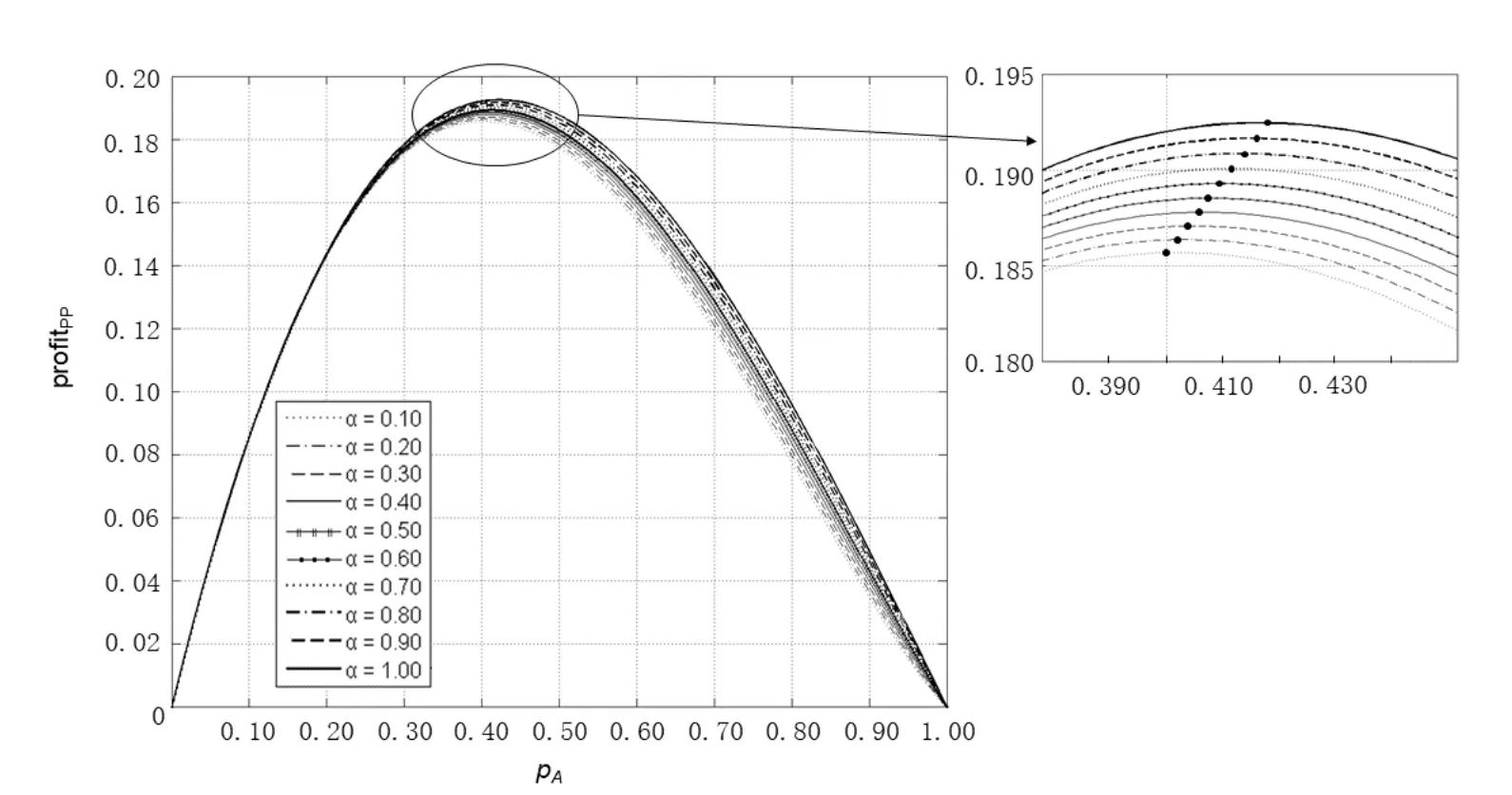
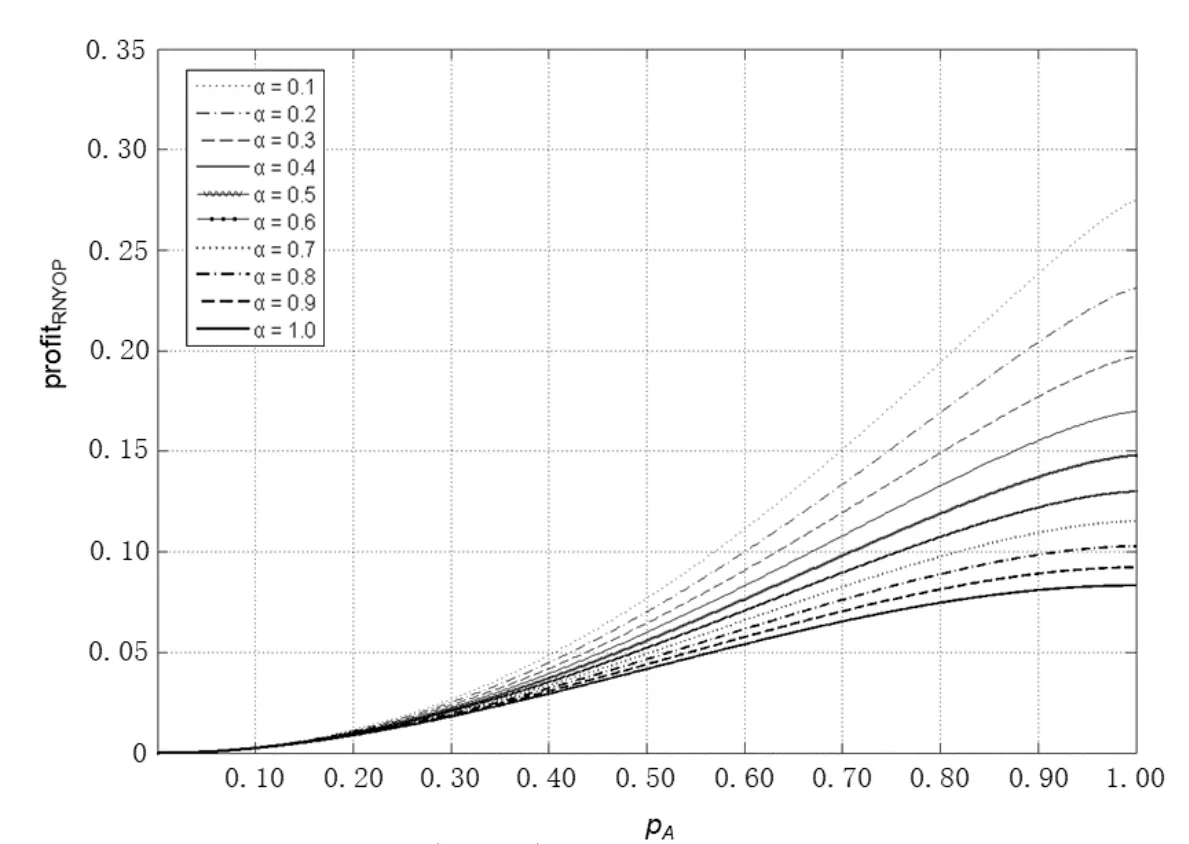
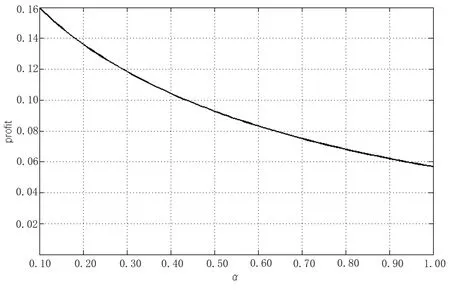
当单一垄断零售商采用PP模式时,消费者能够准确获知产品的销售价格pPP,不存在因价格信息不确定引发的购买失败风险.此时,风险中性和风险厌恶消费者的期望效用函数形式相同,均为E[u]=v −pPP.基于此,市场上消费者因其估值差异可分为以下两种类型:v >pPP的“高估值”消费者和v 因此,单一垄断零售商采用PP模式时的期望利润函数为 显然,ΠPP是定价策略pPP的二次凹函数,存在极大值.基于此,易得单一垄断零售商采用PP模式时的最优定价策略及其对应的最大期望利润,如命题1所述. 命题1若单一垄断零售商采用PP模式,则其最优定价策略为可获得的最大期望利润为 由命题1可以看出,在PP模式下,消费者按照PP模式的最优定价(即市场上所有消费者估值的平均水平)决策是否购买,不存在风险偏好的影响.即市场上所有消费者估值的平均水平.此时,市场上一半的消费者无法通过购买产品获得正效用,直接离开;一半的消费者选择以固定价格购买,且效用随其自身估值的增大而增大.因此,零售商采用PP模式时的边际利润固定不变,始终为;盈利规模是估值大于的那部分消费者,使得其最终可获得的期望利润为 当单一垄断零售商采用RN模式时,产品的成交底价可在区间内随机选择,具有不确定性.消费者因其风险偏好类型的差异,具有不同的效用函数.下面根据消费者风险偏好类型为中性和厌恶两种情形分别展开讨论. 3.2.1 消费者风险偏好为中性的情形 首先讨论消费者的出价策略.单一垄断零售商采用RN模式时,风险中性消费者通过购买产品可获得的期望效用为 将该极大值点与边界值l和h比较可得,当0v < l时,brn∗= 0; 当lv <2h −l时,为最大值点; 当2h −lv1时,brn∗=h.也就是说,单一垄断零售商采用RN模式时,风险中性消费者因其估值异质性,自发地分为以下三种类型:v ∈[0,l)的“低估值”消费者,其最优决策是不购买产品,直接离开市场,可获得的期望效用为零;v ∈[l,min{2h −l,1})的“中估值”消费者,其最优出价策略是成交底价区间下界l及其自身估值的增函数,估值越高的消费者出价越高,可获得的期望效用为v ∈[min{2h −l,1},1]的“高估值”消费者,其最优出价策略为成交底价区间上界h,可获得的期望效用为(v −h)α. 综上,单一垄断零售商采用RN模式时,风险中性消费者的最优出价策略为 下面讨论零售商利润,由式(2)可知,单一垄断零售商在面向风险中性消费者采用RN模式时,可得的期望利润为 化简式(3)可得 图2 零售商采用RN模式时的定价可行域Fig.2 The feasible region of pricing when retailers use RN mode 命题2若市场上估值异质消费者的风险偏好类型均为中性,则单一垄断零售商采用PP模式更佳,且最优定价策略及可获得的期望利润如命题1所述. 由计算过程可知,当消费者的风险偏好类型为中性时,单一垄断零售商采用RN模式可以吸引更多的消费者参与出价,扩大市场需求,称其为“增需正效应”;但同时使得许多原本在PP模式下以价格购买产品的消费者在RN模式下购得产品的价格降低,减少了零售商从单个消费者处获得的边际利润,称其为“流失负效应”.从零售商最终的利润情况来看,在风险中性消费者市场上采用RN模式的负效应更大,使得PP模式表现相对更优. 3.2.2 消费者风险偏好为厌恶的情形 与3.2.1节类似,首先讨论消费者的出价策略.单一垄断零售商采用RN模式时,风险厌恶消费者通过购买产品可获得的期望效用为 类似地,通过该极值点与边界值的比较,可以得到该情形下的消费者划分:v ∈[0,l)的“低估值”消费者,其最优决策是不购买产品,直接离开市场,可获得的期望效用为零;v ∈[l,min{(1+α)h −αl,1})的“中估值”消费者,其最优出价策略除了与l和v有关,还会受到风险厌恶参数α的影响,其最优出价策略为bra∗=可获得的期望效用为v ∈[min{(1+α)h −αl,1},1]的“高估值”消费者,其最优出价策略为成交底价区间上界h,可获得的期望效用为(v −h)α. 综上,单一垄断零售商采用RN模式时,风险厌恶消费者的最优出价策略为 通过式(2)和式(5)的比较可以看出,风险偏好类型不会影响“低估值”或“高估值”消费者群体的最优出价策略,但会给市场细分造成以下两方面影响:首先,v ∈[l,min{(1+α)h −αl,1})的“中估值”消费者出价相对更高;其次,v ∈[min{(1+α)h −αl,1},1]的“高估值”消费者数量增多.这是因为,风险厌恶消费者想通过出高价来提高自己获得产品的概率,从而抵御因产品销售价格不确定造成的出价失败风险.此外,命题3讨论了“中估值”消费者最优出价策略关于风险厌恶参数α的敏感性分析. 命题3若单一垄断零售商采用RN模式,则对估值v ∈[l,min{(1+α)h −αl,1})的风险厌恶消费者而言,其最优出价策略bra∗是其风险厌恶系数α的减函数. 由命题3可知,对于“中估值”消费者而言,其自身的风险厌恶系数α越小(即风险厌恶程度越强),对应的最优出价策略越大.换言之,随着α减小(即风险厌恶程度增强),消费者对风险的容忍程度越低,越愿意出高价来增大产品的购买成功概率.在设定l= 0,的基础上,分别取α= 0.2,0.4,0.6和0.8绘制如图3所示的数值分析图. 从图3中可以看出,对于某一估值确定的消费者而言(如v= 0.4),随着消费者风险厌恶系数α的减小(即风险厌恶程度增强),消费者的最优出价bra∗不断提高,验证了命题3中结论. 下面讨论零售商利润.由式(5)可知,单一垄断零售商在面向风险厌恶消费者采用RN模式时,可获得的期望利润为 化简式(6)可得 图3 消费者最优出价bra∗随风险厌恶系数α的变化Fig.3 Changes of bra∗with the degree of risk aversion coefficient α 命题4当市场上消费者的风险厌恶程度非常高,即时,单一垄断零售商的最优利润点无法取到,可转而采用次优策略,即底价分布区间为此时对应的期望利润为;当消费者的风险厌恶程度相对减弱,即时,成交底价的最优分布区间为零售商可获得的最大期望利润为 由命题4可进一步得到如下两条推论,并作相应数值分析如图4和图5所示. 图4 h∗和l∗随风险厌恶系数α的变化Fig.4 Changes of h∗and l∗with the degree of risk aversion coefficient α 图5 (l,h)随风险厌恶系数α的变化Fig.5 Changes of (l,h)with the degree of risk aversion coefficient α 推论1当时,单一垄断零售商采用RN模式时的最优底价分布区间上界h随消费者风险厌恶系数α的增大而减小,下界l随α的增大而增大.特别地,当α增大到1时消费者不具有风险厌恶特征,相当于风险中性的情形,此时 推论2当时,单一垄断零售商采用RN模式可获得的最大期望利润随消费者风险厌恶系数α的增大而减小.且当时,当α= 1时,0.25. 通过上述分析容易推断,l,h和(l,h)等关键变量随风险厌恶系数α产生上述变化的原因,主要源自系数α对消费者出价策略的影响.具体而言,随着α的增大,消费者的风险厌恶程度不断下降,对消费者出价的正向激励作用逐渐减小,为零售商带来的边际利润优势随之减小.因此,降低h可以减少因消费者流失带来的利润负效应,增大l可以增大零售商边际利润从而增大正效用.换句话说,随着系数α的增大,降低h增大l是零售商利润最大化目标的体现和必然要求.但需要注意的是,随着α的增大,利润的正向激励作用不断下降,负效用不断增强,导致零售商的最终利润逐渐减小. 最后讨论单一垄断零售商在该情形下的策略选择问题.通过与3.1节命题1中结论的对比分析,可以得到零售商在面对风险厌恶消费者时的策略选择,结论如下. 命题5若市场上估值异质消费者的风险偏好类型均为厌恶,则不论其风险厌恶程度如何,单一垄断零售商采用RN模式的盈利能力更强,且最优策略如命题4所述. 通过与命题2的对比可以看出,消费者的风险偏好对单一垄断零售商的策略选择具有重要影响.具体而言,当消费者的风险偏好类型为中性时,零售商选择PP模式更优;当消费者的风险偏好类型为厌恶时,零售商选择RN模式更优.这是因为,风险厌恶的消费者为抵御因价格信息不可知造成的购买失败风险,会相对风险中性的消费者出价更高.这种行为会给零售商的利润造成以下两方面的正向影响:首先,增大零售商从单一消费者身上获得的边际利润;其次,出高价的“高估值”消费者群体增大.从零售商可获得的期望利润来看,这种正向影响远大于命题2分析部分提到的利润流失负效应,使得RN模式在该情形下对零售商而言更具优势. 通过本节分析可以看出,若市场上估值异质的消费者是风险中性的,则单一垄断零售商的最优策略是PP模式,该模式下消费者需求量虽不及RN模式,却可以获得更大的边际利润.若消费者是风险厌恶的,则单一垄断零售商可以根据消费者的风险厌恶系数α的不同,制定相应的最优成交底价分布区间策略[l∗,h∗],从而获得比PP模式更多的利润.与此同时,单一垄断零售商采用RN模式可获得的相对利润优势,随消费者风险厌恶程度的下降而减小. 当两家零售商均选择PP策略时,消费者能够准确获知产品的销售价格pPP,不存在因价格信息不确定引发的购买失败风险.此时,消费者的期望效用函数为E[urn]=v −pPP.根据伯特兰德模型(Betrand Duopoly Model)结论可知,两家零售商的均衡价格策略相同且等于各自的边际成本,即pA=pB=w=0.此时,两家零售商进行激烈的价格竞争,谁也无法从中获利,最终可获得的期望利润为 当两家零售商分别采用PP和RN两种不同的定价模式时,根据对称性,可以不失一般性地假设零售商A采用PP模式,而零售商B采用RN模式.分别考虑消费者风险偏好为中性和厌恶的情形. 4.2.1 消费者风险偏好为中性的情形 对于采用PP模式的零售商A而言,只有将价格pA设定在[0,1]之间才能获得大于零的利润,即pA1;否则,需求量为零.因此,可以将市场上的消费者分为两类:0v < pA的“低估值”消费者和pAv1的“高估值”消费者. 首先讨论消费者的出价策略.对“低估值”消费者来说,只有在“零售商B处出价”或“直接离开市场”两种选择;但对于“高估值”消费者来说,具有“先在零售商B处出价,若失败则转回零售商A”、“直接以价格pA在零售商A处购买”以及“直接离开市场”三种选择,如图6所示. 图6 消费者出价策略示意图Fig.6 The selections of consumers’bidding strategies 对于“低估值”消费者而言,选择在“零售商B处出价”可获得的期望效用为 选择“直接离开市场”可获得的期望效用为零.因此,“低估值”消费者最优出价策略为 对于“高估值”消费者而言,选择“先在零售商B处出价,若失败则转回零售商A”可获得的期望效用为显然,E[u1]是消费者出价b的二次凹函数,存在极大值.令可得,对应的消费者期望效用为E∗[u1]=选择“直接在零售商A处以价格pA购买”可获得的期望效用为E[u2]=v −pA.选择“直接离开市场”可获得的期望效用为零.显然,E∗[u1]>E[u2]>0.因此,“高估值”消费者的最优出价策略为“先在B处以出价,若失败则转到A处以价格pA购买”. 因此,消费者在该情形下的最优出价策略为 由式(10)可知,零售商A和零售商B在该情形下可获得的期望利润分别为 分别化简式(11)和式(12)可得 通过式(13)和式(14)的计算容易得到,竞争环境下零售商A的最优定价策略p∗A及两家零售商分别对应的期望利润,如命题6所述. 命题6在消费者风险偏好为中性的情形下,从单一制造商处进货的两家零售商进行同质化竞争时,若双方分别采用PP和RN定价模式,采用PP模式的零售商的最优定价策略为可获得的最大期望利润为采用RN模式的零售商可获得的期望利润为 由命题6可以看出,在两家同质化零售商竞争的环境下,采用差异化的定价模式相对于双方均采用PP模式更具利润优势.具体而言,当选择RN 模式的零售商对外公布的成交底价pRN的分布区间为[0,1]上的均匀分布时,采用PP模式的零售商的最优定价策略为使得PP零售商获得的利润,RN零售商获得的利润.相较于竞争双方同时采PP模式的情形,零售商利润分别增长了约19.25%和3.21%. 4.2.2 消费者风险偏好为厌恶的情形 选择“直接离开市场”可获得的期望效用为零.“低估值”消费者的最优出价策略为 对于“高估值”消费者而言,选择“先在零售商B处出价,若失败则转回零售商A”可获得的期望效用为选择“直接在零售商A处以价格pA购买”可获得的期望效用为E[u4]=(v −pA)α.选择“直接离开市场”可获得的期望效用为零.可证E[u3]>E[u4],因此,“高估值”消费者的最优出价策略为“先在B处以b出价,若失败则转到A处以价格pA购买”. 为求得使“高估值”消费者“先在B处以b出价,若失败则转到A处以价格pA购买”效用最大的出价,令在此先设该方程的解为bo,即arg max E[u3]=bo.根据假设5,竞争环境下采用RN模式的零售商成交底价的分布区间为[0,1],因此,消费者在风险厌恶情形下的最优出价策略为 由式(17)可知,零售商A和零售商B在该情形下可获得的期望利润分别为 分别化简式(18)和式(19)可得 图7和图8分别显示了消费者不同风险偏好下零售商A和零售商B定价策略与利润的变化趋势. 图7 随PP零售商定价pA的变化Fig.7 Changes of with the pricing of the PP retailer pA 假设市场上存在1 000个估值异质且具有风险厌恶特征的消费者.零售商A 可以从某一高估值消费者处获得pA(1−bo)的利润,而零售商B从某一高估值消费者处获得bo2的利润,或从某一低估值消费者处获得的利润,则两家零售商各自的总利润即为所有在其处成功购买商品的消费者利润的累加. 图中显示,消费者风险厌恶程度一定时,随定价pA增加,PP零售商的利润从0增加至最大值,而后又逐渐减小至0; 当定价pA一定时,消费者风险厌恶程度越小(即α越大),PP零售商的利润越大.具体来说,当α从0.1增至1.0时,PP零售商的最优定价p∗A从0.400增至0.425,其最大利润相应从0.185 7增至0.192 5.对于RNYOP零售商而言,PP零售商定价pA增加使其利润单调递增,且消费者风险厌恶程度越大(即α越小)RNYOP零售商的利润越大.当PP零售商定价pA为0时,所有消费者都将放弃在RNYOP零售商处出价,而选择直接在PP零售商处免费获得商品,由此PP零售商和RNYOP零售商都无法从中获利,即ΠA(PP,RN)和ΠB(PP,RN)都为0.两家零售商的利润随风险厌恶系数α产生上述变化的原因,主要源自系数α对消费者出价策略的影响.具体而言,根据效用最大化理论,所有消费者都会选择先在RNYOP零售商处出价,而非直接在PP零售商处直接以pA购买.在此基础上,随着α减小,消费者的风险厌恶程度不断增加,更愿意在RNYOP零售商处出高价来避免购买失败的风险,为RNYOP零售商带来的边际利润优势增加,同时,更高的出价保证了消费者在RNYOP零售商处更大的成功购买概率,使因在RNYOP零售商处购买失败而转回PP零售商购买的人群减小.也就是说,随着α减小,RNYOP零售商利润的正向激励作用不断增加,而在PP零售商处购买的消费者不断减少,最终导致PP零售商利润下降而RNYOP零售商利润上升. 图8 随PP零售商定价pA的变化Fig.8 Changes of with the pricing of the PP retailer pA 4.3.1 消费者风险偏好为中性的情形 首先讨论消费者的出价策略.当两家零售商均选择RN模式时,消费者具有五种策略选择:(1)先在A出价,若失败则转到B处出价;(2)先在B出价,若失败则转到A处出价;(3)先在A出价,若失败则离开市场;(4)先在B出价,若失败则离开市场;(5)直接离开市场. 由于模型假设的对称性,只需比较消费者在选择(1)、(3)和(5)下的期望效用. 当消费者选择策略(1)时,可获得的期望效用为 其中b1表示在先选择的零售商处的出价,b2表示在后选择的零售商处的出价.显然,E[u(1)]是b1和b2的凹函数,存在极大值组合(b1,b2)使得效用最大.故令可以得到b1=及此时,消费者可获得的最大期望效用为当消费者选择策略(3)时,最优出价策略和对应的最大期望效用与3.2节相同,即当消费者选择策略(5)时,可获得的期望效用为E[u(5)]=0. 容易证得,E[u(1)]>E[u(3)]>E[u(5)].因此,在该情形下,所有消费者均会选择先后在两家零售商处出价,且先出价后出价 下面讨论两家零售商在该情形下的利润情况.由于两家零售商具有对称性,可以不失一般性地假设,消费者先选择某家零售商的概率相同.则此时两家零售商可获得的期望利润相同,均为 通过与3.1节中两家零售商同时采用PP模式可获得的最大期望利润进行比较,可以得到,两家零售商均采用RN模式时可获得的期望利润相等,且大于同时采用PP模式时的均衡利润,增大的比例约为5.68%.这是因为,价格的不透明性减弱了两家零售商之间的直接价格竞争,间接提升了零售商的边际利润. 4.3.2 消费者风险偏好为厌恶的情形 与4.3.1节分析类似,所有消费者都会选择先后在两家零售商处出价.不失一般性地,假设消费者先在A处出价b1,若失败则转到B处出价b2,则消费者的期望效用为 为求解使消费者效用最大的最优出价策略b∗1和b∗2,令b2(v −b2)α= 0且= (1−b1)(v −(1+α)b2)(v −b2)α−1= 0.由可得,或b∗2=v.显然消费者出价会尽可能低于估值,故合理,将b∗2代入中得到关于b1的隐函数方程(v −(1+α)b1)(v −b1)α−1=由于两家零售商具有对称性,可以不失一般性地假设,消费者先选择某家零售商的概率相同.则此时两家零售商可获得的期望利润相同,均为 图9直观地展示了市场上存在1 000个具有风险厌恶特征且估值异质的消费者时,两家零售商利润随消费者风险厌恶程度的变化趋势.当α ∈(0,1]时,随α增大,即消费者风险厌恶程度减小,零售商的利润下降;反之,随α减小,消费者风险厌恶程度增加,零售商的利润上升.原因如前所述,当消费者风险厌恶程度增加时,愿意出更高的价格以避免因出价过低而造成的购买失败风险,而此时所有成功购买商品的消费者的出价构成零售商的总利润. 图9 (l,h)随风险厌恶系数α的变化Fig.9 Changes of (l,h)with the degree of risk aversion coefficient α 根据4.1节∼4.3节中两家零售商不同模式组合情况下期望利润的计算,可以得到消费者风险偏好为中性情形下该博弈问题的支付矩阵,如表2. 表2 消费者为风险中性时不同模式组合下两家零售商的支付矩阵Table 2 Payoff matrix of two retailers under different modes when consumers are risk-neutral 根据纳什均衡的求解方法可得,若零售商A先进行模式选择,则当其选择PP模式时,ΠB(PP,RNYOP)=零售商B会选择RNYOP模式; 当其选择RNYOP模式时,零售商B会选择PP模式.同理,若零售商B先进行模式选择,则当其选择PP模式时,零售商A选择RNYOP模式更优;当其选择RNYOP模式时,零售商A选择PP模式更优.也就是说,策略(PP,RNYOP)和(RNYOP,PP)是该环境下的纯策略纳什均衡解.该结果概括在命题7中. 命题7两家同质化零售商竞争时的最优策略组合是(PP,RNYOP)或(RNYOP,PP),零售商的定价策略及分别对应的最大期望利润如命题6所述. 在上述讨论的基础上,考虑消费者为风险厌恶时两家零售商的模式选择问题. 根据纳什均衡的求解方法可得,消费者为风险厌恶时,若零售商A先进行模式选择,则当其选择PP模式时,ΠB(PP,RN)=[0.002 6,0.005 2]>0 =ΠB(PP,PP),零售商B会选择RN模式; 当其选择RN模式时,ΠB(RN,PP)= [0.185 7,0.192 5]> ΠB(RN,RN)=[0.056,0.160],零售商B会选择PP模式.同理,若零售商B先进行模式选择,结论与上述相同. 表3 消费者为风险厌恶时不同模式组合下两家零售商的支付矩阵Table 3 Payoff matrix of two retailers under different modes when consumers are risk-aversion 综上所述,不论市场上估值异质消费者的风险偏好类型为中性还是厌恶,两家零售商的最优策略组合都是分别采用不同的定价模式,即双方差异化定价模式.具体而言,在两家同质化零售商竞争的情形下,消费者的风险偏好类型为中性时,先进行模式选择的零售商(A或B)会选择PP模式且定价为从而获得的期望利润; 后选择的零售商(B或A)采用RN模式,可获得的期望利润为消费者的风险偏好类型为厌恶时,在市场上存在1 000个估值异质消费者的情形下,受消费者风险厌恶系数α的影响,PP零售商的最优定价在[0.400,0.425]之间变化,从而先进行模式选择的零售商(A或B)会选择PP模式获得[0.185 7,0.192 5]的期望利润; 后选择的零售商(B或A)采用RN模式,可获得的期望利润为[0.002 6,0.005 2]. 本文基于随机底价和概率成交思想,提出了一种新型RN定价模式.该模式在扩大市场需求和实现价格歧视的同时,能够保障消费者之间的价格相对公平.本文在消费者估值异质的假设下,对单一垄断和同质化竞争两种情形下零售商的策略选择问题进行了研究.结果表明,单一垄断情形下,消费者的风险偏好会影响其出价行为,并进一步对零售商的策略选择造成影响.具体而言,若估值异质消费者的风险偏好为中性,零售商采用PP模式更佳;若消费者的风险偏好为厌恶,零售商采用RN模式可获得的期望利润更大,且相对利润优势随着消费者风险厌恶程度的增强而增大.与此同时,在同质化竞争情形下,无论消费者是否具有风险厌恶性质,都会有零售商愿意采用RN模式;且“一方采用PP模式,另一方采用RN模式”始终是使双方达到纳什均衡的最优策略组合.原因在于RN模式成交底价的随机性弱化了同质化零售商双方的正面价格竞争,从而扩大了双方的利润. 本文当前研究的局限性主要体现在消费者估值异质和风险厌恶程度的假设上.首先,消费者估值服从[0,1]的均匀分布虽是本领域的常用假设,但与现实情境之间仍有一定差异;其次,本文假设市场上所有消费者在风险厌恶程度方面具有同质性,即风险偏好系数α相同.在今后研究中,可从以下两个方面进行改进:第一,采用实证分析或实验模拟等方法对消费者的估值分布做出更符合现实情境的假设;第二,针对消费者风险厌恶程度异质性情形做进一步的深入研究.
3.2 采用RN模式

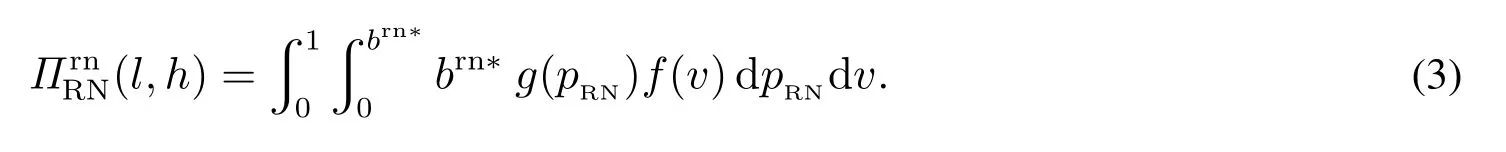

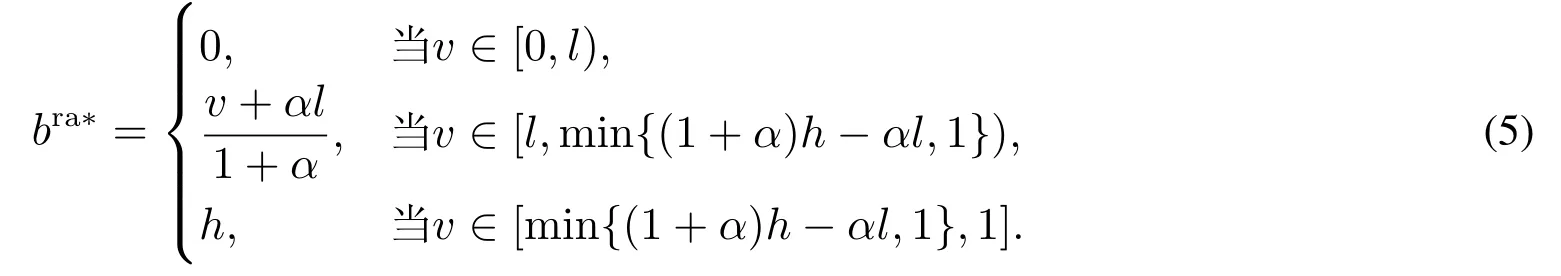
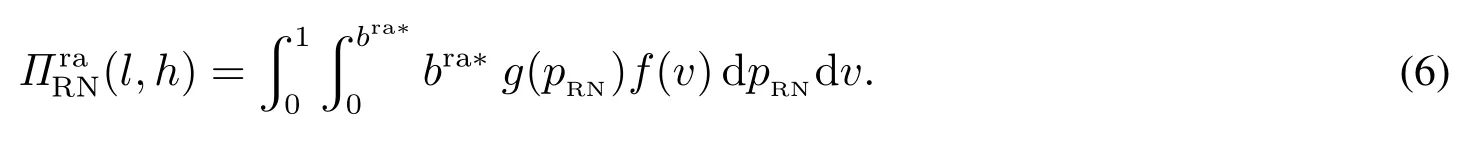


4 两家同质化零售商的最优模式选择
4.1 两家零售商均采用PP模式的情形
4.2 一家采用PP模式,一家采用RN模式的情形

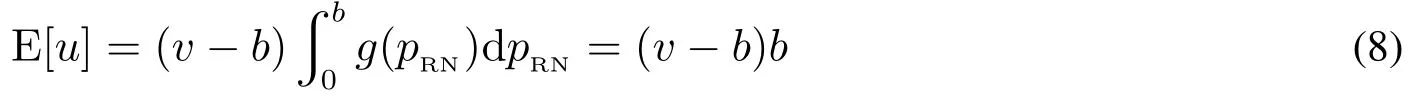


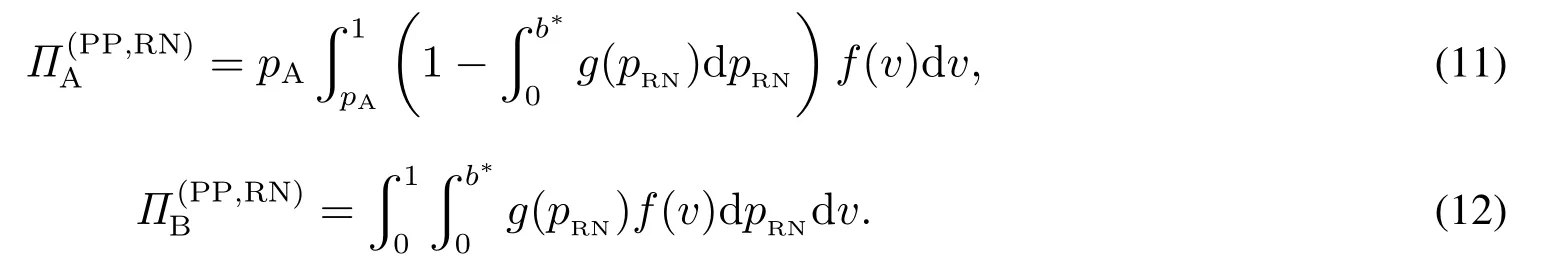
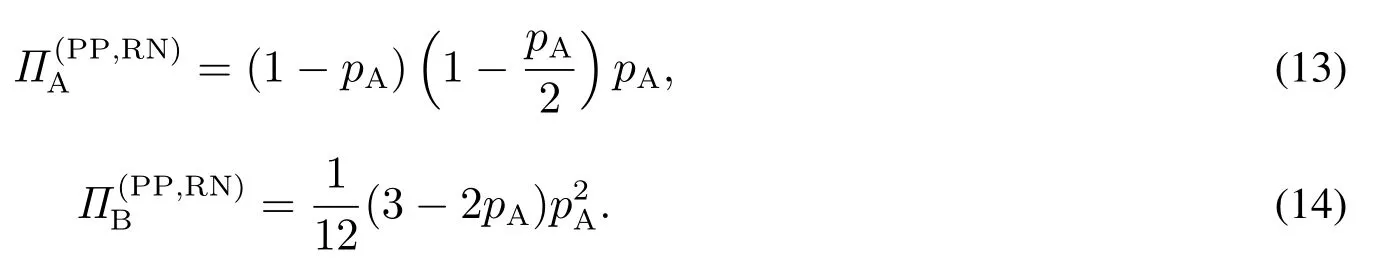

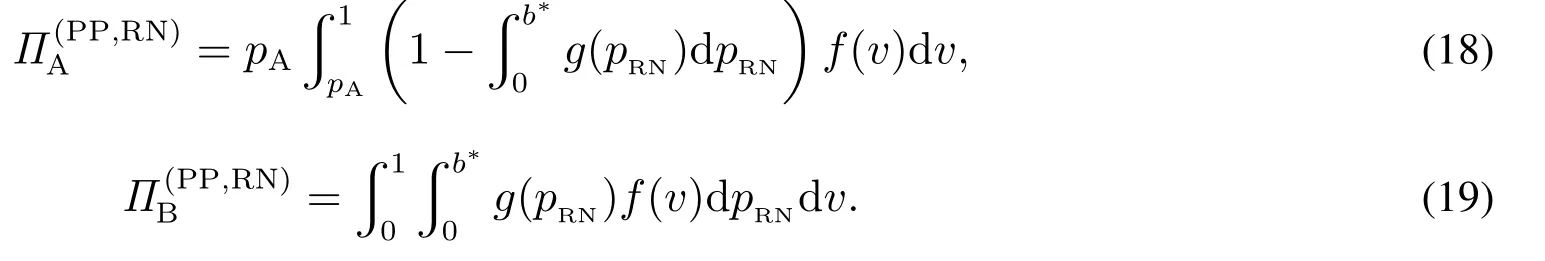
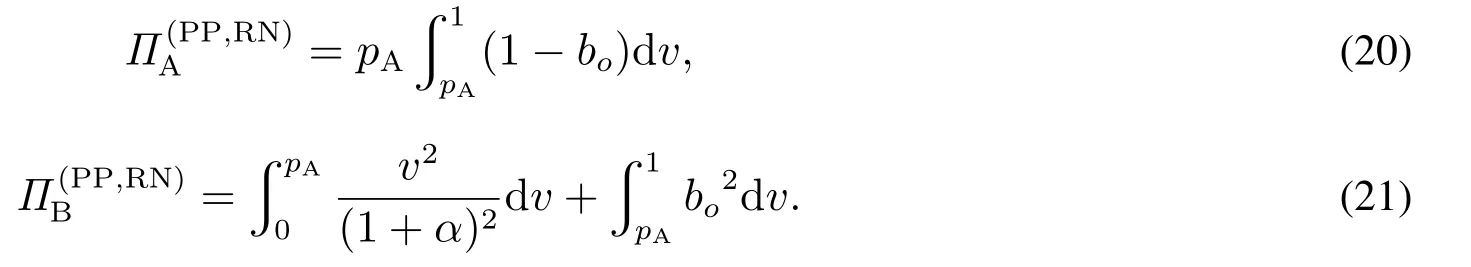
4.3 两家零售商均采用RN模式的情形
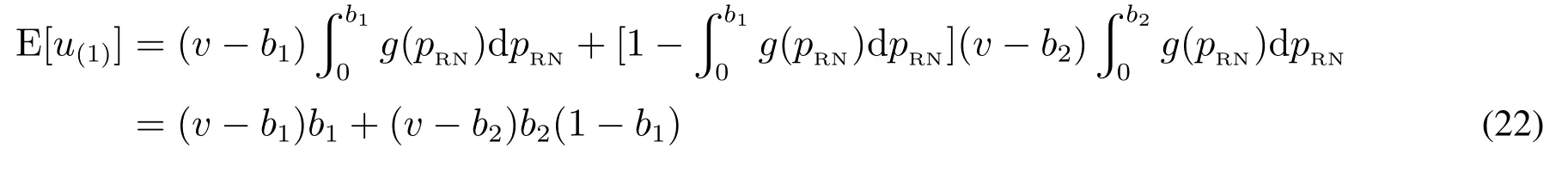
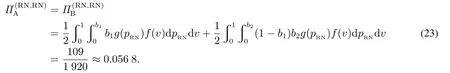
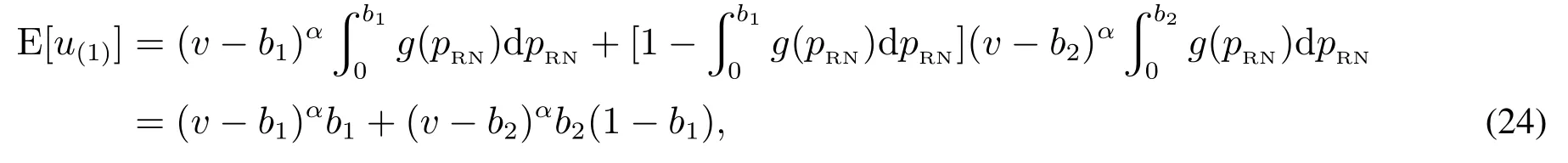
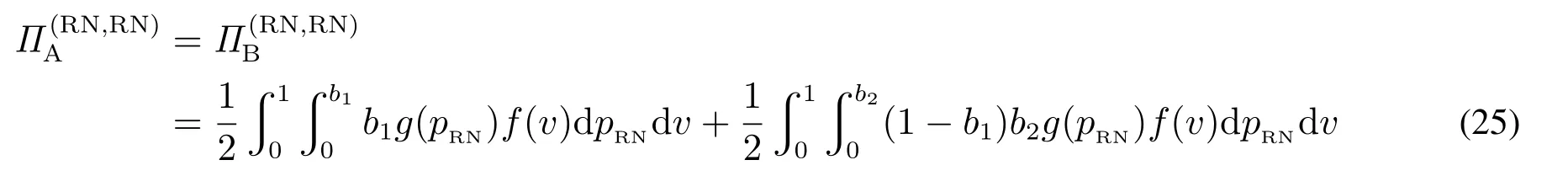
4.4 模式选择


5 结束语

