胶层厚度对多点支撑光窗面形的影响

孙冬明,潘 栋,刘宏旭,张天琦

(中国电子科技集团第十一研究所,北京 100015)

1 引 言

在光机结构装配中,黏合剂可以替代螺栓、压板等机械零件来实现紧固作用,与传统的机械紧固方式相比,黏结剂紧固方式具有结构简单、质量轻、装配应力分布均匀、柔性高等特点,随着现代制造工艺的发展,结构黏合剂的物理化学性能得到了大幅的提升,并在精密光机系统的装配中逐渐得到广泛的应用。

不同的胶层厚度,黏结工艺等都会影响光学元件的面形。Vyacheslav[1]等为了能够说明不同类型下胶结结构的性能特点,对环形胶层紧固结构进行了热应力和热变形分析；Christopher[2]等提出了一种不同以往的结构设计方法,能够对环形胶层粘接系统消除热应力；Robert[3]等为掌握方形胶结系统的应力性能变化,对由均匀方形胶固结的透镜系统进行了研究；李福[4]等从胶结结构的形状变化着手,分析得出圆形胶点要比方形胶点对反射镜的面形的影响小；赵伶丰[5]等为了解胶结接头对应力大小与分布的影响,对其结构进行了研究；Vlasenko[6]等对胶层厚度一致性控制进行了研究；Stubbs[7]等对胶层力学特性,如胶层黏结强度,胶层固化过程中的内应力等进行了研究；董德义[8]等分析了在温度变化的环境下通过控制胶层厚度消除或减小热应力。综上,在使用胶结方式支撑光窗的领域中,胶层厚度对于光窗的光学面形影响鲜有人研究。

本文以某型战斗机光雷保护罩采用的多点支撑光窗为研究对象,建立胶层连接的多点边缘支撑结构模型,分析胶层厚度对光窗面形变形的影响。该研究中所涉及的研究方法及结论,可为多点边缘支撑光窗过程中胶层厚度的确定提供参考。

2 光窗支撑形式

参考某型战斗机光雷系统保护罩可知,为了能够确保光窗位置精度和表面面形不受到破坏,采用压块多点边缘支撑光窗方式进行固定,简化模型如图1所示。在理想情况下,多点边缘支撑的光窗元件的受力变形情况如图1(b)所示。光窗在重力的作用和压块挤压力作用下,压块与光窗间的胶层厚度不同导致挤压力大小不同,同时光窗为非规则形状表面,导致光窗所受力不均,从而影响光窗的面形。

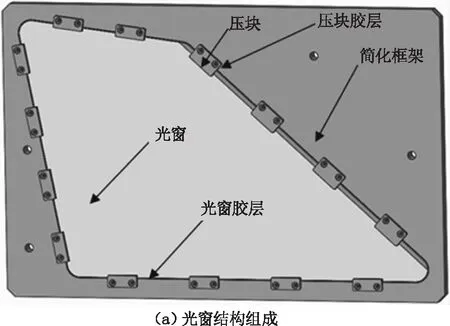
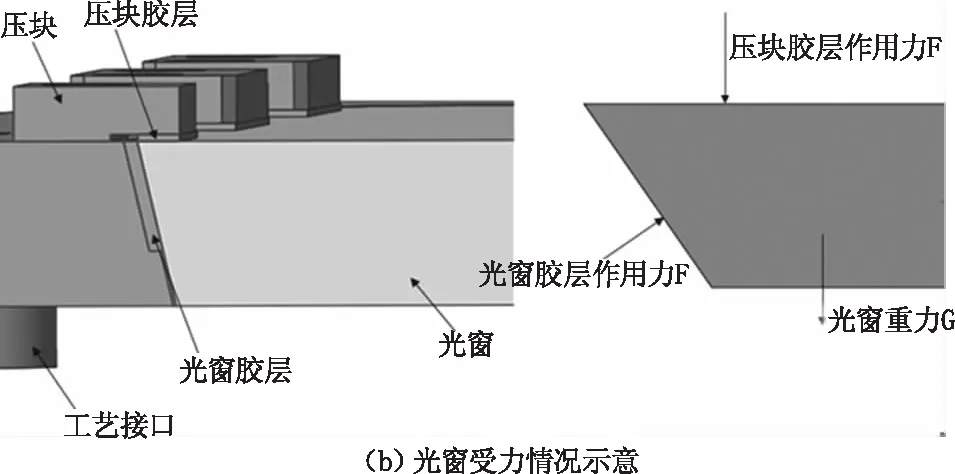
图1 多点支撑的光窗

3 面形质量评价

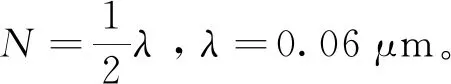
目前最为常用的面形评价方法是通过变形镜面表面上的点,相对于某一最佳拟合面的PV值和RMS值来评价面形[9]。通常使用Zernike多项式作为结构分析软件和光学设计软件之间的数据转换,从而进行光学系统性能的分析[10]。利用MATLAB软件编写最小二乘法的Zernike多项式拟合离散化的有限元光窗变形节点位移数据。拟合时Z轴与光轴方向相同,利用线性组合的方式,把光学波面用前N项Zernike多项式表示为[11]:

W((x,y)=a0+a1Z1(x,y)+…+anZn(x,y)+…+aNZN(x,y)

(1)

式中,an表示第n项Zernike多项式的系数。其中k=1,2,…,M为采样点,ZN(xk,yk)代表第n项Zernike多项式,通过极值法计算得Zernike多项式的系数:

(2)

将系数代回至式(1)可得拟合出来的面形表达式。Zernike多项式前三项所代表刚体位移量,令其为Rk,第k个节点光窗表面畸变的量为Dk=Wk-Rk。假设有限元计算得出M个节点的面形数据,令矩阵:

(3)

则根据PV值与RMS值的定义可以求出反应面形质量的参考量为:

PV=Max((s)-Min(s)

(4)

(5)

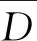
4 仿真计算

4.1 结构模型

将简化后的模型作为有限元分析的结构模型,其中模型包括框架,压块,压块胶层,光窗,光窗胶层。胶层属高分子材料,材料性质具有高度非线性性质,具有超弹性,在网格划分时,突出使用单元划分功能,将胶层在法向受力方向具有3阶网格结构,网格质量评估为0.8,如图2所示。压块胶层过厚,导致光窗支撑刚度不足且封胶工艺操作性差；压块胶层过薄,光窗与压块接触应力过高,有导致光窗破坏的危险。本文设定胶层厚度范围为0.1～0.5 mm,通过改变胶层厚度,分析光窗的受力变化及面形变化。

图2 多点支撑的光窗有限元模型

4.2 材料特性

材料模型对于仿真分析非常重要,图2中所涉及的材料主要特性如表1所示。表1中所列均为室温条件下的参数,因此本文仿真分析结果(除温度冲击试验)仅作为常温条件下的设计参考。

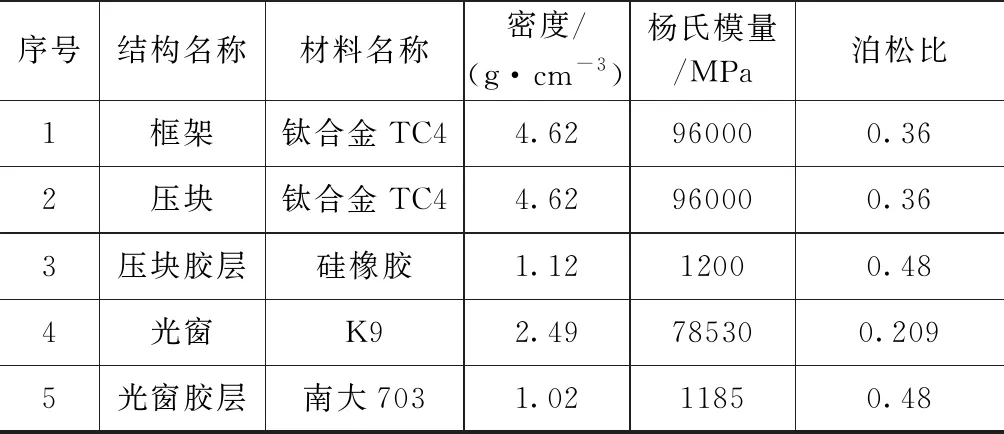
表1 材料特性

4.3 边界条件

简化模型各结构通过胶结和螺钉连接等方式进行连接,模型通过5个工艺接口固定连接在试验品台上。如图3所示。

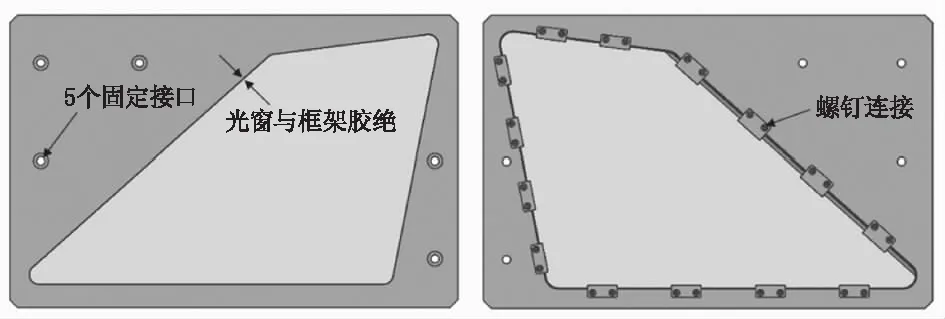
图3 多点支撑的光窗有限元模型边界条件

4.4 仿真条件

为了能够准确预测在战斗机多种运行环境下,胶层厚度不同对光窗作用力的变化和对光窗面形影响。本文根据国军标,结合某型战斗机的光雷保护罩提出的试验标准,分别制定了过载冲击仿真,随机振动仿真与温度冲击仿真。

4.4.1 过载冲击仿真

试验按照GJB150.15A-2009规定的内容,前向加速度1.5g,国军标中为安全起见,静力学载荷安全系数F=1.5,实际加载加速度为1.5g×1.5g。

4.4.2 随机振动仿真

随机振动载荷工况采取PSD G Acceleration形式,由于PSD也是一种响应谱,因此加载形式与谱分析完全一致,可在约束位置加载激励谱。为了保证随机振动计算结果的精度,模态分析的固有频率范围要大于PSD曲线频率范围的1.5倍。实验谱值按照GJB150.16A-2009中的规定进行施加。

4.4.3 温度冲击仿真

试验条件按照GJB150.5A中规定进行施加。

通过多参数仿真的方法,将胶层变化厚度设置为参数项,定义为P。改变参数P的数值大小,从而改变胶层厚度大小。参数P设置胶层厚度为0.1～0.5 mm范围内,研究胶层厚度对于光窗表面变形的影响。

4.5 仿真结果

4.5.1 过载冲击仿真结果

施加接触方式、约束和相应的加载条件,各个零部件赋予不同的材料属性。求解得到不同胶层厚度下光窗表面的变形和应力结果。以胶层厚度为0.5 mm,航向前向加速度为例,光窗表面变形使用等高线方式表示,分别在5倍变形和1倍变形下,反应了光窗表面的变形量和变形趋势。如图4所示。光窗应力如图5所示。

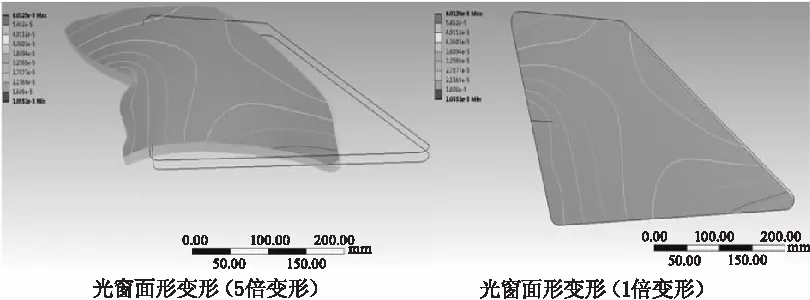
图4 光窗面形变化

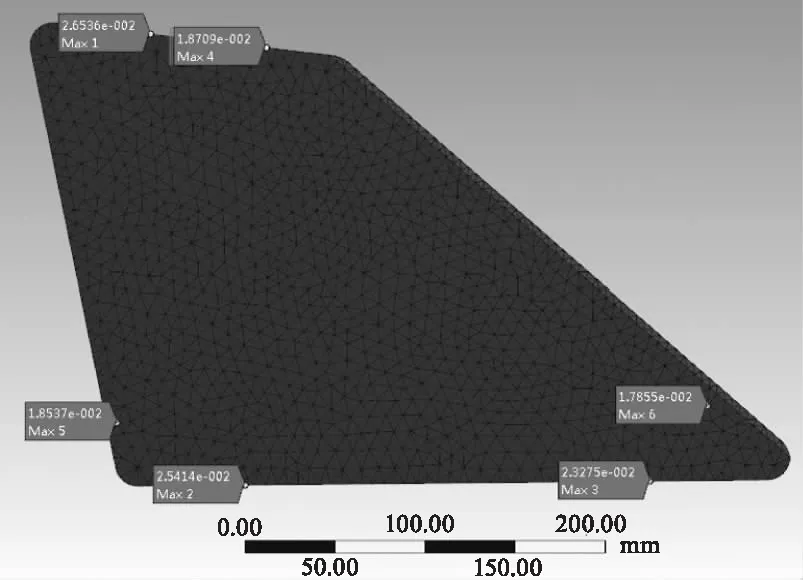
图5 光窗应力

对0.1～0.5 mm胶层厚度内光窗仿真结果进行分析,得到不同胶层厚度下光窗应力随胶层厚度变化的关系,如图6所示。提取仿真结果,得到光窗表面各节点的变形数据,编写结果数据处理方程获得节点位置数据。结合第3节提到Zernike多项式拟合工具与节点位置数据点,通过数据处理得到光窗面形的峰谷值PV和均方根值RMS。分别对0.1～0.5 mm胶层厚度内光窗节点位置数据进行分析,得到不同胶层厚度下光窗面形的PV值和RMS值,如图7所示。

图6 胶层厚度与光窗应力的关系

图7 不同胶层厚度下光窗面形的PV值和RMS值

4.5.2 振动仿真结果

以胶层厚度为0.5 mm为例,光窗变形如图8所示；光窗应力如图9所示。

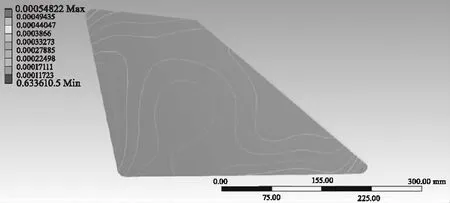
图8 光窗面形变化

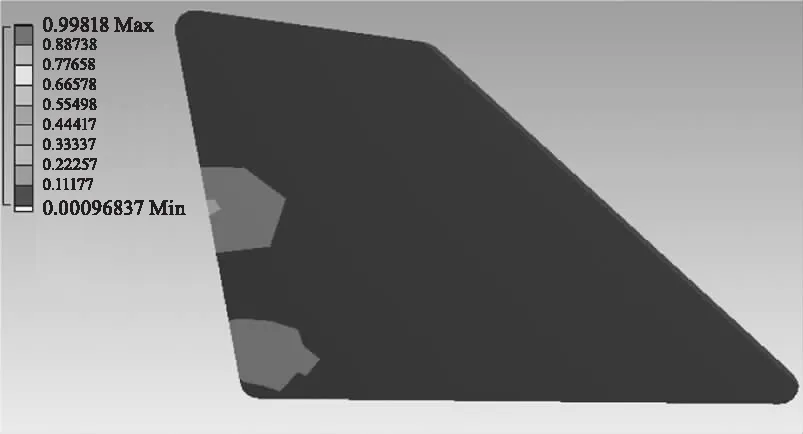
图9 光窗应力

对0.1～0.5 mm胶层厚度内光窗仿真结果进行分析,得到不同胶层厚度下光窗应力随胶层厚度变化的关系,如图10所示。分别对0.1～0.5 mm胶层厚度内光窗节点位置数据进行分析,得到不同胶层厚度下光窗面形的PV值和RMS值,如图11所示。

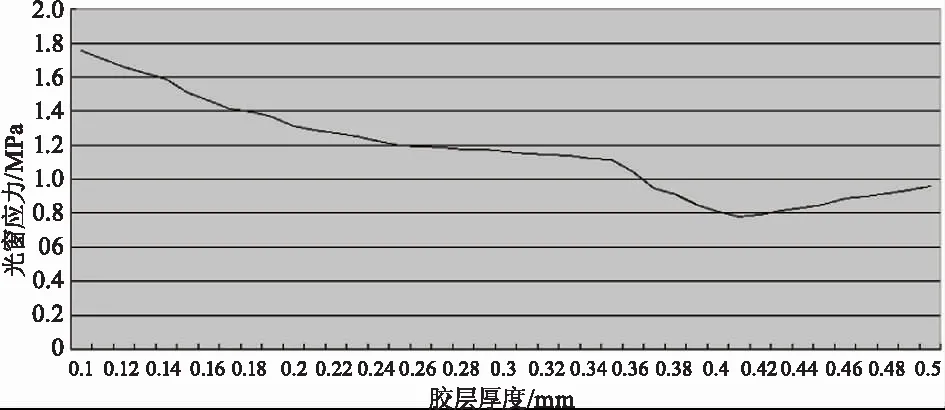
图10 胶层厚度与光窗应力的关系

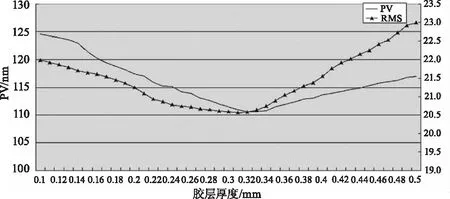
图11 不同胶层厚度下光窗面形的PV值和RMS值

4.5.3 温度冲击仿真结果

以胶层厚度为0.5 mm为例,光窗表面变形如图12所示。光窗温度场变化如图13所示。

图12 光窗面形变化

图13 光窗温度场分布

分别对0.1～0.5 mm胶层厚度内光窗仿真结果进行分析,得到不同胶层厚度下光窗应力随胶层厚度变化的关系,如图14所示。

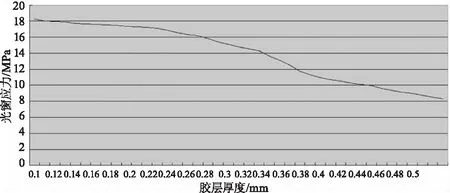
图14 胶层厚度与光窗应力的关系

分别对0.1～0.5 mm胶层厚度内光窗节点位置数据进行分析,得到不同胶层厚度下光窗面形的PV值和RMS值,如图15所示。

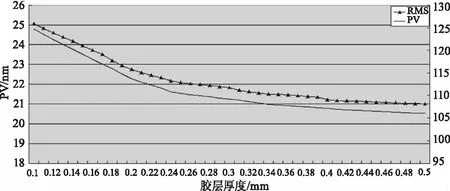
图15 不同胶层厚度下光窗面形的PV值和RMS值

5 仿真结果分析及结论

通过控制胶层厚度变化,固定结构、外界载荷、约束等边界条件,仿真发现:胶层厚度为0.1～0.5 mm范围内：

1)过载仿真试验中,光窗应力随着胶层厚度的增加,先减小后增大,在厚度值为0.33 mm时出现最小值；光窗面形的PV值和RMS值随着胶层厚度的增加先减小后增大,在0.46 mm胶层厚度处,出现最小值。

2)振动仿真试验中,光窗应力随着胶层厚度的增加,先减小后增大,在厚度值为0.41 mm时出现最小值；光窗面形的PV值和RMS值随着胶层厚度的增加,先减小后增加,在胶层厚度为0.32 mm时出现最小值。

3)温度冲击仿真试验中,光窗应力随着胶层厚度的增加而减小,且减小的速度随着胶层厚度增加而加快；光窗面形的PV值和RMS值随着胶层厚度的增加而减小。

对于本课题中出现的不规则多点支撑光窗,利用加速度过载、振动和温度冲击三种仿真试验,通过改变胶层厚度的方式,对比仿真结果可以确定胶层厚度对光窗面形有着不可忽略的影响。综合对比胶层在三个试验中对光窗面形的影响可知,胶层控制在0.18～0.5范围内对于各仿真试验下的光窗分辨率要求都能满足；在0.3～0.48范围内,光窗应力呈现低值状态；综合考虑应力状态和光窗表面变形情况,胶层在0.31～0.37范围内,光窗具有较好的力学状态和光学分辨率。