基于平行背光源的含内棱孔型零件定位方法

刘航铖，严小军，惠宏超

(北京航天控制仪器研究所，北京 100039)

引言

在精密自动装配过程中，机器视觉检测通过识别零件轮廓，进而确定轴孔零件中心的方法来实现零件的对位[1]，照明系统作为视觉检测的关键部分，对零件的轮廓的识别精度有显著影响。与常用的环形光源及线光源比较，平行背光源具有尺寸检测精度高，被测零件轮廓更为清晰等特点[2，3]，能有效提高机器视觉在精密装配领域中的检测精度。

但由于待装配的孔零件无法保证完全竖直，在孔零件存在不确定的小角度倾斜时，采用平行背光照明将出现的光路如图1所示，所成的像分别对应零件上下端面的轮廓，这将超出镜头允许的景深范围，导致无法采集到清晰的图像，使平行背光源在孔零件定位的工程应用中使用困难。

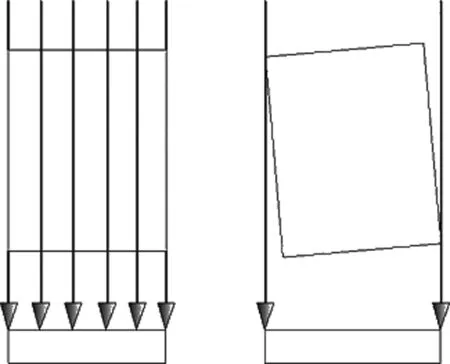
图1 零件倾斜时平行背光照明的光路Fig.1 The light path of parallel backlight when the parts are inclined

文献[4]在孔径尺寸检测中引入了平行背光源照明，但主要用于提高图像对比度，在轮廓识别中仍依靠环形光源正面照明。文献[5]中采用平行背光源照明突出零件轮廓特征，但检测对象为圆柱形零件的侧面轮廓，在零件倾斜时仍可获得清晰图像。文献[6]中利用平行背光源照明实现了机器视觉高精度检测，但其检测对象为球形体，无法适用于孔零件的定位检测。

图2 薄壁孔零件的内棱结构Fig.2 Inner edge structure of thin wall hole parts

针对上述问题，提出了一种基于平行背光源的孔零件定位方法，利用图2所示的孔型零件对安装轴起固定、限位作用的内棱结构，在零件倾斜导致光路被阻挡的情况下，相机通过采集零件内棱的轮廓特征来获取零件位置信息。分析了内棱轮廓的图像特征，并设计了对应的图像处理算法、零件倾斜角计算方法与空间定位方法，实现对孔零件的准确空间定位。该方法克服了平行背光源的工程应用困难，提高了机器视觉检测精度，在单目视觉条件下，可实现在孔零件倾斜角小于1°时，同轴度要求10 μm的轴孔自动化装配。

1 平行背光条件下视觉检测的可行域

相机需要采集到孔零件内棱的完整轮廓才能满足检测要求，因此，仅当平行背光覆盖范围包括内棱的全部边缘轮廓时，视觉检测系统才能获得内棱结构的完整图像。

图3 薄壁孔零件的简化模型Fig.3 Simplified model of thin wall hole parts

将薄壁孔零件简化为图3所示的模型，设零件沿轴线的倾斜角为β，内棱厚度为h，深度为L，长度为l，零件全高为H，内壁半径为r，据此可以给出倾斜角可行域的第一个条件，用以计算采用平行背光方式照明时，满足机器视觉检测要求的零件倾斜角极值：

(1)

同时，平行背光照明在相机镜头中所成的像是轮廓的阴影，如图4所示，由于倾斜，图像上所呈现的阴影轮廓实际上分别属于孔零件内棱的上下表面。

图4 平行背光在零件内部结果的实际投影轮廓Fig.4 The actual projection profile of the parallel backlight results inside the part

为满足图像清晰度需求，用于机器视觉检测的镜头需要在一定的景深范围下工作，设镜头工作的景深范围为±a，零件倾斜后的图像为上下两个轮廓阴影的拼接，因此两个轮廓的位置都需要满足工作距离的要求，在符合式(1)中倾斜角可行域的前提下，则可以得到倾斜角可行域的第二个条件：

(2)

2 图像特征

当零件端面与相机成像面不平行时，圆轮廓在相机中的成像为椭圆[7]，在图3所示的倾斜情况下，将上下表面轮廓分别简化为无厚度的薄壁，其在相机中的成像为两个椭圆， 因此，孔零件内棱在相机中的成像结果如图5所示，为两个椭圆各自的一部分拼接而成。

图5 孔零件内棱结构轮廓的投影Fig.5 Projection of inner edge structure contour of hole parts

设孔零件端面某点的坐标为[xw,yw,zw]，本文使用的镜头为远心镜头，可以避免成像远小近大的问题，根据变换原理，其在数字图像坐标系O-uv中的投影坐标为[8]：

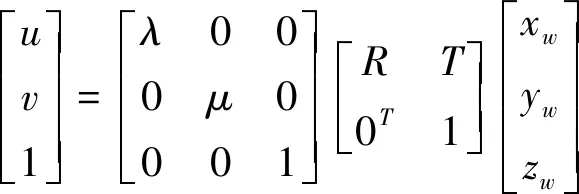
(3)

上式中矩阵λ,μ由镜头放大倍数与相机像元尺寸决定，是固定值，矩阵R、T由坐标系变换决定，为便于研究，以孔零件竖直固定时，固定面圆心为原点，圆柱轴线为Z轴建立如图6所示的直角坐标系。在该坐标系下，零件的倾斜总可以分解为绕X轴旋转与绕Y轴旋转，因此假定零件仅绕X轴旋转来对图像特征进行研究。

图6 零件装配坐标系Fig.6 Part assembly coordinate system

零件的定位问题可以转化为在二维图像中寻求适宜的关键特征，继而设置相应的定位算法，使零件得以实现成功装配。在假定零件仅绕X轴旋转的前提下，可对孔零件的图像特征分析如下：

1)设未发生倾斜时，孔零件内棱下表面与X轴平行的直径，其与内棱外壁的交点在世界坐标系中的坐标分别为A(x1,0,z1)，B(-x1,0,z1)，则在零件绕X轴旋转β后，A、B的坐标分别变为:

A(x1,(H-L)sinβ,z1-(H-L)tanβsinβ)

(4)

B(-x1,(H-L)sinβ,z1-(H-L)tanβsinβ)

(5)

2)设未发生倾斜时，孔零件内棱下表面与Y轴平行的直径，其与内棱外壁的交点在世界坐标系中的坐标分别为C(0,y2,z2)，则在零件绕X轴旋转β后，C、D的坐标分别变为：

C(0，y2+[r(1/cosβ-1)+(H-L-rtanβ)sinβ],

z2-f(β))

(6)

D(0，-y2+[r(1-cosβ)+H-L]sinβ,z2-f(β))

(7)

3)根据式(3)给出的变换原理，通过调整相机位置使R为单位矩阵，T为0矩阵，若将孔零件内棱视为无厚度的薄壁，可以得到，在相机获取的内棱下表面图像中，A、B、C、D点对应的坐标分别为：

A1(x1λ,(H-L)sinβμ)

(8)

B1(-x1λ,(H-L)sinβμ)

(9)

C1(0,{y2+[r(1/cosβ-1)+(H-L-

rtanβ)sinβ}μ])

(10)

D1(0，{-y2+r(1-cosβ)+(H-L)sinβ}μ])

(11)

同理可以分析得出，若将孔零件内棱视为无厚度的薄壁，则上表面相同位置的点在零件倾斜后，在相机获取的图像中的坐标为：

A2(x3λ,(H-L-h)sinβμ)

(12)

B2(-x3λ,(H-L-h)sinβμ)

(13)

C2(0,{y4+[r(1/cosβ-1)+(H-L-h-

rtanβ)sinβ}μ])

(14)

D2(0，{-y4+r(1-cosβ)+(H-L-h)sinβ}μ])

(15)

由以上坐标变化结果可知，当零件绕X轴旋转时，孔零件内棱同一表面上，与X轴平行的直径与内棱外壁的交点在相机采集的图像中，沿X轴方向的坐标值之差始终为2λx1=2λr，与倾斜角度无关；与Y轴平行的直径与内棱外壁的交点在相机采集的图像中，其沿Y轴方向的坐标值之差为2rcosβμ，与倾斜角度相关。

由此可知，绕X轴倾斜后的孔零件内棱同一表面在相机中成像的椭圆特征为：长轴长度为内棱半径的整数倍且保持不变，短轴长度与倾斜角β及内棱的半径r相关。因此，相机最终采集到的图像为上下表面所成像的两个相同椭圆的拼接，为实现定位，需对采集到的椭圆图像进行拟合。

3 零件的空间定位

3.1 椭圆拟合算法

椭圆拟合较常见的方法主要为hough变换拟合[9]与最小二乘法拟合[10]两种方法，但直接使用这些方法进行拟合时，其计算效率与轮廓识别误差难以满足精密装配的需要。针对孔零件的实际特征，采用优化后的椭圆拟合算法[11]，结合归一化与最小二乘法对椭圆进行拟合，得到式(4)中的椭圆参数A、B、C、D、E、F：

Ax2+Bxy+Cy2+Dx+Ey+F=0

(16)

则椭圆中心坐标(xc,yc)为：

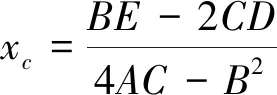
(17)

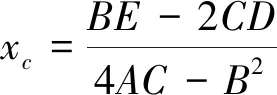
(18)

短轴长度b为：

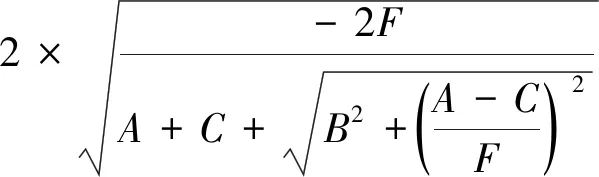
(19)

3.2 零件倾斜角的确定

如前文所述，倾斜孔零件的内棱在空间中的投影为两个相同椭圆的拼接，且椭圆短轴在数值上仅与孔零件内棱半径r及倾斜角度β有关，因此可建立函数f(β)=rcosβ=b，通过拟合出的b值解出β值：

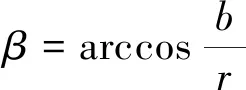
(20)

函数f(β)=rcosβ为偶函数，因此经上述方法计算出的倾斜角将有两个解，这是圆的二义性问题[12]，当零件绕同一个轴旋转±β时，所得到的椭圆投影是一致的。

针对这一问题，一般通过零件连续运动或采集不同位姿下的两幅视图，确定零件的倾斜角的唯一解[12，13]，但孔零件的夹持机构只有线位移自由度，无法实现偏转角度的连续变化。因此利用文献[14]所述的分光棱镜改变光路，使相机可在零件侧面采集到零件端面图像，撤去分光棱镜后，相机可对孔零件侧面轮廓进行拍摄，通过以下方法判断倾斜方向，得到倾斜角的唯一解：

1)如图7所示，当零件沿X轴旋转时，相机拍摄孔零件的侧面特征，当侧面底部轮廓特征能观测到两段圆弧时，零件逆时针旋转，反之顺时针旋转；

2)当零件沿Y轴旋转时，相机拍摄孔零件柱面的侧面特征，通过侧面直线的偏斜方向确定旋转方向；

3)零件的倾斜可以分解为绕X、Y轴的旋转过程，因此在完成上述检测后，零件的倾斜角即可得以确定。

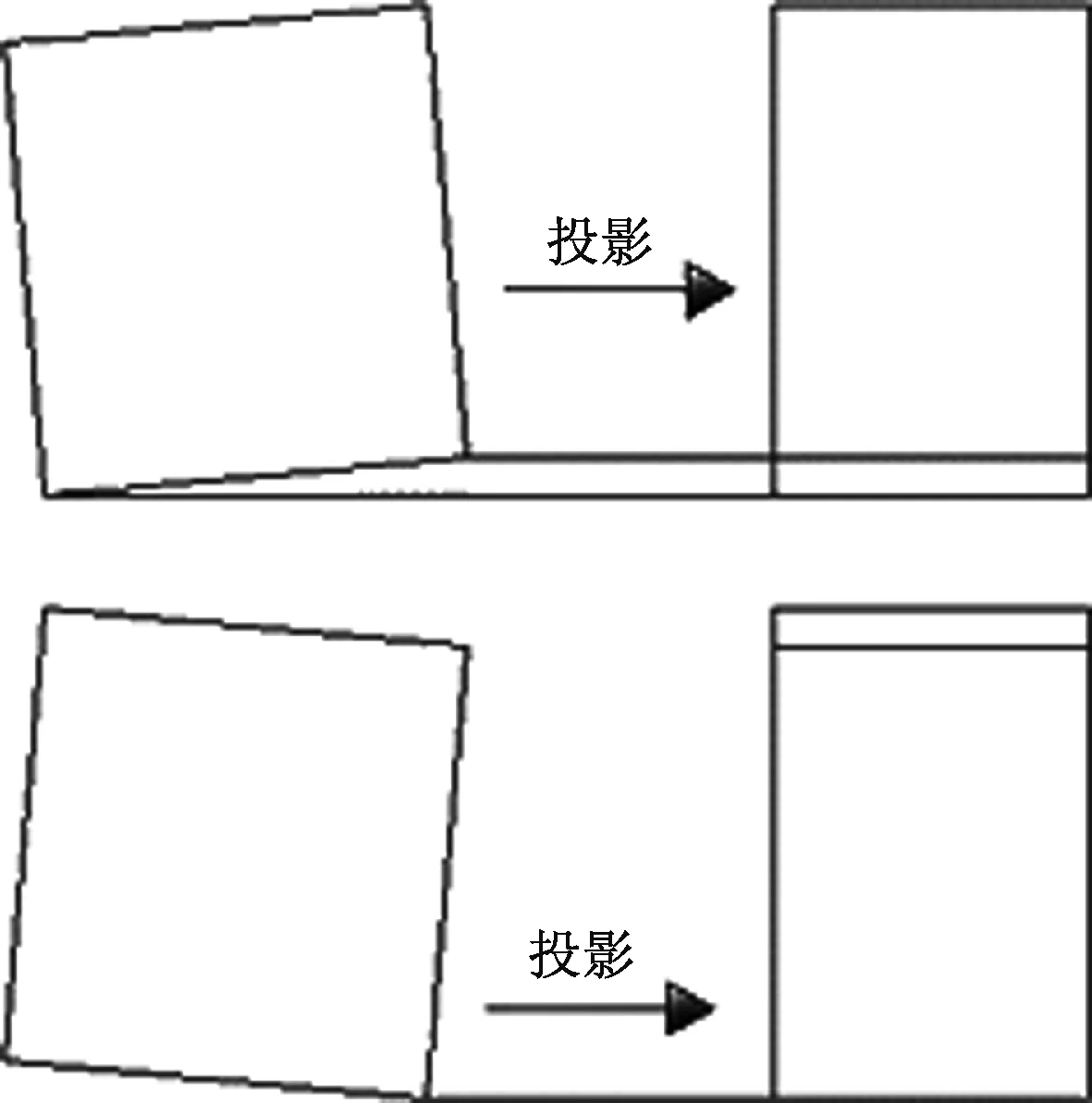
图7 零件沿不同方向旋转同一角度时的不同投影Fig.7 Different projections of parts rotating in different directions at the same angle

3.3 零件的空间位置

孔零件图像为两个椭圆的拼接，其图像中心点坐标为两个椭圆中心点连线的中点：

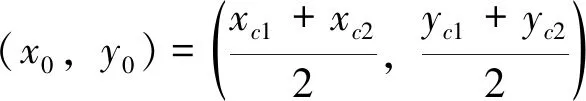
(21)

以孔零件装配坐标系为世界坐标系，根据远心镜头坐标变换规律，零件端面中心点的坐标为：

(22)

同时，零件在空间中的倾斜角为β也已计算得出。由此，孔零件在空间中的位姿可以完全确定。

4 方法的实际验证

4.1 倾斜角检测精度验证

待装配孔零件长40.00 mm，外径30.00 mm，内棱直径20.02 mm，圆柱轴零件厚度12.00 mm，半径20.00 mm，同轴度要求为10 μm，使用6 500万像素工业相机，其在平行背光条件下采集到的图像如图8所示。

图8 孔零件在平行背光条件下采集的图像Fig.8 Image acquisition of hole parts under the condition of parallel backlight

根据验证需求，将轴类零件与六自由度调整机构相连接以搭建装配平台。实验通过给定偏转角度的方式进行，在给定偏转角度后通过实验验证倾斜角计算方法的准确性，验证结果如表1所示。

表1 平行光源照明时倾斜角检测方法验证结果Table 1 Verification results of tilt angle detection method for parallel light source illumination

实验显示，本文提出的倾斜角检测方法绝对精度小于0.002°，相对误差小于0.5%。

为验证本文方法对装配精度的提升，使用环形光源进行正面照明，以孔零件端面为检测对象，采用同样的方法检测倾斜角度，其结果如表2所示。

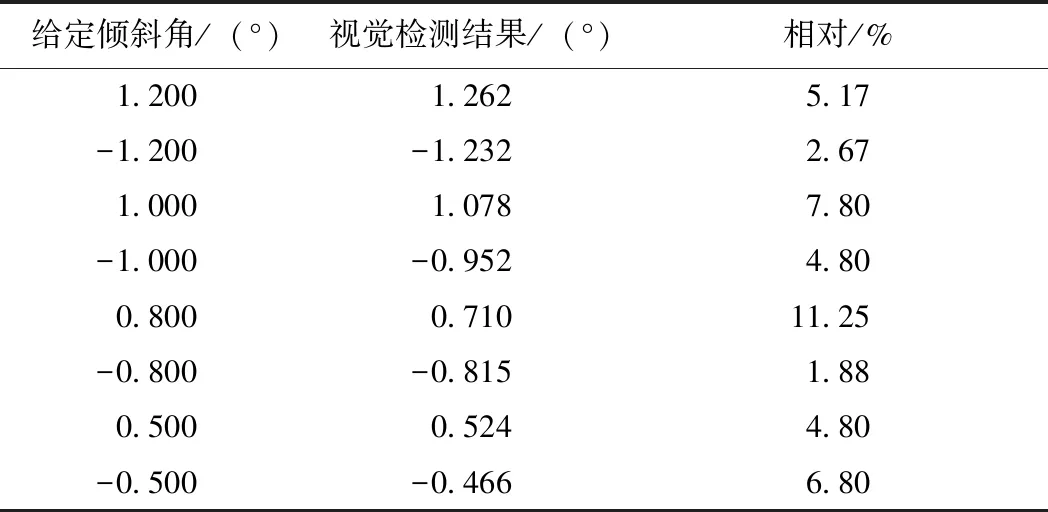
表2 环形光源照明时倾斜角检测方法验证结果Table 2 Verification results of tilt angle detection method for annular light source illumination

可知，在给定同样倾斜角的情况下，采用平行背光源时，倾斜角检测精度明显优于环形光源正面照明，证明本文提出的利用平行光源背光照明检测倾斜角的方法能有效提高机器视觉检测的精度。

4.2 装配效果验证

根据以上所述的定位方法进行零件装配，试装配中，通过观察待装配零件在装配过程中是否出现卡阻来验证定位方法的可行性，采用同一套零件反复试装三十次，并与采用环形光源正面照明时的成功率进行对比，其结果如表3所示。

表3 不同照明方式下的装配成功率Table 3 Assembly success rate under different lighting modes

从上述实验结果可知，采用本文提出的精密定位改进方法后，待装配零件的一次装配成功率得以大幅提高，证明本文所提出的方法能在工程中得以实际应用。

5 结论

本文针对孔零件视觉定位过程中，在零件存在小角度倾斜时，平行光源工程使用困难的问题，利用孔零件内棱设计了一种改进后的视觉定位方法，可通过单目视觉的方式确定零件的倾斜角度并给出视觉定位特征点，最终实现孔零件的精确定位。

实际验证表明，本文提出的精密定位改进方法误差优于0.5%，解决了平行背光源在实际工程应用中的使用困难，与传统环形光源方案相比，装配精度与成功率均得以提升，改善了实际装配环节的质量，能够实现同轴度要求10 μm级的精密装配，具有显著的工程应用价值。