基于非成像数字光场理论设计的一种节能型壁挂式植物生长灯
赵 亮, 岑松原
(1.中国计量大学光学与电子科技学院,浙江 杭州 310000;2.杭州星野光学科技有限公司,浙江 杭州 310000)
引言
植物生长灯具有调节作物生长周期、延长光合作用时间、加速光合作用的作用,最终能够实现作物增产增质、提前上市的目的,是实现我国智慧农业、现代农业的重要一环[1]。近年来植物补光灯需求越来越强烈。传统的植物生长灯大多是直接通过LED的排布和灯之间的排布来实现简单的配光,由于灯具缺乏对光场的精确控制,通常只能通过增加灯具数量、缩短布灯距离等方式实现作物种植面上的光能高均匀度。这种相对简单的布灯方式易于造成光照不均匀和光能浪费,若要使得种植区域都达到一定的PPFD,传统方案往往只能通过增大功率或者把植物生长灯排的更密来实现,无论哪种方案都会大大增加成本,并且安装也十分不便,同时由于大棚没有预留安装位置,因此困难的安装方式和过多的灯具数量造成的初期一次性投入成本过高是限制植物生长灯在大棚中推广使用的重要原因。
经过市场调研,山东大量的暖棚因其特殊结构,使传统的植物生长灯难以满足要求。本文针对暖棚应用数字光场理论设计了一款壁挂式植物生长灯,解决了上述光照不均匀、安装困难和灯具数量较多的问题,以更低的成本、方便的安装和更好的效果为在普通大棚中推广使用植物生长灯创造了可能。
1 非成像数字光场理论的定义
非成像数字光场理论即通过抽象出光学系统中光场分布的基本单元(如图1所示),用数字化离散化的方式建立非成像数字光场函数NDLFF(Non-imaging digital light field function)来描述光学系统的理论。

图1 (a)三维光场单元模型;(b)二维光场单元模型Fig.1 (a)Illustration of 3D light field; (b)Illustration of 2D light field
要完整地描述非成像光学系统中的光场模型需要以下特征值:dA位置坐标p(x,y,z),dA面法线向量N(x,y,z),光锥方向向量Vθ(x,y,z),光锥与面法线的夹角θ,dA两侧的折射率n1和n2;简化成二维情况为:dl位置坐标p(x,y),dl面法线向量N(x,y),光锥方向向量Vθ(x,y),光锥与面法线的夹角θ,dl两侧的折射率n1和n2。
非成像数字光场函数NDLFF可以表示为
F=F(p,N,Vθ,θ,n1,n2)
(1)
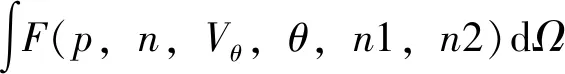
(2)
由边缘光线的基本内容可知:光源的边缘光线经过一个光学系统,以边缘出射光线出射到目标面,而在边缘光线内部的光线依然保持在内部出射到目标面,所以设计非成像光学系统时,通过非成像数字光场函数描述光场时,只需要考虑边缘光线,这就大大简化了数字光场函数NDLFF。另一方面,光学扩展量的三维微分形式[2]可以写成
dU=n2dAcosθdΩ
(3)
由式(3)数字光场单元模型也是光学扩展量的基本单元,那么已知光学系统空间的NDLFF分布也就得知了空间光学扩展量的分布,因为光学扩展量和光通量[3]存在如下关系
Φ=LU
(4)
其中Φ表示光通量,L表示亮度,U表示光学扩展量。又因为在朗伯光源的非成像光学系统中亮度守恒,L为定值,所以数字光场单元模型的光通量正比于光学扩展量。当按照dA相同大小并且足够小的离散化处理数字光场单元模型时,那么由dA构成面上光通量Φ的分布即可以作为照度分布。这样,通过非成像数字光场理论把原本抽象的光场分布用简单数学公式表示出来,可以更加精准地设计透镜。
2 应用数字光场理论的透镜设计
2.1 确定初始条件
山东暖棚截面示意如图2所示。土墙高度一般为3~4 m,种植区远端离土墙边距离一般为12 m,由于这些传统暖棚都没有预留安装植物灯的位置导致加装植物灯十分麻烦;另一方面,即使加装了传统的植物生长灯,由于其对配光的缺失,将会导致PPFD不均匀,因此针对上述情况,为了实现安装方便又均匀度高的目标,本文提出了一种壁挂式植物生长灯透镜方案。方案示意图如图3所示。

图2 暖棚截面示意图Fig.2 The cross-sectional diagram of the warm shed
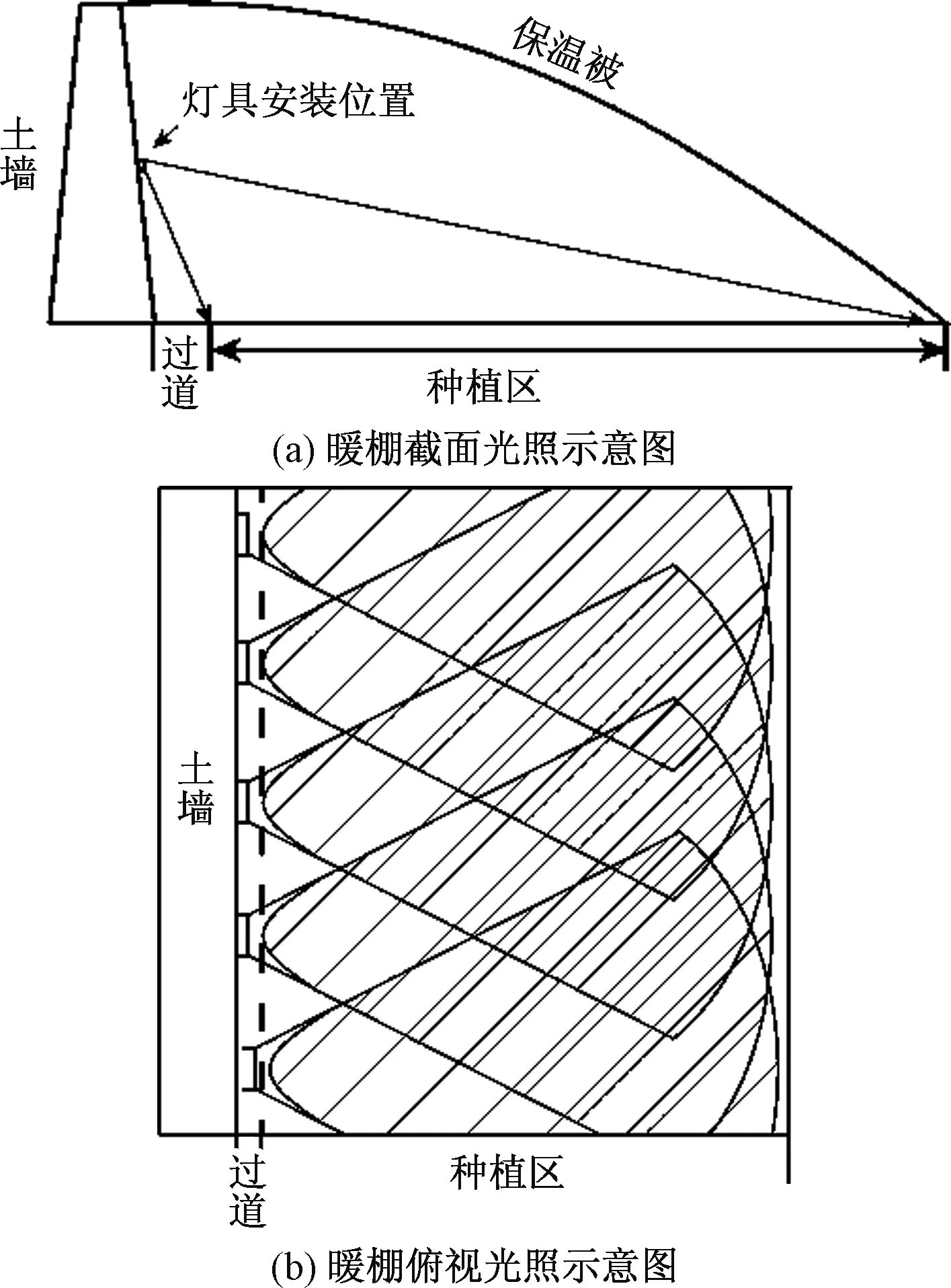
图3 (a)暖棚截面光照示意图;(b)暖棚俯视光照示意图Fig.3 (a)The cross-section illustration of the lamp installation;(b)the top view of the lighting overlapping distribution in the warm shed
由图3(a)所示,为了使安装方便,安装高度定为2 m,照射宽度达12 m,距高比为6∶1。由于其超高距高比,透镜偏折光会非常厉害,所以选用两片透镜的方案,第一片透镜为旋转对称结构,第二片为柱形结构,这样可以在保证效果的情况下,节省原料,降低注塑难度,从而大大降低注塑成本。由图3(b)所示,种植区离灯具近的一侧光斑无叠加,随着距离增大光斑叠加数量增多,所以在设计单灯照射区域时要考虑叠加情况,近端照度目标值大,远端相对减小。
2.2 计算自由曲面离散点
实际设计透镜时三维数字光场函数太过复杂,往往可以通过离散化二维数字光场函数加上反馈优化的方式简化计算。计算过程由计算机完成,因此离散化的二维数字光场函数用数组表示。
2.2.1 构造光源二维数字光场函数
金石滩码头入口附近有两棵老榆树,都一搂粗细,一些到这儿旅游的人正忙着在树下拍照。付玉穿着一身杉杉牌的西装,挎着一个大包,站在那儿摆弄手机。她比三年前更有风度,有魅力。
光源的光学扩展量可以表示为
U=π·n2·sin2(θ)·A
(5)
其中n表示折射率,θ表示出射半角,A表示LED出射面积。光通量可以表示为
Φ=L·U
(6)
其中L为发光亮度。把式(5)代入式(6)可得:
Φ=L·π·n2·sin2(θ)·A
(7)

利用数字光场理论建立的光源模型如图4所示。

图4 光源模型Fig.4 The light cone model of the light source
离散化数字光场函数可以表示为

(8)
psn表示第n小段光源的中心坐标,Nsn表示第n小段光源的法向量,Vsn表示第n小段光源出光光锥的中心方向向量,ns1、ns2分别表示光源前后的折射率。
2.2.2 构造曲面二维数字光场函数
通过分析可得,第一个面的作用是收束,曲线一的设计目标可表示为V=V(x),其中x=1,2,3,…,n,表示曲线离散化的序号,离散化数字光场函数可以表示为

(9)
第二个面的作用是在第三个面上重新分配光能,曲线2的设计目标可表示为Gc2=G(N(x),V(x),θ(x)),其中x=1,2,3,…,n,表示曲线离散化的序号。离散化数字光场函数可以表示为

(10)
第三个面设计为平面,光场传输到第三个面形成离散化数字光场函数Fc3,形式与式(9)和式(10)相同。
第四个面的作用是在目标面上重新分配光能,曲线四的设计目标可表示为Gc4=G(N(x),V(x),θ(x)),离散化数字光场函数Fc4,形式与式(9)和式(10)相同。
2.2.3 计算曲面二维离散化数字光场函数
首先计算曲线1二维离散化数字光场函数,其计算方法如图5所示。

图5 曲线1构建二维离散化数字光场示意图Fig.5 The method to construct an numerical illumination light field
图5表示简化的曲线1构建二维离散化数字光场示意图,以光源中心为原点建立直角坐标系,由于曲线1为旋转对称结构,所以以对称轴Y处P1点作为曲线1起点,法线N作为P1点的初始法线方向,图中清楚的展示只取三点为例。由光源二维离散化光场函数Fs可得,P1点的左右入射光线分别为LI和RI,根据折射定律可以计算出左右出射光线LO和RO,改变P1点法线方向就能改变左右出射光线LO和RO的方向,由左右出射光线LO和RO的方向就可以得到光锥中心方向V和光锥半角θ,这样P1点光场函数建立完成,再根据曲线1对应的映射关系调整P2,P3,…,Pn点的法线方向,这样完成了曲线1二维离散化数字光场的构建。
计算曲线2二维离散化数字光场函数,其计算方式与曲线1相同,不同的是映射关系,示意图如图6所示。
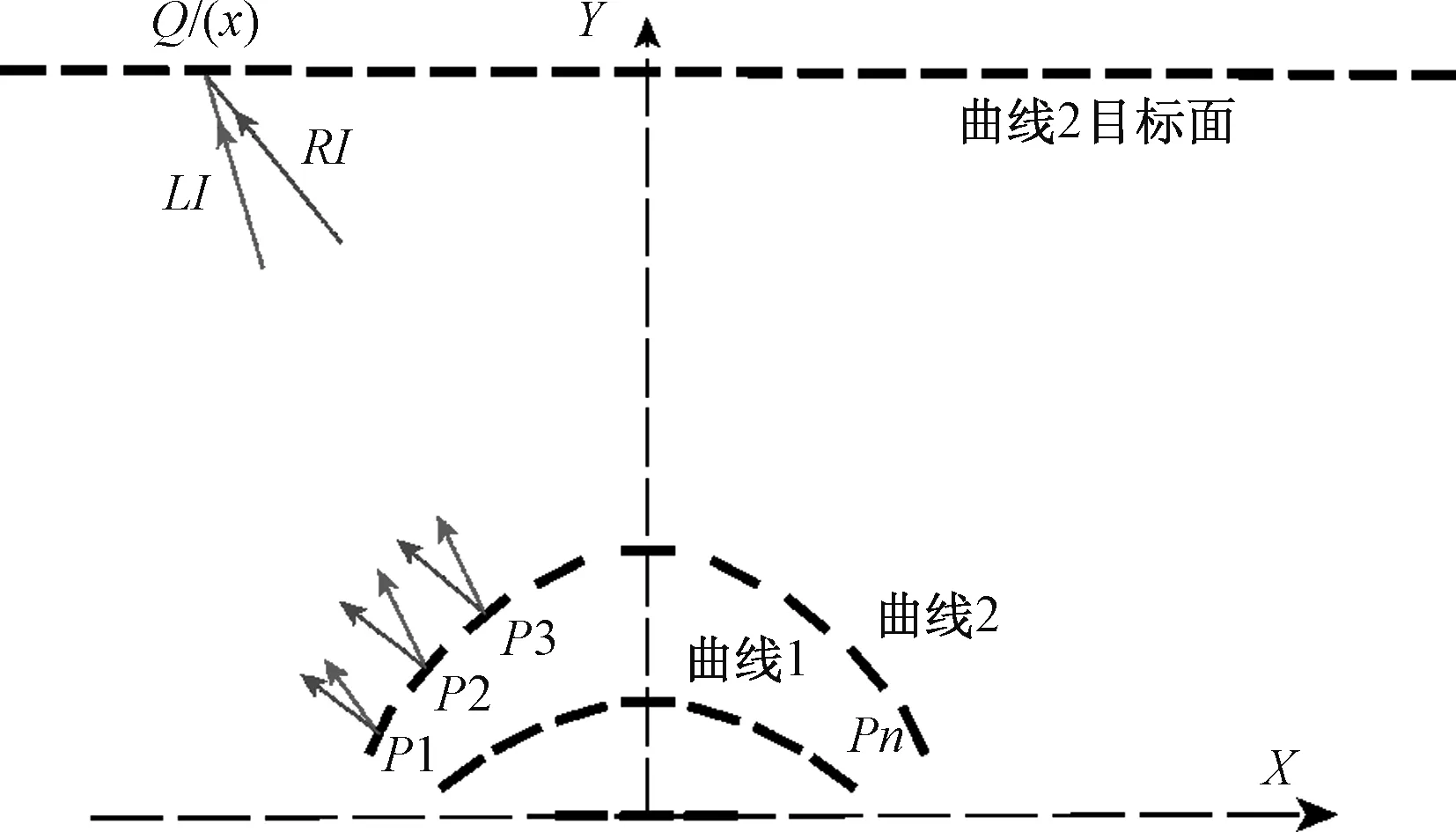
图6 曲线2构建二维离散化数字光场示意图Fig.6 The method to construct a target light field by free-form surface lens
图6表示简化的曲线2二维离散化数字光场构建示意图,在曲线3所在位置建立曲线2的目标面,预设目标面的照度分布值,由式(6)可知,照度正比于光学扩展量,而光学扩展量又由左右入射光线决定,以目标面上任意点Q为例,通过追迹曲线2的光线,可以得到Q点的左右入射光线LI和RI,即可得到该点的光学扩展量,改变曲线2二维离散化数字光场函数就能改变Q点的左右入射光线LI和RI,从而调整Q点的扩展量使其达到预设值。同样的方法把目标面上的扩展量分布调整为预设值,就得到了曲线2二维离散化数字光场函数曲线的产生方式相互类似,都是首先通过设定目标数值光场的分布,然后通过优化算法,计算曲线上的各离散点的坐标,使光线通过该曲面后形成目标的光场分布。
3 实例和分析
将计算得到的曲线导入3D建模软件建立实体模型,如图7所示。将模型导入光学仿真软件,如图8所示。参数设置如下:材料设置亚克力(PMMA),光源使用2835方杯,安装高度2 m。由于计算曲线时光场函数由三维简化为二维带来误差,导致实际仿真结果与设计目标产生偏差,需要根据仿真结果重新调整目标面的光场函数,反馈调节几次,就能得到一个理想的结果。最终仿真结果如图9所示。

图7 (a)透镜1;(b)透镜2Fig.7 The 2 lens used in the plant growth lamp

图8 左右边缘光线光路图Fig.8 The ray fan pattern of the optical system
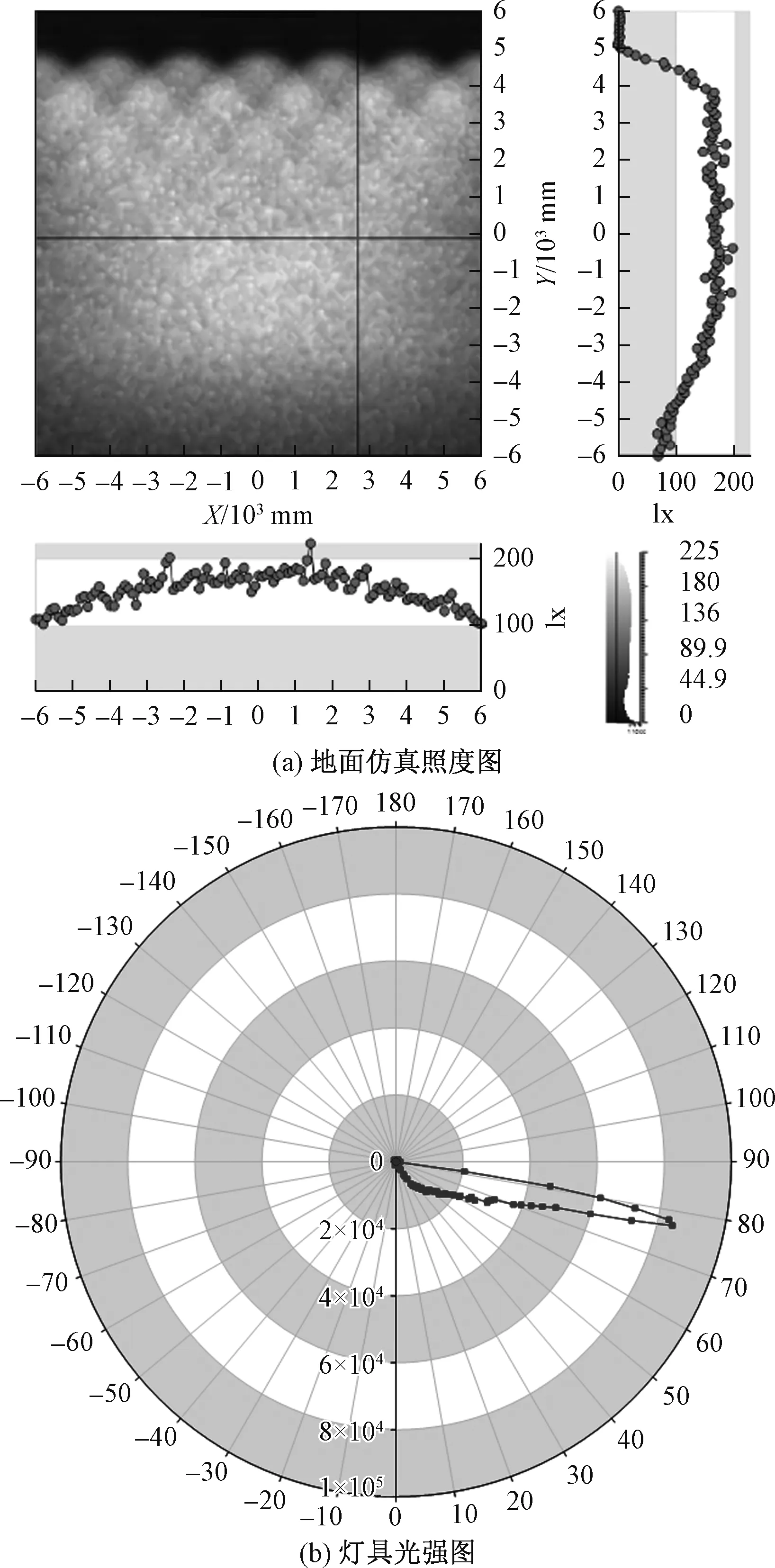
图9 (a)地面仿真照度图;(b)灯具光强图Fig.9 (a)The illuminance distribution of the ground in the warm-shed;(b)the light intensity of the lamp
从图9(a)的仿真结果得出在2~9 m范围内均匀度高达90%以上,在9~12 m范围内照度均匀度有所下降,光能利用率达到85%以上,整体效果对于一款植物生长灯而言满足需求。图9(b)表示其空间光强分布图,可知大角度的光强大,小角度的光强小,正是由于其特殊的光强分布,才能实现其超高距高比的照明要求。

图10 山东黄瓜暖棚试验情况Fig.10 The illumination effect in the warm-shed
图10是样灯安装在山东黄瓜暖棚中的使用情况,从图中可以看出其效果满足预期。其优势相比于其他补光灯有以下几点:1)安装方便,一方面大大降低一次性投入成本;另一方面可随着作物生长及时调节灯具高度,使其始终保持在最佳照射距离,从而光能利用最大化; 2)利用非成像数字光场理论的设计的透镜保证了其高均匀度和高光效,从而实现作物均匀生长。
4 结语
针对目前暖棚没有一款合适的植物生长灯的问题,提出了一套全新的理论:非成像数字光场理论,利用该理论设计了一款超高距高比壁挂式植物生长灯,均匀度在2~9 m范围内高达85%以上,在9~12 m范围内照度有所下降,光能利用率高达90%以上,解决了安装困难、均匀度低和灯具成本高等问题,并且实际批量生产样灯于大棚中试验,试样情况达到预期。在后续工作中将针对大棚远端照度有所下降问题持续改进优化。

