四阶热传导方程解爆破的一个新条件

熊梓伶， 杨 晗

（西南交通大学 数学学院，四川 成都611756）

由上面的综述知道，文献［1-3］中解的爆破准则不一样，文献［1，3］是考虑解的L2范数的破裂，文献［2］则是研究了解的时空范数的破裂，文献［4］的爆破条件与文献［1-3］有所不同，对非线性项的要求文献［4］的结论更深刻，它与对应的特征值问题有关.基于以上思想，本文主要结合特征值，利用Galerkin方法和凸性方法，研究方程解的存在性和一类新的爆破条件.

本文主要结论如下.

定理1 函数u满足条件

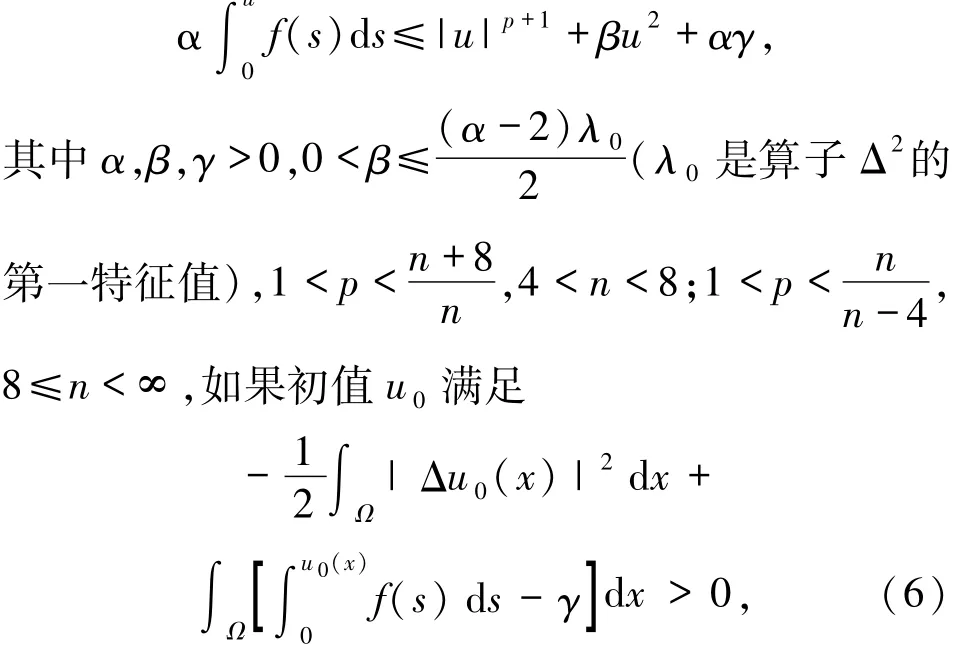
则对于原方程的解u在有限时间T满足

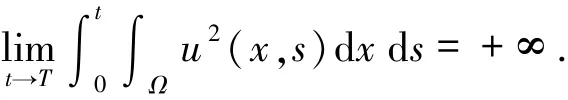
1 局部解的存在性

定理1.1 当u0∈H20时，方程组（1）存在局部解u满足

且

本文利用Galerkin方法证明解的存在性.在H20（Ω）中选择一组基础函数wj（j∈N），wj是满足以下Dirichlet边界条件的Laplacian算子的特征函数

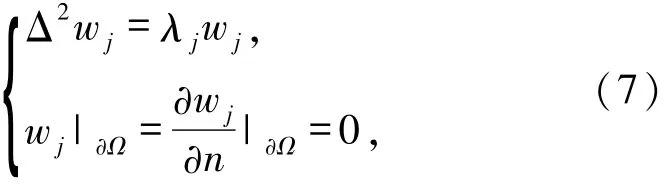
其中‖wj‖L2＝1.

1）构造近似解.对给定的正整数m，记

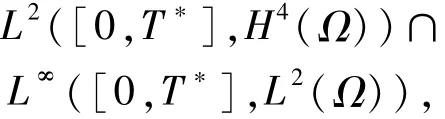
且

2 主要定理的证明

时，可得

其中

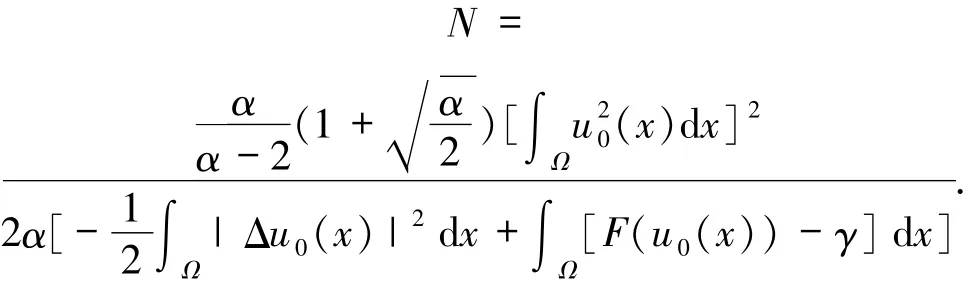
由于J（0）＞0，N＞0，可得

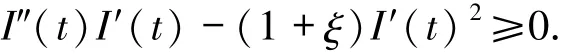
爆破时间T满足

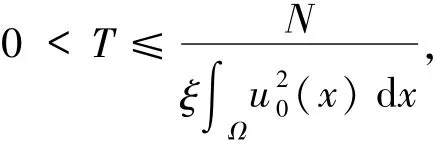
也就是说，当t≥0时，解u（x，t）在时间趋于T时爆破.