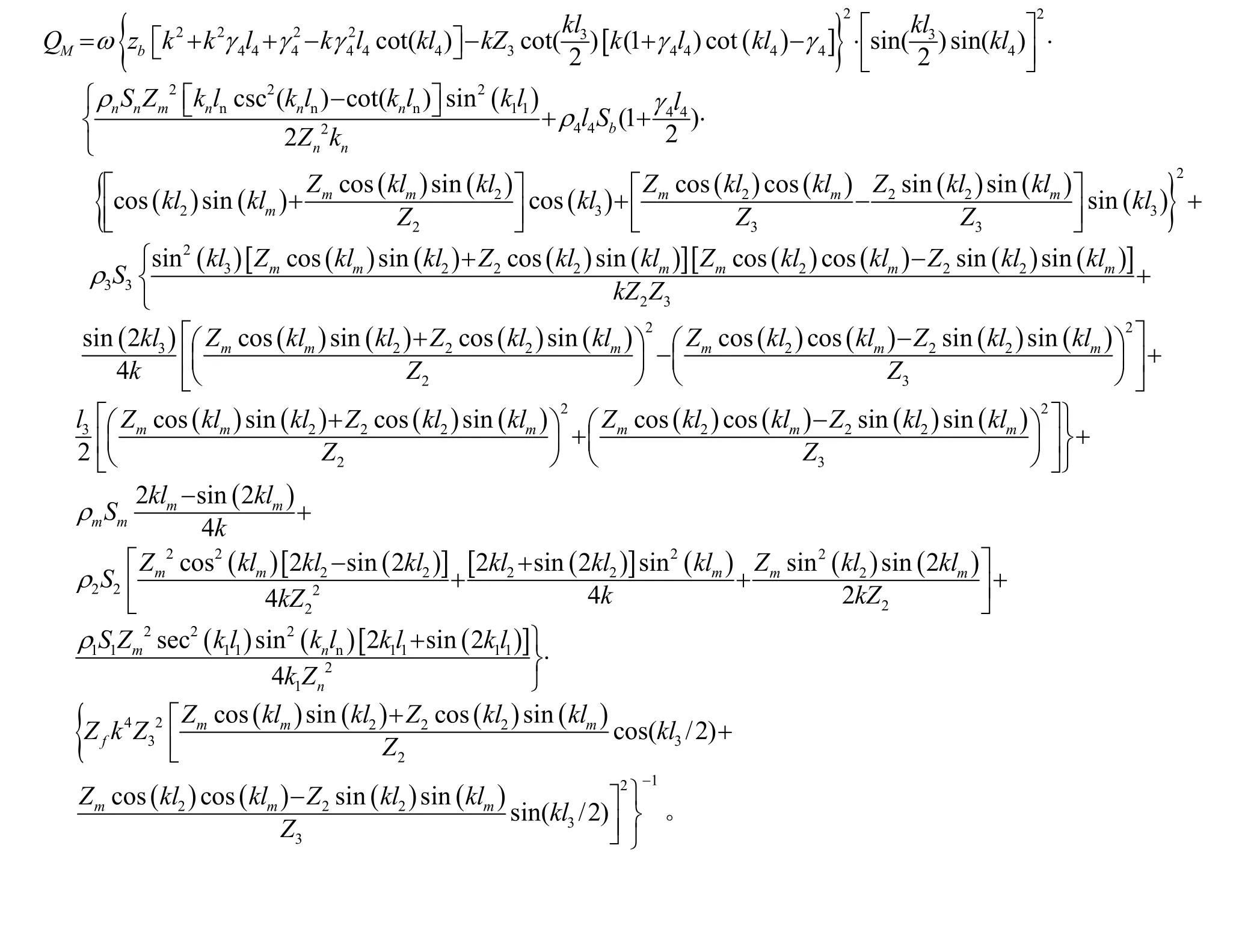基于机械品质因数的全波压电超声换能器设计

胡 涛，刘 宇，傅 波

(四川大学机械工程学院，四川成都610065)

0 引 言

随着科技的进步，制造方法也变得多样化。相比于传统的车铣刨磨等加工方式，超声加工、电火花加工等特种加工方式能够解决传统加工方法难以处理的加工难题，在精密加工领域得到了广泛的应用。作为超声加工的核心，压电超声换能器的优化设计一直是研究的重点内容。目前压电超声换能器的常规设计方法是从四端网络入手[1-4]，利用力电类比的方法，推导出复合变幅杆的等效电路图，结合波动方程[5-8]，进行超声换能器的设计和优化。这些设计方法主要针对半波压电超声换能器，对于全波压电超声换能器，各部分涉及的尺寸参数较多，频率方程存在多值多解的情况，需要比较繁琐的设计优化过程。本文从全波压电超声换能器的机械品质因数出发，预先设定一个符合实际要求的机械品质因数，减少尺寸变量。通过换能器等效点处的等效电路和等效质量推导计算机械品质因数的公式，结合机械品质因数和频率方程的等高线图，更加快捷合理地设计全波压电超声换能器各部分尺寸。

1 全波压电超声换能器的频率方程及等效电路

常见的全波压电超声换能器的结构如图 1所示，后盖板为圆柱形，前盖板由变截面阶梯圆柱及末端锥形工具头组成。其前盖板的长度可按照半波长规律延长，图中虚线部分表示全波长超声振子的振动位移示意图(①、②为节面)。为保证压电超声换能器在工作时能量损失尽可能小，在实际使用时通常在节面位置进行装夹。如图1所示，为保证装夹的可靠性和稳定性且不失一般性，在对该结构的压电超声换能器进行设计分析时，如果第m段的材料为压电材料，此时变幅杆包含两段阶梯，节面处于压电陶瓷晶堆的中部；如果将该段的材料定义为前盖板的材料，则此时前盖板包含三段阶梯，其节面位置位于压电片与前盖板的贴合面处。

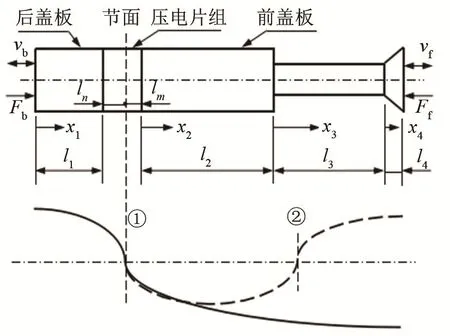
图1 全波压电超声换能器结构及振动位移示意图Fig1 Structure and displacement diagrams of full wave ultrasonic transducer

根据现有的压电基础理论及连续性杆的基本几何方程、物理方程及平衡方程，可以快速得到压电超声换能器圆柱段的波动方程[8]。方程通解的实数部分为

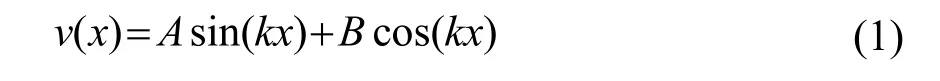
式中：A、B为压电超声换能器圆柱段振速的待定常数；k为波数。当代入各段(后盖板、前盖板、压电晶片)的尺寸参数，利用结合面的速度与力的边界条件即可求得相应的常数 A、B。由振速(其中为振动位移复变量)，声阻抗Z=ρcS，可得到力F的表达式：

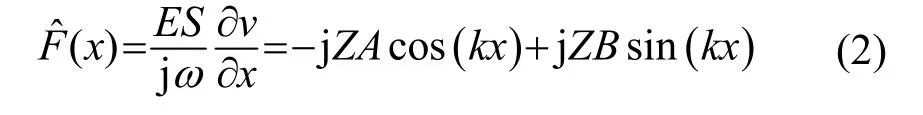
式中：E为弹性模量；S为截面积；ω为振动角频率；c为声速。

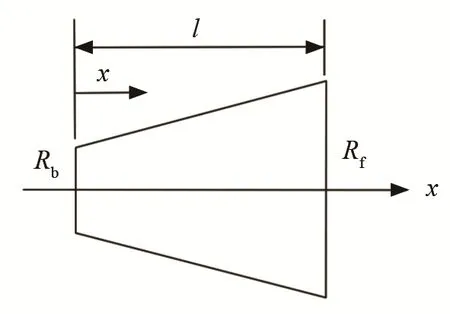
图2 圆锥形变幅杆结构示意图Fig.2 Structural diagram of conical horn

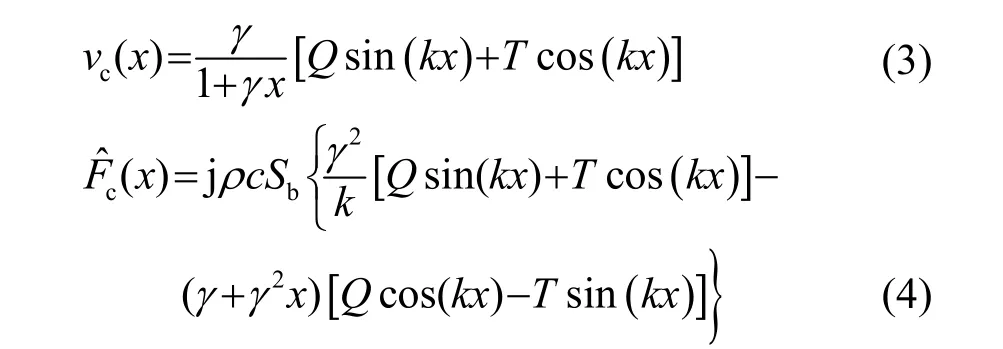
1.1 全波压电超声换能器节面左半部分的振速及频率方程

如图1所示，分析节面左半部分的1/4波长的组件，在理想情况下压电超声换能器各组件贴合面处力F与速度v是连续的，末端一般处于空气中，可认为后盖板的负载阻抗为零；若分别以各振动单元左端点为坐标零点，其边界条件可表示为

由式(5c)及式(2)可得 1/4波长超声振子的频率方程：

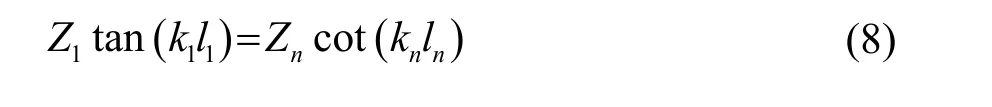
1.2 全波压电超声换能器节面右半部分的振速及频率方程

如前所述，若分别以各振动单元左端点为坐标零点，由压电超声换能器组件之间的贴合面处力F与速度v的连续性可知，各组件之间的边界条件为

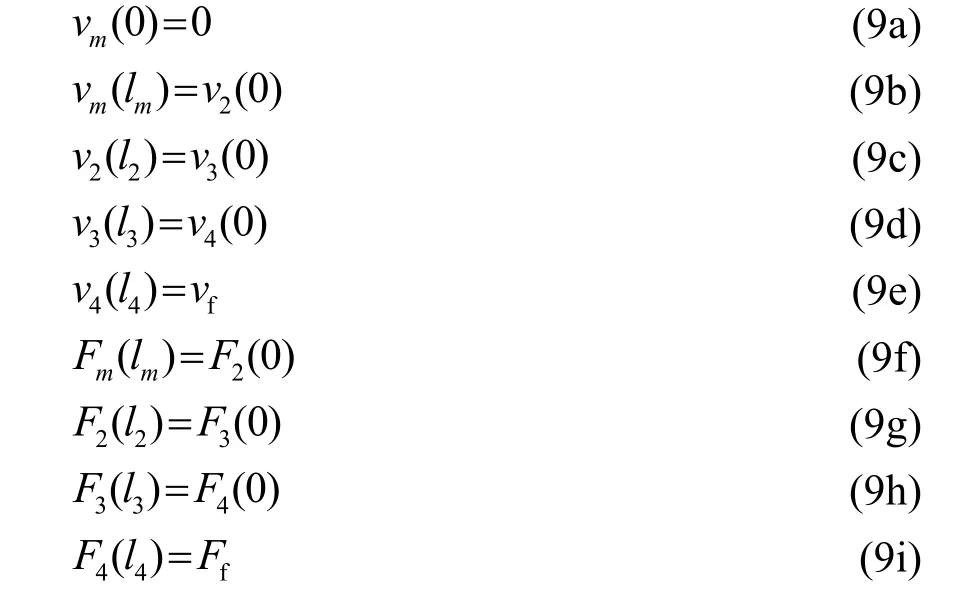
式中：vf为压电超声振子前盖板末端的输出振速，Ff为前盖板末端的输入力阻，在实际应用中Ff的值难以测量或估计，工程设计时通常用压电超声换能器处于空气中的频率方程计算尺寸参数，在后期的优化设计中对其加以调整即可达到使用要求，故此处取 Ff= 0。利用式(9a)～(9h)计算出节面右半部分的各段的振速与力的待定参数，节面右端各段的振速可表示为

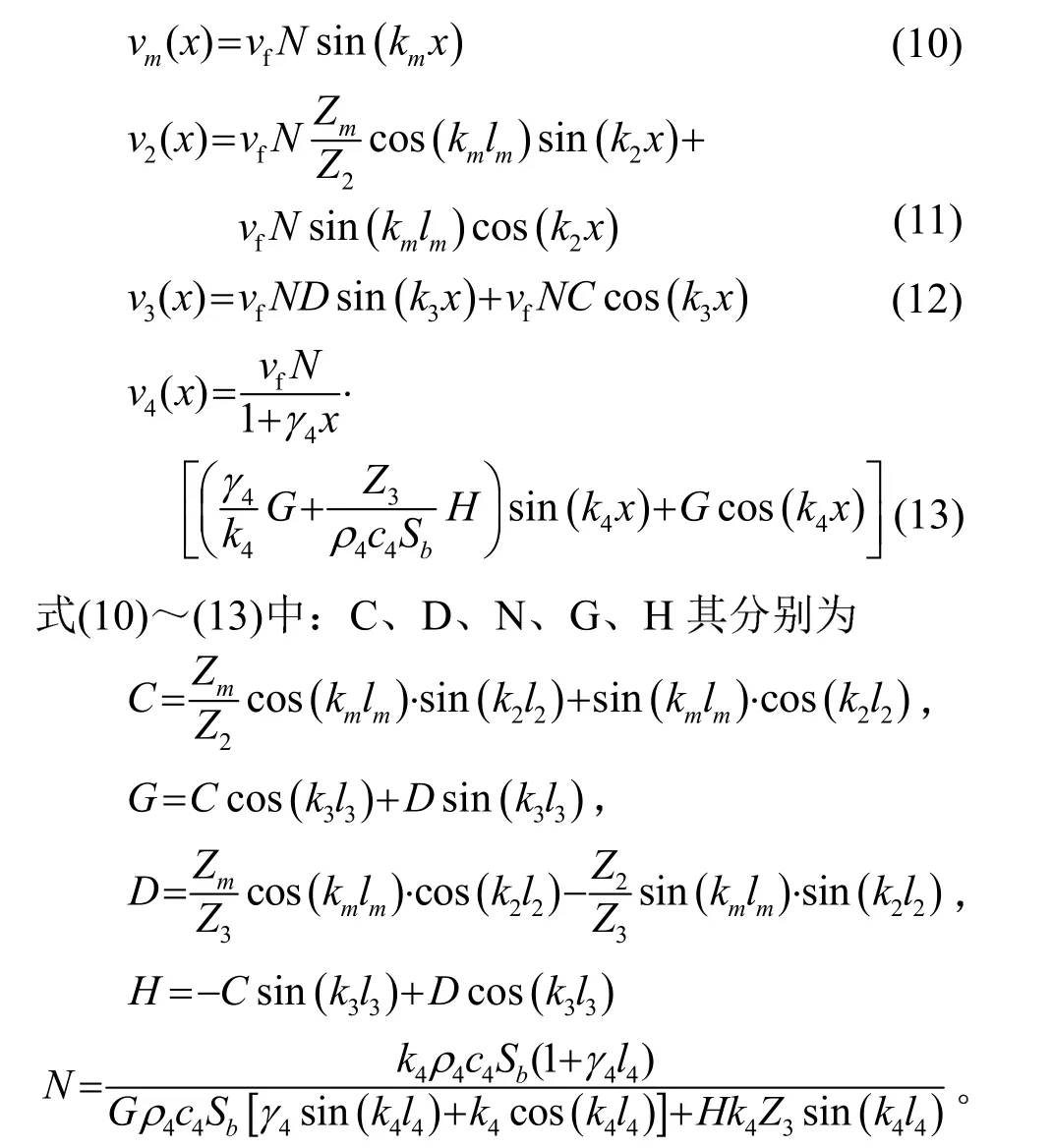
与全波压电超声换能器节面左边的1/4波长振子类似，需要推导出对设计计算有实效的频率方程，将以上各式代入式(9i)，经过运算与化简，可计算出全波超声换能器节面右边部分频率方程：

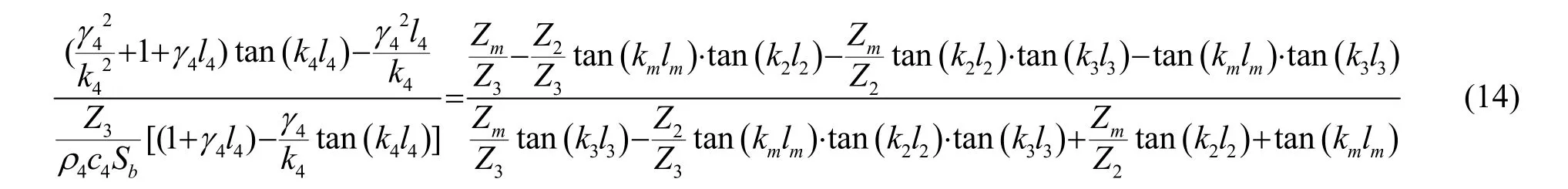
1.3 全波压电超声换能器等效电路及特性参数

1.3.1 前、后盖板圆柱部分的等效电路

前、后盖板的等效电路[9-10]可以很容易由机械杆的串联四端网络推导出。图3为圆柱型杆的四端边界条件，等效电路如图4所示，图中等效参数的具体表达式为

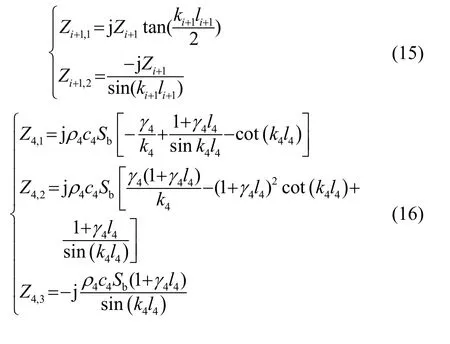
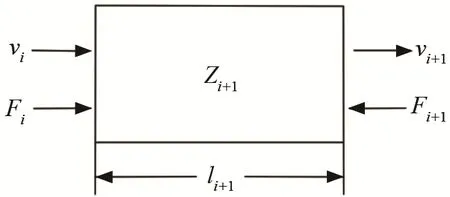
图3 前、后盖板中圆柱部分边界条件示意图Fig.3 Schematic diagram of boundary conditions of cylinder part in front and rear cover plates

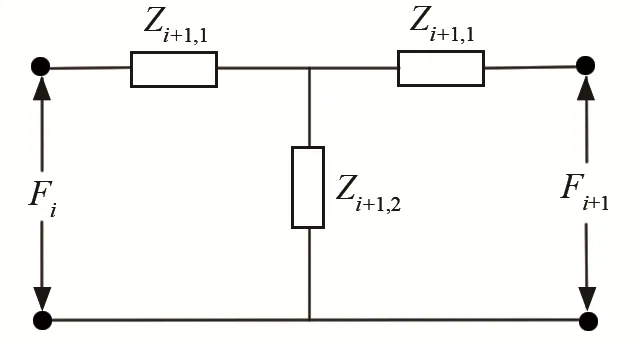
图4 前、后盖板中圆柱部分的等效电路图Fig.4 Equivalent circuit diagram of cylinder part in front and rear cover plates

1.3.2 前盖板圆锥部分的等效电路

前盖板中圆锥部分的机械四端边界条件与圆柱部分相同，如图5所示。等效电路可表示为6所示，相关参数为

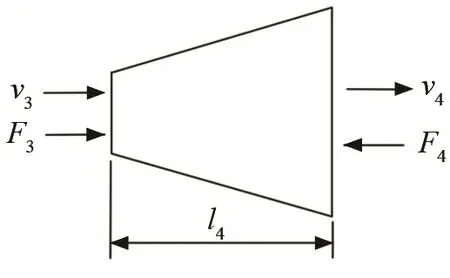
图5 前盖板中圆锥部分边界条件示意图Fig.5 Boundary condition diagram of cone part in front cover plate

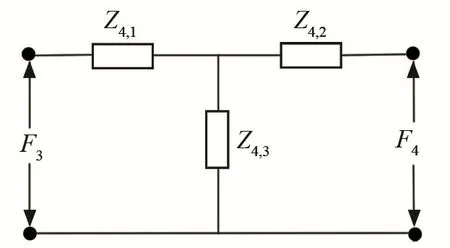
图6 前盖板中圆锥部分的等效电路图Fig.6 Equivalent circuit diagram of cone part in front cover plate

根据本文所分析的全波压电超声换能器结构，可得其等效电路如图7所示。

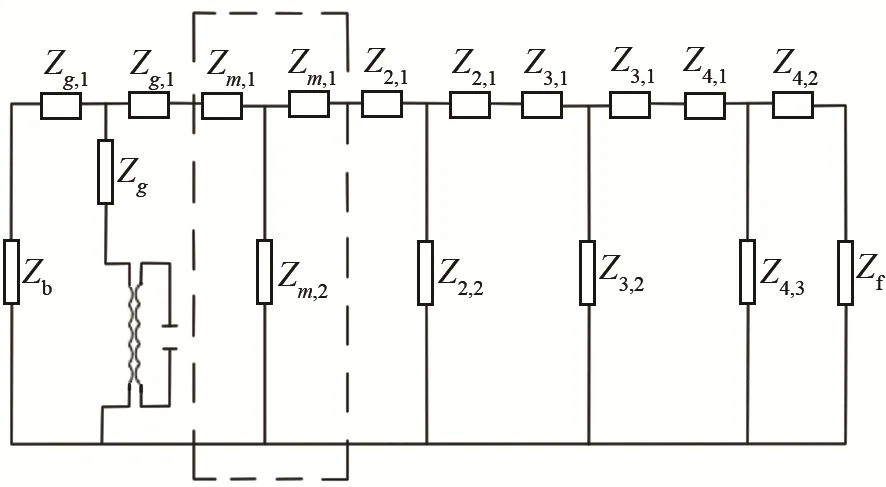
图7 压电超声换能器的等效电路Fig.7 Equivalent circuit of piezoelectric ultrasonic transducer

Zb为压电超声换能器后盖板输入阻抗，Zf为前盖板负载阻抗，当压电超声换能器应用于大功率场合时，其负载阻抗不可忽略。当后盖板处于空气中时，Zb可表示为

2 全波压电超声换能器的机械品质因数

由波动理论可知，当工作频率等于压电换能器的固有基波特征频率时，整个压电换能器即达到谐振状态。如果在谐振频率附近推算压电超声换能器的动态机械阻抗，并将此与同等状态下的LC串联电路比较，在一级近似的条件下，压电换能器的等效质量可以等效为LC串联电路中的电感，压电超声换能器的机械品质因数[10]可表示为

式中：ωs为压电超声换能器谐振状态下的角频率，Me为等效质量，Re为压电超声换能器换算到参考点的等效机械阻。以下利用前面的频率方程和传输矩阵，推导出全波压电超声换能器机械品质因数的具体表达式。

2.1 全波压电超声换能器等效质量的计算

由能量等效原理可知，压电超声换能器在参考点处谐振时的等效质量Me满足如下关系式：

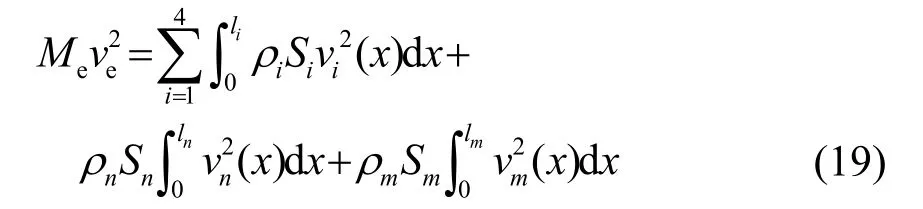
式中：ve为参考点的振速；S为压电超声换能器各组成部分的横截面积。由节面处力的连续性可得力连续方程：

为了保证压电超声换能器在整个振动系统中的振动特性及阻抗匹配，一般，故式(20)可表示为

将式(6)、(7)及式(10)～(13)代入式(19)，并由力的连续方程可得压电超声换能器在参考点处的等效质量：

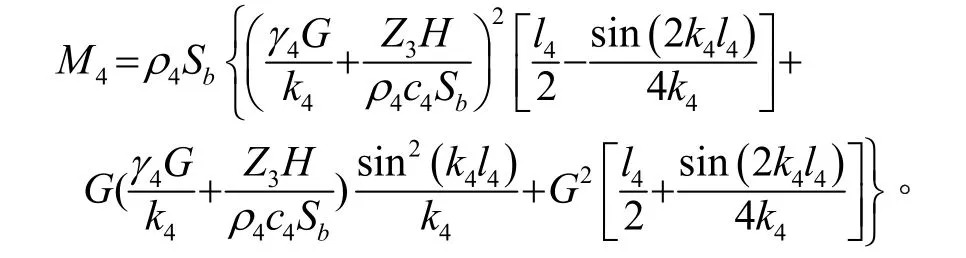
2.2 全波压电超声换能器等效阻抗的计算

压电超声换能器相对应的等效机械阻需要选定在等效质量同一参考点。如图8(a)所示，现考虑前盖板输出端处于空气中的负载阻抗，并根据图 7所示的等效电路图将末端的等效负载阻抗等效到前盖板的所有阶梯变截面处，如图8(b)、8(c)、8(d)、8(e)所示。

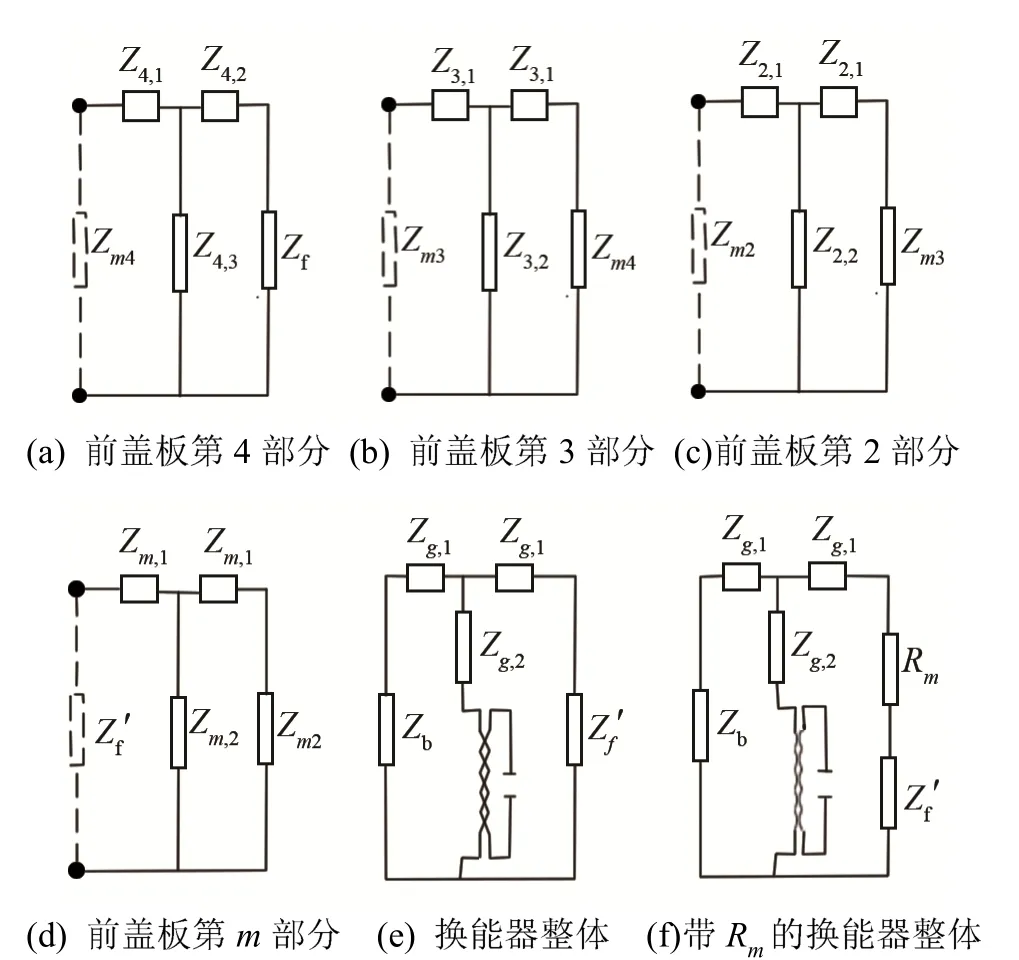
图8 等效阻抗图Fig.8 Equivalent impedance diagram

图8中Zm4、Zm3、Zm2、Zf′分别表示前盖板第4部分、第3部分、第2部分、第m部分等效的输入阻抗(包括负载阻抗与材料特性阻抗的总和)，经过简单的运算，各等效点的等效输入阻抗为

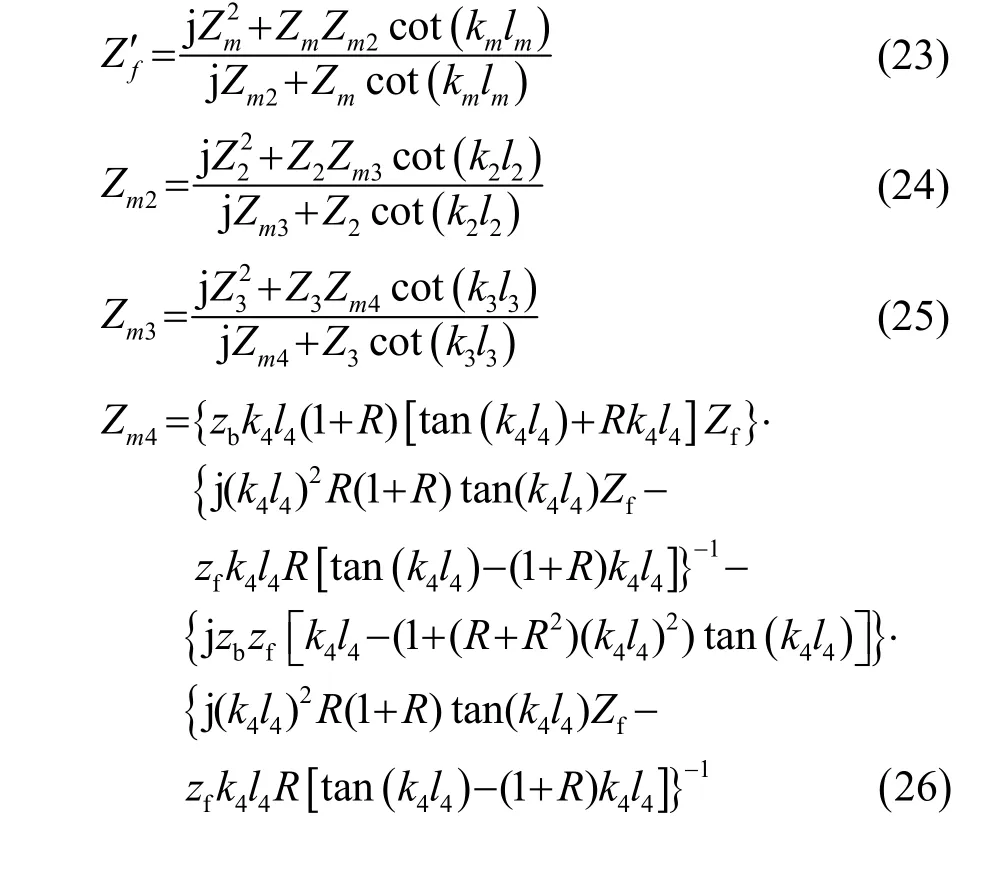
若考虑电能损失和压电超声换能器的结构阻尼，则需在压电陶瓷晶堆端面的等效阻抗上串联一个损耗电阻Rm，如图8(f)所示；同时，压电陶瓷片端面所受的来自前盖板、变幅杆、工具头及负载的总等效输入阻抗可表示为为等效输入电阻，Xf为等效输入电抗。

2.3 等效点的选取

在以往的研究[11]中，为了方便计算，等效点一般选定在压电超声换能器前盖板与压电片贴合面处，本文选定前盖板阶梯变幅杆小圆柱部分中部的振速为参考点振速ve，依据式(12)，第3段中点的参考振速为

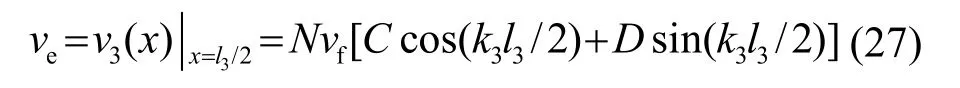
利用电路等效原理将末端的负载阻抗Zf等效到l3的中点处，将式(26)代入式(25)，并对结果进行分母有理化，由于负载阻抗中电阻部分的存在，才会使得在电压作用部分电能转换为热能，所以将表达式的分子中带有虚数单位的项去掉，从而可以得到等效到l3中点处的负载电阻，经过化简有：

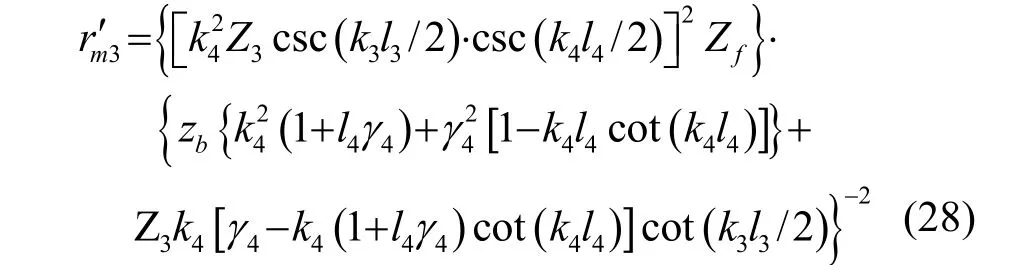
由式(28)可知，当电抗分量的尺寸参数确定后，等效到前盖板第3段中点的等效负载阻抗Zm3与末端的输入负载阻抗Zf成正比，所以在利用超声换能器的机械品质因数QM对其尺寸进行优化设计时可以不用将输入的负载阻抗计算在内，即只考虑压电超声换能器各部分尺寸参数对其机械品质因数的影响即可。

将式(27)、式(28)代入式(18)，可以得到整个全波压电超声换能器的机械品质因数的表达式为

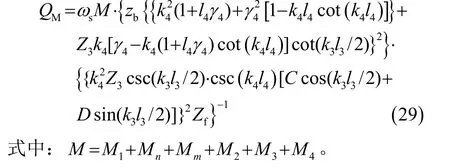
3 基于机械品质因数的全波压电超声换能器设计算例

以应用较广泛的功率为 200 W、谐振频率为28 kHz、结构如图1所示的全波压电超声换能器为例，具体阐述本文所提出的设计方法。考虑一般的应用环境，采用规格为∅20×∅8×6 mm的PZT-8圆环形压电片。

当压电超声换能器的功率、压电片材料及规格确定后，可利用式(30)计算出所需的压电片片数：

式中：n为压电片数量；P为压电超声振子的输入功率；U为压电片的功率容量，通常取 2～3 W·(kHz·cm3)-1；f为压电超声振子的谐振频率。故所需的压电片片数为

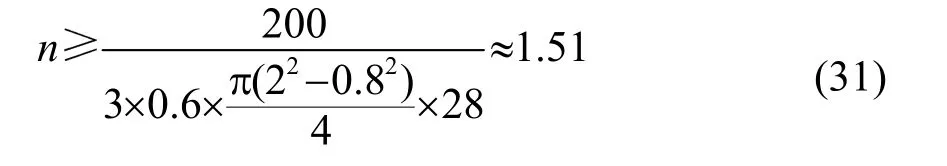
将计算结果取整数，即压电片片数应选择2片。压电超声换能器各组件的材料及属性汇总如表1中所示。

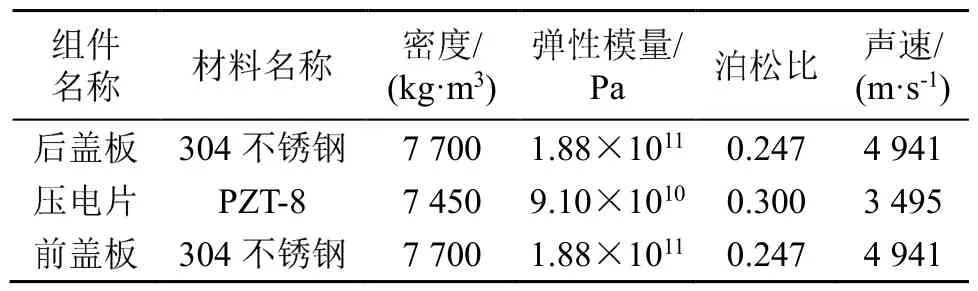
表1 压电超声换能器各组件材料及属性Table 1 Properties of components’ materials of ultrasonic transducer

利用1/4波长超声振子的频率方程(8)对后盖板进行设计计算，式中k1、kn为已知量；为保证在预紧螺栓的预紧力作用下压电片整个端面能被后盖板压紧，一般取后盖板的直径与压电片直径相同，即R1=Rn=1 0 mm，将材料的特征参数值代入式中，即可求得超声振子后盖板的长度。本文中的超声换能器的后盖板模型采用第1阶纵振模态，故所求得的后盖板长度l1=22 mm。由于压电片规格已选定，依前述有：Rn=10mm。

为了简化模型，按照换能器传统结构，将节面设定在压电片与前盖板的接触面处，故在后续的优化设计中，将图1所示结构的m段视为前盖板。由于喇叭状工具头很小，相比于整个压电超声换能器的总等效质量，其占比很少，为了简化计算，可以用工具输入端的振速代替整个工具头的振动速度，同时将喇叭状工具头等效为底面面积与工具头中部横截面面积相等的圆柱体，并利用动量守恒原理可计算出喇叭状工具头的等效质量：

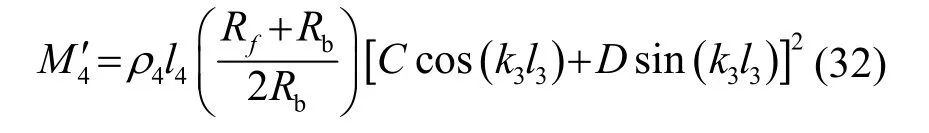
稍加推导即可求得整个压电超声换能器机械品质因数QM的关系式，具体显示表达式详见附录I。算例中全波压电超声换能器的结构较复杂，依据其结构特点及应用场合对其结构做出了适当简化，并事先确定部分尺寸参数，如表2所示。

表2 压电超声换能器各部分已确定尺寸参数Table 2 The size parameters of each part of piezoelectric ultrasonic transducer

从表2中可见：本例中第m段的长度lm、第2段的长度l2与半径r2、第3段的长度l3为未知参数。整个全波压电超声换能器的QM可表示为

由于该关系式比较复杂，甚至很难利用计算机直接进行求解，本文提出了如下的前盖板设计计算方法：为了减少设计时不必要的计算分析，可以在某一特定机械QM值时，利用等高点的方式给定r2、l2的值绘出lm、l3的尺寸变化关系图，与此同时绘制出在该条件下所对应频率方程等于零的等高点曲线，通过比较两等高点曲线，即可确定该特定尺寸r2、l2下是否存在lm、l3的优质解，并可较准确地确定相应的尺寸参数。该方法是一种降维分析方法，回避了解QM方程、频率方程的繁琐过程(由于存在多值多解，有时利用计算机都无法求解)，对于求解此问题是极为有效的。

以r2=5 mm、l2=30 mm为例说明等高点法优化设计的过程，此时压电超声换能器前盖板的频率方程式(14)为lm、l3的函数，前盖板的谐振条件为lm、l3满足该频率方程，故式(14)恒为0，利用此关系可以绘制出该频率方程的等高曲线，同时也可以描述为压电超声换能器在谐振状态下lm、l3的变化关系曲线，如图9所示。理想的前盖板优化设计需使所设计的振子具有较高的机械QM值，由于结构阻尼的存在，整个压电超声振子系统的机械QM值不会高于压电材料的QM值，d33模式PZT压电陶瓷材料机械品质因数的范围一般为 500～1 000[9]，为此，先在式(33)中设定一个较为合理的QM值(可取1 000)，并以此函数绘制该QM值下lm、l3的变化关系曲线，即此状态下的等高曲线，如图10所示。

频率方程反映的是压电超声换能器处于谐振状态下其各振动元件尺寸应满足的关系，由波的传导理论知，谐振振动元件沿其轴向可能有多个振幅为0的点，即相对应多个节面位置，所以频率方程也包含了该关系，图9中所显示的就是一阶纵振、二阶纵振状态下lm、l3应满足的关系。结合图 9、图10可得图11。由图11可知，频率方程等高曲线与品质因数等高曲线若有交点则为优值点，结合QM函数等高曲线中的极值区，若该lm、l3在该点附近区域内取值时，所设计的压电超声换能器机械QM值都将比所选定的值大，则取交点附近一段区域为优值区间，频率方程等高曲线若与品质因数等高曲线没有交点，说明在该特定尺寸r2、l2下，lm与l3取值不能同时满足所需机械品质因数和频率方程，则尽可能取两曲线最为接近的点选取优值区间。优值区间的确定，缩小了Mathematica程序求解频率方程的搜索区间，提高了计算的效率和准确性。

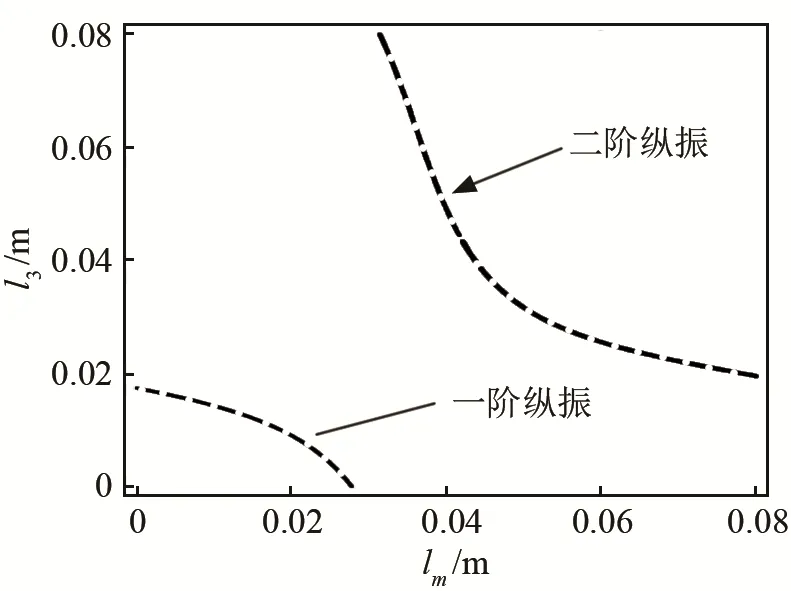
图9 频率方程等高曲线Fig.9 Contour curve of frequency equation

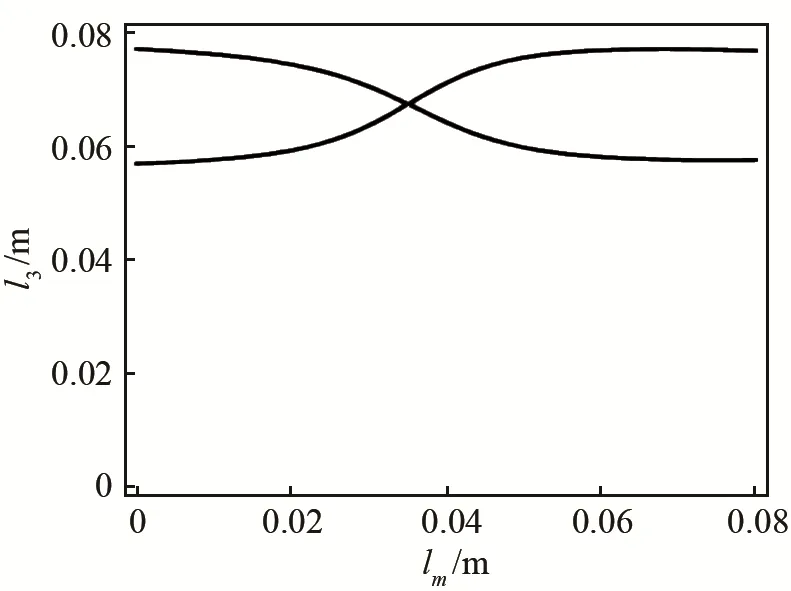
图10 QM函数等高曲线Fig.10 Contour curve of QM function

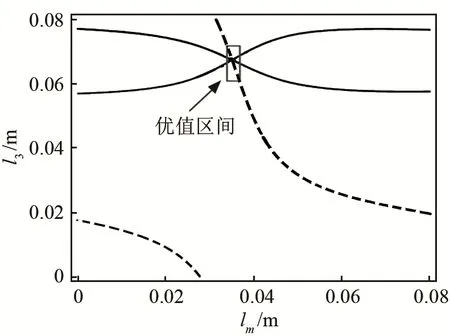
图11 频率方程和QM等高线混合图Fig.11 Mixed graph of frequency equation and QM contour

利用以上方法，求得了几组优质参数值，如表3所示。

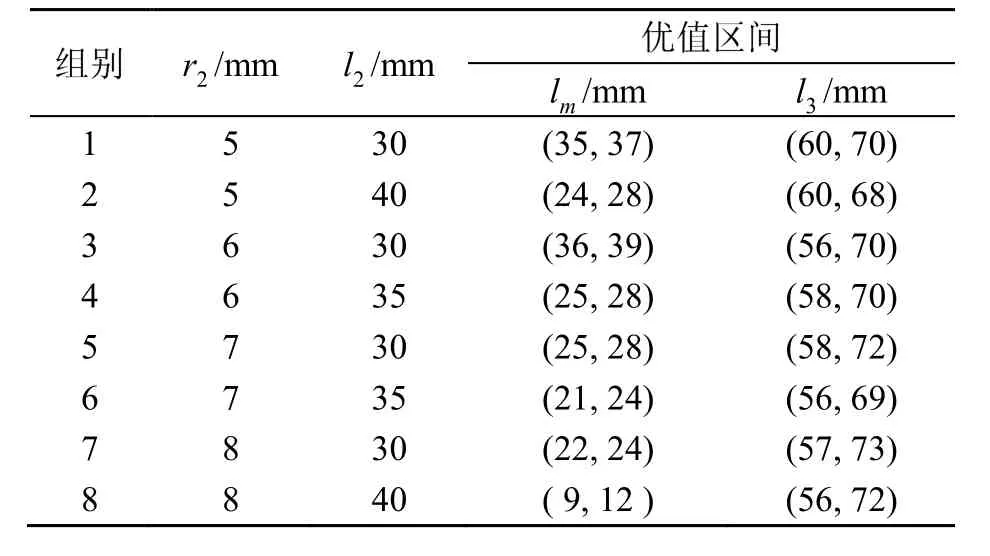
表3 前盖板尺寸的优值区间Table 3 Optimal value range of front cover plate sizes

4 仿真分析

依据表 3，分别选取算例模型前盖板优化后的几组特定r2、l2尺寸以及相应的lm或l3的优值，利用频率方程式(14)分别计算出l3或lm的长度值；利用所得全波压电超声换能器的所有尺寸参数在SolidWorks软件中建立其前盖板、压电片、后盖板的零件模型并将零件进行装配，从而得到整个换能器的装配体模型；将模型导入 ANSYS Workbench软件中进行模态分析，求取特定纵振模态下压电超声振子的特征频率，与设计频率28 kHz对比分析，验证本文所建议的优化设计方法的可行性。

为了使三维建模软件与建立频率方程时的模型具有良好的一致性，压电片、后盖板、前盖板分别采用实心结构。以r2=5 mm、l2=30 mm为例，参照表 3中lm的优值区间，选取lm=36 mm，在Mathematica软件中利用频率方程(14)求解l3的长度，依据实例模型可知此时l3的长度应为64 mm。

依据上述方法选取了8组模型，并分别通过频率方程式(14)计算得到l3的值，将所有模型的尺寸参数列于表4中。

以1号模型振子为例，经ANSYS Workbench软件分析，其振动模态分析结果如图12所示。

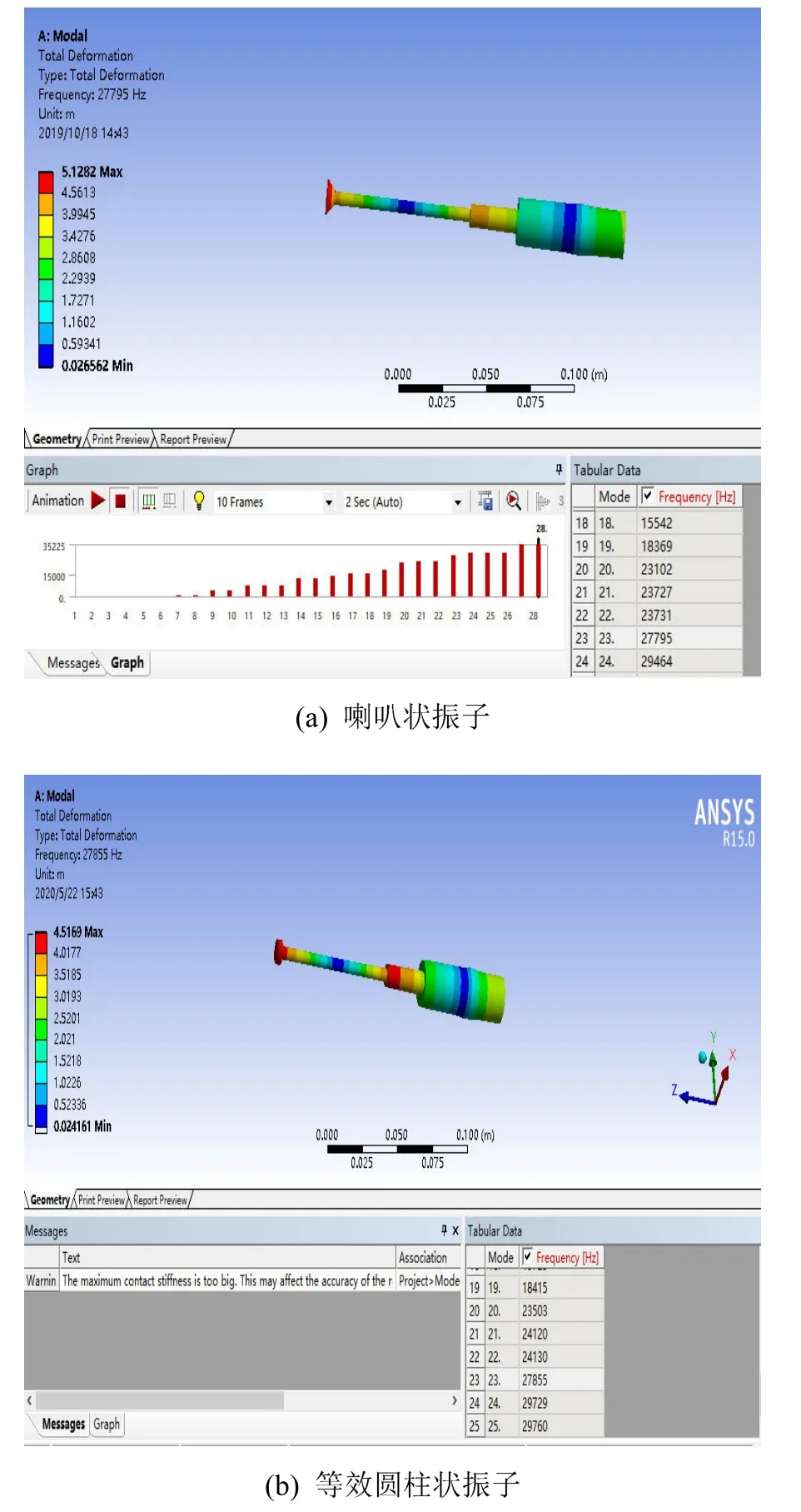
图12 压电超声换能器1号模型纵向模态振动云图Fig.12 Cloud chart of longitudinal mode vibration of Model 1

从分析结果中可见，该压电超声换能器模型在第 23阶模态为纵振模态，节面位置处于压电片与前盖板贴合面位置附近，喇叭状振子谐振频率为27.795 kHz，等效圆柱体工具头振子谐振频率为27.855 kHz，两者误差率为0.2%，符合工程上等效处理要求，且与其设计节面位置和设计频率28 kHz均具有良好的一致性；谐振频率与其前后振动模态的频率相隔较远，具有较大的频带宽，在使用中可以避免其他振动形式的干涉。建立表4中所有对照组的装配体模型，对其进行模态分析并提取其第二阶纵振模态下的谐振频率，结果如表5所示。

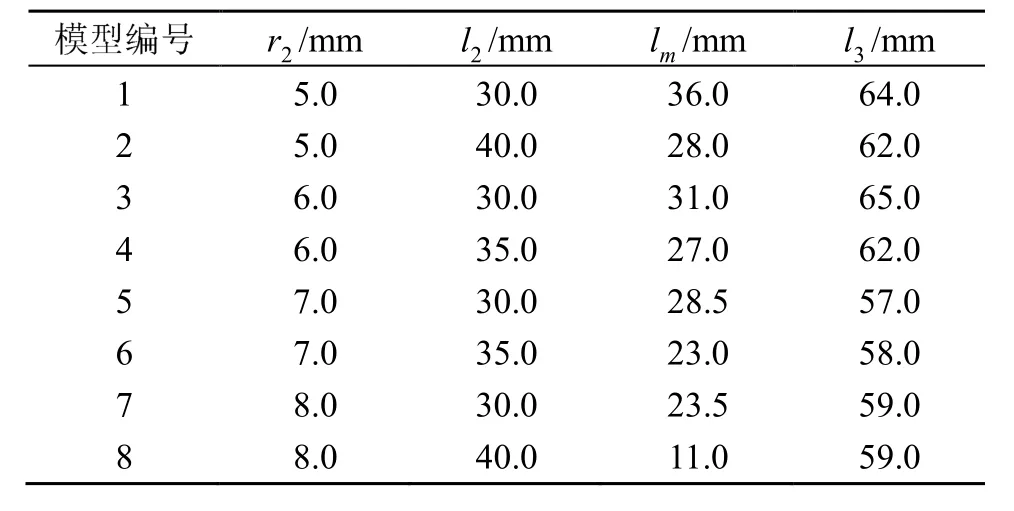
表4 压电超声换能器8组模型的前盖板尺寸参数计算值Table 4 Calculated size parameters of front cover plate for 8 model groups of piezoelectric ultrasonic transducer

由表5中数据可知，利用本文方法计算获得的全波压电超声换能器尺寸，其模型谐振频率的仿真值略低于设计频率。其原因可能为仿真模型在其特征纵振模态处也包含了其附近的振动模态，只是其纵振振动位移占据了其总位移的绝大部分，而在理论推导中并未考虑不同振动方式相互叠加与耦合的情况，只考虑仅存在沿一维杆轴向的振动，导致了软件仿真值与设计值之间存在误差。从8组模型谐振频率的仿真值可以看出，其大小均与设计值28 kHz很接近，最大差值为 500 Hz，最小差值为200 Hz，与实际情况符合良好，设计中对计算出的模型尺寸参数稍加调整(适当减小l3)或直接作为实际模型的尺寸值即可，可以提高该类型压电超声换能器的设计效率。

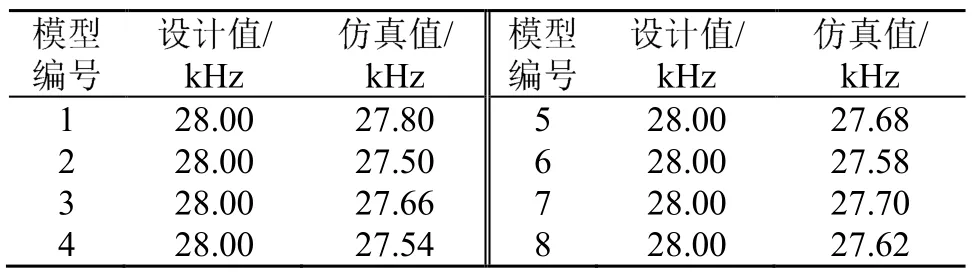
表5 8组模型谐振频率计算值与仿真值对照表Table 5 Comparison table of calculated and simulated resonance frequencies for the 8 model groups

在压电超声换能器的设计过程中，也可以直接固定节面位置在压电片与前盖板接触处，简化设计参数，将前盖板三段阶梯杆变为两段更易满足设计要求，也可以引入阶梯段的放大系数作为新的参考量，对阶梯段的各段尺寸进行限制。

5 结 论

本文针对全波压电超声换能器结构复杂，其频率方程存在多值多解的情况，提出了一种基于机械品质因数关系式的全波压电超声换能器结构优化设计方法，在压电超声换能器的频率方程和等效电路图的基础上，推导出与其各个组件尺寸参数相关的压电超声换能器机械品质因数的表达式，结合图解法、等高点法得到模型结构尺寸参数的优值区间，进而利用Mathematica程序求解频率方程得到压电超声换能器的结构尺寸。利用有限元软件ANSYS对该尺寸的全波压电超声换能器进行了模态分析，仿真分析得到的谐振频率与设计频率的误差很小，验证了本文所建议的全波压电超声换能器结构设计方法的合理性，为全波压电超声换能器结构优化设计方法的研究提供参考。

附录I

压电超声振子的机械品质因数的计算公式：