拟牛顿优化BP网络盲判决反馈均衡器
王 凯,吴立新
(1. 中国科学院声学研究所,北京100190;2. 中国科学院大学,北京100049)
0 引 言
无需训练序列的盲均衡技术对于多径效应严重且带宽有限的水声信道来说是十分重要的,可以有效降低码间干扰对通信系统的影响,提升系统的通信性能。均衡器根据对接收信号的处理方式不同可以划分为线性均衡器和非线性均衡器。线性均衡器结构和算法简单,适用于信道畸变不严重的情况,当均衡器阶数足够长时,可以达到理想的均衡效果;而在水声通信系统中,信道往往存在频率选择性衰落,非线性均衡器能够有效地消除水声信道的符号间干扰。
神经网络均衡器属于非线性均衡器,由于其优秀的非线性拟合能力,受到了国内外科研工作者的关注,文献[1]首次将多层感知器(Multi-Layer Perceptron, MLP)应用于信道均衡,该方法采用四层多层感知器结构,证明了多层感知器均衡器可以克服信道非线性和加性噪声的干扰,文献[2]对误差反向传播(Back Propagation, BP)网络均衡器进行改进,加入了函数连接结构,均衡效果优于最小均方算法,文献[3]将契比雪夫(Chebyshev)多项式与BP网络结合,在二进制信号均衡中取得了较好的效果,文献[4-5]分别将遗传算法与粒子滤波算法与BP网络结合,在收敛速度、误码率方面均有所改进。已有的基于BP网络的均衡器主要针对网络结构选取与优化方面进行研究,仅用神经网络结构完成均衡,没有与常规均衡方法相结合的算法。本文提出一种将神经网络与判决反馈均衡器结合的盲均衡器结构,用单隐层BP网络判决反馈均衡器(Decision Feedback Equalization, DFE)的前馈滤波器和反馈滤波器。
传统的神经网络都是基于梯度下降法进行迭代计算的,存在收敛速度慢的问题,影响均衡性能。牛顿法通过利用目标函数的Hession矩阵进行迭代计算,具有二次收敛性,收敛速度较快,但是需要计算二阶导数,计算复杂度较高,且当Hessian矩阵非正定时可能出现发散的情况。拟牛顿法通过构造正定对称的近似矩阵来进行迭代计算,解决了牛顿法存在的问题。因此本文采用拟牛顿方法进行神经网络的权值迭代,利用一个近似矩阵来近似Hessian矩阵的逆矩阵,通过网络权值梯度的变化量进行逐层的迭代计算,兼顾了拟牛顿的收敛速度以及神经网络的非线性拟合能力。对四相相移键控(Quadrature Phase Shift Keying, QPSK)调制信号的均衡仿真验证了本文方法在消除码间干扰,降低误码率,加快收敛速度方面相比于传统方法的优越性。
1 复数BP网络
BP神经网络是一种多层前馈神经网络,工作过程主要包含两部分:信号的正向传播和误差的反向传播。文献[6]已经证明:用单隐层的前馈神经网络能够以任意精度逼近任意的连续函数。图1为均衡器网络结构,其中输入神经元的个数为M,隐含层神经元的个数为 I,m = 1 ,2… M ,i=1 ,2,… I 分别为输入层到隐含层、隐含层到输出层的连接权值,本文采用QPSK信号进行仿真,因此输入、输出及权值皆为复数。
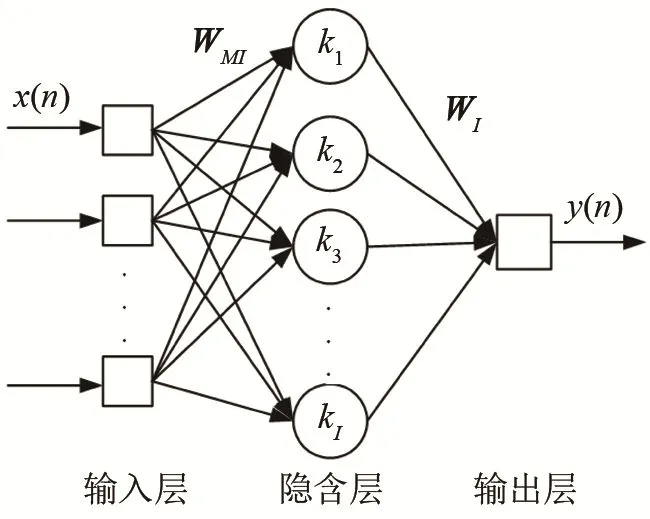
图1 单隐层BP网络示意图Fig.1 Schematic diagram of single Hidden Layer BP Network
令vM(n)= x ( n)表示输入层的输出,uI(n)表示隐含层的输入,vI(n)表示隐含层的输出,y( n)表示输出层的输出,f(⋅)表示激活函数,*代表取复共轭转置,则有:

实数神经网络的激活函数需要满足输入区间内单调、有界及非线性等条件,常用的有 tansig、logsig、Relu等函数。复数神经网络激活函数与实数情况下要求有所不同。根据文献[7]激活函数f( x + i y) = u ( x, y) + i v( x, y)应满足以下要求:
(1)f( x+iy)在x和y上非线性,保证为网络引入非线性变换,否则神经网络的性能会受到影响;
根据以上条件,选择激活函数为

其中:r和c为正实数。
2 BP网络盲判决反馈均衡器
基于BP网络的盲判决反馈均衡器分为两个阶段:学习阶段和收敛阶段。学习阶段将反馈滤波器置于前馈滤波器之前,先对数据进行白化处理,再用横模盲均衡(Constant Modulus Algorithm, CMA)算法对数据进行均衡,当反馈项具有一定可信度时转换到收敛阶段,此时均衡器结构为常规的 DFE均衡器,使用反馈项作为期望信号对信号进行均衡。
2.1 学习阶段
学习阶段均衡器结构设置如图 2,依次为增益控制因子g—反馈项BP网络R—前馈项BP网络T相位修正因子e−jθ—判决器。其中增益控制因子用来缩小接收信号的动态范围,便于输入到神经网络进行处理;反馈项BP网络R、前馈项BP网络T分别完成常规DFE前馈和反馈滤波器的功能;相位修正因子e−jθ用来修正信道和接收端处理对数据造成的相位偏移。根据文献[8]可知,R的输出是DFE的反馈输入,在无训练序列的情况下只有当R的输出具有一定可信度时才能作为反馈项输入。因此,学习阶段首先将R置于T之前,对R的参数进行学习。

图2 学习阶段均衡器级联框图Fig.2 Equalizer cascade diagram in learning stage

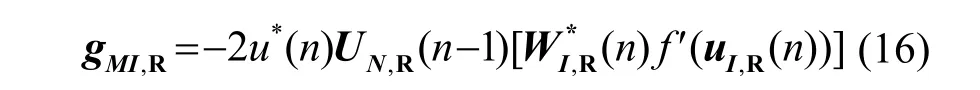
对于网络T,在无监督学习情况下对恒定包络的信号依据Godard盲均衡算法有:
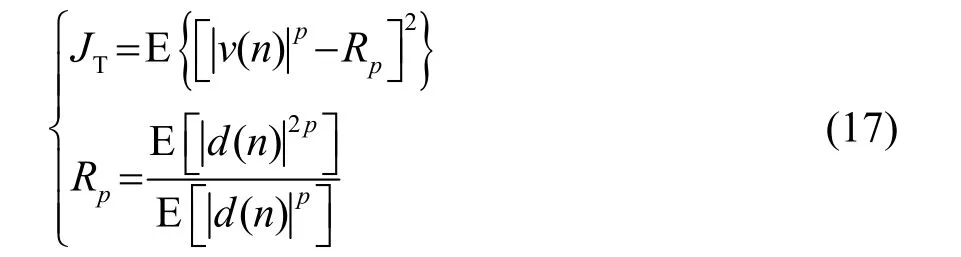
其中:p代表对输出信号特性统计的阶数,当 p=2时,此算法成为最常用的恒模盲均衡算法(CMA),令,可得:

文献[10]已经证明,在初始模式级联方式下,应用Godard算法时,当且仅当T达到迫零准则时均衡器取得最优值,相比于 MSE准则仅有细微的差别。

由代价函数可知,计算Jθ时需要用到此时刻的判决值,因此需要将e−jθ放置在最后。根据文献[11],用二阶锁相环最小化Jθ的方法为

2.1.3 拟牛顿BP网络迭代
拟牛顿迭代方法与最速下降法一样只要求知道目标函数的梯度,通过对梯度变化的测量,构造一个目标函数的模型使其满足超线性收敛,其性能要优于最速下降法。另外,因为不需要二阶导数信息,所以其相对于牛顿法计算量更小,而且可以保证矩阵的正定,防止牛顿法可能出现的收敛发散的情况。
拟牛顿法主要思想为对目标函数进行二阶泰勒展开并令其导数等于0,推导得出权值迭代公式。对J(ω)在ω(n)处进行二阶泰勒展开:
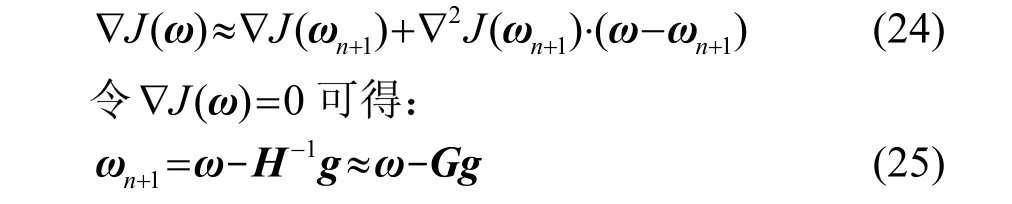
其中: H−1表示二阶导数Hession矩阵的逆矩阵,G表示它的近似值,g表示梯度矩阵。
由BFGS迭代法可得近似矩阵G的迭代公式:
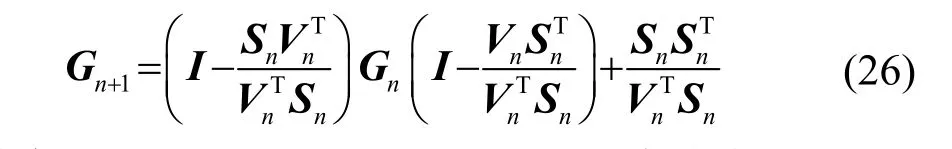
由2.1.2节已经得到了R、T两个网络各层权值的梯度计算公式,根据上述公式可以得到拟牛顿BP网络权值迭代步骤如下:
(5) 根据式(25)计算GI、GMI;
(7) 输入新数据重复步骤(1)~(6)。
2.2 收敛阶段
当初始模式的判决输出具有一定可信度时,均衡器级联结构由图2转变为图3。此时均衡器为加入相位修正的常规DFE结构,将判决输出的结果当作期望信号进行训练。当模式转化时,均衡器受到的影响仅为T由近似迫零准则转化为MSE准则对网络权值的影响,对整个均衡器影响较小。同时新的均衡级联结构相比于初始模式可以达到更小的均方误差。

图3 收敛阶段均衡器级联框图Fig.3 Equalizer cascade diagram in convergence stage
由于均衡器没有训练序列,不能直接根据误码率评价初始模式下判决信号的可靠性,而均方差可以根据调制方式转化为误码率,因此我们将判决信号与输出信号的均方差值作为度量初始模式均衡效果的性能指标。度量值M由以下公式计算:
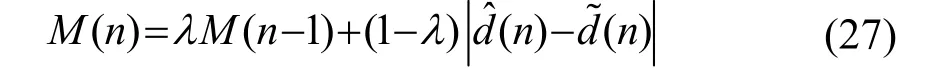
其中:λ为遗忘因子,一般取接近1、但小于1的常数,保证均衡器不会在初始阶段与收敛阶段来回震荡,模式切换准则为

为了保证模式转换后的判决信号具有可靠性,M0的选择应该足够小。通常选择当误符号率小于0.02时进行模式转换,相移键控(Phase Shift Keying,PSK)调制符号错误概率与信噪比关系为

根据Wirtinger计算方法,两BP网络的各层权值梯度可表示为

由 2.1.3节的网络权值迭代步骤对网络权值进行迭代。
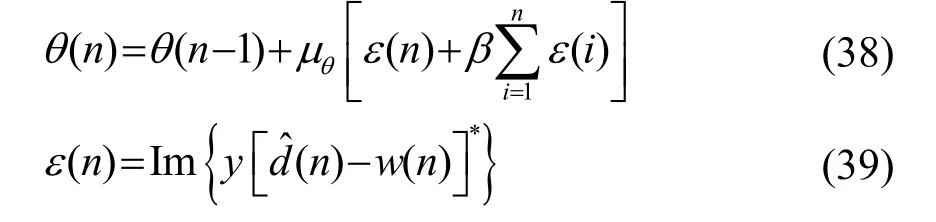
3 数值仿真
本文仿真对比了 QPSK调制下,拟牛顿优化BP网络盲判决反馈均衡器(Blind-Quasi Newton Optimization BP Network Decision Feedback Equalizer, B-QNBPDFE)、BP网络盲判决反馈均衡器(Blind-BP Network Decision Feedback Equalizer,B-BPDFE)以及常规盲判决反馈均衡器(Blind-Decision Feedback Equalizer, B-DFE)三种均衡器在衰落信道中的均衡效果。其中两个神经网络均衡器反馈项和前馈项分别有20、5个抽头输入,隐层神经元个数分别为4和2,B-DFE反馈和前馈抽头个数均分别为 20、5。仿真采用具有混合相位复数信道[12],信道冲击响应为

同时为其增加一个二次的非线性变换y=x + 0 .2x2和时变相位偏移φ( n )= πn Δ +θ0,其中 Δ的取值范围为0~10-3,θ0代表0~2π的初始相移。
图4(a)为该信道的零点,4(b)、4(c)为幅频响应曲线。可以看出该信道具有明显的频率选择性衰落和严重的相位失真,且单位圆内和单位圆外均有零点分布,是典型的混合相位信道。


图4 仿真信道的特性Fig.4 The characteristics of the simulation channel
如图 5(a)、5(b)分别为本文方法(B-QNBPDFE)和B-DFE均衡后的星座图,5(c)为信噪比15 dB下,100次蒙特卡洛仿真结果。可以看出,本文方法相较于B-DFE,两种神经网络均衡器收敛时有更低的均方误差,均衡后星座图更加收敛。同时本文方法与 B-BPDFE相比具有更快的收敛速度,且均方误差更小。
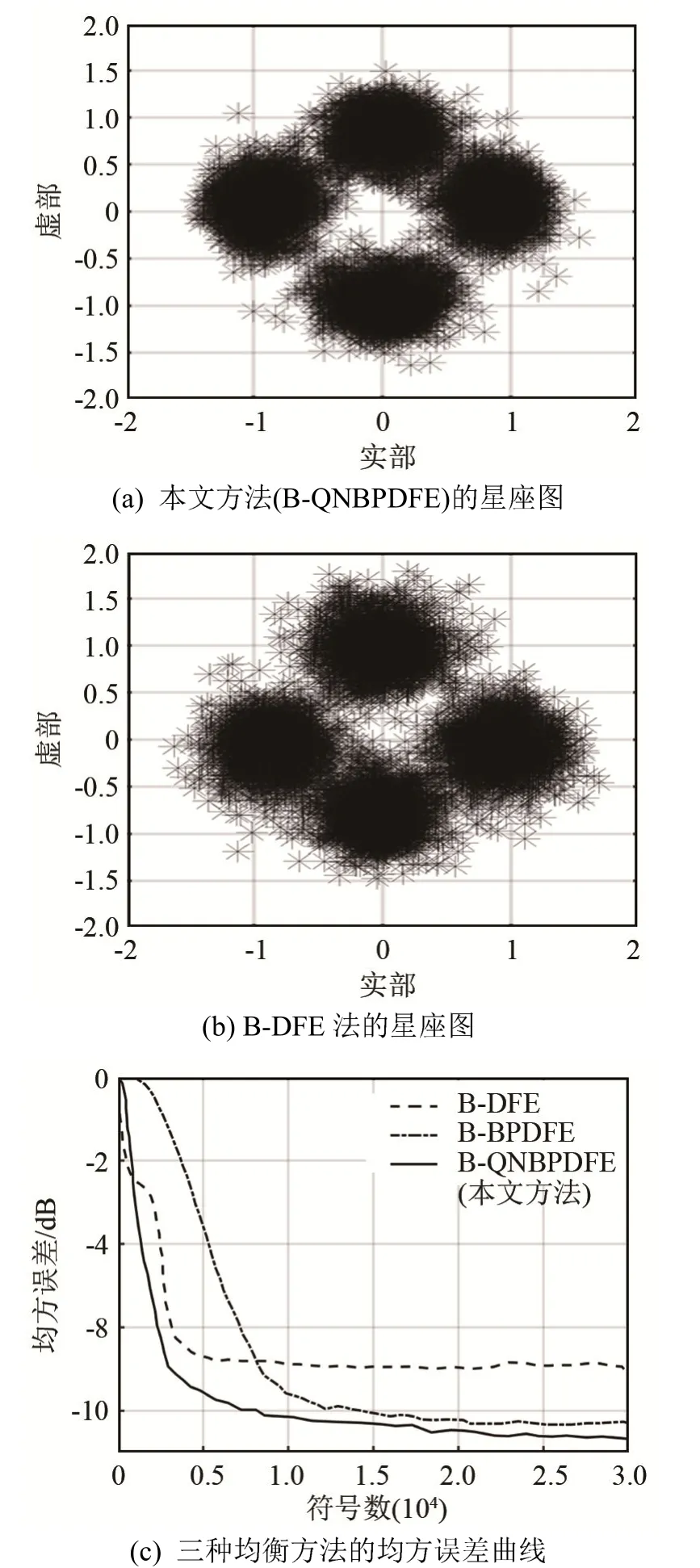
图5 信噪比为15 dB时,三种均衡方法的信道均衡效果的比较Fig.5 Comparison of the equalization effects of three different equalization methods in the channel when signal to noise ratio is 15 dB
图6为不同信噪比情况下三种均衡器误码率变化曲线。从图 6中可以看出,本文方法与 B-DFE相比有更低的误码率。
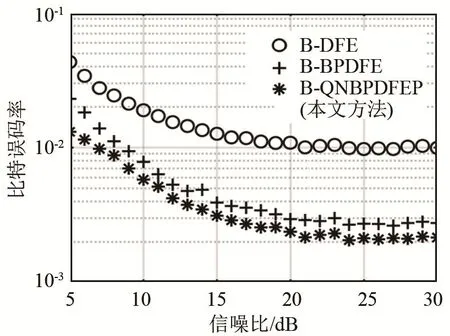
图6 不同信噪比下三种均衡方法的误码率对比图Fig.2 Bit error rates of three different equalization methods under different signal to noise ratios
4 结 论
本文基于盲判决反馈均衡器的模型,在利用神经网络良好的非线性拟合能力的同时,改进梯度下降法带来的收敛速度慢的问题,提出了拟牛顿优化BP网络的盲判决反馈均衡器。通过利用两个复数BP网络分别实现盲判决反馈均衡中数据白化及常模盲均衡部分,利用拟牛顿迭代进行网络权值的更新,通过改变均衡器级联结构实现对信道的学习与跟踪。仿真结果表明,与盲判决反馈均衡算法相比,本文算法具有更低的均方误差,同时相比梯度下降法收敛速度更快。然而,由于拟牛顿算法不是全局最优算法,虽然能提升均衡器收敛速度,但是依然存在陷入局部极小值的问题,计算复杂度低且全局最优的迭代算法还有待进一步研究。

