一种新型复合局域共振型声子晶体带隙特性
陈琪琪,张 波,白玉田,王立恒
(宁夏大学机械工程学院,宁夏银川750021)
0 引 言
低噪声与良好抗振性是现代装备发展的一个重要目标和特征,过强的噪声振动会严重影响装备的工作性能、效率以及运行的安全性、可靠性和服役寿命等指标。在航空航天领域中,各种武器装备所面临的振动噪声问题更为突出,武器装备系统元件众多、振动耦合形式复杂,同时,传统的减振降噪技术受空间、质量等条件的限制,有一定的局限性,因此发展新的噪声控制理论与降噪技术成为迫切需要。
20世纪90年代,对声子晶体的研究在学术界引起了广泛的关注。声子晶体是由两种或者两种以上介质构成、弹性常数或密度周期性变化的结构。经过特殊设计的声子晶体结构存在能够抑制弹性波传播的频率范围,即带隙。通过改变声子晶体的结构以及材料参数,可以实现人为调控带隙的位置、宽度以及对弹性波的抑制能力[1],这也为拓展传统减振降噪理论和技术提供了新思路和新途径。最初对于声子晶体的研究主要集中在Bragg散射型声子晶体。2000年,武汉大学刘正猷教授首次提出了声子晶体产生带隙的另一种机理——局域共振机理[2],其学术成果为声学材料设计开拓了新的研究领域,也为后续声学超材料的提出提供了思路。局域共振机理是由局域共振单元的谐振特性决定的,对声子晶体结构的周期性不敏感,散射体随机排列也会产生带隙[3]。局域共振型声子晶体的出现改变了人们对只有大尺寸结构才有低频带隙效果的认识。因此,研究局域共振型声子晶体具有重要的研究价值与意义。2006年,国防科技大学 Zhao等[4]将阻尼引入局域共振结构,发现了低频水声反常吸声效应。此后,Wen[5]和Jiang等[6]学者对声子晶体低频吸声机理进行深入研究,提出了基于Mie散射的波形转化效应和多重散射效应的共同作用是低频吸声显著增强的内在机制,在此基础上,又从吸声模态、阻抗匹配的角度对吸声影响因素以及规律进行了系统分析。张思文等[7]以及梁孝东等[8]分别都对局域共振复合单元的声子晶体进行研究,表明在低频范围内能打开多条带隙,这进一步说明复合结构的设计对于打开低频带隙提供了一种有效的方法。在实际应用中,人们需要对声子晶体的带隙机理进行研究,以及深入认识影响带隙的各种因素和规律,以此针对所需的带隙设计声子晶体。
本文在传统局域共振型声子晶体设计基础上,借鉴复合结构[9-10]提出了一种设计思路。即对该结构在原有的局域共振型声子晶体的基础上新增加了一层散射体和一层包覆层,从而使声子晶体具有多重谐振的特点,因此使得结构模态振型更加丰富,具有更好的带隙特性。本文通过建立声子晶体等效模型计算结构带隙的上下边界频率,再对比有限元方法计算得到的带隙,分析其共振带隙的产生机理,最后再分析不同因素对于带隙起止频率的影响。
1 复合局域共振型声子晶体设计
1.1 复合局域共振型声子晶体单元结构设计
图1为本文建立的复合谐振声子晶体元胞结构与周期结构平面图。该声子晶体为局域共振型声子晶体,其中的局域共振单元是由 A(四方柱状散射体)、B(包覆层)、C(层状散射体)、D(基体)组成,即柱状散射体外包裹一层硅橡胶包覆层,再将其嵌入层状散射体中,然后在层状散射体外再包裹一层硅橡胶包覆层,之后将其嵌入环氧树脂基体中,同时内外散射体的面积是相同的,其结构参数见表1。

表1 声子晶体单元的结构参数Table 1 Structure parameters of phononic crystal cell
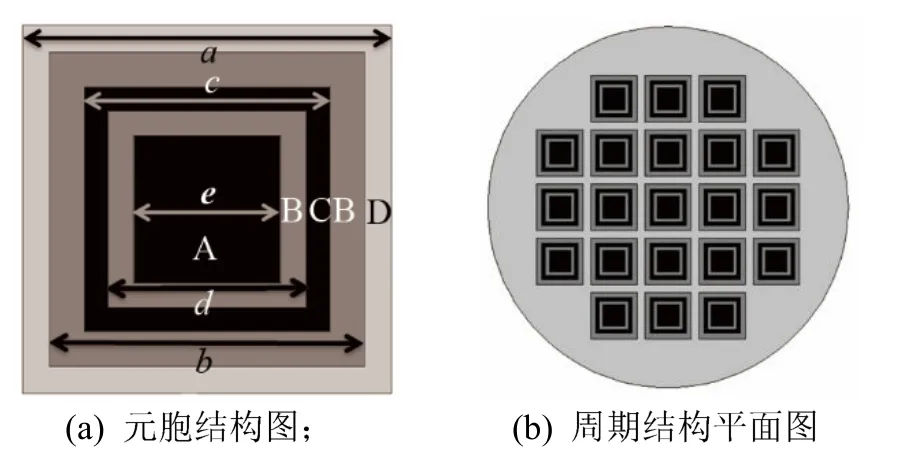
图1 复合谐振声子晶体元胞结构及周期结构平面图Fig.1 The cell structure of multi-harmonic phononic crystal and its plane diagram
单元结构确定后,可采用有限元方法计算该声子晶体模型的带隙。根据Bloch定理与能带理论[11],利用 COMSOL Multiphysics软件设置声子晶体材料,材料相关参数见表2,同时分别在基体框的x、y方向上设置一个Floquet周期边界条件,然后求解元胞在周期边界条件下的特征频率从而得到带隙。根据Bloch定理,对于任意给定的Bloch波数矢量(简称波矢)k,其取值范围限定在不可约 Brillouin区,使k沿着不可约Brillouin的边界M-Γ-X-M上取值,得到本征频率随波矢变化的色散关系曲线,即表示声子晶体带隙的能带结构图。
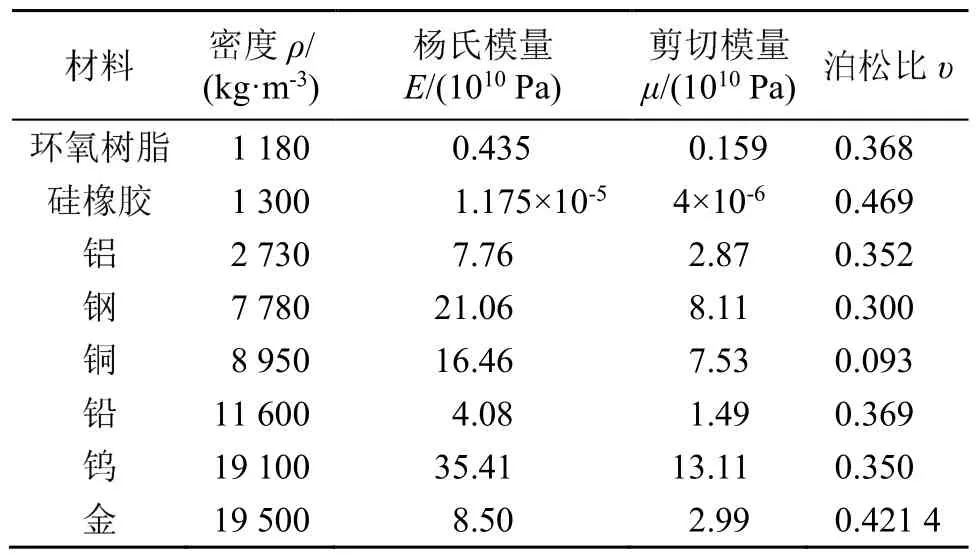
表2 声子晶体单元的材料参数Table 2 Material parameters of phononic crystal cell
1.2 复合局域共振型声子晶体等效模型及带隙特性计算
将局域共振系统简化成弹簧-质量块系统,如图 2所示的周期局域共振弹簧-质量块系统被视为一种声子晶体的基础物理模型,图2(a)中的虚线框内系统代表该周期系统的单个元胞,通过模型进行研究。m1和m2是单个局域振子中的内、外层散射体的等效质量,m3是单元结构基体的等效质量。在带隙的起始频率处,质量块m1和m2与弹簧k1组成一个二自由度系统以不同的频率进行共振;在带隙的截止频率处,考虑在质量块m1和m2的基础上加入基体质量块m3以及弹簧k2,可形成一个三自由度系统,实现共振。
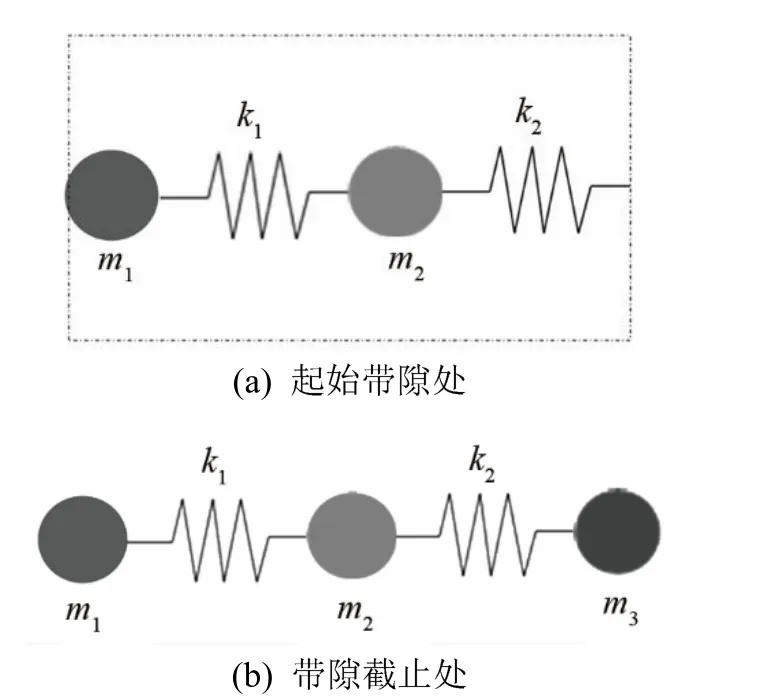
图2 起始带隙处和带隙截止处弹簧-质量系统等效模型Fig.2 Equivalent model of spring-mass system at initial gap and cut-off gap
图3为声子晶体结构质量划分,具体而言,在单个周期的局域共振系统中,设内层散射体的质量是mA1,外层散射体的质量是mA2,基体质量是mt。内层散射体(铝)、包覆层(硅橡胶)、外层散射体(铝)、基体(环氧树脂)的密度分别是ρ1、ρ2、ρ3、ρ4。
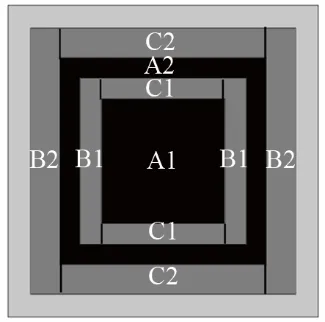
图3 声子晶体结构质量划分图Fig.3 Mass division diagram of phononic crystal structure

根据图3可进一步计算包覆层的等效质量。图3中包覆层B1随着外层散射体一起振动,因此部分质量mB1要计算在外层散射体质量m2中,包覆层B2随着基体一起振动,mB2要计算在基体质量m3中。作为弹簧作用的包覆层C1和C2,需要按照相应的比例分配质量给基体框和散射体。
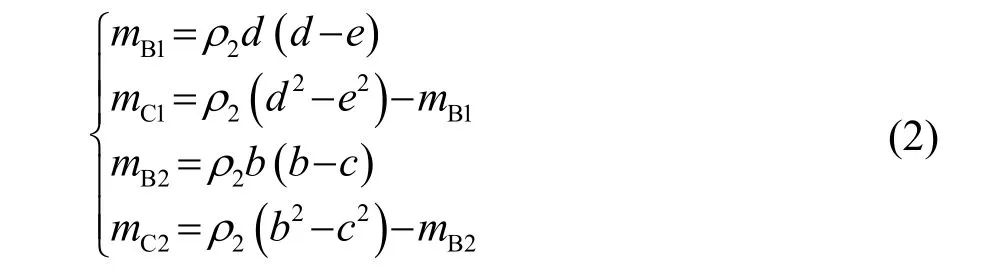
得到等效质量块的质量为
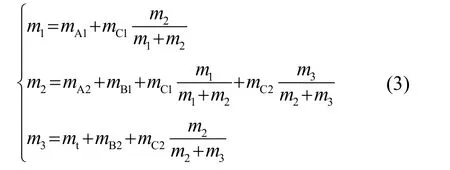
考虑到弹簧的等效刚度仅与包覆层 C1和 C2有关,因此有:
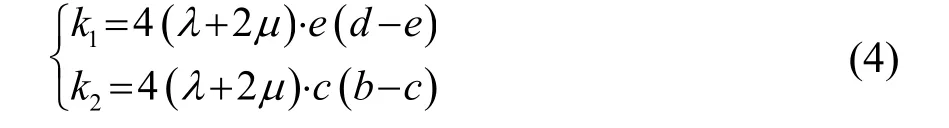
式中:λ和µ分别是硅橡胶包覆层的两个拉梅常数。
在带隙的起始频率处,计算出的刚度矩阵和质量矩阵分别是:
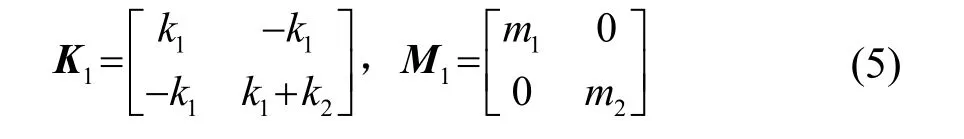
将式(3)、(4)的解代入式(5)得:

其对应的特征值方程为

求解特征方程(6),可得特征值解ω11= 8 13.6 Hz,ω12=1974.95 Hz,其中,ω11,ω12分别为声子晶体带隙的起始频率。
同理,带隙的截止频率处,计算出的刚度矩阵和质量矩阵分别是:
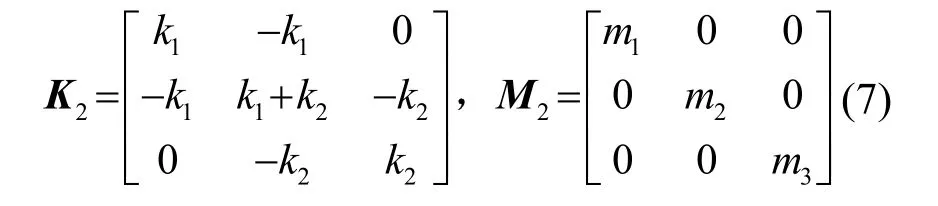
将式(3)、(4)的解代入式(7)得:

其对应的特征值方程为

最后,求解方程(8),可得特征值解ω21= 1 396.03 Hz ,ω22= 2 105.52 Hz ,其中,ω21,ω22分别为声子晶体带隙的截止频率。
1.3 基于有限元法(COMSOL)带隙结构计算
在周期结构声子晶体中,根据Bloch周期条件,可将整体的计算缩减到一系列的单元中进行。因此只选取一个元胞进行分析,在软件中取元胞x和y方向的两条边作为显式,在目的端表达式设置kx和ky,这样就完成了周期边界的设置。在求解器参数中设置所求频率阶数,因为结构规则、应力分布均匀且单元尺寸较小,因此采用常规单元进行有限元网格划分完成求解,如图4所示。在COMSOL软件中,给定一个k值,即可求得一组结构本征频率,最后进行波矢参数扫描,因为研究的声子晶体是正方晶格,所以扫描的边界应该沿着整个Brillouin区边界,Brillouin边界图如图 5所示,当波矢沿着M-Γ-X-M的边界完成参数扫描后,生成的数据即可用以绘制能带结构图。

图4 COMSOL带隙结构计算中的网格划分Fig.4 Mesh division in COMSOL bandgap structure calculation

图5 第一Brillouin区图形和正晶格、倒晶格基矢高对称点坐标Fig.5 Diagram of the first Brillouin region and the coordinates of the height symmetric points of the orthotropic and reciprocal lattice basis vectors
2 共振带隙机理及特性分析
2.1 带隙特性
利用等效模型计算出的带隙频率为 813.6~1 396.03 Hz、1 974.95~2 105.52 Hz。采用COMSOL Multiphysics进行有限元分析时,散射体材料采用金属铝,包覆层采用硅橡胶,基体采用环氧树脂,图 6 为计算出的能带结构图(图6中横坐标 k 0~1为Γ-X边界的水平扫描,1~2为X-M边界的垂直扫描,2~3为M-Γ边界的对角线扫描),从图中可以看出在2 200 Hz左右的频率下有三条明显的带隙,第一条带隙的频率范围是876.23~1 282.4 Hz,对应带宽是 406.17 Hz;第二条带隙的频率范围是 1 284.5~1 396.6 Hz,对应带宽是112.1 Hz,其中第一、二条带隙中间仅有一条水平的通带,通带带宽是2.1 Hz;第三条带隙的频率范围是 1 999.8~2 141.9 Hz,相应带宽是142.1 Hz,第二、第三条带隙之间的通带带宽为 603.2 Hz,因此通带占全部带隙范围的45.71%。由图6可知,两种计算结果基本吻合。
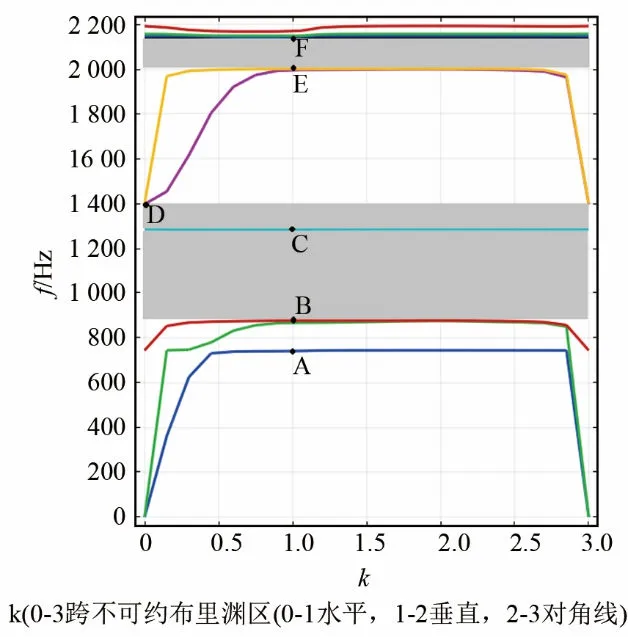
图6 声子晶体能带结构图Fig.6 Structure diagram of phononic crystal bands
由于声子晶体元胞结构具有对称性,因此元胞
在横向与纵向这两种振动模式下具有相同的动力学特性,质量块和弹簧(包覆层)发生振动时,基体外框基本是静止状态。这时的基体外框对于弹簧-质量块这一振动模式来说可以看作是刚性基础,使它被单元结构所局域化,形成了一个局域振子。当这个局域振子受到基体外框所带来的振动时,会产生谐振且与基体外框产生力的作用,同时局域振子会与基体外框中产生的行波长波相互耦合产生带隙。带隙产生的原因是由局域共振系统里面的谐振效应所致,带隙范围内的频率对应局域共振系统的固有频率,当激发的频率与共振单元固有频率相近时,单元结构会产生共振模式,局域共振单元与基体中传播的低频行波强烈耦合,能量传播到共振单元后被局域化,不能继续传播。在图6中,表现从 0点(Γ点)开始的行波能带被共振平直带截断,因此形成了共振带隙,由此可见,禁带边沿的平直带对应的振动模式是局域化共振模式。
为了分析具体带隙产生的原因,本文选取了能带结构图中带隙开始频率以及截至频率处的各点振动模态进行分析(如图7所示),图中箭头代表位移场,箭头方向和长度是代表起点处介质运动的方向和位移大小。
从图7(a)中的A点处的振动模态可以看出,内层散射体带动着内层包覆层一同朝着相同的方向旋转,影响着外层散射体跟随着一起做扭转运动,从受力大小和位移来看,内层散射体先开始的振动,它们一起对外层散射体的影响仅仅使其受到扭转剪切变形,因此导致外层散射体只能对基体产生扭矩作用,从而使作用在基体上的x或y方向上的合力趋于0,基体中的低频行波和散射体的局域共振模式之间的耦合作用较弱,因此对局域共振带隙的产生没有影响。


图7 带隙起始、截止频率处各点的振动模态Fig.7 Vibration modes at different points of band-gap starting and cut-off frequencies
图6中B点和E点都处于带隙的起始位置,对于B点,内层散射体起主导作用进行平移运动,对内层包覆层产生拉伸或压缩运动,而在E点处,外层包覆层起主导作用进行平移运动,对外层散射体产生拉伸或压缩运动,进而使得内层包覆层要发生平移运动,在这两点处的局域振子谐振下,会在 x或y方向上产生合力,基体外框的行波长波与局域振子产生耦合作用,每个相邻的元胞之间的局域振子也是做相反的平移运动,由此产生了带隙。
此外,从图6可知,C点位于一条平直带上,由于内、外散射体和包覆层组成的共振单元呈扭转共振状态,加之这条平直带位于带隙中,因此形成一条窄通带。
D点与B点为同一带隙的截止频率点与起始频率点的振动模式,它们是相互对应的,因此放在一起分析。在D点处内层散射体与外层散射体和基体朝着相反的方向移动,使得作用在基体上的x或y方向上产生的合力慢慢减小,该局域振子与基体外框的行波长波产生的耦合作用逐渐减弱,导致带隙截止。同理,F点与E点也是相对应的同一条带隙的截止、起始频率点处的振动模式,此时F点处内层散射体基本保持不动,外层散射体与基体朝着相反的方向移动,在x或y方向上产生的合力慢慢减小,与基体外框的行波长波产生的耦合作用减弱,导致带隙截止。
根据上述对单元结构共振模态的分析可以发现,声子晶体的带隙是局域振子谐振与基体中的行波长波发生耦合作用的结果,这个耦合作用是否存在,是决定带隙产生的关键因素。
2.2 传输特性
通过能带结构来分析和计算声子晶体禁带时,通常考虑的是无限周期理想声子晶体。但实际工程中的结构往往为有限周期,这就使能带结构中带隙频率范围内某些弹性波的能量衰减不彻底而仍然能透过有限声学结构。因此,对于有限结构声子晶体,需要能够反映有限结构弹性波传输特性的指标和参数。本文采用传输特性定义激励与响应之间的关系,即幅频响应关系。频率响应函数反映了结构对激励的传递能力,它以频率为自变量,将激励和响应的时间历程通过 Fourier变换转换为各个频率下的幅值比,就得到了传输谱LdB,定义如下:

式中:X是输出端或响应端的物理量;X0是入射端或激励端的物理量。根据带隙特性,有限周期结构声子晶体的幅频响应函数会在带隙频率范围内的对应区域有明显的降低,这个降低幅度反映了弹性波的衰减程度。
为便于和实验测试结果对比,本文进一步采用COMSOL Multiphysics软件计算声子晶体传输特性曲线。计算时采用 3×3个有限周期结构(如图 8所示),计算模型采用固体力学模块,为了得到较为准确的传输谱计算结果,防止激励端反射波和输出端散射波的影响,使用完美匹配边界(Pefect Matching Layer, PML)来吸收多余的干扰波,这个外加区域不会产生任何反射。在传输谱的计算中,上、下周期边界条件的设计以及材料结构的设置与带隙特性计算设置相同。计算时,在输入端加入激励,然后对输出端进行响应积分,最后通过求响应与激励的比值得到传输谱。

图8 采用COMSOL计算传输特性的声子晶体有限周期结构示意图Fig.8 Limited periodic structure diagram of phononic crystal for transmission characteristics calculation by COMSOL
图9为计算出的传输特性曲线,图中灰色区域表示有明显的衰减,这部分即为带隙范围:830.21~1 473.5 Hz和1 677.81~2 058.6 Hz。与图6的能带结构图相比,对应位置区域基本一致。
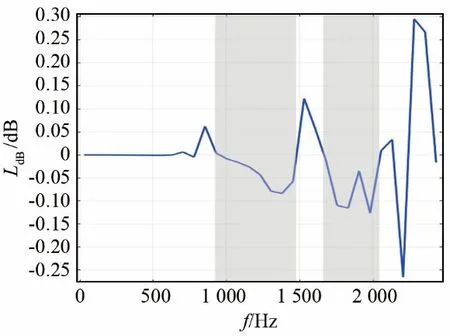
图9 声子晶体传输谱Fig.9 Transmission spectrum of phononic crystal
3 实验测试
为了确定分析设计的声子晶体的带隙范围以及特性的准确性,需要进一步通过实验测试进行验证。因此,本文进一步对声子晶体进行了传递损失测试,采用基于四传感器的隔声量测量系统[12]进行测试,来对比理论及仿真计算出的带隙频率范围是否与测试结果对应。
3.1 声子晶体试件制备
在实验中,复合局域共振声子晶体板的制备方案采用的是先将切割好的铝柱块以及铝柱层分别用硅橡胶包覆层包裹,最后将其按四方周期排列方式排入模具中,在其中填充环氧树脂,固化后制备出声子晶体试件。原材料包括边长为6 mm的正方形铝柱、边长为10 mm厚度为1 mm的正方空心铝柱、厚度分别为1 mm和1.4 mm的硅胶垫以及环氧树脂AB胶。其工艺流程如图10所示。

图10 复合谐振局域共振声子晶体的制备流程Fig.10 Fabrication process of compound resonant local resonant phonon crystal
声子晶体试件厚度为10 mm,如图11所示。采用阻抗管测量结构的隔声效果,根据测试要求,试件直径为 100 mm,其他结构参数与仿真预设值相同(见表1)。

图11 声子晶体试件图Fig.11 Phononic crystal specimen
3.2 测试过程与结果分析
本文采用北京声望 SW422阻抗管隔声测试系统对声子晶体试件进行传递损失测试,该测试管有效测量范围是63~1 600 Hz,因为测试件直径略小于阻抗管直径,因此试样测试前需要在试件外圈包裹几层聚氯乙烯生料带进行密封处理。由于聚氯乙烯生料带具有一定的弹性可以压紧细小缝隙,同时由于它是薄膜材料,当密封点内外有压差时会像气球一样鼓起填补缝隙以增加密封性。实验测试现场如图12所示。


图12 隔声测试现场图Fig.12 Field diagram of sound insulation test
图13为传递损失测试曲线,从图中可以看出复合局域共振型声子晶体结构隔声量在 846~1 518 Hz频段处有三个明显高于其他频段的波峰,最高峰值达到 48 dB。该声子晶体薄板在该频段范围内对噪声的隔声量明显增加,最大隔声量达到48 dB,说明声波在结构内部的传播受到了阻碍,声子晶体禁带对声波传播起到了抑制作用,即该频段范围内具有带隙。
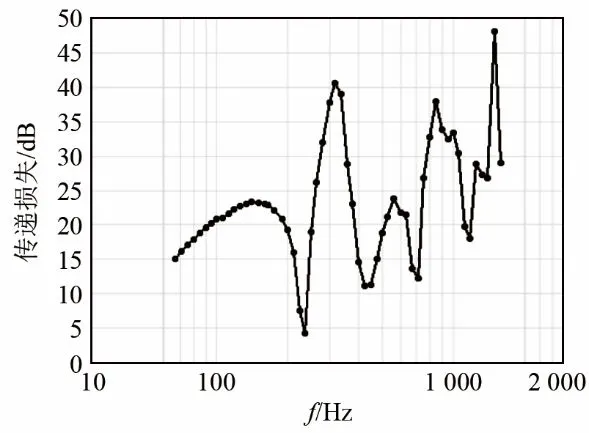
图13 传递损失曲线Fig.13 Transmission loss curve
3.3 实验测试误差分析
(1) 由于试件采用人工方式制备,样品试件中存在着少量气泡,造成了声散射与热黏效应,从而引起理论计算与测试结果之间存在差异。
(2) 受测量仪器限制,制备试件必须为圆形结构,而计算采用的声子晶体模型为四方晶格排列,从而导致局域振子的填充率减小,基体面增大,因而对声子晶体带隙特性产生了影响。导致测试结果与理论结果之间存在差异。
(3) 相比阻抗管内径尺寸,试件尺寸偏小,在阻抗管中试件采取了边界固定的方式,这一边界条件可能会导致声波传播特性改变,对于试件的实验测试结果产生一定的影响。
虽然理论计算与测试结果之间存在一定偏差,但是隔声效果好的测试频段范围与理论计算带隙频段范围基本对应。证明了本文理论分析工作的正确性。
4 带隙影响因素分析
根据前面的等效模型可以看出,带隙主要受两方面因素的影响: 等效质量因素和结构形状因素,具体分析如下。
4.1 散射体密度对带隙的影响
首先是改变材料参数。当采用不同密度材料作为散射体时,散射体密度对带隙的影响如图 14所示,不改变其他材料几何参数,只改变散射体密度时,其影响分以下两种情况讨论:
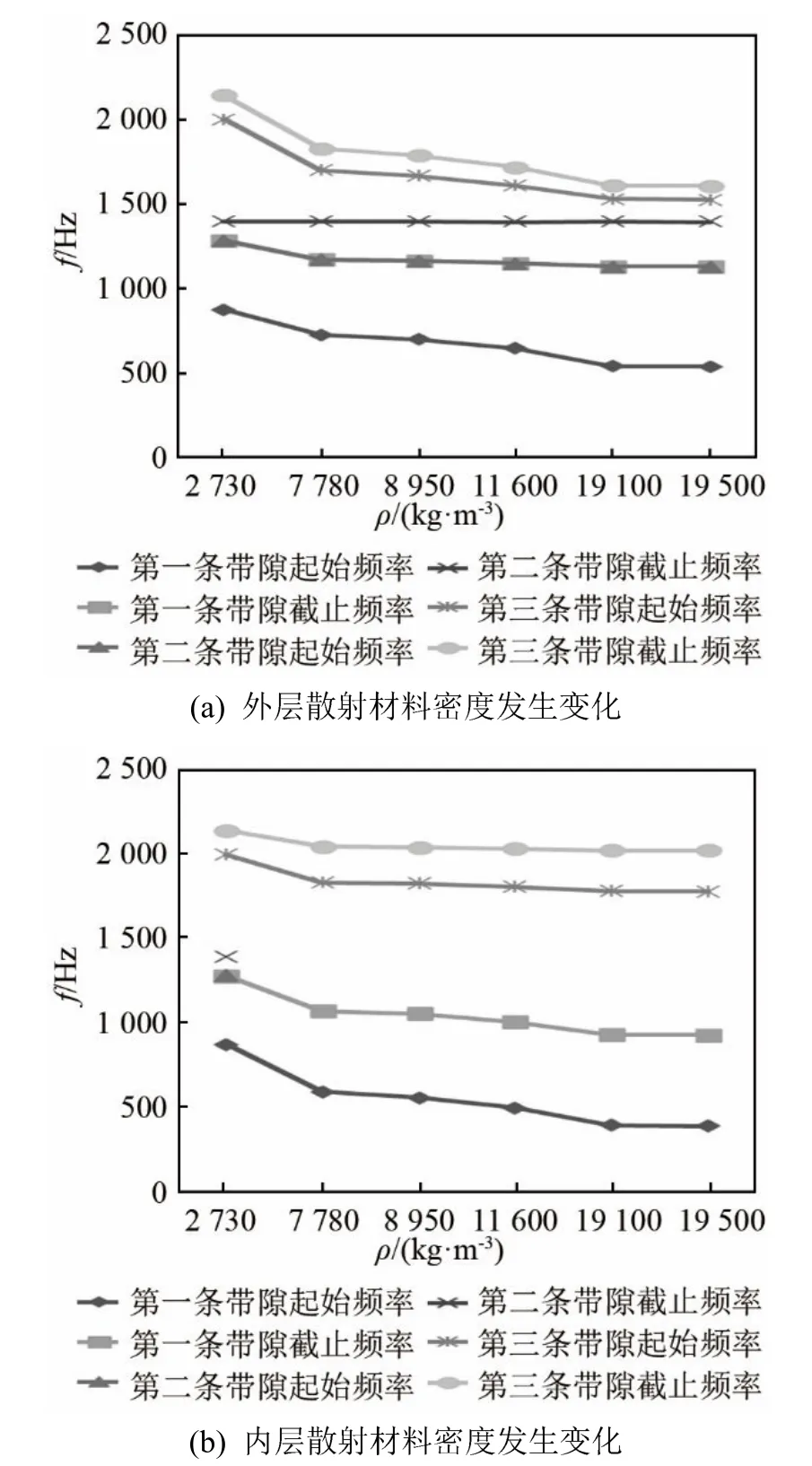
图14 散射体密度对带隙的影响Fig.14 Influence of scatterer density on band gap
(1) 保持内层散射体材料不变,只改变外层散射体材料,散射体密度对带隙的影响如图14(a)所示。由图14(a)可知,第二条带隙截止频率不会随着散射体的密度增加而改变,第一、三条带隙的截止频率以及第一、二、三条带隙的起始频率则会随着散射体密度的增加逐渐减小,且第三条和第一条带隙起始频率的减小幅度最大,而第二、三条带隙间的通带也逐渐减小,第一条带隙逐渐加宽,同时带隙频段逐渐向低频移动。
(2) 保持外层散射体材料不变,只改变内层散射体材料,散射体密度对带隙的影响如图 14(b)所示。由图14(b)可知,当内层散射体密度逐渐增加时,声子晶体第一、第二条带隙间的平直带与第二、第三条带隙间的通带合并,以致第一与第二带隙合并成一条宽带隙。随着内层散射体密度的增加,各带隙的起始、截止频率都逐渐减小,其中第一条带隙的起始频率减小幅度最大,因此第一条带隙的宽度逐渐变宽。当内外散射体密度差越大时,所产生的带隙越宽,同时带隙频段也逐渐向低频移动。
4.2 散射体几何尺寸对带隙的影响
从结构改变上来分析,在“弹簧-质量”系统中,等效质量的影响非常重要,在这里不考虑材料参数的影响,只考虑局域振子的几何尺寸的变化对带隙的影响,在计算过程中保持晶格常数a不变,基体框架不变,只改变包覆层和散射体的几何尺寸。
(1) 当外层散射体尺寸不变,柱状散射体的尺寸逐渐增大同时内层包覆层的尺寸减小所带来的带隙变化如图 15(a)所示。第一条带隙的起始频率基本不会发生改变。而随着柱状散射体边长的增大,第二、三条带隙的起始频率以及第一、二、三条带隙的截止频率逐渐增大。因此,可以看出第一条带隙的带宽逐渐增大。说明随着尺寸的变大带隙在向低频移动,频率相对高的频段的带隙开始逐渐变窄。
(2) 当柱状散射体尺寸不变时,外层散射体尺寸逐渐增大同时外层包覆层的尺寸减小时,其带隙变化如图15(b)所示,随着外层散射体边长尺寸的变大,各带隙起始点和截止点频率整体是逐渐增大的趋势,即带隙频段在逐渐往高频移动。当外层散射体与外层包覆层的厚度相当时,即外层散射体尺寸分别为10 mm和11 mm时,产生的带隙更宽。
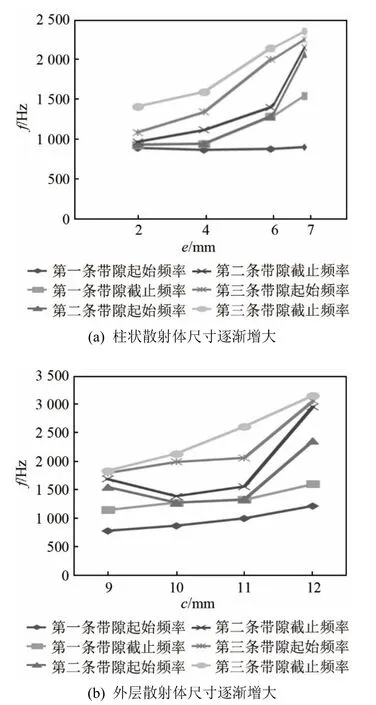
图15 散射体几何尺寸对带隙的影响Fig.15 Influence of the geometric size of scatterer on band-gap
4.3 散射体排列方式对带隙影响
以前的声子晶体中的局域振子是按照二维四方晶格排列方式排列的。为了能够实现宽频带隙特性,改变声子晶体的排列方式,参考互穿网络[13]结构提出一种交错排列结构的声子晶体,其结构如图16(b)所示。图16(a)中声子晶体的厚度设置与晶格常数值相同,使其之间没有缝隙。在声子晶体中,每层局域振子横纵交错排列,大大增加了共振模态,拓宽了共振频带吸收范围,吸声特性也相应增强,这种排列下声子晶体结构之间具有共振吸声、分子间摩擦吸声以及界面耗能多种机制。
本文利用COMSOL Multiphysics软件的固体力学模块计算声子晶体的传输特性曲线,方法与前面相同,通过传输特性曲线衰减的频率范围得到带隙范围,如图17所示。四方晶格排列方式如图16(a)所示,且对相同周期数的声子晶体在 0~5 000 Hz范围内的传输特性曲线进行对比,定义一个衰减阈值为0 dB。由图17可知,在2 000 Hz频率范围内,交错排列方式下的声子晶体有四处明显低于阈值的衰减,这些衰减区域为该声子晶体的带隙,而按四方晶格方式排列的声子晶体只有一个明显低于阈值的衰减,且该衰减区域的频率值要高于交错排列下声子晶体的第一个衰减区域频率值。这说明交错排列方式下的声子晶体容易产生更低频段的带隙。交错排列方式下的声子晶体的衰减区域频率段与四方晶格排列方式下的声子晶体衰减区域频率段相比,频段更加宽,这说明交错排列方式声子晶体会产生更加宽频的带隙,有利于实际应用。而在2 000~3 000 Hz频率范围内,四方晶格排列方式的声子晶体衰减区域的频段明显大于交错排列方式下的声子晶体,说明在这个频率范围内,四方晶格排列下的声子晶体能够更好地打开带隙。

图16 声子晶体结构Fig.16 Phononic crystal structure
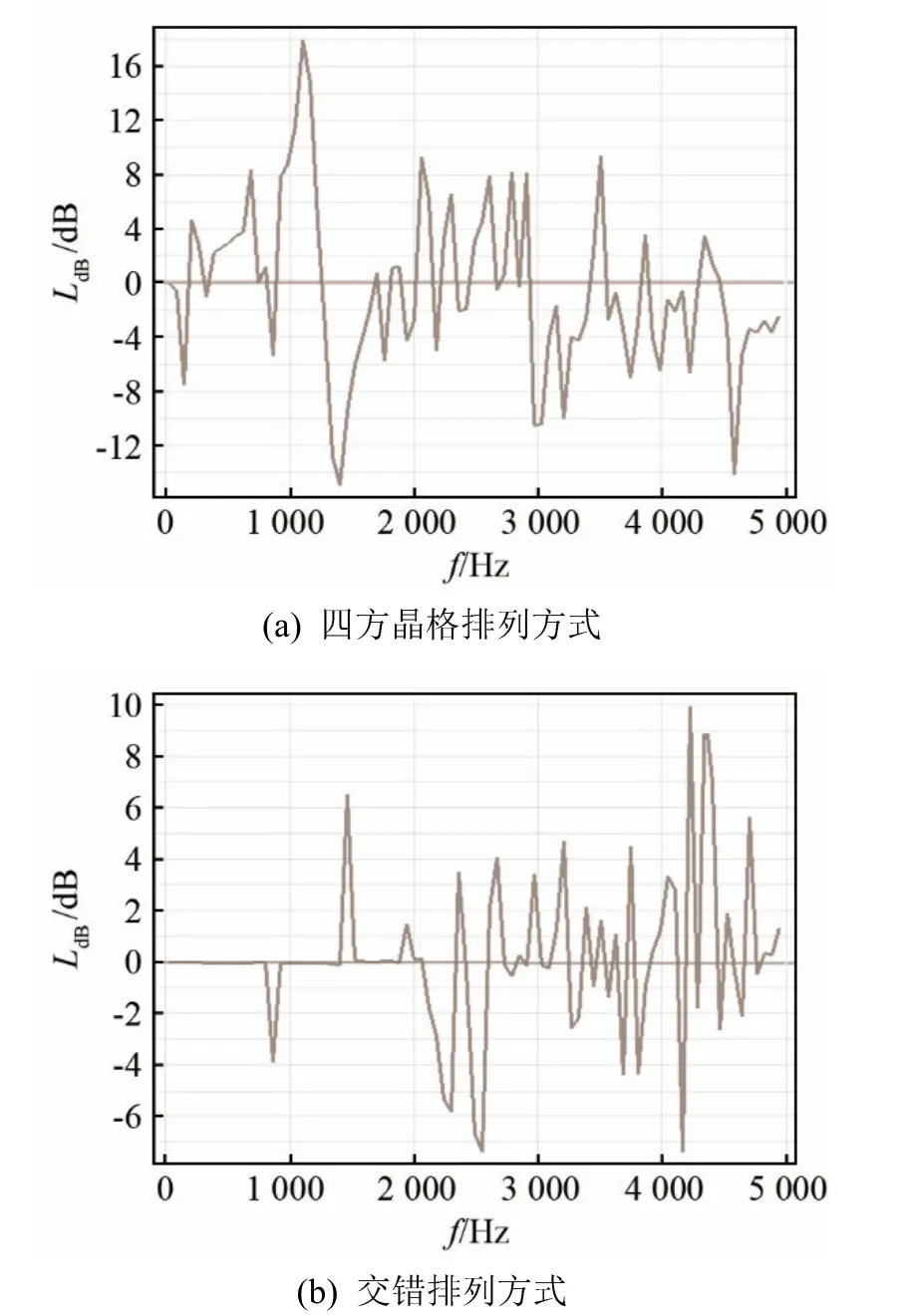
图17 不同排列方式下声子晶体的传输特性曲线Fig.17 Transmission characteristic curves of phononic cystal with different arrangements
综合以上三种影响因素,可以发现:等效质量越大,声子晶体所产生的带隙特性越明显,其带隙宽度也会增加。尤其是改变内层散射体材料密度时,带隙特性会更好。此外,当内、外局域振子的等效质量比达到一定值时,带隙之间的两个通带可以消失,进而形成一条宽带隙。而改变内外散射体材料的尺寸时,若只改变内层尺寸,则尺寸越大,等效刚度越大,带隙则越宽;只改变外尺寸,则当散射体与包覆层厚度相同时,带隙越宽,降噪效果就越好。当声子晶体散射体排列方式由四方晶格排列方式改为交错排列方式时,声子晶体更易于在低频范围打开带隙。
5 结 论
本文设计了一种新型的复合局域共振型声子晶体,该结构具有双层散射体与包覆层组成的局域振子,并使声子晶体的带隙频率在中低频段有明显的三条带隙。
首先,通过将声子晶体等效为弹簧-质量块的等效模型进行计算,估算出带隙频率,与有限元法结果进行对比验证,两者结果相近,并且该声子晶体结构在 2 200 Hz的频率附近产生三条完整的带隙,其中一条是带宽达到406.17 Hz的宽带隙,而通带在此频率范围中的占比为45.71%。
其次,基于有限元法计算了该局域共振型声子晶体的振动模态,并分析了带隙产生的原因。计算与测试结果表明:共振带隙频率位置取决于其共振模态的固有频率,而带隙宽度则与局域共振模态和基体之间的相互耦合有关。
最后本文分析了影响带隙的因素。研究表明,改变各影响因素,可以调节局域共振模态的固有频率,达到调控带隙边界上下频率的目的。此外,等效质量越大得到的带隙频率越向低频移动。调节内层局域振子的等效质量,第一带隙频率的变化幅度较大;调节外层局域振子等效质量,第三带隙频率的变化幅度较大。后续可以通过改变内、外层局域振子的等效质量比,使带隙合并成一条更宽的带隙;研究还发现,改变晶体排列方式后,交错排列方式下的声子晶体更容易在低频段打开带隙,这为获得宽低频带隙提供了一种新的思路和方法。

