基于变分模态分解的水下目标噪声特征提取及分类

鞠东豪，李 宇，张万达，张春华

(1. 中国科学院声学研究所，北京100190；2. 中国科学院大学，北京100039；3. 中国科学院先进水下信息技术重点实验室，北京100190；4. 中国船舶工业系统工程研究院，北京100036)

0 引 言

近年来，随着各类航行器的发展以及各类传感器的更新迭代，海洋航行和探测识别领域取得了很大的进步。目标分类识别算法是水下探测技术的关键一环，也是声呐的一项重大任务，传统的目标识别技术往往依赖于声呐兵的经验进行判断，但是随着探测技术的发展和传感器数目大量增加，以及各类无人航行器的发展，人工识别渐渐被淘汰。

目标识别可以分为两部分进行，其一是对目标进行特征提取，即对接收数据使用信号处理手段突出其代表性特征。其二是分类器设计，即对目标特征进行学习和分类。其中特征提取算法的优劣往往直接决定了目标识别的成功率，因此特征提取是水声被动目标识别的关键任务。1997年章新华等将目标特征提取和小波分析和功率谱分析结合，使用BP神经网络进行分类[1]，取得了较好的分类效果。2002年李亚安等利用水下噪声信号的混沌现象提取其混沌特征[2]。此外，还有学者受人耳识别的启发，利用梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficient, MFCC)特征进行目标的识别[3]，同样有较好的效果。

1998年，黄锷提出了希尔伯特-黄变换(Hilbert-Huang Transform, HHT)[4]，该变换被称为经验模态分解算法(Empirical Mode Decomposition, EMD)。这是一种检测并且将信号分解为各阶模态的方法。这一方法依赖对信号极值点的寻找、极值点的插值以及停止准则，且该方法缺乏数学理论的支撑，综上几点原因该方法的鲁棒性还有待提高。EMD算法虽然存在一些弊端，但是影响十分广泛，在医学、生物学等多个领域均有应用。2007年王锋等将HHT方法引入水声信号处理中[5]，对四类目标进行分类实验，达到了 90%以上的识别正确率。另外针对EMD算法存在的模态混叠问题，有学者将集合经验模态分解算法(Ensemble Empirical Mode Decomposition, EEMD)和希尔伯特边际谱相结合[6]，一定程度上解决EMD分解时出现的模态混叠问题。Dragomiretskiy等于 2014年提出了变分模态分解(Variational Mode Decomposition, VMD)算法，该方法自适应地切割信号频段，有效解决了传统EMD算法中模态混叠的问题[7]。

为了提升目标识别的效率，本文将VMD引入水声目标分类当中，结合希尔伯特变换算法形成21维特征向量，通过对比多类分类器实验，结果表明VMD-HT联合处理算法具有更高的分类正确率。

1 特征提取算法

1.1 变分模态分解

传统 EMD算法的本征模函数(Intrinsic Mode Function, IMF)被定义为一个局部极值和过零点个数最多相差1的信号。VMD算法对IMF的定义稍做改动，VMD算法认为 IMF是调幅调频信号(AM-FM)[7]，记为

式中：uk(t)为第k阶MF分量，其中第k阶MF分量的相角是一个非递减函数，即，第k阶MF分量的幅值是非负的函数为时间。在足够长的时间段模态uk( t)可以被视为是一个振幅为Ak( t)、瞬时频率为φk′(t ) 的纯谐波信号。不难发现，上述这一定义比最原始的IMF定义更加严格。

VMD分解的目的是将原始输入信号 f分解为多个符合上述模型的 IMF分量uk。假设每一个IMF分量uk是围绕着某一个中心频率ωk振动产生的，而这一中心频率是在分解过程中确定的。对每一个IMF uk( t)进行希尔伯特变换，利用指数修正得到K个模态函数，将模态函数频谱修正到估算的中心频率，利用高斯平滑计算出模态分量的带宽[7]：

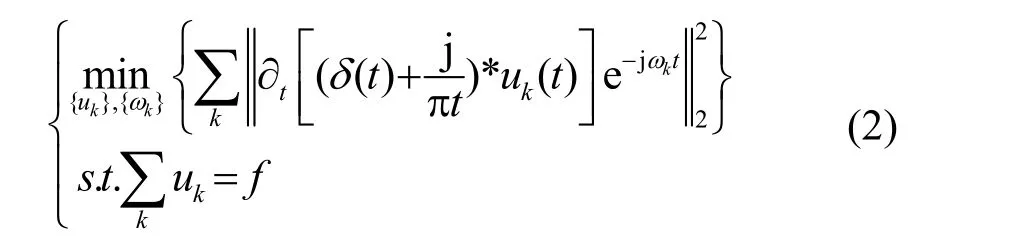
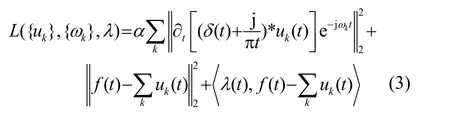
使用乘法算子交替算法(Alternating Direction Method of Multipliers, ADMM)求式(3)的鞍点，更新uk如式(4)所示：

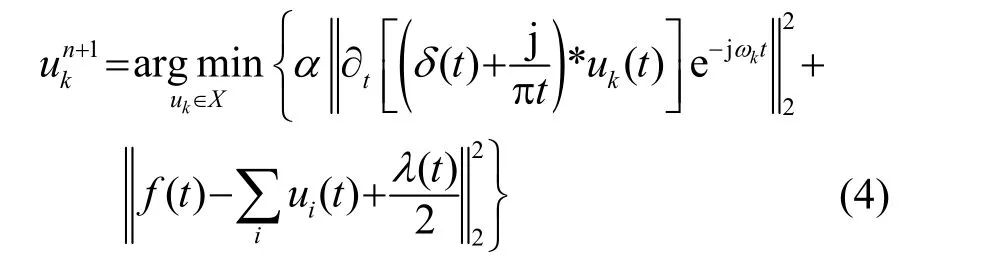
式中：α为惩罚因子；λ为拉格朗日乘子；X为f和uk所在的函数空间。使用 Parseval/Plancherel傅里叶等距变换，将式(4)转换到频域，如式(5)所示：

该算法在分解信号的过程中不断自适应的更新每个IMF分量的中心频率，可以有效地避免传统EMD分解算法中的模态混叠现象，减少无效分解数量，且不同于EMD算法的是，该方法具有详细完整的数学推导过程。

1.2 基于VMD-HT变换的水声信号特征

水声被动目标识别过程如图1所示。

图1 水声被动目标识别算法流程图Fig.1 Flow chart of the classification algorithm for ship radiation noise

如1.1节所述，对信号进行VMD分解后，为了更好地反映数据的瞬时性，对分解后的各个分量进行Hilbert变换处理，可以得到各个分量的瞬时振幅和瞬时频率，如式(9)所示：

由信号的瞬时相位可以求得其瞬时频率如式(12)所示：

由经过希尔伯特变换的IMF分量的瞬时频率、边际谱以及幅值等特征经过组合构成 VMD-HT特征。仿真数据的时域信号如图2所示。

将图2所示的时域信号分别进行短时傅里叶变换和VMD-HT变换后的时频图，如图3所示。

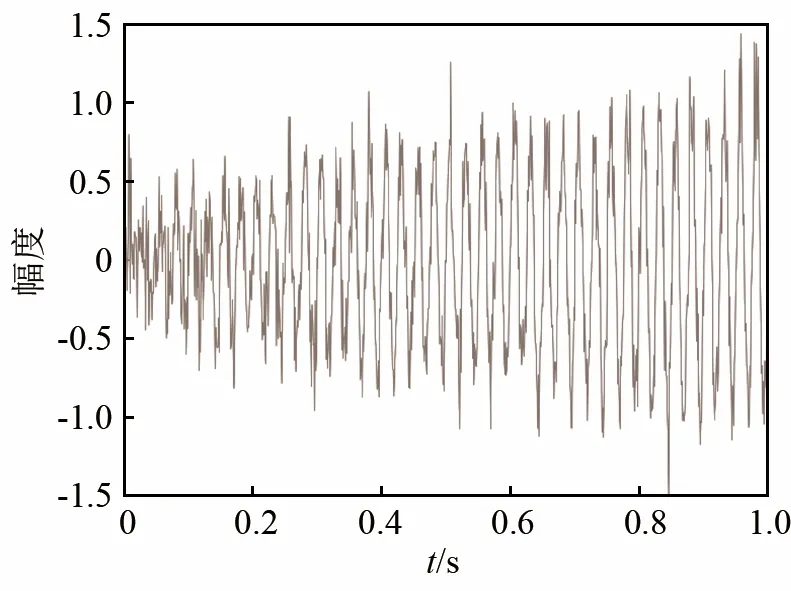
图2 仿真数据时域信号Fig.2 Time domain signal of simulation data

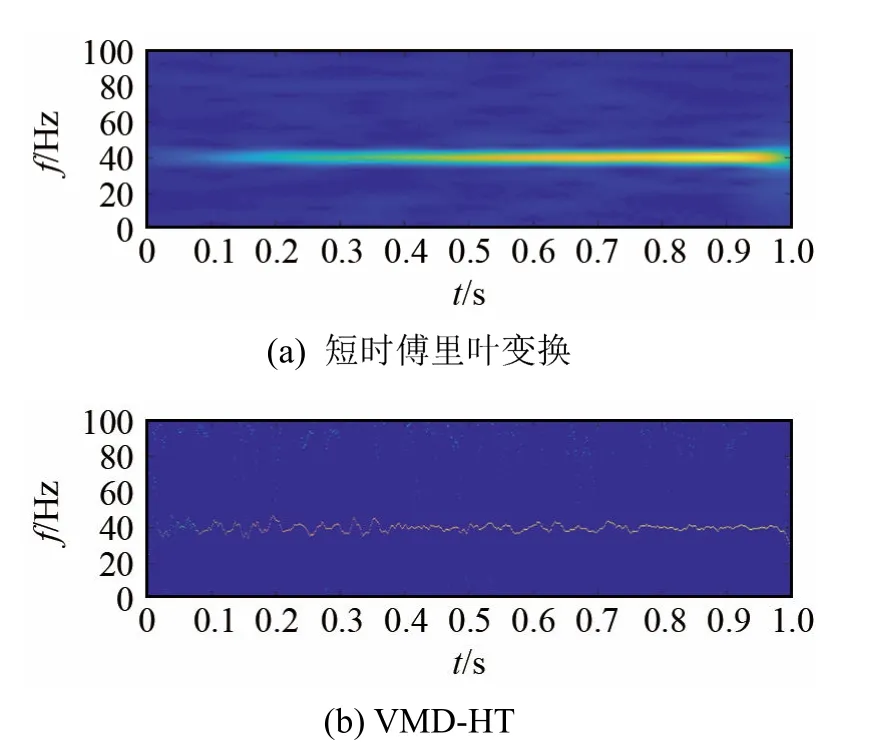
图3 仿真数据短时傅里叶变换以及VMD-HT的时频图Fig.3 The time-frequency diagrams of short-time Fourier transform of simulation data and VMD-HT

由图3不难看出，VMD-HT算法所绘制的时频谱图相比于短时傅里叶变换时频谱可以更好地描述信号的随机扰动。

1.3 模态选择

VMD各阶模态中是否存在干扰模态以及如何将干扰模态剔除是十分值得研究的问题。干扰模态不仅增加特征维数，影响分类器效率，很大程度上也容易混淆目标特征，从而影响对目标的分类，所以需要在特征提取之前将干扰模态剔除。本文使用相关性作为区分依据进行干扰模态的剔除。以渔船噪声为例，渔船噪声的原始时域信号以及VMD分解结果如图4所示。对图4中的各阶IMF分别计算其与原信号的相关系数结果如图5所示。通过将每一阶 IMF和原始信号的相关系数与阈值(本文设定为0.1)对比，不难看出，对于图4中的渔船数据而言，应当保留1～3阶IMF进行特征提取，而4～10阶IMF则被视为干扰模态被剔除。使用这一方法能够一定程度上提高特征提取算法的效率和分类器的分类正确率。

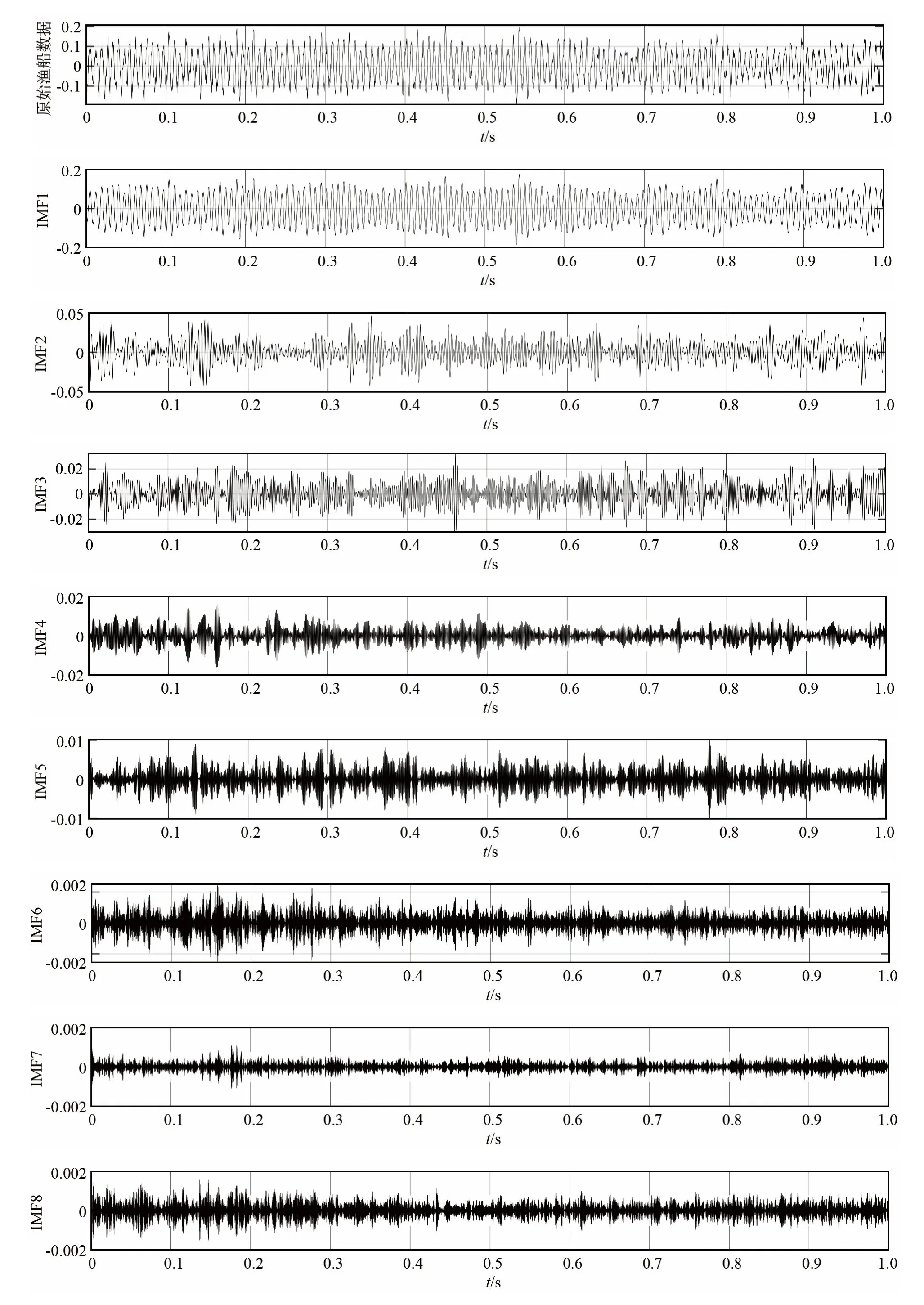
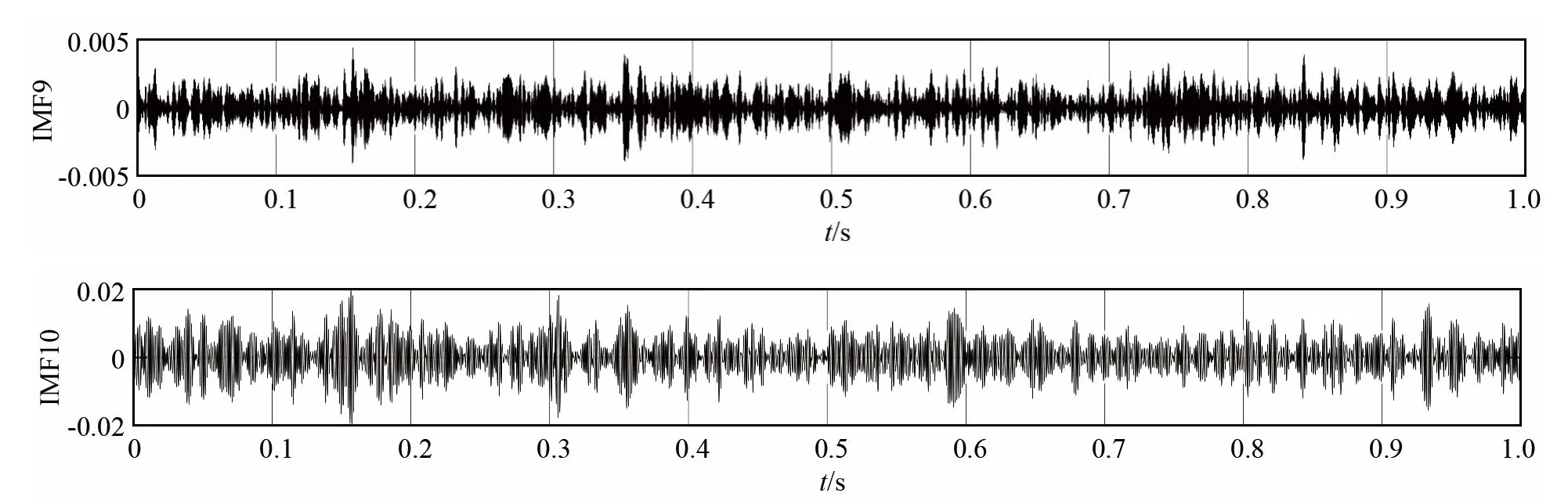
图4 渔船噪声原始时域信号以及VMD分解结果Fig.4 Original time domain signal and VMD decomposition result of fishing boat noise

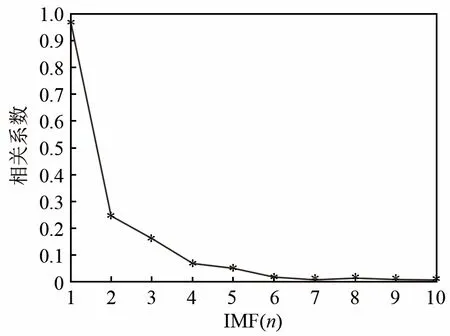
图5 渔船噪声各阶本征模函数（IMF）与原始信号相关系数Fig.5 Correlation coefficients between each order of IMF and original signal of fishing boat noise

2 目标分类算法

2.1 分类算法简介

水下目标分类常用的分类器算法有：K最近邻(K-Nearst Neighbor, KNN) 算法、随机森林(Random Forest, RF) 算法、朴素贝叶斯(Naive Bayes, NB)算法、人工神经网络(Artificial Neural Network, ANN)算法以及支持向量机(Support Vector Machine,SVM)算法。水声目标分类由于样本数量有限的原因容易出现过学习和欠学习的现象。支持向量机算法所构建的分类规则能够很好地平衡算法的性能和推广能力，既能适应复杂多变的水下环境，又能够保证较好的分类效果，所以本文应用支持向量机算法对目标进行分类。

2.2 支持向量机算法简介

支持向量机源于结构风险最小化理论，首先利用核方法将输入空间样本经过非线性变换映射到高维空间中，然后在从高维空间中寻找最优超平面进行分类，这一过程可以将一个复杂的分类问题极大简化。所谓最优超平面就是要求该超平面不仅可以将两类数据分开而且分类间隔最大，这种具有最大分类边界的分类算法具有更好的泛化能力。

式中：x是输入向量，w是可调权值向量，b是偏置。由式(13)可以写出：

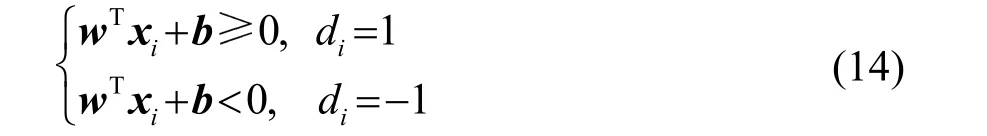
对于给定的w和b，决策曲面与最近数据点之间的间距被称为分离边缘ρ。支持向量机算法核心在于如何寻找分离边缘ρ最大的决策曲面，决策曲面被称为最优超平面。通过上述原则可以构造出线性支持向量机的最优化问题：

可以通过求解上述凸二次规划问题得到目标支持向量机额最优权值w*和偏置b*。

对于线性可分的样本，很容易确定最优超平面，但是当样本类别以非线性的形式分散时，线性边界就变得不再适用。可以使用某种映射函数将输入向量投影到可线性分类的高维的特征空间中，从而解决这一非线性分类问题。这种映射函数被称为核函数，核函数的选取需要满足Mercer定理，在这里列举三类常用核函数作为例子[8]，如表1所示。

表1 支持向量机(SVM)常用核函数Table 1 Common kernel functions for SVM

3 实验验证

3.1 特征提取

本文提取多类基于VMD分解的数据特征，特征类型及对应向量维数，如表2所示。

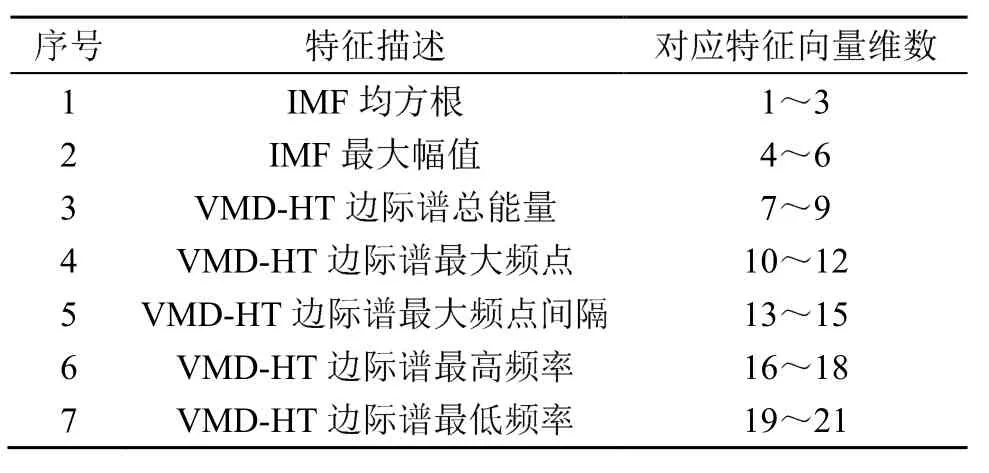
表2 特征类型及对应向量维数表Table 2 Feature types and corresponding vector dimensions

3.2 实验结果

使用某航次数据作为数据集。该数据集中包括三类不同型号的舰船目标辐射噪声，分别提取目标信号EMD-HT、EEMD-HT以及VMD-HT三种类别特征作为分类器输入，分别使用K近邻分类器、随机森林分类器、朴素贝叶斯分类器以及由一对一法构建的支持向量机多分类器共四种分类器进行对比分析，结果如表3～5所示。

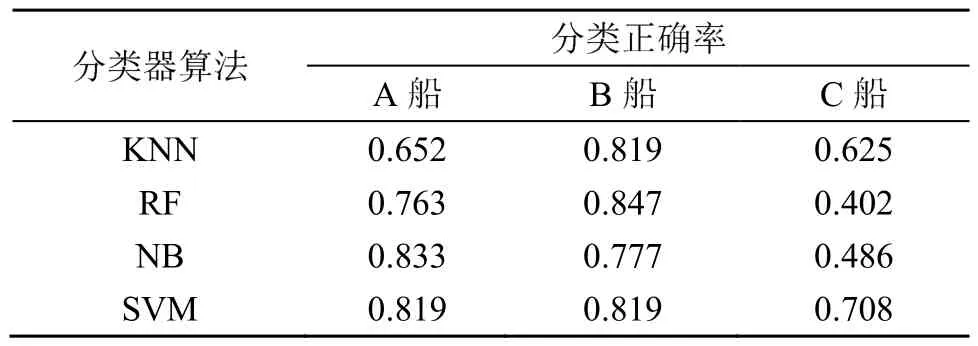
表3 不同分类器基于EMD-HT特征分类结果(某一航次数据)Table 3 Classification results of different classifiers based on EMD-HT features (data from a certain voyage)

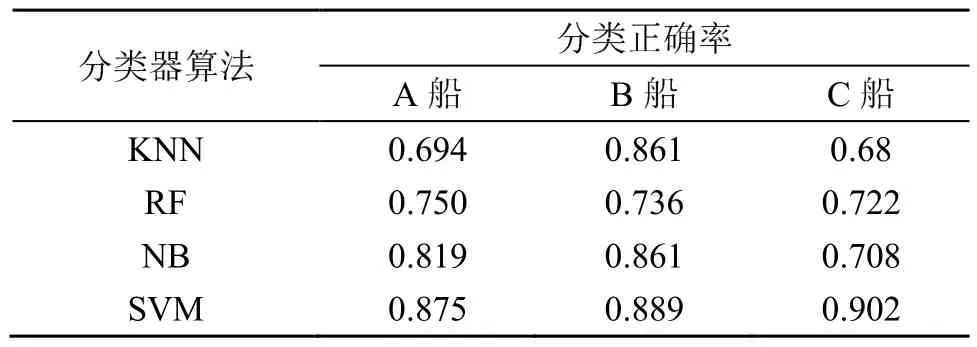
表4 不同分类器基于EEMD-HT特征分类结果(某一航次数据)Table 4 Classification results of different classifiers based on EEMD-HT features (data from a certain voyage)

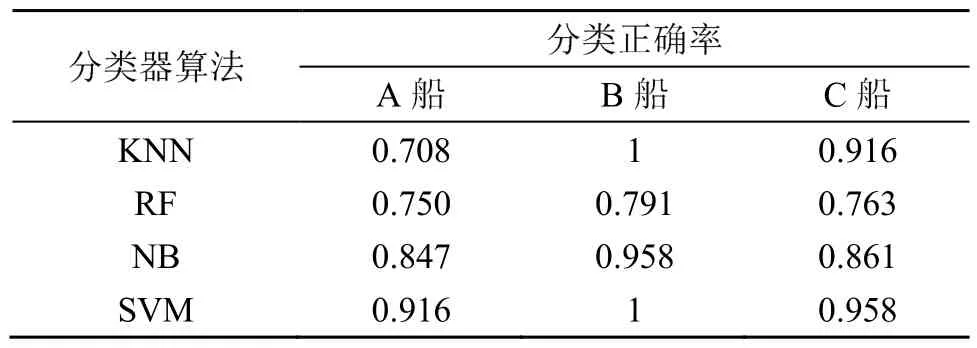
表5 不同分类器基于VMD-HT特征分类结果(某一航次数据)Table 5 Classification results of different classifiers based on VMD-HT features (data from a certain voyage)

为了更好地验证 VMD-HT算法的鲁棒性，选取同次海试不同航次的数据作为测试集，分类结果如表6～8所示。

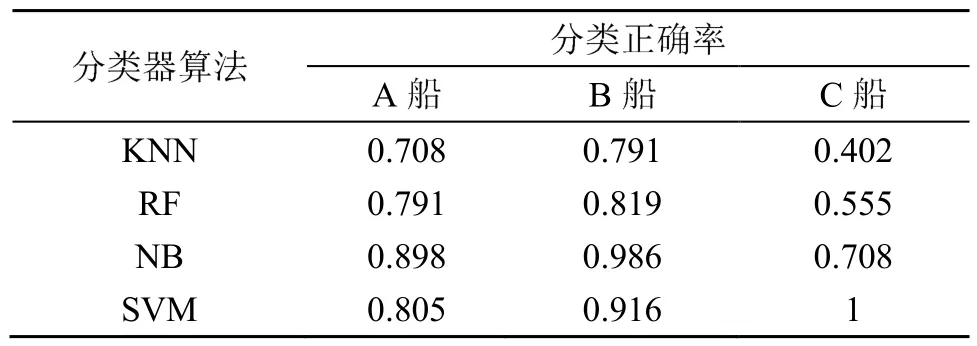
表6 不同分类器基于EMD-HT特征分类结果(另一航次数据)Table 6 Classification results of different classifiers based on EMD-HT features (data from another voyage)

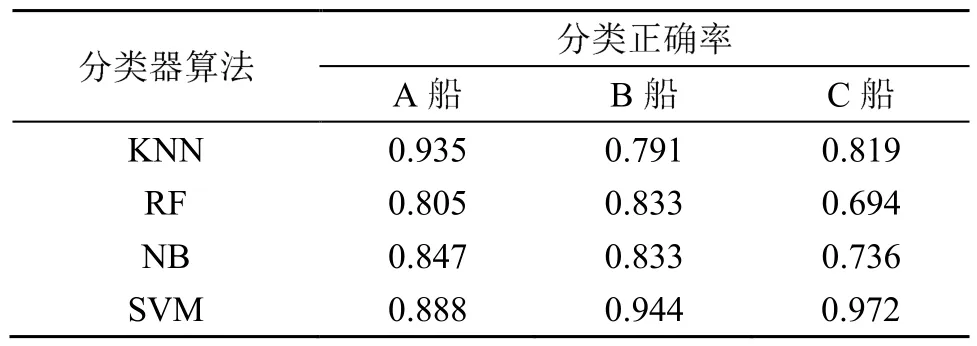
表7 不同分类器基于EEMD-HT特征分类结果(另一航次数据)Table 7 Classification results of different classifiers based on EEMD-HT features (data from another voyage)

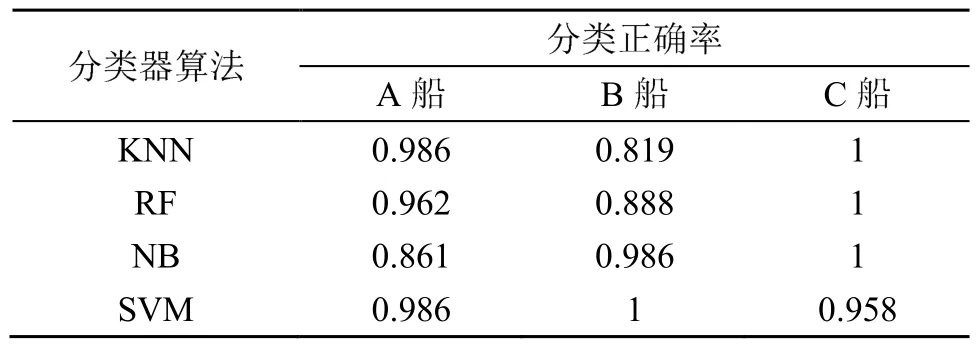
表8 不同分类器基于VMD-HT特征分类结果(另一航次数据)Table 8 Classification results of different classifiers based on VMD-HT features (data from another voyage)

由上述对比分析结果可见，VMD-HT算法对各类目标的分类准确率比EMD-HT以及EEMD-HT算法都有一定的程度的提高。EEMD一定程度上避免了模态混叠问题，识别正确率有了一定的提升；而 VMD-HT算法一方面解决了模态混叠的问题，同时也保证了 IMF信号的完整性。综上所述，VMD-HT算法对各类目标的分类正确率都高于其他几类分类算法。因此使用VMD算法进行水下目标的分类，可以有效提升对水下目标的分类效果。此外，由对比分析还可见，SVM分类器在分类准确度方面要高于KNN、RF以及NB三类分类器。

4 结 论

本文使用变分模态分解算法结合希尔伯特变换来构造目标信号特征集，基于分解后的干扰信号数据，采用设定相关系数阈值剔除干扰模态的方法，对比KNN、随机森林、朴素贝叶斯以及SVM四种分类器的对EMD-HT、EEMD-HT和VMD-HT三种特征集的分类效果表明，其中 VMD-HT算法提取的特征分类正确率最高，此外还针对训练出的分类模型使用不同的航次数据进行了验证，得到了相同的结论，可见本文 VMD-HT特征集用于水下目标被动分类具有良好的应用前景。