基于petri网的网络互助平台业务流程模型优化*
李多芹
(安徽理工大学数学与大数据学院,安徽 淮南 232001)
0 引 言
随着生活水平的不断提升,人们对重大疾病的预防也越来越重视。然而,标准的重疾险因费用高昂并不能很好的普及,从而门槛低、投资小的网络互助平台随之兴起[1,2]。为了网络互助平台更好的发展,提升服务质量、优化服务流程并最大限度的发挥平台的作用是十分重要的。petri网是建立和分析流程模型的工具,特别便于描述系统中事件的顺序、并发及冲突等关系。因此,关于petri网很多学者做了大量的研究,其中文献[3]指出了petri网的适用领域及发展趋势。文献[4]中以petri网关联矩阵为基础,展示了其在流程模型分析中的独特作用。文献[5]中从petri网的进程角度研究行为一致性问题。文献[6]表明出现网对于petri网研究有着重要意义。此外,基于petri网的优势,不少学者利用其对流程问题进行建模并对所建模型进行优化,并得出了具有实际意义的优化结果[7,8]。基于此,利用上述相关概念,基于petri网对互助平台的服务流程系统进行建模分析并提出了优化方案。
1 基本概念
定义1[4](关联矩阵)
设Σ=(S,T;F,M0)为一个petri网,则petri网Σ的结构(S,T;F)可以用一个n行m列矩阵A=[aij]n×m来表示,其中

j∈{1,2,…,m},称A为Σ的关联矩阵。
定义2[6](出现网):
设Ν=(B,E;G)为一个网。如果
1)∀b∈B:|·b|≤1∧|b·|≤1;2)∀x,y∈B∪E:(x,y)∈G+→(y,x)∉G+
则称Ν为一个出现网,其中G+表示流关系G的传递闭包。
定义3[5](petri网进程)
设Σ=(S,T;F,M0)为一个petri网,Ν=(B,E;G)为一个出现网。如果petri网到出现网的映射φ:N→N满足条件:
1)∀b1,b2∈B,b1≠b2:φ(b1)=φ(b2)→·b1≠·b2∧b1·≠b2·
2)∀s∈S:|{b|φ(b)=s∧·b=φ}|≤M0(s)
则称(Ν,φ)为Σ的一个进程。
定义4[7](状态方程)
设Σ=(S,T;F,M0)为一个petri网,其中M0为初始标识A为Σ的关联矩阵,若M∈R(M0),则存在非负整数向量X,使得
M=M0+ATX
(1)
(1)式称为petri网的状态方程。
2 基于petri网的分析及优化
2.1 服务流程系统的建模
利用petri网对某一网络互助平台的服务流程系统进行建模,如图1所示,图中模拟了用户申请加入平台、加入成功后按期分摊并进入等待期、等待期结束、申请互助及申领互助金等整个流程。
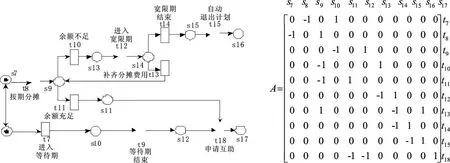
图2 网Σ=(N1,M0)及N1的关联矩阵A
由图1可知,用户加入互助平台需要先申请,即t1发生,接着t2发生判断用户是否满足加入条件。若t5发生则t6发生成功加入。成功加入后立即进入等待期,同时履行按期分摊的义务,即发生t7和t8,t7发生90天后等待期结束,即发生t9;t8发生后引发t10或t11。若t11发生,余额充足则正常进行按期分摊;若余额不足t10发生,到分摊日后会发生t12,进入宽限期。此时若在15天内补齐分摊费用,即发生t13,则会回到正常分摊状态;若用户没能在15天之内补齐费用则发生t14宽限期结束,接着发生t15,自动退出互助计划。此时,用户可以选择发生t16或t17。
只有在t9和t11同时发生后t18才有权发生,即只有等待期结束且账户余额充足时才能申领互助金。接着t19发生,若平台不同意该申请则t20发生,引发t21,用户回到正常分摊且等待期结束的状态;若同意该申请则t22发生,接着会发生t23,向用户发放互助金同时发生t24自动退出计划,流程结束。
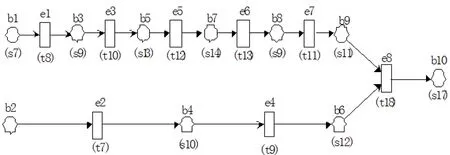
图3 Σ=(N1,M0)两个变迁序列σ(左)和σ'(右)的进程
2.2 原petri网模型正常运行的验证
易知图1中的petri网为纯网,因此我们可以利用关联矩阵描述其结构。因为当我们以参与成员的总数为基数时,真正成功申领互助金的成员数量是很有限的,所以这里只描述按期分摊及等待期部分的流程。记图1中虚线部分的网为N1,则网Σ=(N1,M0)及N1的关联矩阵A如下:
对网N1,由图2可知初始标识M0=[1,1,0,0,0,0,0,0,0,0,0],变迁序列σ=t7t8t9t11t18发生后的可达标识为M=[0,0,0,0,0,0,0,0,0,0,1],利用状态方程M=M0+ATX的求解寻找满足状态方程的非负整数向量X。因为rank(AT)=rank([AT,M-M0])=10,所以可得唯一解X=[1,1,1,0,1,0,0,0,0,1]。正好与σ中的变迁序列一一对应,因为X中的第i个分量等于ti在σ中出现的次数。即存在非负整数向量X满足状态方程,故网N1满足定理1,从而验证了petri网模型能够正常的运行。
发现在初始标识M0下若发生变迁序列σ′=t7t8t9t10t12t13t11t18,可达标识也为M。易知在变迁序列σ和σ′中都存在着并发的变迁序列,而petri网进程的引入正是为了反映系统中的并发行为,下面用出现网表示网N1从M0到M的两种运行轨迹。
2.3 对服务流程的优化
由图1可以发现:
1) 申请加入互助平台需要满足一定的条件。其中一项要求用户有一定的信用积分,这对于部分人群来说是难以达到的。此时,可以邀请已加入该互助平台的第三方用户担保加入。
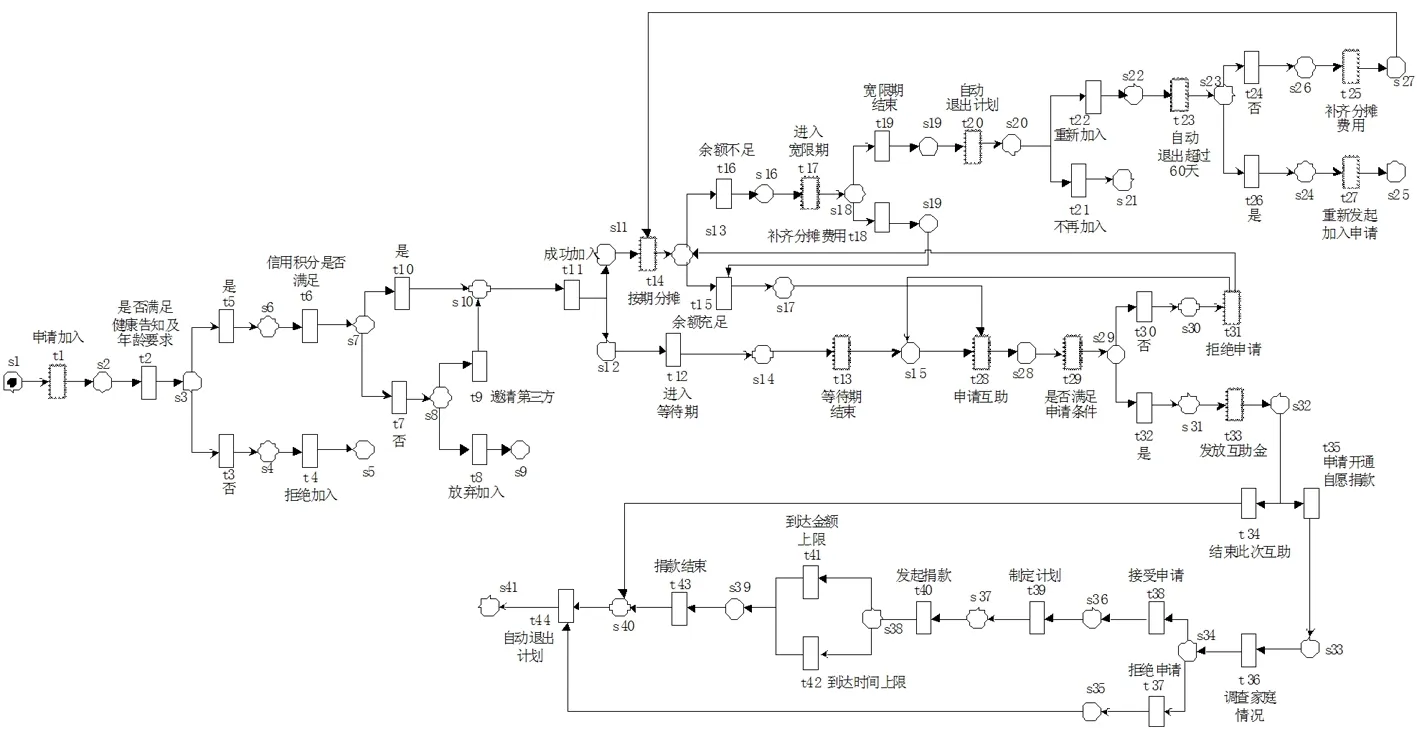
图4 某互助平台服务流程系统网优化模型
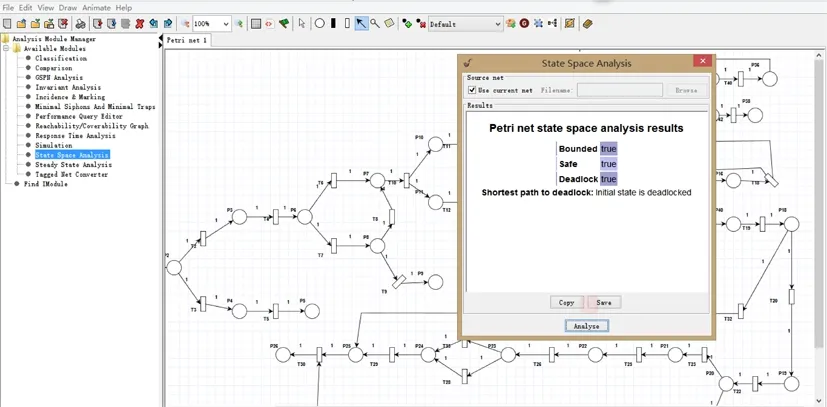
图5 图4中模型的拟运行结果
2) 宽限期一般只有15天,期满后会自动退出。被动退出后,用户若选择重新加入,还需要再次经历90天的等待期,这对长期参与分摊的成员是不公平的。这时可以加以控制,宽限期满后被动退出60天内重新加入的,不需要再次经历90天的等待期,但要支付宽限期及退出期间应分摊的费用;被动退出超过60天的,按原计划实施。
3) 发放互助金后会自动退出计划。但若是重大疾病,花费远超互助金额且家庭情况难以承受的,这样直接结束互助没有使平台最大限度的发挥其作用。这时可以在平台内开通自愿捐款平台,设置捐款时限和金额上限,到期或捐款金额达到上限后自动结束互助。
根据上述三点进行优化,优化后的服务流程模型如图4所示:
1)为了吸引更多人加入,在原模型上增加了变迁t3至t10,增设引入第三方做担保的加入流程,合理的放宽了加入条件,扩展平台成员数量的同时使得该计划能惠及更多需要帮助的人;
2)合理延长宽限期并且通过增加变迁t23,t24,t25,让意外被动退出60天内的成员以更加人性化的方式重新进入;
3)优化针对于特殊情形的互助,在原模型上增加了变迁t35至t43,增设自愿捐款平台,参与互助计划的其他成员可自愿为申领过互助金的用户捐款。
3 仿真实验及结果分析
为了验证图4所示优化后模型的性质,利用仿真软件Pipe对优化后的Petri网流程模型进行分析。首先,在软件工作台上绘制优化后的流程模型,然后使用”state space analysis”分析工具对模型进行分析。分析结果显示优化后的模型是有界且安全的,如图5所示。这说明优化后的模型是合理可行的,且为网络互助平台中存在某些问题提供了初步的优化方案。
4 结 语
网络互助是近年来兴起的新的商业模式和投保选择,因其低成本等独特的优势受到很多大众,尤其是年轻人的喜爱和认可。为了吸引更多的用户,各平台都在不断累积经验、优化服务流程。 为了更好的服务大众,针对某一平台先利用Petri网模拟其服务流程,结合相关知识验证模型的正常运行,接着从加入条件、宽限期处理及互助延伸三个方面对其服务进行优化,使得该平台的服务流程更加完善、合理,从而能有力的扩展其成员,这对平台和大众来说都是有益的。
基于Petri网,通过在原模型中增加控制结构,对整体的流程框架进行了优化。但更细节的,如:审核申领材料的流程及调查家庭情况的流程等还需要进一步的优化,以防止不法分子投机取巧,为了一己私利,提供虚假材料。使得平台中的每位成员在帮助他人的同时也能保护自己的利益,同时在自己需要帮助的时候得到支援。

