基于轮对磨耗数据的CRH2A 型动车经济镟修策略研究

张 渝，王 松，邱春蓉

（西南交通大学 物理科学与技术学院，成都 610031）

随着我国铁路的飞速发展，动车、客车、机车的开行数量、速度和载荷都迅速增加，对列车车轮的品质和质量状态提出了更高的要求。若不及时准确发现列车车轮问题，将给铁路运营带来安全隐患，给国家财产带来巨大损失[1]。因而，准确地预测列车轮对磨耗量，进行镟修判断，优化列车轮对镟修策略，对我国列车维修和铁路安全具有重要意义[2]。

列车轮对作为列车安全行走的关键部件，一直是国内外学者的研究热点[3]。Pradhan S 等人研究了印度铁路存在的轮对磨耗问题，并做出预测，但没有提出使用数理统计处理数据[4]；Pascual 等人通过对随机抽样的1 000 多个美国在役列车车轮磨耗进行统计分析，发现轮缘厚度与轮缘磨损的速率成正比[5]；王凌等人通过追踪轮对和镟修成本，研究列车运行成本以月为单位的计算方式，完善了经济镟修策略的评价手段[6]；杨志采用数理统计的方式，建立了轮径的正态模型，利用蒙特卡罗方法生成随机的轮径月磨耗量，仿真出镟修策略的生命周期和镟修次数[7]；徐文文[8]等人研究了地铁受电弓滑板的磨耗趋势并进行有效预测，节约了地铁的运营和维修成本，为动车的经济镟修提供了新的研究思路。

需要指出，数理统计模型的拟合度对于镟修策略仿真的正确性至关重要[9]。拟合度越低，数理统计的轮径模型与实际磨耗值偏差越大。在蒙特卡罗仿真中，使用轮径模型来随机生成当月的磨耗仿真值，随着仿真进行，轮对运用月数越多，离正确的镟修策略偏离越大。为解决上述问题，本文提出一种优化的分布拟合模型来分析经济镟修策略。

1 方法概述

1.1 蒙特卡罗仿真

本文利用蒙特卡罗仿真方法，模拟动车在真实运行周期中轮对每月的磨耗，从而计算得到该轮对的生命周期以及镟修次数。

蒙特卡罗仿真是指，当所求问题建立在某随机数列之上，或和随机数列相关时，可采用拟合分布生成伪随机数列的方式来模拟实际情况[9]。其仿真的主要过程包括3 部分：（1）构造或描述概率过程；（2）实现从已知概率分布抽样；（3）建立各种估计量。

1.2 拟合结果评价指标

为准确评价模型的拟合程度，本文选择相关性系数（R）、均方误差（MSE，Mean Squared Error）、平均绝对误差（MAE，Mean Absolute Error）、平均绝对百分误差（MAPE，Mean Absolute Percentage Error）、方差（SSE，The Sum of Squares due to Error）作为衡量预测结果精度的标准。具体计算公式如下：式中，ER为相关性系数；EMSE为均方误差；EMAE为平均绝对误差；EMAPE为绝对百分误差；ESSE为方差，Yi为真实值；为模型预测值；分别是真实值和模型预测值的平均值；wi为各项数据权重；n为预测样本数。MSE、MAE 及MAPE 值越小，表示模型拟合精度越高；R 值越接近1，表示模型拟合精度越高。

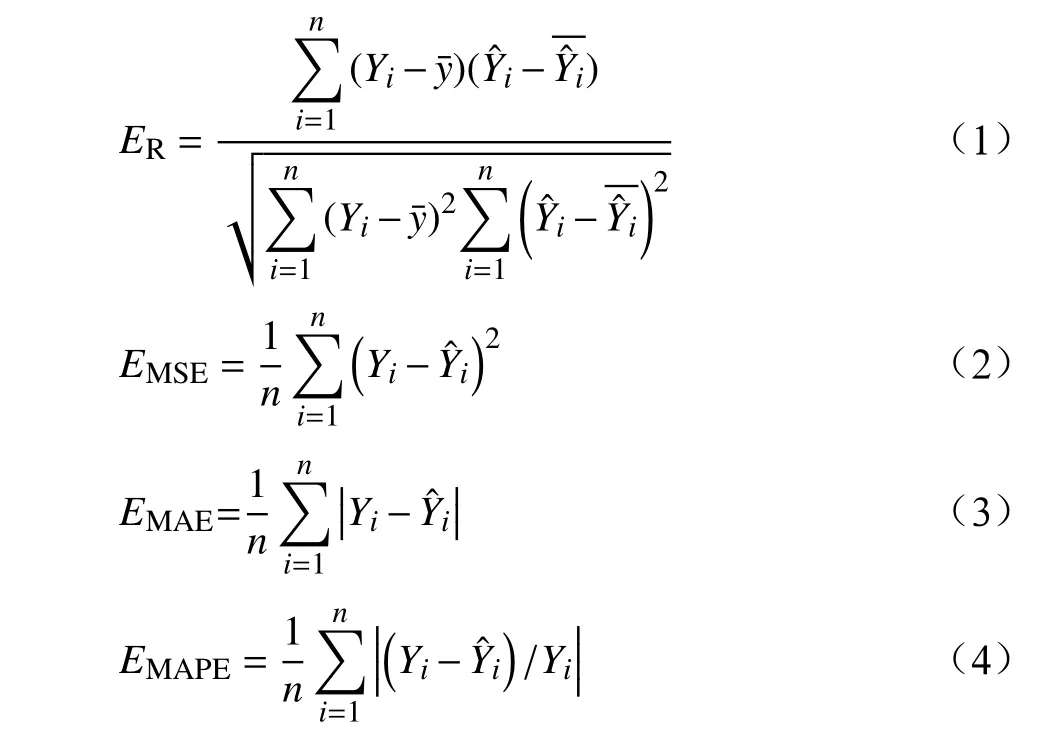
2 建立轮对磨耗模型

2.1 轮缘厚度磨耗建模

为制定更合理的轮对镟修策略，本文根据轮对磨耗的历史数据研究轮对的磨耗规律。使用SPSS 软件分析得到轮对磨耗数据之间的皮尔森相关性，其中，轮缘厚度和轮缘厚度磨耗速率的皮尔森相关系数为−0.293 2，认为两者是相关的；轮径和轮径磨耗速率的皮尔森相关系数为−0.093 2，则认为两者是独立的，因此使用轮缘厚度和轮缘厚度磨耗速率建立模型。

本文使用CRH2A 型动车组于2017 年 — 2019年8 个轮对的轮缘厚度数据作为样本数据，建立磨耗模型，该车轮轮缘厚度的下限为26 mm，上限为32.9 mm。测得的数据中轮缘厚度分布区间为27.5～31.3 mm，主要集中在28～ 30.5 mm 区间，如图1 所示。

图1 CRH2A 型动车轮对轮缘厚度分布

每间隔5 天轮缘厚度磨耗率VSd的计算公式为：

式中，ti+1和ti表示测量出该轮缘厚度数据的日期，ti+1−ti表示相隔的天数；Sdi+1和Sdi分别为不包含镟轮情况下ti+1和ti日期的轮缘厚度测量值。

将轮缘厚度和轮缘厚度磨耗率的计算数据进行拟合，结果如图2 所示。

但是，它们发生时并未丧失固有的本性，而依据这个本性，它们在发生之前，依然有不发生的可能性。“既然它各方面之所以具有必然性，是因为有神的知识这个条件，那它本身不具备必然性又有什么关系呢？”神意预知的事物必将发生，“只是其中有些东西是事物必然性的结果，有些东西是行事者努力的结果。”神意预知和自由意志的共融在这里得到完全的确证。

纵坐标为每5 天的轮缘磨耗率，横坐标为27.5～33.1 mm 范围内，每间隔0.1 mm 的轮缘厚度。拟合结果中，ESSE=0.025 87，ERMSE=0.021 89。SSE 和RMSE 值越接近0，说明该拟合结果解释数据的能力越强。

2.2 轮径磨耗建模

根据CRH2A 型动车组 2017 — 2019 年的数据，统计出每间隔30 天轮径的磨耗量，数据表明该动车每30 天的轮径磨耗量基本处于区间（−2 mm，5 mm）中。将磨耗量以间隔0.5 mm 划分为15 个区间，得到图3 所示的统计直方图。从图中可以看出，磨耗区间（0.5 mm，1 mm）和（1 mm，1.5 mm）所占的频数最高，轮径月磨耗量以1 mm 为中心，向两侧延伸，频数呈逐渐减小的趋势。

为得出该统计适合哪种分布，文本使用Matlab作为拟合工具，先后采用了Logistic 分布、正态分布、Gamma 分布、Weibull 分布进行拟合，拟合参数和结果如图4 所示。

Logistic 分布概率密度函数为：

式中，σ=0.787 ;µ=0.901。

正态分布概率密度函数为：

式中，σ=1.361 ;µ=0.9291。

图3 轮径月磨耗量统计直方图

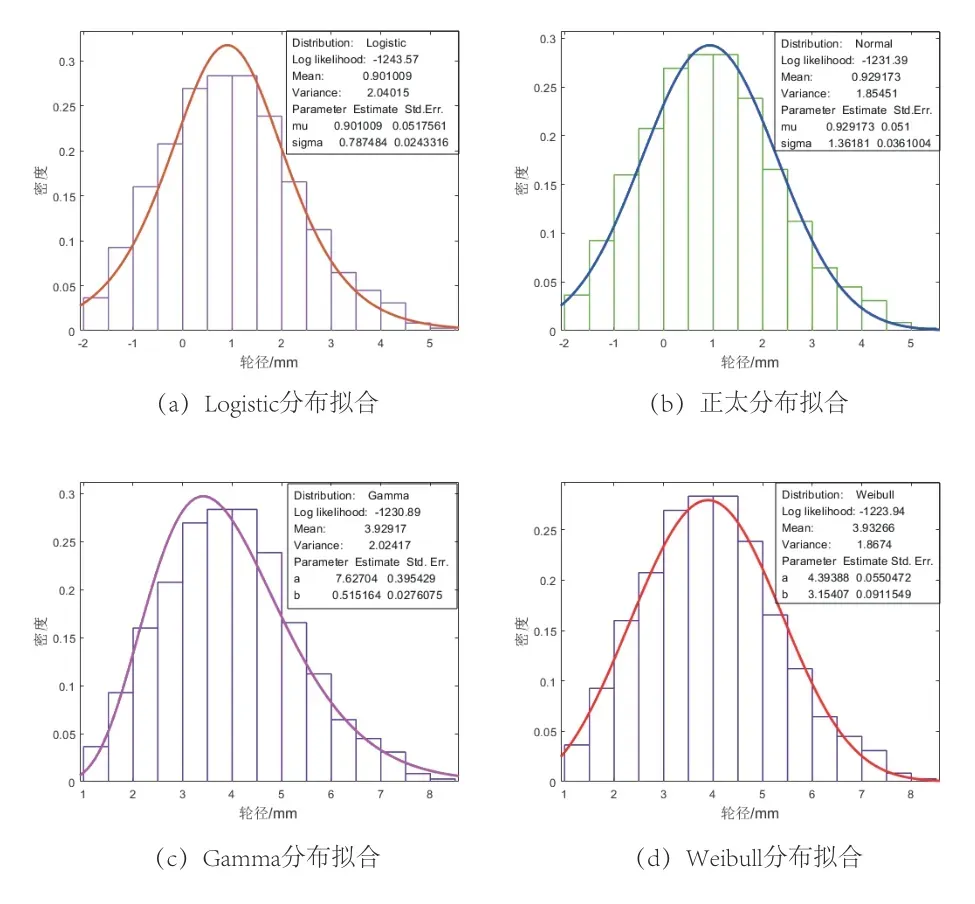
图4 4 种分布拟合的参数和结果

Gamma 分布概率密度函数为：

Weibull 分布概率密度函数为：

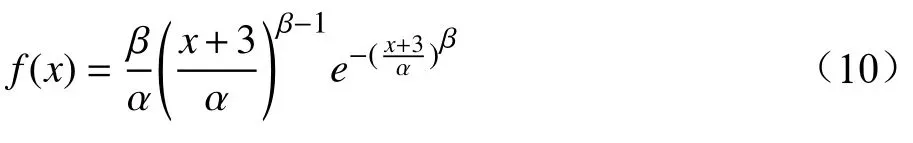
式中，α=4.393 ;β=3.154。

4 种分布拟合与实际数据统计直方图的对比如图5 所示。

图5 4 种分布拟合与实际数据对比

图中，Logistic 分布在高频部分存在错峰描述的误差；正态分布对高频和低频的统计都比较契合；Gamma 分布对高频部分的描述存在错峰的误差；Weibull 分布拟合整体比原数据偏低。结合表1 的卡方拟合优度检验（X2）来对比，Logistic 分布和Gamma 分布的X2值明显高于Weibull 分布和正态分布，表明预测结果与实际值相差较大，因此舍弃使用Logistic 分布和Gamma 分布。计算轮径月磨耗量位于0～ 5 mm 的概率，Weibull 分布和正态分布分别为0.723 和0.781。综上，本文选用正态分布作为轮径的统计模型。

2.3 镟修策略蒙特卡罗仿真

本文在建立轮缘厚度磨耗模型和轮径数理统计模型基础上，基于Matlab，采用蒙特卡罗方法仿真动车轮对在运行中的实际情况，并得到对应的镟修策略结果。设轮缘厚度的上、下限分别为SH 和SL，每一对车轮的轮缘厚度上下限可仿真出一组镟修方案，及相应的生命周期和镟修次数。将CRH2A 轮缘厚度的上下限区间 (26 mm,32.9 mm) 以0.3 mm为间隔取值，从而得到上下限组合。为避免出现上限太低的无意义镟修方案，本文上限取值区间为(29.9 mm,32.9 mm)，下限取值区间为 (26 mm,29 mm)，总计可以得到121 种镟修策略，仿真流程如图6 所示。

（1）设定仿真初始化参数，轮径的上限值D(0)=860 mm，轮缘厚度S d(0)=32.9 mm，两次镟修的间隔时间t=0，使用寿命T=0，镟修次数N=0。此处分别导入121 组镟修策略的上下限；

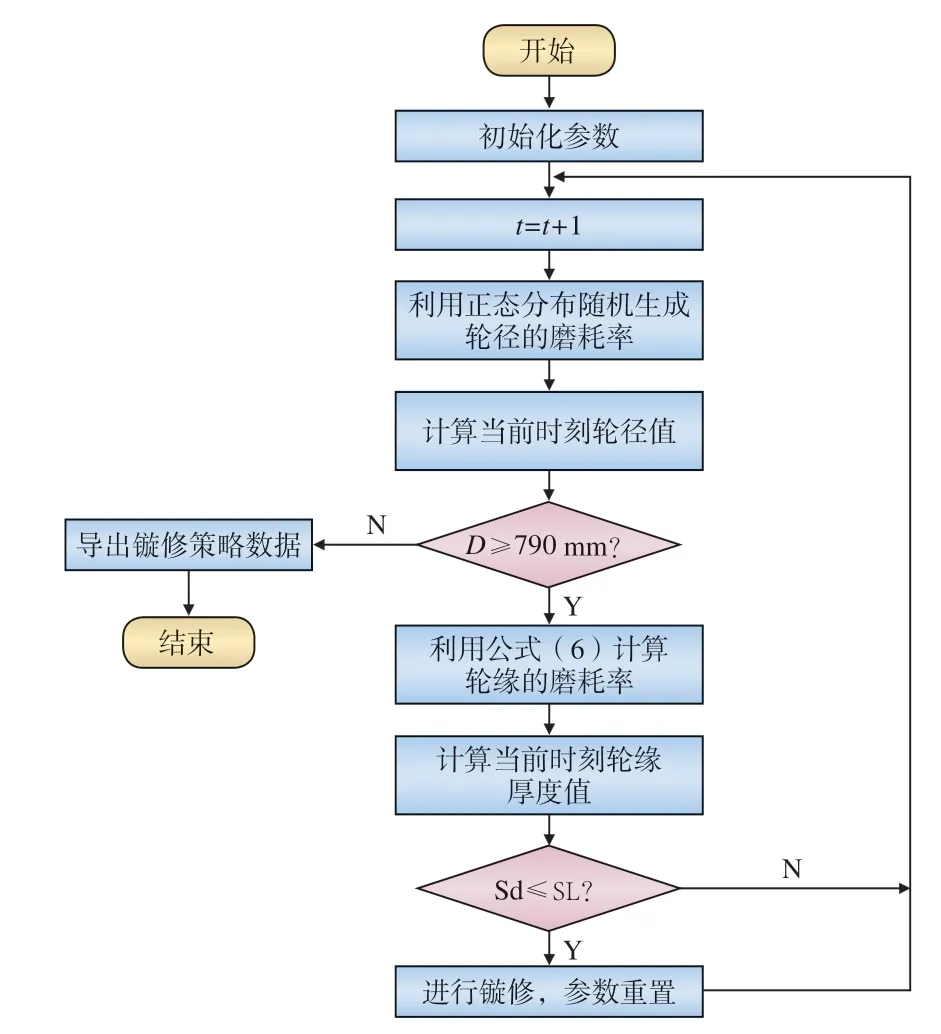
图6 蒙特卡罗仿真流程

（2）累计该组镟修策略的生命周期t=t+1；

（3）根据轮缘厚度的模型计算出轮缘厚度一个月的磨耗量ΔS d，从而得到当前轮缘厚度值S d(T+t+1)=S d(T+t)−ΔS d；同时，根据轮径的数理统计模型，生成当月的轮径磨耗量，得到磨耗一个月之后的轮径值D(T+t+1)=D(T+t)−ΔD；

（4）将当前轮径值D(T+t+1)与轮径下限790 mm 比较，如果低于790 mm，输出一组镟修策略的结果，镟修策略的生命周期Tend=T+t，镟修次数Nend=N；如果高于790 mm，判断轮缘厚度当前值S d(T+t+1)是否低于 SL，如果S d(T+t+1) 高于 SL，回到循环继续仿真；

（5）如果S d(T+t+1)低于SL，在此处进行一次镟修，根据镟修比例系数减少轮径值：D(T+t)=D(T+t+1)−k(S H−S L)，镟修次数N=N+1。将本次镟修之前的轮对时间存储起来T=T+t，并且重置参数：t=0,S d(T+t)=SH。

以当前采用的固定镟修模式作为对照，从所有的镟修策略中，选出最优的4 组方案 。根据目前列车运行和镟修动作的经济成本，对比得到最优的镟修策略。

图7 仿真结果

3 实验结果

本文仿真结果如图7 所示，121 种镟修策略的镟修次数集中在10 次上下，轮对的预期使用寿命集中在65～ 70 个月。目前，单轮镟修一次的成本XN为300 元，更换单轮的成本D为80 000 元，每月的单轮运行成本为

通过计算和对比，选出4 组较优策略。如表2所示，第1 行为当前镟修策略，其余4 行为仿真得出的4 组较优策略，其中，镟修组合（28.1，31.7）是月经济成本最低的一组，轮对的生命周期也最长，因此是经济效果最好的。

表2 镟修策略对比

4 结束语

本文基于轮对磨耗数据，研究了一种能提高CRH2A型动车轮对生命周期的镟修策略。在动车轮对两个重要数据轮径和轮缘厚度中寻找规律并建立模型，采用蒙特卡罗仿真方法，得出CRH2A 型动车组采用不同镟修策略的实际经济效果。结果表明，通过仿真得到的镟修策略中存在生命周期更长，镟修次数更合理的方案。相较于目前的镟修策略，动车轮对运营的经济性得到提高。采用经济成本衡量的方式，可直观得出不同镟修策略的优劣，以便做出更好的决策。