民用涡轴发动机动力涡轮盘破裂转速研究
聂卫健,邓旺群,皮滋滋,卢 波,刘文魁
(1.中国航发湖南动力机械研究所,湖南株洲 412002;2.中国航空发动机集团航空发动机振动技术重点实验室,湖南株洲 412002)
1 引言
民用航空发动机的轮盘设计必须保证轮盘的结构完整性并具有一定的强度储备。由于轮盘的破裂是非包容性的,轮盘一旦发生破裂,碎片打穿机匣后,可能损坏油路系统和操作系统,造成严重后果,因此对轮盘破裂转速进行研究具有十分重要的意义。国外学者对轮盘破裂转速的研究较早,并在应力分析和破裂转速预测方面取得一定成果[1-3]。国内在破裂转速预测与破裂失效模式方面[4-5]进行了相关研究,选用的预测轮盘破裂转速的准则主要有平均应力准则、大变形法及最大周向(径向)应力准则、第一主应力和等效应力准则等[6]。如吴长波等[7]采用传统平均应力法预测了高压涡轮整体叶盘的破裂转速;万江艳等[8]建立了轮盘弹塑性盘破裂准则,并对变厚度轮盘破裂转速进行了预测;冯引利等[9-10]分别对粉末冶金高温合金涡轮盘破裂转速和轮盘径向破裂转速进行了分析,提出了基于有限元的破裂转速计算修正方法;秦仕勇等[11]对粉末冶金涡轮盘进行了改进,并进行了破裂转速分析和试验验证;古爱军等[12]针对轴流式轮盘的破裂转速,提出一种应用有限元法计算轮盘破裂转速的破裂准则。
本文采用平均应力法及弹塑性有限元法,分别对某民用涡轴发动机动力涡轮盘进行了破裂转速分析;通过破裂转速测量试验,获取了动力涡轮一级盘和动力涡轮二级盘的破裂转速和破裂形式,并与计算结果进行了对比分析。研究可为动力涡轮盘优化设计及同类型轮盘破裂转速分析与试验提供借鉴和参考。
2 破裂转速分析
2.1 有限元模型
运用ANSYS 有限元分析软件对动力涡轮盘进行有限元网格划分和建模。采用十节点四面体单元对动力涡轮盘进行网格划分。由于动力涡轮一级盘包含50个榫槽和14个安装孔,动力涡轮二级盘包含50个榫槽,因此,为减小计算工作量,取动力涡轮一级盘的1/14循环对称段(包含一个安装孔在内)和动力涡轮二级盘的1/50 循环对称段作为计算模型(不影响计算结果)。建模时,离心载荷和温度载荷分别以转速形式、节点温度形式施加在模型上,同时约束A面的轴向位移和周向位移,并在切割面上施加循环对称约束。动力涡轮一级盘和动力涡轮二级盘的有限元模型分别见图1、图2。

图1 动力涡轮一级盘有限元模型Fig.1 Finite element model of the first stage disk of power turbine

图2 动力涡轮二级盘有限元模型Fig.2 Finite element model of the second stage disk of power turbine
2.2 平均应力法分析
平均应力法[13]认为,当轮盘任一半径处的径向平均应力达到材料的单向拉伸强度时,轮盘在该半径处沿圆柱面破裂;当轮盘的周向平均应力达到材料的单向拉伸强度时,轮盘沿子午面破裂。圆柱面破裂和子午面破裂转速平均应力法计算表达式分别如式(1)、式(2)所示。


采用平均应力法分别对动力涡轮一级盘和动力涡轮二级盘子午截面、圆柱截面破裂转速进行分析。动力涡轮一级盘和动力涡轮二级盘的应力分布云图见图3、图4,计算得到的破裂转速见表1。从表中可知,动力涡轮一级盘和动力涡轮二级盘子午截面破裂转速均比圆柱截面破裂转速低。由此可以推断,动力涡轮一级盘和动力涡轮二级盘的破裂形式均为子午面破裂。

表1 动力涡轮盘破裂转速计算结果(基于平均应力法)Table 1 Calculation results of the rupture speed(based on mean stress method)

图3 动力涡轮一级盘应力分布图Fig.3 Stress distribution diagram of the first stage disk of power turbine
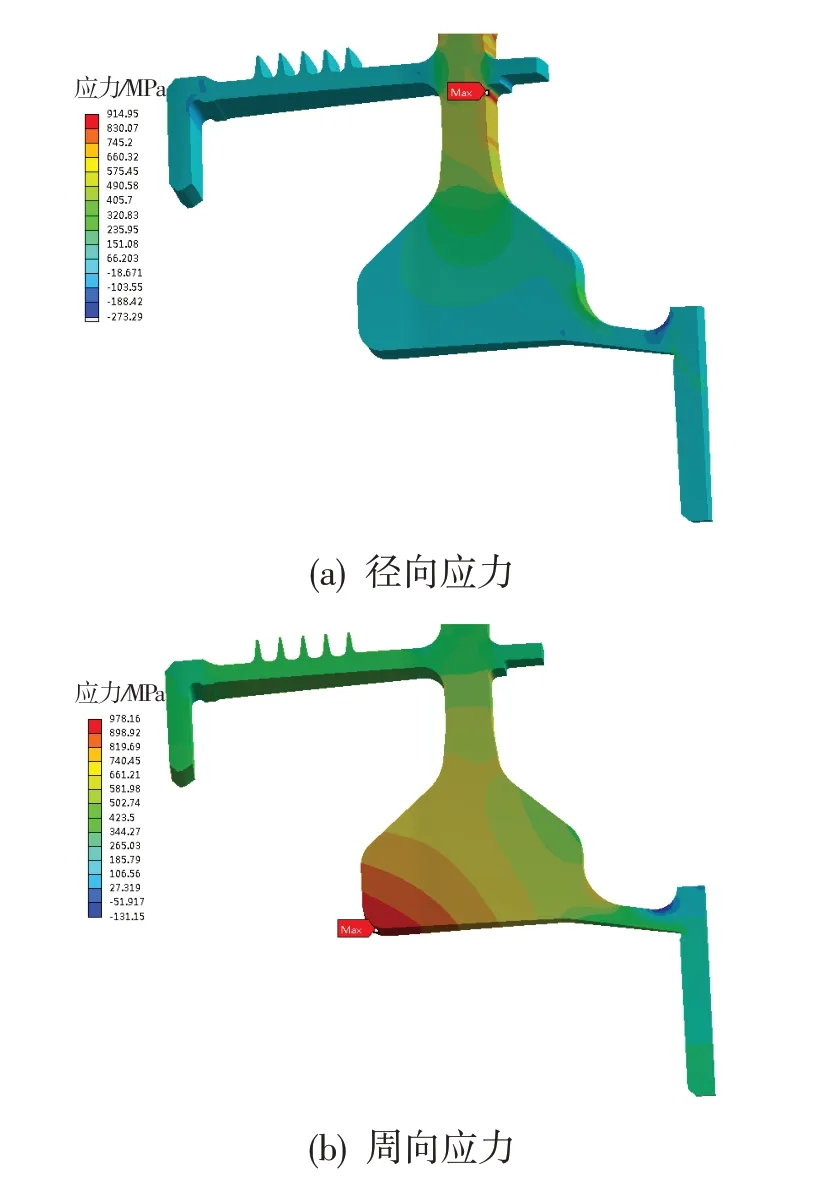
图4 动力涡轮二级盘应力分布图Fig.4 Stress distribution diagram of the second stage disk of power turbine
2.3 弹塑性有限元法分析
采取弹塑性有限元法对动力涡轮一级盘和动力涡轮二级盘破裂转速进行计算分析。动力涡轮一级盘和动力涡轮二级盘的应变分布分别见图5、图6,计算得到的破裂转速见表2。

表2 动力涡轮盘破裂转速计算结果(基于弹塑性有限元法)Table 2 Calculation results of the rupture speed(based on elastic-plastic finite element method)
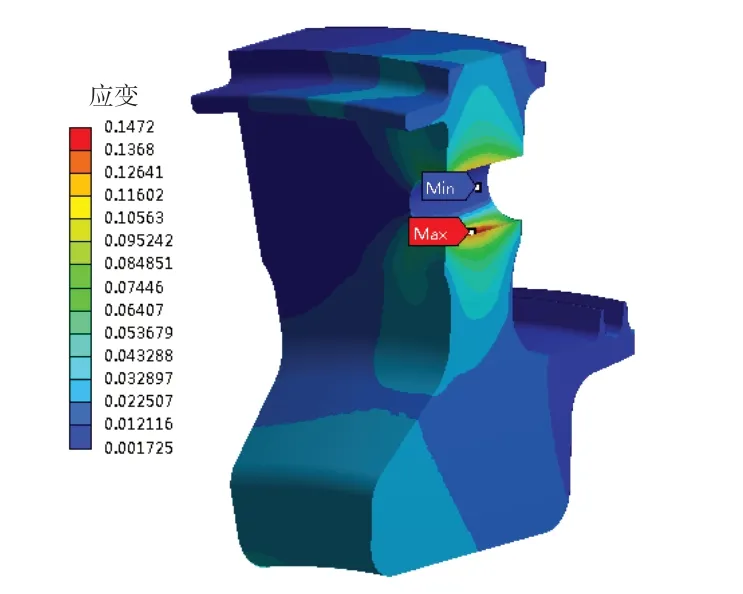
图5 动力涡轮一级盘应变分布云图Fig.5 Strain distribution diagram of the first stage disk of power turbine

图6 动力涡轮二级盘应变分布云图Fig.6 Strain distribution diagram of the second stage disk of power turbine
3 强度计算与校核
动力涡轮一级盘、动力涡轮二级盘与试验工装和配重叶片的装配示意图分别见图7、图8。

图7 动力涡轮一级盘装配示意图Fig.7 Assembly diagram of the first stage power turbine disk

图8 动力涡轮二级盘装配示意图Fig.8 Assembly diagram of the second stage power turbine disk
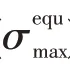

表3 试验工装强度校核结果Table 3 Intensity check results of test fixtures

表4 叶身强度校核结果Table 4 Intensity check results of blades

表5 榫头强度校核结果Table 5 Intensity check results of blade dovetail
4 破裂转速测量试验
4.1 试验温度标定
试验在均匀温度场下进行。为保证温度均匀和温度控制、温度测试的准确性,在试验前对试验温度进行了标定。标定时,在试验件附近布置温控和监控热电偶,在轮盘上几个位置布置一定数量的热电偶(T1~T4),测量温度。按梯度进行升温,并在试验温度下保温一定时间,以确保试验温度均匀。动力涡轮一级盘和动力涡轮二级盘温度标定热电偶分布示意图及照片分别见图9、图10,温度标定结果见表6。可见:动力涡轮一级盘温度与动力涡轮二级盘温度标定误差均在±5℃内,满足试验器温度控制精度要求;经过升温和保温过程后,加温炉内温度已达到试验所需温度并保持均匀状态。

表6 试验温度标定结果Table 6 Temperature calibration results

图9 动力涡轮一级盘温度标定示意图及现场照片Fig.9 Temperature calibration diagram and photo of the first stage power turbine disk

图10 动力涡轮二级盘温度标定示意图及现场照片Fig.10 Temperature calibration diagram and photo of the second stage power turbine disk
4.2 试验过程
试验在立式轮盘试验器上进行。安装试验件和加热炉后,按温度标定时位置布置温控热电偶和监控热电偶,关闭试验舱盖并抽真空,进行升温(升温过程与温度标定时的一致)并保温。试验时,转速按阶梯上升,在特征转速下停留一定时间后继续上升,直至轮盘破裂。试验过程中测得的转速、振动位移随时间的变化曲线分别见图11、图12。可见,动力涡轮一级盘和动力涡轮二级盘破裂时,振动位移突变,试验器自动保护停车,由此得到动力涡轮一级盘和动力涡轮二级盘的破裂转速分别为34 339 r/min、33 233 r/min。

图11 动力涡轮一级盘转速与振动位移随时间的变化曲线Fig.11 Curve of speed and vibration vs.time for the first stage disk of power turbine

图12 动力涡轮二级盘转速与振动位移随时间的变化曲线Fig.12 Curve of speed and vibration vs.time for the second stage disk of power turbine
4.3 试验结果及分析
试验后,试验工装基本完好,动力涡轮一级盘破裂成4大块,动力涡轮二级盘破裂成3大块,为典型的子午面破裂形式,验证了2.2节中计算结果的正确性。试验工装及试验件残骸照片见图13、图14。

图13 动力涡轮一级盘破裂后残骸照片Fig.13 Wreckage picture of the first stage power turbine disk and fixture after rupture

图14 动力涡轮二级盘破裂后照片Fig.14 Wreckage picture of the second stage power turbine disk and fixture after rupture
表7给出了动力涡轮一级盘和动力涡轮二级盘破裂转速计算误差。表中,计算误差根据公式(3)计算。从表中可知,与试验结果相比,平均应力法和弹塑性有限元计算得到的破裂转速均偏小,平均应力法计算误差不大于12.59%,弹塑性有限元法计算误差不大于6.72%。总体看,弹塑性有限元法计算误差较小,与试验结果较吻合。

表7 动力涡轮盘破裂转速计算误差Table 7 The calculation errors of the rupture speed

5 结论
以民用涡轴发动机的动力涡轮一级盘和动力涡轮二级盘为研究对象,对其进行了破裂转速研究和试验验证,主要结论如下:
(1) 动力涡轮一级盘和动力涡轮二级盘的破裂形式均为子午面破裂。
(2) 平均应力法计算误差相对较大,弹塑性有限元法计算结果与试验结果吻合较好。
(3) 轮盘破裂后,试验工装基本完好,工装结构设计和强度满足试验要求,强度校核方法可行。

