面向发动机喷管测量的多目拼接算法

孙延鹏，常占友，陈新禹，王 鹏

(1.沈阳航空航天大学，沈阳 110136；2.中国航发四川燃气涡轮研究院，成都 610500)

1 引言

立体视觉测量方法具有非接触性、效率高和精度高等优点[1]，能够应用于航空发动机喷管的测量。然而，发动机喷管尺寸较大，采用双目立体视觉测量，存在测量范围受限问题，难以完成对整个喷管几何尺寸的测量；采用多目视觉测量可实现对整个喷管的测量，但面临多个双目测量单元间的数据拼接难题[2-3]。

目前，多目拼接算法主要分为以下两种：一是基于精密仪器的辅助测量方法。一般采用经纬仪[4]、全站仪[5]、激光跟踪仪[6]等精密设备实现非接触测量，但这些设备存在操作复杂、价格昂贵、灵活性差等不足。二是直接求取转换矩阵的方法。杨超[7]通过实验仿真发现，在三维数据拼接方面，奇异值分解(SVD)法比三点法、单位四元素法具有更大的优势。何航[8]提出了基于平面靶标的数据拼接方法，通过靶标上的非共线标记点将相邻局部坐标系的三维数据统一到同一坐标系下，但这种方法存在误差累积的问题。金露[9]采用线性加权法和循环拼接法来降低三维数据拼接的累积误差，不需要标记辅助点，避免了利用转台进行拼接时出现的定心不准问题，但是没有对如何求解拼接矩阵问题进行研究和实验仿真。杜娜等[10]提出一种针对多目立体视觉坐标测量技术的拼接算法，仅求解线性方程就能处理公共点面的三维数据拼接，但是求解转换矩阵时用多次求解出来的转换矩阵求平均会增加拼接误差，给实验结果带来较大偏差。总之，对于发动机喷管运动过程中的实时测量还没有全面、实用的相关研究，且对于三维数据拼接算法研究成果较少。

本文针对现有拼接算法进行分析，在双目立体视觉单元的基础上(双目视觉单元下能够获取三维坐标点)，针对多双目立体视觉单元间的三维数据进行拼接(可应用三维数据拼接方法实现拼接)，提出一种随机法和穷举法相结合的拼接算法。其主要设计思路是：对于三维数据点的个数进行选择。对于10个以上的三维数据点采用随机法，对于10个以内的三维数据点采用穷举法，利用求解的局部转移矩阵将不同视点下的数据拼接到一个坐标系下。

2 多目拼接系统

2.1 多目拼接原理

多目拼接是将不同视点下的观测数据融合到统一视点下，同时弥补双目在测量上存在的不足，能够更好地研究和测量发动机喷管的动态位姿和运动参数[1-2]。对于矢量喷管，由于其只存在旋转和平移的刚体运动，所以多目拼接的关键是求出两视点的转化矩阵。

三维数据拼接的前提是不同视点下存在若干个公共点，当每个视点存在3个或3个以上的非共线公共点时，将多个视点下的公共点数据通过转换矩阵融合到同一坐标系，便可实现多视点数据拼接。

2.2 多目拼接算法设计

由于本文研究的发动机矢量喷管的运动过程是一种刚体运动，所以多视拼接的关键就是求解出视点间的转换矩阵，然后将不同视点下的数据通过转换矩阵都融合到一个视点下完成拼接。求解转换矩阵的方法有SVD 法、最小二乘法、七参数法等。理论上公共点越多，解出来的转换矩阵越准确，实现多目拼接的精度越高。然而在实际测量过程中，受测量误差和噪声等影响，多目拼接的精度并不高。理论上本文算法对于多视点下3个及3个以上的非共线公共点都可以实现很好的拼接，但随着公共点的增加，迭代次数和误差也会增加。考虑到此种情况，下面以视点下不超过10 个公共点为例。设计的算法描述如下：

第1 步，确定公共点的个数n。假设存在视点B和视点A两个不同视点，且两个视点下存在n(3 ≤n ≤10)个公共点，并求出从n中随机取3个公共点的组合。

第2 步，求解转换矩阵M。首先以第一步选取的任意3个公共点为例，使用文献[10]方法引入1个辅助点，使得成为4 个公共点。假设组成的新的两对应矩阵分别为P 和Q，则P 和Q存在相应的变换关系，可表示为式(1)。

第3 步，算法选择。如果n＞5，则选择随机法，否则选择穷举法。

第4 步，穷举法算法设计。为求解使得多视拼接精度最高的M，用穷举法求解第1 步所有可能组合的转换矩阵，选出使得拼接误差最小的M，并求解出最小均方误差。

第5步，随机法算法设计。若n＞5，则两视点的非共线公共点数较多，直接用穷举法会增加算法的计算量，降低算法的效率，为此应采用随机法的算法。从n个公共点中随机选取3个非共线的公共点，求解M；重复n次，选择使拼接误差较小的最优M，并求解出最小均方误差。

多目拼接的算法流程图如图1所示。

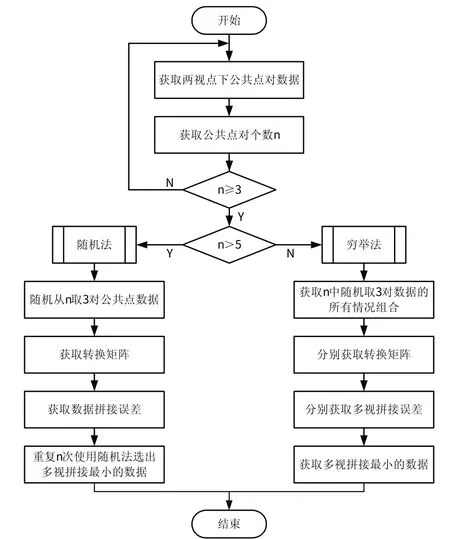
图1 多目拼接的算法流程图Fig.1 The flow chart of multi-view splicing algorithm

考虑到以最小均方误差进行判断，有可能选择的点非常集中，不利于计算。为此，本文也考虑点的分布比较集中的情况，对本文算法进行自验证，使得选取的数据点更合理、更具有说服力。下面对自验证算法设计进行说明：首先计算对应视点下每两个点组成的边的均方误差error，然后计算对应视点下每两个点组成的边的均方误差，再进行判断。若error＞精度值，重新选择矩阵B 和A(分别对应视点B和视点A下数据)，找到满足精度值要求的误差最小的点；若error≤精度值，则保留这3 个点作为要实现多目拼接的点，并重复前5 步操作。自验证算法流程图如图2所示。

图2 自验证算法流程图Fig.2 T he flow chart of self-verification algorithm

2.3 欧拉角计算

为降低算法的复杂度及更好地估计矢量喷管的姿态，将求出的转换矩阵转换为欧拉角表示。通过已求出的转换矩阵求解旋转矩阵R(9个参数)，进而求出欧拉角(3个参数)，从而降低算法的复杂度。旋转矩阵可表示为：

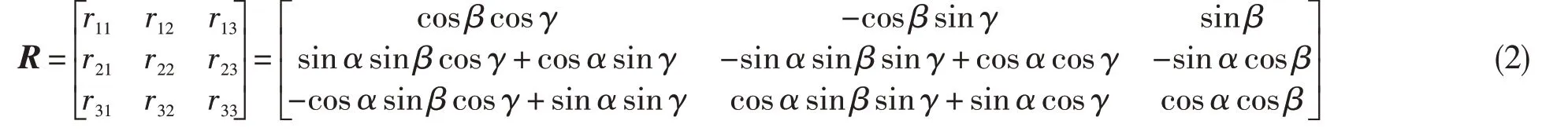
绕X轴欧拉角可表示为：

绕Y轴欧拉角可表示为：

绕Z轴欧拉角可表示为：

3 实验验证

3.1 数据拼接实验数据

矢量喷管喷口(静态状况下喷口边沿视为圆形)在偏转时会形成各种空间位姿，下面仅对喷口的几何形状进行仿真。仿真了半径为153.85 cm、圆心为(-74.89 cm，-43.93 cm，2049.72 cm)的空间圆，其中实验仿真效果如图3所示。对多目数据拼接实验的条件进行描述：在空间圆上随机选取19个坐标点作为视点B下的数据，如图3中蓝点所示；原始视点A下的16个三维数据点如图3中红点所示。下面提供基于外参数数据拼接的实验测试仿真数据。表1为原始视点B和A下的三维数据，表2 为原始两视点下的公共点数据。

表1 原始视点B和A下的三维数据Table 1 3D data of original viewpoint B and A 3D data

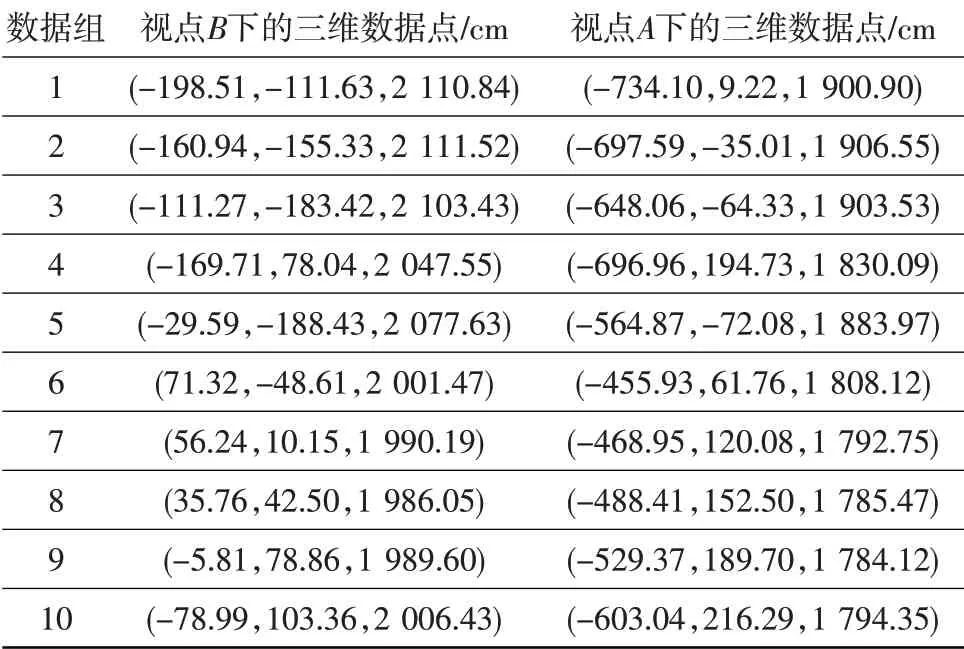
表2 原始两视点下的公共点数据Table 2 Common point data under the original two viewpoints

图3 矢量喷管喷口模拟效果图Fig.3 The diagram of vector nozzle simulation effect

为使得数据更可靠，在视点A下的数据中加入均值为0、方差为0.1 的噪声，对视点数据拼接进行模拟实验，完成多目视觉测量实验模拟仿真。应用本文提出的算法求解最优转换矩阵，并求出算法的最小均方误差。

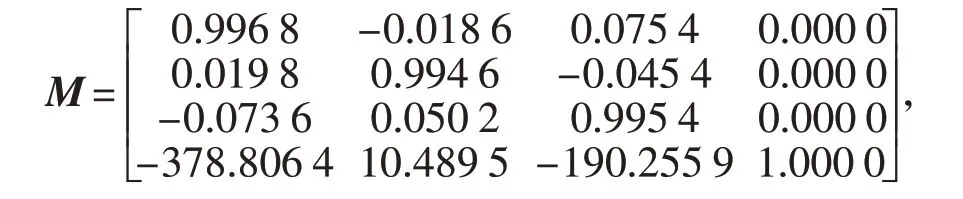
最小均方误差为1.04×10-14。可见本文算法精度较高，能很好地用于多视点数据拼接，从而能够更好地研究和测量发动机喷管三维运动场景。

为更好地验证实验的合理性，对求解出的转换矩阵进行验证。主要内容如下：假设选出的不同视点下最优的3个非共线公共点分别为数据C和数据D，对比分析视点C通过转换矩阵得到的数据E与数据D，以数据E中三维点连线构成的三角形与数据D中构成的三角形满足全等作为约束，验证选出的公共点是否正确，从而更好地验证算法的合理性。根据本文算法选出的两对应视点下的3个非共线公共点，与原始实验数据进行对比，验证本文算法的合理性。其中仿真求解出的最优的3个非共线公共点如表3所示。

表3 选出的最优3个非共线公共点Table 3 Optimal 3 non-collinear common points selected

为进一步验证本文算法的合理性，对比本文算法与最小二乘法和文献[7]、文献[10]中算法实现表2数据拼接实验的最小均方误差，结果如表4所示。

表4 几种数据拼接算法的最小均方误差Table 4 Least mean square error data of several data splicing algorithms

3.2 数据拼接实验仿真效果

应用本文算法进行数据仿真。具体介绍如下：本次数据来源同表1中数据，并将图3作为原始仿真效果。选出最优的3 个非共线公共点实现多视拼接，结果如图4 所示，其中绿色数据为视点B下的数据经过转换矩阵变换后的数据。

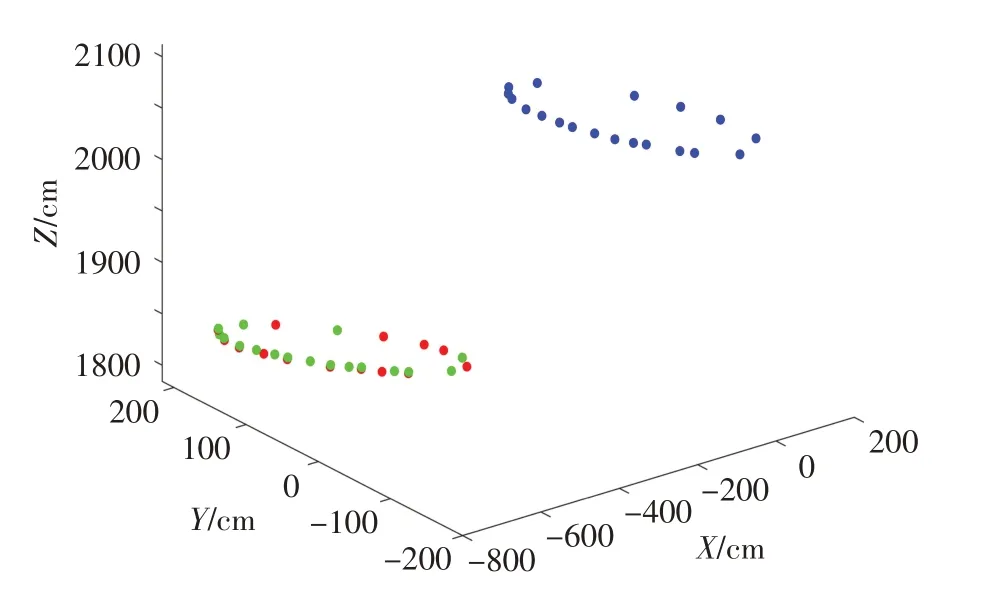
图4 选出最优的3个非共线公共点实现多视拼接的仿真图Fig.4 Simulation of selecting the optimal 3 non-common-line common points for multi-view stitching

为测试算法的可靠性，重复14次表1中数据，并在视点A下的数据中加入均值为0、方差为0.1 的噪声，拟合拟合圆的半径和原始仿真圆的半径进行数据对比，结果如表5所示。由表可知，拟合数据与真实数据之间的最大半径误差为0.08 cm，最小半径误差为0.00 cm，半径误差平均值为0.03 cm。结合图4多目拼接效果可知，应用本文算法可以将视点B下数据很好地拼接到视点A下，表明本文算法具有较高的测量精度。

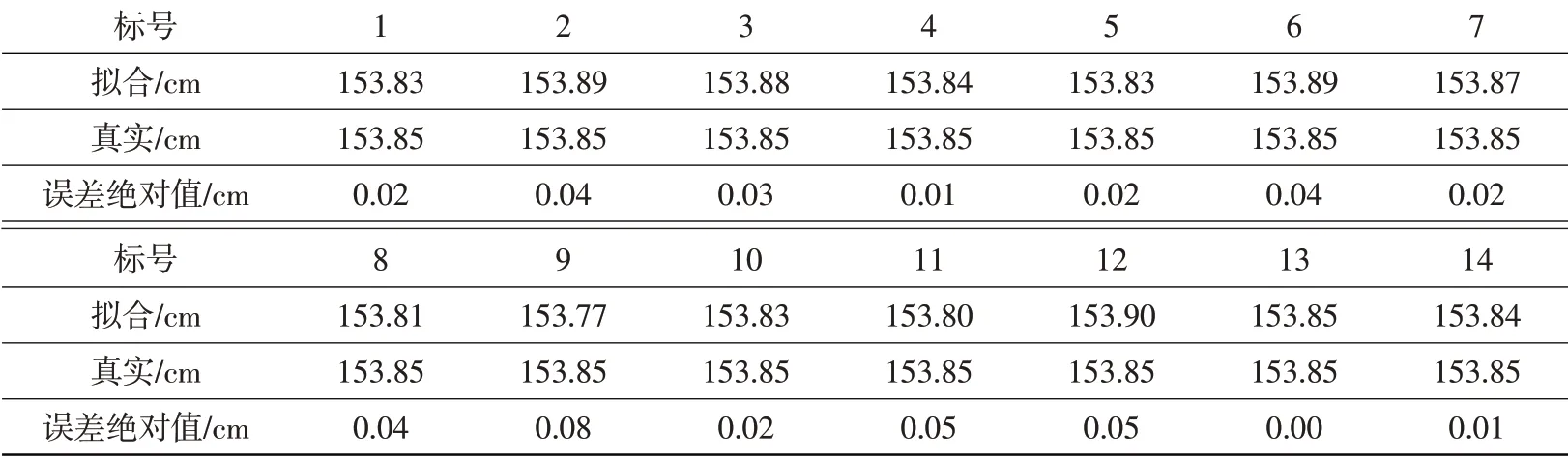
表5 拟合数据半径与真实数据半径对比Table 5 Comparison between fitting data radius and real data radius

3.3 欧拉角实验

在计算机视觉研究中，对于求出的用9 个参数表示的旋转矩阵，通常需要转换为3 参数的欧拉角表示，这样可以减少算法的复杂度。应用式(3)～式(5)，可直接通过旋转矩阵求解欧拉角。

为研究矢量喷管喷口在偏转时形成的各种空间位姿，以便测量喷口边沿形成的欧拉角参数，需要将求解出来的旋转矩阵转为欧拉角表示，从而为研究矢量喷管喷口对发动机推力影响提供理论设计和实验数据。以式(3)中求得的最优旋转矩阵为例，欧拉角实验测试数据如表6。

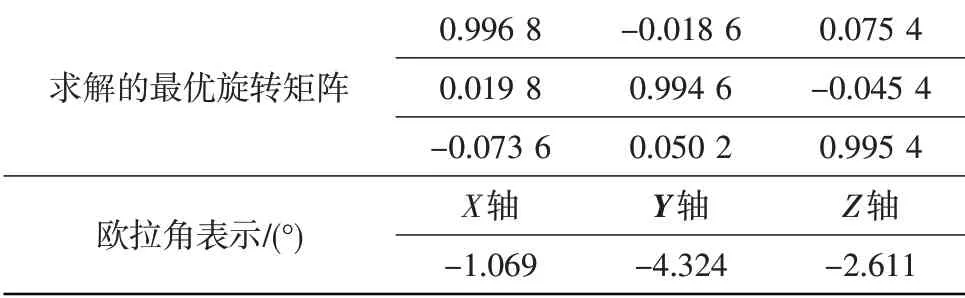
表6 欧拉角实验测试数据Table 6 Euler angle experiment data

4 结论

针对现有拼接算法进行分析，在双目立体视觉单元的基础上，针对多双目立体视觉单元间的三维数据进行拼接，提出一种随机法和穷举法相结合的拼接算法。给出了具体的算法设计流程，并用拟合圆和真实圆之间半径绝对误差作为评价指标，数据拼接误差平均值为0.03 cm。视觉拼接实验也表明，本文提出的拼接算法具有较高的测量精度。此外，本文将求解的旋转矩阵转换为欧拉角，降低了算法的复杂度。现阶段仅对算法进行了理论上的推导和实验仿真，接下来将搭建多目立体视觉环境对真实矢量喷管进行测量，进一步研究本文算法的拼接误差和拼接效果。