支板喷射超燃冲压发动机激波/边界层相互作用研究

王力军，范荆鹏，徐义俊，门 阔

(沈阳航空航天大学能源与环境学院，沈阳 110136)

1 引言

高超声速推进器中普遍存在激波/边界层干扰(SBLI)现象，并由此引发一系列严重影响其性能的问题，如流动分离、总压损失、气动热力效应等[1-3]。Ferry[4]首次在超声速风洞中观察到SBLI产生的流动分离现象，随后学术界对这一现象展开了大量研究。研究表明，SBLI和流动分离现象会对高超声速推进器产生较大的气动热载荷[1]，并且激波/边界层相互作用将导致壁面处的压力和传热产生波动，增加气体黏性耗散，导致流道内阻力上升[5]。同时，流道内激波的存在也增加了气体的流动损失[6]。理论上，气流总压损失是衡量高超声速推进器性能的重要参数，而流道中SBLI 现象会造成一定的总压损失，导致推进器性能下降[7]。因此，有必要深入研究超声速流动过程中的SBLI现象。

支板喷射超燃冲压发动机由于将燃料直接喷射入主流中获得了良好的混合效果，同时其支板结构还具有稳定火焰的作用，但高超声速流动中引入支板结构必然会产生激波、膨胀波，并由此导致SBLI、流动分离现象及流动损失。为此，日本宇航局(NAL)进行了大量的地面实验，获取的实验数据已成为数值模拟CFD 的佐证[8-10]。不少研究也是基于上述实验，从不同方面探究了支板喷射超燃冲压发动机的流动特性[11]、燃料混合以及燃烧流动特性等[12-13]。已有试验证明，明渠流动可以在一定条件下模拟超声速流动，且试验设备相对简单，流动现象更易观察[14-15]。本文选取日、法合作的CNR11-R36支板喷射超燃冲压发动机为研究对象，在实验模化的基础上，利用Fluent®商业软件，对其内部流场的SBLI、流动分离现象及流动损失等高超声速的复杂流动进行数值模拟与分析，研究结果对超声速飞行器的研制及性能优化具有重要意义。

2 模化实验与模拟条件

2.1 实验模型

图1 为超燃冲压发动机燃烧室的实验模型图。燃烧室等直段长度L1为355.0 mm，扩张段长度L2为600.0 mm。支板高度H为10.0 mm，宽度为11.5 mm，尾部斜面角36.0°，壁面厚度均为1.0 mm，安装在燃烧室的喉部。支板尾部等间距布置6个直径为3.5 mm的燃料喷孔。入口截面为50.0 mm×100.0 mm，出口截面为86.0 mm×100.0 mm。

图1 超燃冲压发动机燃烧室实验模型Fig.1 Experimental model of scramjet engine combustor

2.2 实验原理和方法

超声速流与明渠流动的相似模化方法是在相似的边界条件下，用明渠流动的水跃波模化高超声速的流动波系，其相似原理见文献[16]。基于实验模型搭建的明渠流动模型见图2。用工业相机MV-GX150C 捕捉水流的瞬时波动过程。实验方法是在收缩-扩张明渠流道的喉部将水流提升为超临界流动，通过电磁流量计控制水流速度，从而模化不同条件的超燃冲压发动机燃烧室内的高超声速空气流动。

图2 明渠流动模型实验台Fig.2 Experimental platform of open-channel flow model

2.3 数值模拟方法及条件

数值模拟中的边界条件如表1 所示，表中Ma为飞行马赫数，TT为滞止温度，pT为滞止压力，h为实验水深。考虑到计算资源和计算结果的精确度，湍流模型采用k-ω SST 两方程湍流模型，其优点是增加了横向耗散导数项，适用于计算高超声速流动下的激波问题[17]。该湍流模型中，限制湍流剪切应力系数a1的默认条件不能准确预测逆压梯度下的分离。Nicholas[18]的研究发现，a1取0.355时数值模拟结果与实验结果一致，尤其是对于某些复杂流场的计算，因此本文a1取0.355。对流通量采用AUSM 格式，变量梯度采用Green-Gauss Node Based 格式，计算收敛精度为10-5。控制方程离散采用二阶迎风格式。

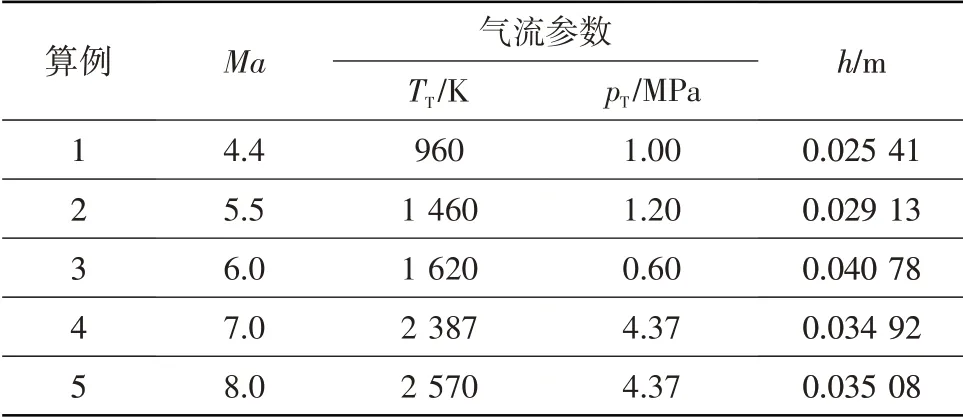
表1 测试模拟边界条件Table 1 Test simulated boundary conditions

2.4 网格划分

利用软件ICEM 对计算域进行网格划分，采用非结构化网格。壁面为5层棱柱边界层，y+≤5。图3 为网格无关性检验结果。可以看出，计算壁压与实验壁压存在一定差异，上游壁压更贴近实验值。这是由于流动过程存在激波干扰时，边界层分离在一定程度上增强了反射激波，造成反射激波前移，导致越靠近下游，压力峰值的计算值与实验值的偏差越大。分别选取198万、274万及351万网格进行无关性验证，得出采用351 万网格计算的壁面压力与文献[10]的实验值平均误差为4.14%，不超过5%，符合要求。据此，后续研究中网格数均取351万。

图3 不同网格数量对应的壁面压力分布Fig.3 The wall pressure distribution for different mesh numbers

3 结果分析

3.1 实验结果分析

图4为不同边界条件下对应明渠流动实验的水跃波系图。可见，水跃波产生于支板前缘，在向下游流动过程中，因受壁面限制，在流道与支板壁面之间产生多次反射。随着流速增加，支板尾缘的水跃波与水平方向的夹角α从28°逐渐减小至23°。

图4 明渠流动实验的水跃波系图Fig.4 The water leap wave system of the open-channel flow experiment

3.2 数值模拟结果分析

数值模拟结果中，膨胀波内压力较小会被流场掩盖无法显示，为此采用速度散度(∇·V)来描述流场内激波(∇·V＜0)、膨胀波(∇·V＞0)的变化。图5给出了算例1的流场数值模拟结果。由图5(a)、图5(b)可以看出，流动由等直段进入扩张段时，由于扩张角的存在，流道壁面X=355.0 mm 处产生了膨胀波，但因扩张角较小(1.72°)产生的膨胀波较弱，未能穿过支板前缘产生的弓形激波。弓形激波的存在导致气流减速增压，同时气流的密度和温度也有一定的增加。气流经过支板扩张段尾部(X=384.0 mm)时产生一道膨胀波，弓形激波到达流道上、下壁面时会产生反射激波，激波强度减弱，膨胀波与反射激波相交。由于膨胀波内压力较小，导致反射激波穿透时向燃烧室中心偏转，然后经支板壁面再次反射。随着流动的发展，气流经过支板尾缘(X=438.0 mm)时，由于流道面积突然扩大，在支板尾缘处形成一系列膨胀波。此时，膨胀波后气流压力下降，为平衡膨胀波后气流压力，燃料喷嘴处产生了两道斜激波。弓形激波经过壁面的不断反射，其强度不断减弱。多次反射后的激波穿过支板尾缘的膨胀波和斜激波时，其强度进一步减弱，反射激波逐渐消失。因此，燃烧室下游的波系结构由燃料喷嘴产生的斜激波及其在流道壁面间的反射激波所主导。

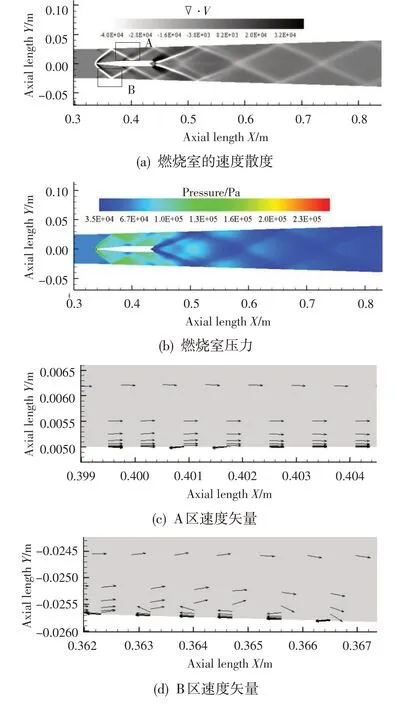
图5 算例1流场数值模拟结果Fig.5 Numerical simulation results of flow field for case 1

高超声速来流气体经过支板前缘钝头体产生一道弓形激波，由于支板前为等值段，流动未受干扰，理论上不存在流动损失，因此此处产生的弓形激波强度最高；此外，弓形激波发展至流道壁面处与壁面边界层产生强烈的相互作用导致此处边界层发生分离，如图5(c)(燃烧室中心截面，顺气流方向)所示。由图5(c)、图5(d)可见，当弓形激波及壁面反射激波入射到壁面层流边界层时，在气体黏性作用下，边界层内气流(层流流动)越靠近壁面流速越低，紧邻壁面流速近乎为0。由于激波在超声速流动中形成，因此激波从主流区射向壁面时只能延伸至边界层内声速位置，不能直接作用于壁面上；气流穿越激波后压力突跃上升，且波后气流压力升高不能逆超声速流动向上游传播影响激波前的流场，但却能通过边界层内亚声速区逆向前传，使激波入射点附近压力有所升高，因此此处流速降低，边界层增厚，流线凸起。同时在边界层上方形成强烈的逆压梯度，导致边界层分离。激波后的气流压力较高，激波穿过边界层亚声速区向上游移动，因此分离的边界层出现在激波作用点上游。同时，分离的边界层还会诱导产生分离激波，随后分离的边界层又会重新附着于壁面，重新附着过程中形成的再附激波与上述分离激波相交形成反射激波。

3.3 入口马赫数对SBLI及支板近壁流动的影响

激波/支板壁面边界层干扰区变化如图6 所示。从图中可以发现：①随着入口马赫数增加，流线凸起增大，分离区逐渐显现；②随着入口马赫数增加，激波/边界层干扰区逐渐向下游移动。出现上述现象的原因是：随着入口马赫数增加，激波角减小促使激波与边界层作用点向下游移动；激波前后压比增大，激波强度增加，激波在作用点垂直方向的逆压梯度增大，从而导致边界层增厚，流线凸起增大。此外，随着入口马赫数增加，激波强度增强，波后压力升高导致再附激波增强；激波/边界层作用点处的逆压梯度增大，流动渐渐分离。由于分离点流线凸起诱导的分离激波强度随之增大，导致分离激波和再附激波相交形成的反射激波增强。

图7为不同边界条件下激波/支板壁面边界层相互作用引起的厚度变化。可以看出，算例1～算例3中反射激波与支板壁面边界层发生强烈相互作用导致边界层厚度增加，同时激波使得干扰区的湍流度增大，促使近壁区流动从层流向湍流转变，使得干扰区下游的边界层比干扰区上游的边界层更厚。算例4、算例5中随着入口马赫数增加，激波强度增加，激波与边界层作用处逆压梯度增大，此时边界层内出现流动分离，导致边界层厚度迅速增加。

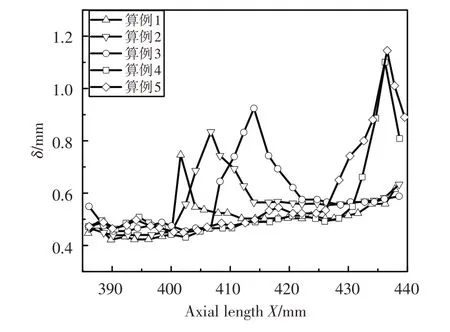
图7 支板壁面边界层的厚度变化Fig.7 Thickness variation of the strut wall boundary layer

3.4 总压损失分析

采用总压损失量化气体穿过激波前后的能量损失。取等直段末端(X=355.0 mm)截面处总压作为参考，图8 给出了不同边界条件下总压损失沿流动方向的分布。可以看出，冷态条件下支板前缘形成的弓形激波较强，穿过此处气流总压损失上升速率较快。随着激波在支板壁面和流道壁面间反射，激波强度渐渐衰弱，总压损失上升速率趋于平缓。到了支板尾缘，由于燃料喷嘴处的斜激波强度大于支板壁面和流道壁面间的反射激波的强度，气流穿过此处时总压损失速率先上升后趋于平缓。算例4、算例5中支板尾缘处的斜激波强度与支板壁面和流道壁面间的反射激波强度相近，总压损失转折并不明显。算例1～算例5随着入口马赫数增加，激波强度增加，导致流动损失随之增加。

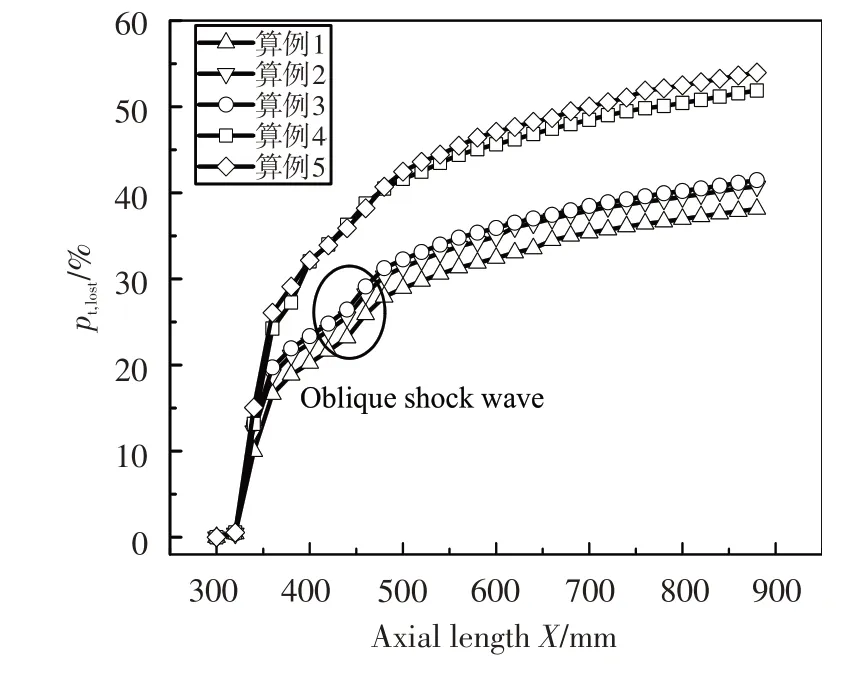
图8 不同边界条件下总压损失沿流动方向的分布Fig.8 Distribution of total pressure loss along the flow direction for different boundary conditions

3.5 模化结果的相互验证

图9 为数值模拟结果(速度散度)和明渠流动结果的对比。可见，激波和水跃波在流场中的结构及变化规律基本一致。但由于明渠流动模型基于二维相似，且忽略了复杂的边界层效应影响，导致激波与水跃波在流场位置上存在一定偏差，使得模化结果存在一定的局限性，有待于进一步模化研究。

图9 流场波系结构实验验证Fig.9 Experimental verification of the flow field wave system structure

4 结论

对支板喷射超燃冲压发动机进行了由激波/边界层相互作用所主导的复杂内流流动特性的模化实验及数值模拟，结论如下：

(1) 对支板喷射超燃冲压发动机燃烧室在不同边界条件下进行了明渠流动模化实验及数值模拟计算，所得的计算结果与模化实验结果相符合，证明了所选数值模型的适用性和模拟方法的可信性。

(2) 随着入口马赫数增加，激波前后气流压力的比值增大，激波强度增加，激波/支板壁面边界层作用点垂直方向逆压梯度升高，导致流动出现分离，且激波角的减小使得激波与支板壁面边界层的作用点向下移动。同时，激波后压力升高，诱导产生的分离激波和再附激波增强，反射激波也随之增强。

(3) 支板前缘处弓形激波较强，总压损失迅速升高，但随着反射激波不断衰弱，总压损失升高速率趋于平缓。

(4) 限于实验条件和资金，本文实验研究只进行了定性分析，不足以进行定量分析，后续工作可以利用相似原理，结合测试技术进行量化分析。此外，对激波/边界层干扰以及其他影响因素，也有待于进一步深入分析研究。