MIPE在临床试验转组研究中的应用*

宋佳丽 孙凤宇 卢宇红 王 策 王 萌 李 康 侯 艳△

【提 要】 目的 本文介绍一种新的处理临床试验转组数据的统计学方法——校正迭代参数法(MIPE)，并通过模拟试验在不同情形下比较MIPE、IPE、意向性分析(ITT)三种方法对治疗效果估计的准确性。方法 通过模拟数据探讨不同的治疗效应真值、潜在预后、转组率等24个假设场景中试验药疗效估计值的差异，并将MIPE、IPE、ITT方法应用于每个场景下进行效果比较。结果 当试验药与安慰剂组疗效存在差异时，ITT和IPE方法得出的治疗效应估计均有偏，这种有偏估计与不同的治疗效应真值、潜在预后和转组率等因素相关，而MIPE方法不受上述因素影响，估计结果较为准确且稳定。结论 MIPE方法不受实际治疗效应、潜在预后、转组率等因素的影响，在各场景中治疗效应估计值的均值较为稳定，与其他方法相比，更接近真实值，在临床试验评价中使用更为可靠。

在肿瘤安慰剂对照设计临床试验中，当被分配到安慰剂组的受试者疾病进展时，让其仍然接受无效措施显然不符合伦理，因此有研究者提出这种情况下应该允许受试者转到试验组接受治疗[1-2]。这种策略不仅仅让研究更符合伦理，而且降低了试验过程中的脱落率，充分利用已经入组的受试者信息。例如，在舒尼替尼治疗伊马替尼失败的晚期胃肠道间质瘤患者的安全性和有效性临床试验研究中，当接受安慰剂的病人疾病进展时，若满足合格标准，可以转组到开放标签的舒尼替尼治疗组[3]。但带来的问题是使用传统方法对这种存在转组情况的研究疗效进行估计时，可能会存在偏倚。例如按照意向性分析原则(intention-to-treat，ITT)会将转组者计入对照组，可能会影响对照组疗效的估计值，从而影响两组疗效的评价[4]；如果按照符合方案原则(per-protocol，PP)则会剔除转组的受试者，这样可能会破坏随机化，造成两组间基线情况不均衡，使得两组疗效的可比性差。因此，急需准确估计具有转组情况的临床试验疗效估计方法。

由于肿瘤疗效评价指标常与总生存期、无进展生存期等时间变量密切相关，所以，目前针对转组问题进行临床试验疗效估计的方法主要围绕在生存数据方面[5]。例如英国国家健康与临床评价研究所(national institute for health and clinical excellence，NICE)认可的等级结构保留失效时间算法(rank-persevering structural failure time，RPSFT)[6]，但这种方法的计算速度十分缓慢。而迭代参数估计算法(iterative parameter estimation，IPE)[7]相较于RPSFT，大大提高了计算的速度，但IPE在估计疗效时会产生偏倚[8-9]。因此，我们提出校正IPE方法(modified IPE，MIPE)。本文将通过统计学模拟试验探索MIPE方法在各种场景下试验药疗效的估计值是否准确。

原理与方法

IPE和MIPE方法通过建立加速失效时间(accelerated failure time，AFT)模型[10]来估计特定处理的真正效应，因此首先介绍AFT模型的基本概念和结构。

1.AFT模型

在一个随机、平行、双盲、安慰剂对照试验中，某一转组受试者i观察到的生存时间Ti(observed time)由其在对照组(C)和试验组(T)中的生存时间组成，即

Ti=TCi+TTi

(1)

假设该受试者i一直在对照组中并未转组接受试验药物，其相应的生存时间称为反事实生存时间(counterfactual event time)Ui，表示为

Ui=TCi+eβTTi

(2)

其中e-β代表加速因子，表示受试者接受试验药治疗的生存时间是接受对照药治疗的e-β倍。若e-β>1，则相较于对照组，试验药使受试者生命延长，其疗效优于对照药；若e-β<1，则表示试验药缩短了受试者的生命，其疗效劣于对照药；若e-β=1，则两种药物的效果并无差异。

将等式(1)代入等式(2)可得

Ui=TCi+eβ(Ti-TCi)

(3)

由于转组患者i在对照组的生存时间TCi即为转组时间(switching time)Yi，则算式(3)可表达为

Ui=Yi+eβ(Ti-Yi)

(4)

整理等式(4)得到下式

Ti=Yi+e-β(Ui-Yi)

(5)

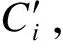
(6)

2.MIPE方法原理和步骤

MIPE通过ITT原则分析获得β初始值，根据初始的β值计算对照组转组患者的反事实生存时间，再将计算得到的对照组的反事实生存时间和试验组的实际生存时间进行比较，更新β值，如此反复迭代，直到两次迭代获得的参数之差小于10-4，此时得到的参数即为所求。IPE方法通过公式(4)和公式(6)计算得到的反事实生存时间和反事实删失时间都和转组时间相关，这种非随机删失可能使得疗效估计值偏离真值。因此，MIPE方法参考RPSFT中的校正思想[6]，对IPE校正再删失规则进行改进，使得反事实删失时间与转组时间无关，避免了IPE方法中可能产生的偏倚。具体规则如下：

(7)

整理后可得

(8)

(9)

MIPE方法应用步骤如下，设第k次迭代估计获得参数βk。

(3)根据步骤(2)估计模型参数βk+1；

(4)当|βk+1-βk|<10-4时达到收敛，此时的βk+1即为β的点估计；否则，k=k+1，从步骤(1)起重复上述循环。

模拟试验

临床试验过程中受试者转组与疾病潜在预后的关系十分密切，所以本模拟试验主要考虑不同的潜在预后结局比例，即在一批治疗患者中预后好的病人所占比例不同的场景；不同潜在预后结局下的不同转组发生率；相同潜在预后结局对生存的不同影响，例如对于不同的疾病，预后好的病人比预后差的病人延长的生存时间会不相同；试验药物不同的实际治疗效果等情况，共模拟24种不同的场景组合。模拟的生存数据服从Weibull分布，故采用Weibull参数回归模型，应用MIPE、IPE、ITT三种方法估计治疗效应，并通过计算各个场景组合下的均值、95%置信区间，以及重抽样方法获得的区间覆盖率来对三种方法进行评估。模拟数据产生和数据分析过程利用SAS 9.4和R 3.6.1软件。本部分主要介绍模拟试验设计下各名词的含义以及条件设定。

1.初始反事实生存时间

初始反事实生存时间u是指模拟试验最开始生成的、不受预后影响的反事实生存时间。初始反事实生存时间服从Weibull分布[11]，其形状参数γ设置为0.5；比例参数λ设置为1.33。利用这些参数生成的u的中位生存时间约为0.639年；病人死亡率随时间降低；未接受治疗的患者90%在随访3年内死亡。

2.入组和出组时间

利用均匀分布函数产生0～1间的随机数，假设病人在试验开始1年内的任意时间均可入组；设定试验周期为3年，则根据不同的入组时间，每名患者的服药删失时间Ci为2～3年不等。

3.病人潜在预后

根据实际情况，相比于预后差的病人，预后好的病人的反事实生存时间Ui更长，因此产生模拟数据时，将数据分成预后好和预后差两组，病人预后好的概率分别设定为0.3或0.75。预后好的病人的反事实生存时间相应延长，可用初始反事实生存时间u乘以膨胀因子，膨胀因子分别设为1.2或3，由此模拟合出预后好和差的病人不同程度的生存差异。同时，生成模拟数据时应该保证试验组和对照组中预后好和差者的比例均衡。

4.转组率和转组时间

如前文所述，预后差的病人在对照组中治疗效果差，更容易转至试验组以寻求好的治疗。因此，根据病人潜在预后情况设定其不同的转组率，预后好和预后差的患者的转组率分别设为：低转组率(0.1和0.25)和高转组率(0.5和0.75)。

假设病人转组时间服从Beta(a，b)分布，则转组时间Yi=反事实生存时间Ui×Beta(a，b)，将分布参数设置为Beta(1，2)可以使转组者平均在其1/3Ui左右时转组，符合很多肿瘤试验发生疾病进展的情况[3，12]。

5.实际生存时间和删失情况

对照组转组和随机分配至试验组的受试者的实际生存时间Ti均在反事实生存时间Ui的基础上进行计算。试验组受试者的Ti=Ui×e-β；转组受试者Ti则通过公式(5)计算。如果病人在试验截止时仍存活，则设定病人生存结局为删失。

6.治疗效应真值

实际治疗效应分别考虑治疗有益、无益和无作用三种情况。当治疗有益时，常见试验药治疗效果是对照药的2倍左右，故取β=-0.8；若治疗无益，假设服用试验药的生存时间是对照药的一半，取β=0.8；如果试验组和对照组患者生存时间相同，则说明治疗无作用，β=0。

7.样本量和重复

样本量为500，按1∶1随机分配到试验组和对照组各250人，本文并不探讨不同样本量对方法的影响，因此充足的样本量可以保证模型的稳健性，从而仅探讨上述影响因素对模型估计结果的影响。

根据影响因素不同水平的组合，共模拟24种不同场景，每种场景重复1000次。影响因素设置情况及其对应的实际意义见表1，各影响因素组合情况见表2。

表1 影响因素总结

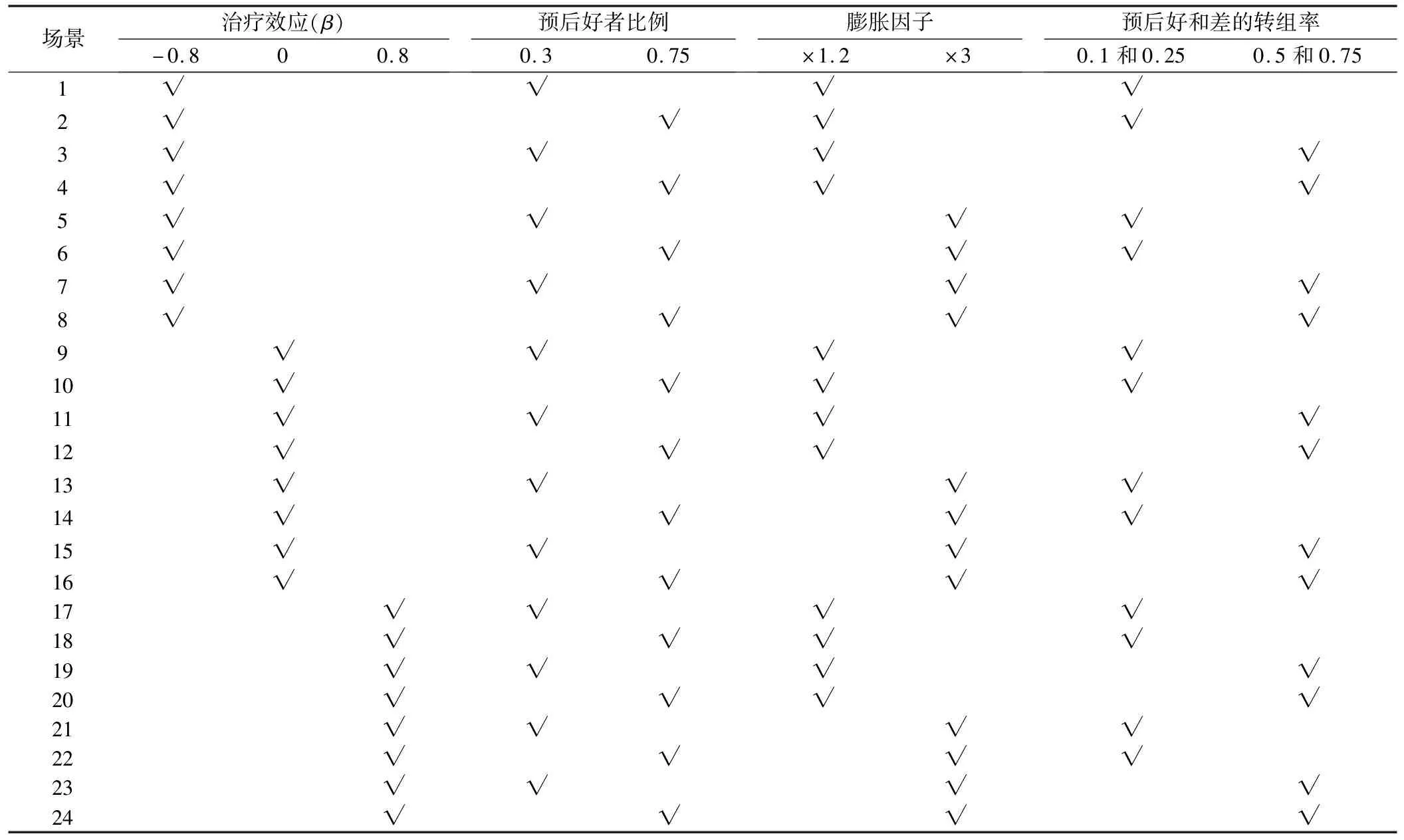
表2 各影响因素组合情况

结 果

1.试验药物效果优于对照组情况(β=-0.8)

模拟试验结果发现当试验组病人生存时间约是对照组2倍时，ITT方法低估了试验组药物真正治疗效果。这种低估现象和转组率、人群中潜在预后效果好的病人比例及预后好者相较于预后差者增加的反事实生存时间程度有关(图1)。转组率越高，低估情况越明显，此因素对疗效估计的影响最大；人群中预后好的病人比例越低，这种低估情况越严重；预后好病人相较于预后差的病人提高反事实生存时间程度越大，对预测治疗效应的影响越大。对于IPE方法，也同样受上述3个因素的影响。而MIPE方法几乎不受上述因素的影响，在各种场景中估计结果较为准确且稳定。

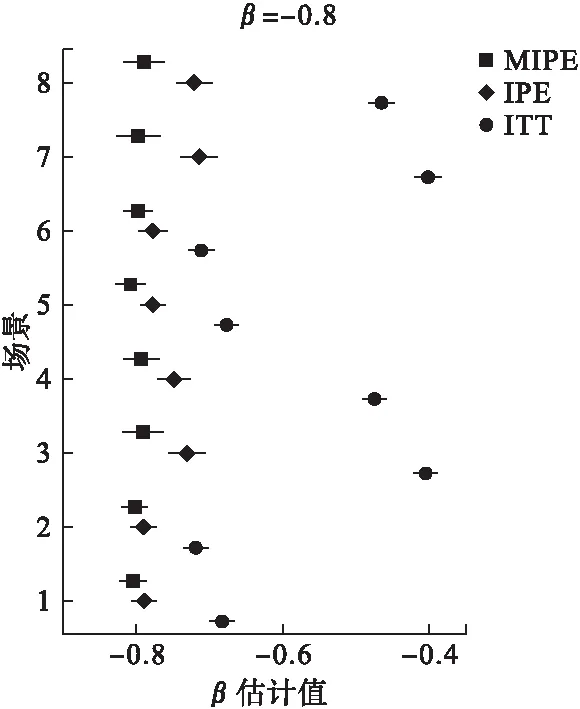
图1 β=-0.8时估计值的均值及其95%置信区间

2.试验组和对照组治疗效应无差异(β=0)

试验组和对照组治疗效应无差异时，按照ITT分析并不会高估或低估对照组疗效，因而对试验组疗效的估计准确。从图2可以看到，使用ITT估计的治疗效应均在0附近，优于MIPE和IPE方法，从侧面反映了本模拟的合理性。

图2 β=0时估计值的均值及其置信区间

3.试验药物效果差于对照组情况(β=0.8)

当对照组病人生存时间是试验组的2倍左右时，ITT和IPE均高估试验药物疗效，即低估了试验药物缩短患者生存时间的作用，而MIPE则一直稳定在真值附近。

我们同时计算了每种场景下，各个方法的区间覆盖率，区间覆盖率为利用重抽样方法求得的95%置信区间包含真值的比例。区间覆盖率应约等于95%，表示95%左右的置信区间包含真值。各场景区间覆盖率值见表3，MIPE的覆盖率值在94.3%～96.1%之间，表明该方法的准确性和稳健性。

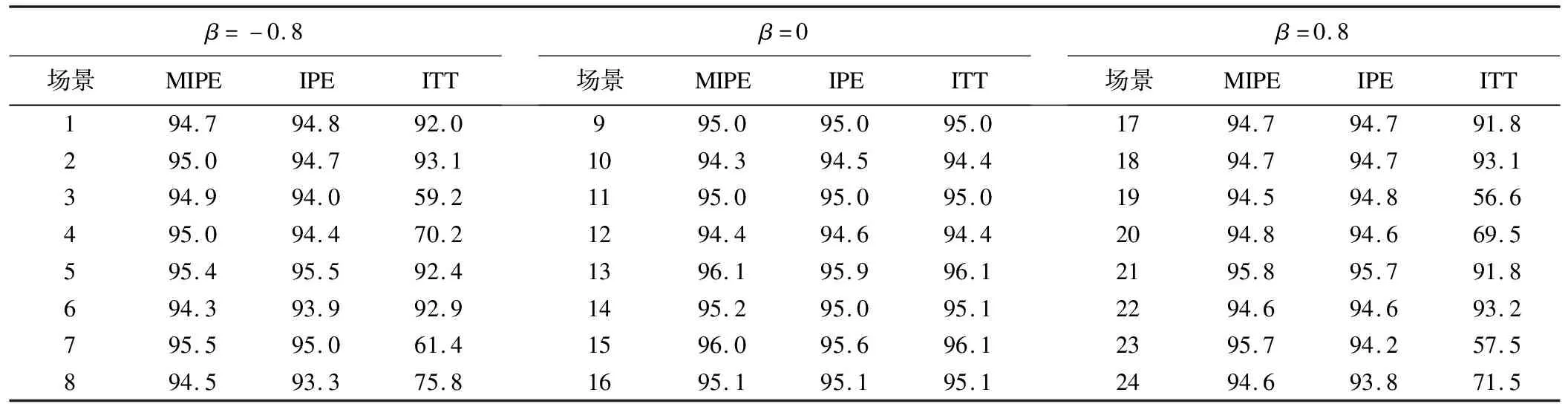
表3 各因素组合场景下区间覆盖率(%)

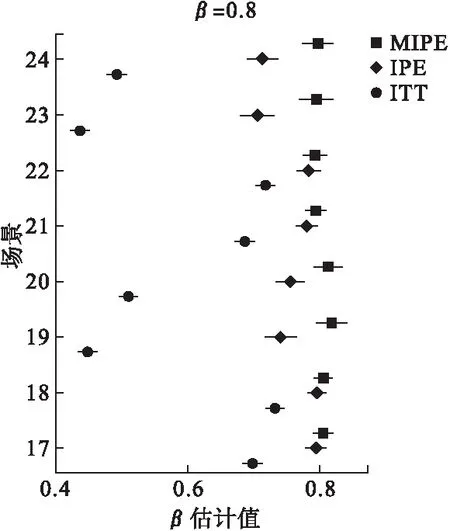
图3 β=0.8时估计值的均值及其置信区间

讨 论

目前常用的RPSFT方法同时计算试验组和对照组受试者的反事实生存时间，并通过网格搜索来估计模型参数，计算速度十分缓慢；IPE方法仅计算对照组中转组患者的反事实生存时间，并使用迭代算法估计参数，可以大大提高计算的速度。但是，其计算的反事实生存时间和反事实删失时间都与转组时间密切相关，这不属于随机删失，因此该方法在估计疗效时会产生偏倚；本文提出的MIPE方法在IPE方法的基础上对其反事实删失时间的计算进行了改进，使得反事实删失时间与转组时间无关，可以有效避免偏倚的产生。

由于MIPE对于IPE进行了部分改进，因此对于可以使用IPE方法进行分析的临床实例，MIPE方法同样适用。如Branson等人使用IPE方法分析一项非小细胞肺癌随机临床试验，比较不能手术的非小细胞肺癌患者立即放疗和延迟放疗的临床益处[7]，以及干预性研究[13]、Concorde临床试验研究[8]、成本效果分析[14]等。并且使用MIPE方法进行分析时，并不需要考虑潜在预后结局、转组率等因素，因为该方法在各种情况下得到的分析结果均稳定。

MIPE方法不仅可以用于肿瘤安慰剂对照设计临床试验转组情况，也适用于其他疾病的安慰剂对照临床试验设计或统一接受标准治疗的加载试验设计发生转组情况时。不过，需要注意的是，当受试者转用其他非试验药物或由对照组转至试验组的患者疗效与初始随机化分配至对照组患者的疗效不同时，MIPE方法则并不适用。

本文中模拟试验仅探究了潜在真实治疗效应、预后结局和转组率等因素对试验药疗效估计值的影响，仍然有很多因素未考虑，如患者的反事实生存时间不服从Weibull分布；潜在预后好和预后差患者转组率差异很大等。未来将继续寻找可能影响治疗效应估计的其他因素，使得模拟场景更贴近实际，探索MIPE方法稳健性。

结 论

通过模拟试验结果可以看出，当试验药和对照药疗效存在差异时，ITT和IPE方法估计的治疗效应均有偏，这种有偏估计与不同的潜在预后结局比例、潜在预后对生存的影响、转组率、真实治疗效应等因素相关，而MIPE方法不受这些因素的影响，在各场景中对疗效的估计均稳定在真值附近，由于实际临床试验过程中，并不清楚人群的具体情况，故MIPE更适合在临床实际过程中使用。