基于 GA-LSSVR 的动力电池SOC 估算研究
容伟,佘世刚,魏新尧,刘爱琦
(1. 常州大学机械工程学院,江苏 常州 213164;2. 常州大学江苏省自动控制实验室,江苏 常州 213164)
0 引言
当今社会的迅速发展,产生了大量的环境污染和传统能源的枯竭等问题,在汽车工业,大力发展电动汽车的工作迫在眉睫[1]。动力电池是当前对电动汽车向前发展的一大阻碍。精准地预测动力电池荷电状态(SOC)对保障行车安全,延长动力电池的使用周期,意义重大[2]。放电试验、电流积分、内阻、开路电压、Kalman 滤波、线性模型和神经网络是目前常见的几种估算 SOC 的单一方法[3-4]。放电试验是一种常用于动力电池的维护和标定的方法,但是实验耗时长,无法动态监测。电流积分是一种相对来说可靠简单且动态监测的方法,具有广泛的应用范围,但是需要获得初始 SOC 值,而且忽略了电池内部的一些化学变化,如果长期使用需引用相关修正系数才可减小误差。仅通过内阻法来预测电池 SOC 的精度受到的影响因素较多,所以单一的内阻法一般不应用在生活中。开路电压法是一种应用范围宽泛的电池 SOC 估算方法,且能够有效地提高估算精度,但是实验前的准备时间较长。线性模型方法适用于铅酸电池这种电流较小的电池,相对来说应用范围小。Kalman 滤波法适用于汽车动力电池在工况复杂环境下的 SOC 估算,但是精确度与电池模型的准确度相关,而且动力电池的非线性工况出现的误差较大。神经网络是一种可忽略电池内部变化且估算精确度较高的方法,但是训练的样本数据较为繁琐,花费时间较多,导致其计算量大,对实验硬件要求高。
最小二乘支持向量机(LSSVM)算法的优点是选择简单,泛化能力强大,收敛范围大,可替代神经网络法[5]。其基本思想是建立高纬空间的最优超平面,利用最小二乘法对所有样本进行误差拟合。其缺点是计算复杂度大概是样本数的三次方量级,计算量巨大。针对支持向量机(SVM)计算量较大的问题,最小二乘支持向量回归机(LSSVR)优化其结构,利用等式替代不等式,大大降低预算量,缩短运行时常。LSSVR 中的重要参数通过遗传算法(GA)来选择优化,能够显著提升动力电池 SOC 的预测精度[6]。
1 电池模型
1.1 建立电池模型
用普通的电压源、电容和电阻等元件来搭建动力电池的等效电路模型,基于 RC 网络来表达其动态特性。为了兼顾动力电池的暂态和稳态特性[7],等效电路模型选择二阶,如图 1 所示。Voc表示电池开路电压;V 表示电池端电压;Rts和 Cts表示活化极化电阻和电容;Rtl和 Ctl表示浓差极化电阻和电容;Ccap表示目标电池容量;Ibat表示目标电池充放电电流;Rs表示等效串联电阻。
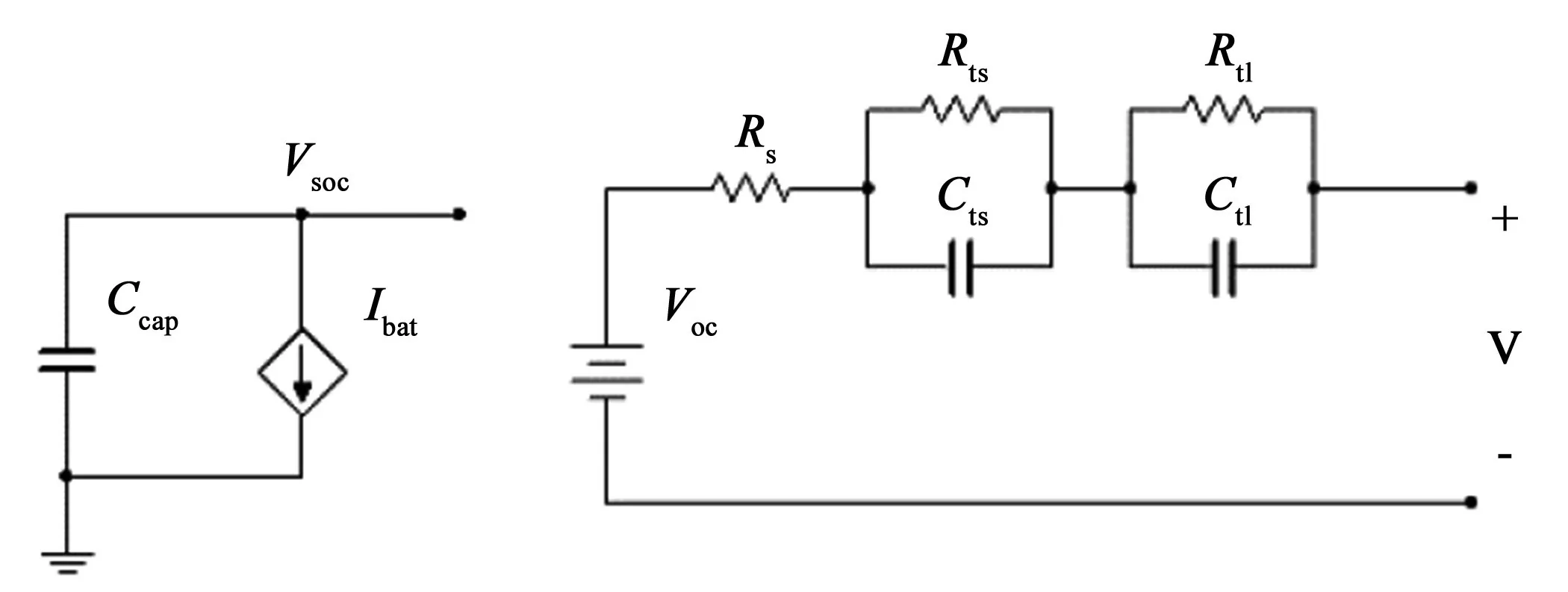
图1 等效电路图
动力电池 SOC(用 ζSOC表示)与开路电压的函数设为 g(x),设状态变量 x1、x2、x3,对应动力电池 ζSOC、Ucts、Uctl,输入 u 为 Ibat,输出 y 为通路电压 v,建立状态方程
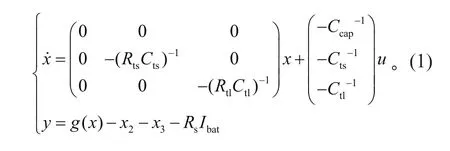
将式(1)离散化,可得到的时间方程:
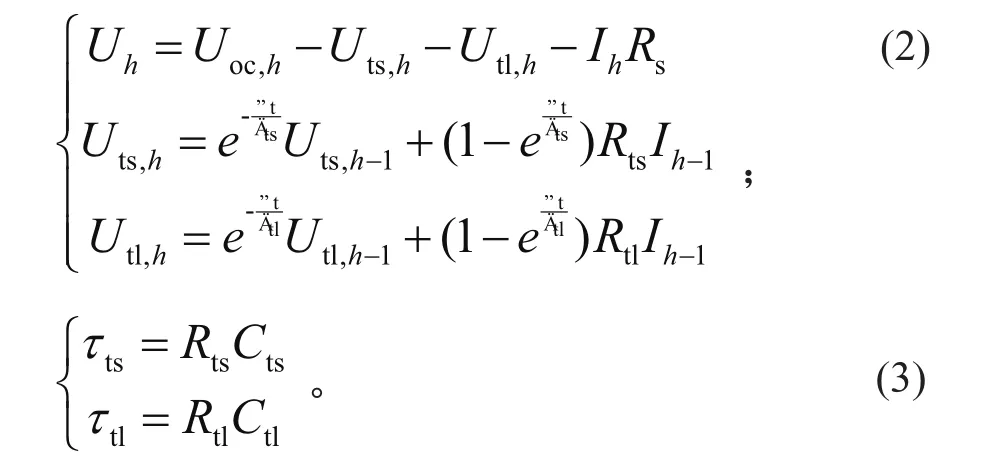
式中:h 时刻电池的端电压、活化极化电压、浓差极化电压和开路电压分别对应 Uh、Uts,h、Utl,h、Uoc,h;Δt 是模拟动态响应的采样时间;τts和τtl分别是模拟电池动态响应时的短时间常数和长时间常数[8]。
通过安时积分法来计算动力电池的 SOC,其计算方程为
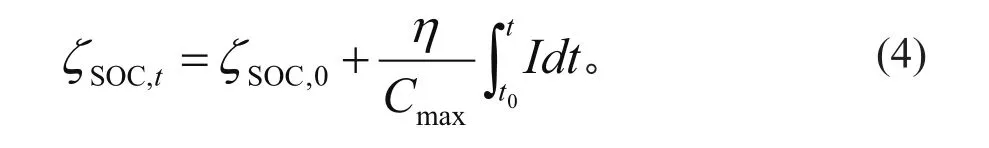
式中:动力电池的最大容量用 Cmax来表示;t0时刻的荷电状态用ζSOC,0表示;η是比例系数。
1.2 参数辨识
控制 25 ℃ 的实验温度,选择型号为 BD4820CD,额定电压是 48 V,额定容量是 20 Ah 的动力电池来进行试验。对该电池做混合动力充放电实验HPPC,测得表 1 所列开路电压值[9],得到图 2 所示电压变化规律。

表1 开路电压表
从图 2 可知,动力电池欧姆内阻的变化导致U1~U2和 U3~U4之间电压快速变化。动力电池的极化现象是导致 U4~U5之间电压轻微起伏的原因。将二阶 RC等效电路模型与 U4~U5之间的电压变化和时间拟合,从而得到参数 Rts、Cts、Rtl和 Ctl,根据不同的 SOC 值,可得出表 2 所列各参数值。

表2 等效模型参数识别

图2 电压变化曲线图
2 分析最小二乘支持向量回归机的应用


式(5)中,ω 为权重向量,b 为偏置。在 SVM 中,约束条件为不等式:

通过上式可知 SVM 的计算复杂,计算量庞大,所以提出最小二乘向量回归机(LSSVR)将上述不等式问题转化为等式问题,参考下列公式(7),减少计算量,并保留 SVM 在高纬空间的拟合能力[10]。

ξ是一个松弛变量,e 是优化目标的松弛变量,γ 和 c 都是寻找最优超平面和偏差最小之间平衡的一个权重。原问题可由拉格朗日乘数法转变为优化对偶向量 α 的问题。
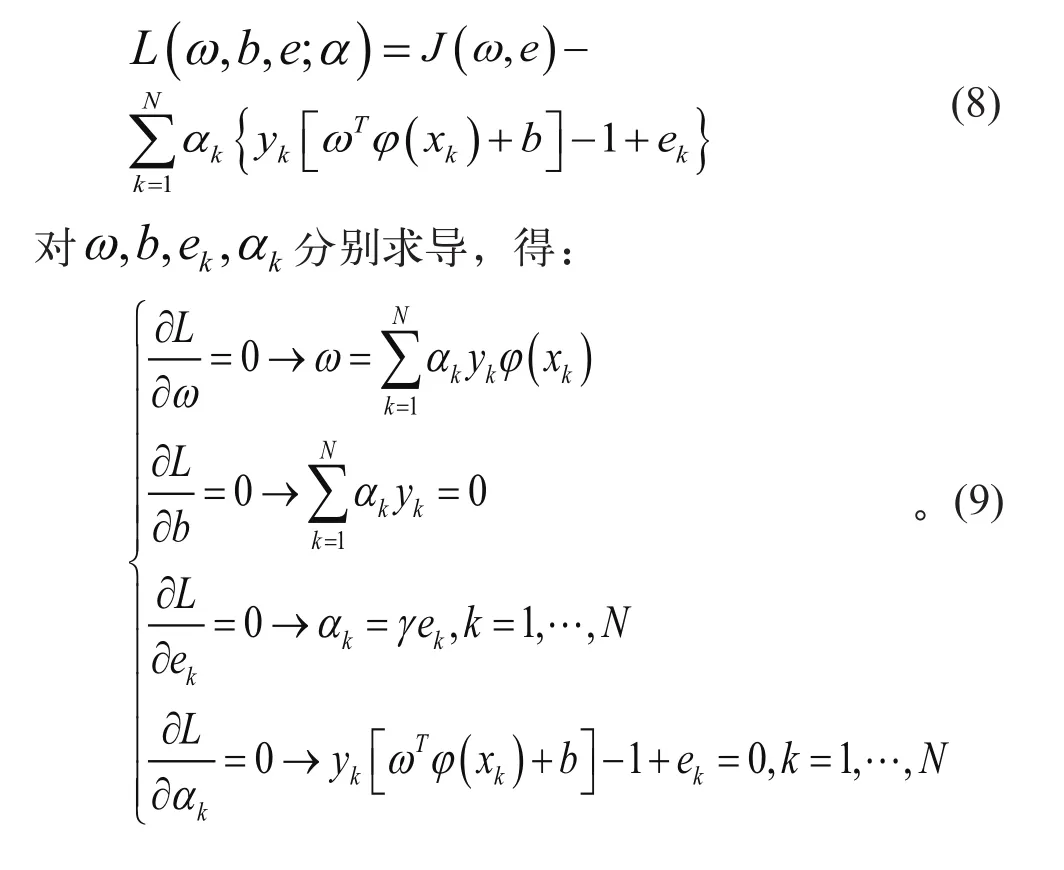
令 yk为 y = f (x) 中的 y,由上式可得线性方程组
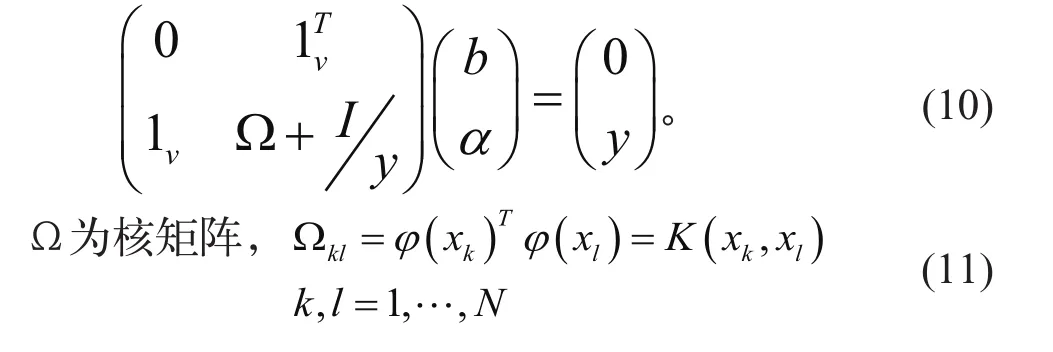
由上式可知,要解决其核矩阵只用求得高纬空间内积或者核矩阵即可。二者取其轻,核函数更容易计算。核函数常用的有多核式、径向式和sigmoid。针对以上核函数,其表达式如下:
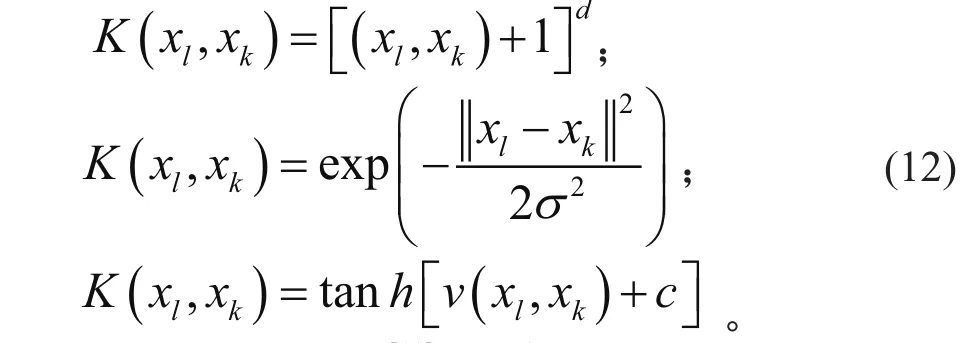
在此采用径向核函数[11],σ2表示函数宽度参数。解得 LSSVR 函数为
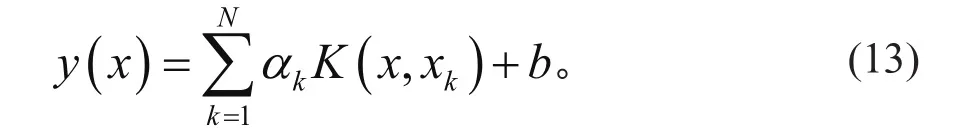
此方法现已广泛应用在工程实际问题中,其预测准确性和 γ 和 σ2这两个参数紧密相关。γ 和σ2的值都是经过大量的训练运算,优选出的一个区间范围,难以确定一个准确的数值,使 LSSVR达到最佳性能,故这个方法存在一定的缺陷。
3 GA-LSSVR
由于 γ 和 σ2的值只通过以上算法难以确定一个准确的数值,从而不能 LSSVR 达到最佳性能。为了寻找 γ 和 σ2的最佳值,在此学习机的基础上,使用优胜劣汰的遗传算法(GA)进行优化,不仅让上述算法的运算量降低,而且能进一步提升电池 SOC 预测精准度。相较传统算法,遗传算法具有多线程处理,优异的可操作性,全局寻优和目标清晰等特点[12]。遗传算法是将生物界的进化论应用到待解决的问题中,自适应选出相符条件的个体,将不适应个体经过交叉变异进化成想要的个体,形成新的种群,不断“优胜劣汰”,复制进化,经过多次迭代,得到近似的最优解[13]。
遗传算法主要有以下几个步骤:
1)编码:根据遗传变异进化的规律将实际问题进行编码。常用的几种编码方式有格雷编码,实数编码和二进制编码。由于二进制编码操作简单,在进化程度上易于实现,故采用二进制进行编码。
2)适应度函数:遗传给后代的基因大概率都是适应度高的个体,而个体中适应度低的基因被淘汰。对于择优问题,通常选择统一化变换的适应度函数。
3)遗传算子(选择、交叉、变异):优先选择适应度高的个体,将适应度低的个体中的染色体交叉产生新的个体,再重复上述步骤,进行优化迭代选择。
4)参数设定:定义 Pc为交叉概率,Pm为变异概率,l 为染色体长度,Np为种群规模。根据相关研究经验总结可知,Pc的范围值为 0.5~0.8,在此取值为 0.6。Pm的范围值为 0~0.05,在此取值为0.03。Np的范围值为 20~200,在此取值为 100。
5)终止算法:适应度达到期望,就停止运行,否则进行遗传算子达成新的群体,循环选择,直到最大迭代数,淘汰掉适应度低的个体,输出最优解。
按照以上步骤得到如图 3 所示流程。

图3 遗传算法流程图
4 仿真分析
在 Matlab 中的 optimtool 工具箱中实现遗传算法优化,得出 γ 和 σ2的最优解值分别为 18.1956和 2.7361。以 BD4820CD 电池作为动力电池源,模拟车辆的一个循环工况,得出动力电池的工作电压、电流、温度和响应的 SOC 变化,建立 GALSSVR 模型,输入循环工况中的端电流、端电压和温度变化值,估算电池 SOC 值。动力电池运行一个循环工况周期,SOC 值下降了 4 %,各参数变化如图 4 所示。

图4 参数变化图
采取均方根误差(RMSE)公式

来预测 GA-LSSVR 模型的好坏。式中:M 为测试样本数,Yk是 SOC 估计值,yk是 SOC 真实值。仿真得到误差如图 5 所示[14]。

图5 估算 SOC 误差
5 结论
通过对传统的一些动力电池 SOC 估算方法中存在的优缺点进行比较研究,选用 GA-LSSVR 来估算动力电池 SOC 值,通过 Matlab 进行仿真,能够在保证实用性的基础上明显降低动力电池SOC 的估算误差[15],进一步把误差值稳定地控制在 3 % 以内。

