GMSK信号的同步及相干解调算法

陈丽婷，康 超，顾圣明，陈建斌

(上海航天电子技术研究所，上海 201109)

0 引言

高斯最小频移键控(Gaussian Filtered Minimum Shift Keying，GMSK)是调制指数为1/2，频率脉冲响应为GMSK脉冲的连续相位调制(Continue Phase Modulation，CPM)。GMSK包络恒定、相位连续，使得其带外辐射功率小、谱密度集中，并且由于其相位具有记忆性，使得其具有一定的纠错能力。因此，GMSK具有较高的频带利用率、功率利用率，适合在无线通信信道传输[1-4]。在频带资源有限的数字通信领域，GMSK得到广泛的应用，如全球移动通信系统(GSM)、遥测靶场系统、航空数据链以及空间数据传输等。

GMSK的解调算法有非相干解调和相干解调。非相干解调不需要恢复相位，算法简单，易于实现，但灵敏度损失较大。GMSK的最佳解调算法是最大似然序列检测(Maximum Likelihood Sequence Estimation，MLSE)算法，使用MLSE解调算法的关键是载波相位同步以及符号定时[5-7]。文献[8]基于最大似然算法对载波相位和符号定时进行了联合估计，运算比较复杂；文献[9]对接收采样数据进行FFT运算后进行载波频偏和符号定时的联合估计，运算量与最大似然算法相比有所下降，但运算量仍较大，并且该算法需要有训练序列，增加了系统开销。

本文采用了通用数字环+符号定时+维特比译码实现GMSK的相干解调。通用数字环是一种低计算量和适合数字化处理的锁相环路，在此基础上提出一种改进算法以提高环路的性能；提出的一种符号定时的新算法实现GMSK信号的位同步，该算法基于GMSK信号波形特点，算法简单，易于实现；采用基于最大似然原理的维特比算法实现GMSK解调，并提出简化算法。

1 GMSK信号特性分析

GMSK信号可以表示为：

(1)

式中，Es为码元能量；T为码元周期；f0为载波频率；φ0为初始相位；φ(t,α)为相位信息，可表示为：

(2)

式中，α={αk}，表示二进制的发送码元序列，取值范围为{+1,-1}；调制指数h=1/2；脉冲相位函数q(t)是一个连续单调函数，可以由频率脉冲响应g(t)的积分来表示，即：

(3)

-∞≤t≤∞，

(4)

(5)

式中，Bb为预调制高斯滤波器3 dB带宽。BbT值越小，高斯脉冲响应时间越长，波形越平滑，信号功率谱旁瓣衰减的越迅速，但码间干扰也越严重。当BbT值趋近于无穷大时，GMSK信号成为MSK信号。

由于g(t)的区间为-∞≤t≤∞，在工程上不容易实现，因此可以将之截短为：

(5)

对于GMSK信号，不同BbT值的g(t)波形在各个码元周期T内的面积如表1所示。从表中可以看出，g(t)的波形主要集中在(-2.5T～2.5T)中，因此，在工程实际应用中，可以将g(t)截短为5T的宽度，即N=2。

表1 不同BbT值的g(t)波形在各个T宽度内面积

不同BbT值下GMSK信号的功率谱能量分布如表2所示。由表2可以看出，BbT值越小，谱密度越集中，频带利用率越高。

表2 不同BbT值的GMSK能量分布

使用MATLAB SIMULINK的GMSK Demodulate Baseband 模块仿真得出基于MLSE相干解调的误码率，由于该模块具有较好的性能，因此把该误码率作为理论误码率，作为与工程实现性能对比的依据。不同BbT值下GMSK信号的误码率曲线如图1所示，可以看出，BbT值越大，解调性能越好。综合考虑功率利用率和频带利用率，在实际工程应用中，选择BbT=0.25。

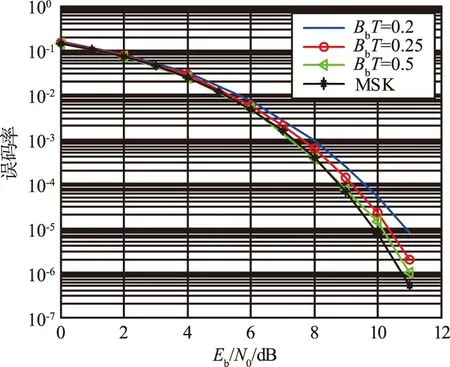
图1 不同BbT值的GMSK的误码率曲线Fig.1 GMSK error rate curves of different BbT values

2 GMSK相干解调系统

2.1 载波同步环路

GMSK接收机的相干解调不仅要补偿频偏，还要恢复载波相位。文献[10]分别仿真了判决反馈环和通用数字环对GMSK信号相位跟踪的S曲线，结果表明在特定BbT范围，判决反馈环和通用数字环均能够恢复GMSK信号的载波相位。其中，通用数字环的BbT适用范围0.15～0.4，大于判决反馈环的适用范围(0.15～0.3)，鉴相灵敏度也大大高于判决反馈环。本文采用通用数字环，其原理框图如图2所示。

图2 通用数字环原理Fig.2 Block diagram of universal digital loop

环路滤波器输入端的误差信号为：

F(t,θ)=sgn[sinφ]×sgn[cosφ]×

sgn[sinφ+cosφ]×[sinφ-cosφ]。

(7)

环路滤波器的选择在很大程度上决定了环路的捕获性能、跟踪性能以及抗噪性能，对于相干解调来说，相位噪声对解调性能有很大的影响。本文采用的是一阶环路滤波器，其原理框图如图3所示。

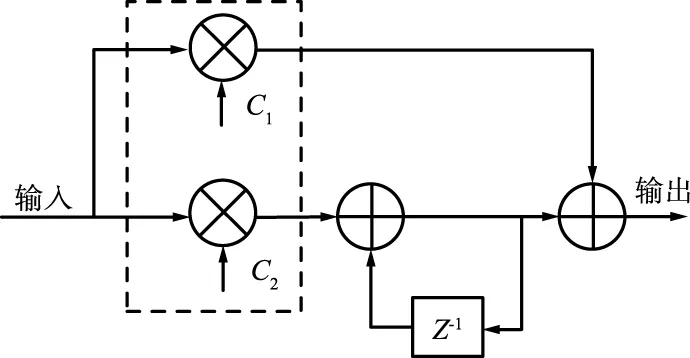
图3 一阶环路滤波器原理Fig.3 Block diagram of first order loop filter

系统传输函数为：

(8)

(9)

图2虚线框中乘法器的输入为+1或者-1，因此可用异或逻辑代替虚线框中的乘法器；图3一阶环路滤波器的输入为+1或者-1，因此可用加法器来替代虚线框中的乘法器，使其资源更加优化。由上述可知，本文使用的通用数字环结构简单，鉴相器及环路滤波器在实现过程中只需要若干个加法器，计算量低，适合数字处理。

在误码率为9.4×10-5时，相干解调理论的Eb/N0=9.2 dB，因此在载波环路仿真时，令AWGN信道的噪声值Eb/N0=9 dB。载波环路跟踪曲线如图4所示，可以看出，当BL=0.01Rb，载波频偏为50 kHz时，捕获时间约为0.069 s,相位波动小；当BL=0.01Rb，载波频偏为100 kHz时，载波环路无法收敛；当BL=0.05Rb，载波频偏为100 kHz时，捕获时间约为0.002 s,相位波动大。为了使环路具有较快的捕获速度、较大的捕获范围，以及较小的相位波动，采用环路参数切换策略，在捕获阶段令BL=0.05Rb，在跟踪阶段令BL=0.01Rb，频偏为100 kHz的载波环路跟踪曲线如图5所示。

图4 载波环路跟踪曲线Fig.4 Tracking curve of carrier loop

图5 改进后的载波环路跟踪曲线Fig.5 Tracking curve of improved carrier loop

可以看出，捕获时间为0.002 s，相位波动小。在最大的多普勒捕获范围内，均可以采用此种载波环路跟踪策略。

2.2 一种新的符号定时算法

在AWGN信道下，GMSK接收机接收信号可以表示为：

r(t)=s(t,α)+n(t)，

(10)

式中，s(t,α)为发送信号；n(t)为高斯白噪声。假设经过载波环路之后，接收信号的频率与相位均已恢复，则可得到基带数据I路和Q路：

(11)

GMSK信号是连续相位调制信号的一种，其调制信息包含在相位信息φ(t,α)里，即：

(12)

BbT=0.25的GMSK相位轨迹，如图6所示。

图6 BbT=0.25的GMSK相位轨迹Fig.6 GMSK phase of BbT=0.25

图7 [0,2π]内cosθ与sinθ的波形Fig.7 Waveform graph of cosθ and sinθ within [0,2π]

本文基于GMSK基带信号波形的这个特性，提出一种符号定时的新算法。综合观测图6和图7可以得出：

① 码元周期的起始时刻是I(t)和Q(t)的极值点或者过零点。

② 为了增加该算法的抗干扰性，选择合适的时间进行统计，选取概率最大的时刻作为码元周期的起始时刻。

令AWGN信道的噪声值Eb/N0=9 dB，每个码元采样点数为5，表3给出了在不同统计时间下本文提出的符号定时算法的判决概率。从表3可以看出，随着统计时间的增加，定时精确度越高，在工程实现中，根据对定时速度以及精确度的实际要求，选择合适的统计时间。

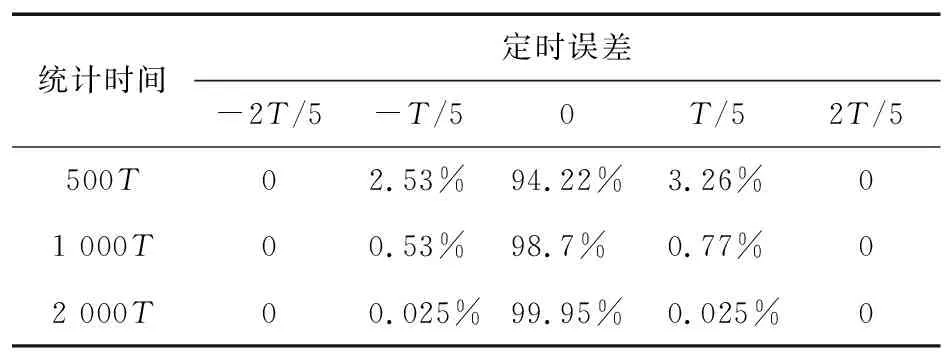
表3 符号定时算法判决概率

文献[11-12]中的GMSK符号定时算法采用联合相位定时恢复算法和联合频偏定时估计算法，具有较好的定时性能，但均需要使用大量的乘法器。本文提出的符号定时算法复杂度低，在工程实现中不需要使用乘法器，运算量少，占用的硬件资源极小，在资源受限的工程应用环境中，具有明显的优势。

2.3 基于MLSE的维特比解调

GMSK信号的相位具有记忆性，其最佳解调算法是MLSE算法。MLSE是基于最大似然原理，在接收端假设所有可能的发送序列，计算它们与接收信号的相关性，从而完成符号序列的整体判决[13-14]。

假设信道为AWGN信道，MLSE将会选择与接收信号r(t)具有最小欧式距离的信号s(t,α)所对应的符号序列α作为判决输出，即：

(13)

由于GMSK为恒包络信号，式(13)的最小化等价于最大化相关，即：

(14)

式(14)右边可以用维特比检测算法递归计算得到，即：

(15)

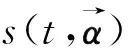
在工程实现时选择FIR滤波器实现匹配模块，与128个本地参考波形进行匹配滤波，将本地参考波形的数值作为FIR滤波器的系数，每个本地参考波形采用一个FIR滤波器实现，因此该匹配过程需要128个FIR滤波器，对硬件资源需求大。本文根据I(t)和Q(t)波形特性，提出了简化算法。

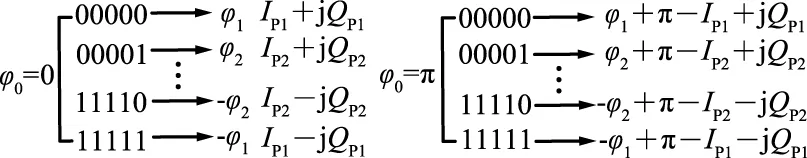
图8 维特比匹配滤波器模板Fig.8 Matched filter pattern of Viterbi

3 工程实现

基于FPGA XC7K160T平台，实现GMSK相干解调算法，包括载波同步，符号定时以及基于MLSE的维特比解调。

输入信号以及算法参数：

① GMSK信号,BbT=0.25，码速率Rb=10 Mb/s；

② 载波环参数：捕获阶段BL=0.05Rb，跟踪阶段BL=0.01Rb；

③ 符号定时统计时间：1 000T；

④ 维特比观测长度：5T。

工程测试框图如图9所示，包括RS SMW200A信号源、FPGA XC7K160T平台和误码率显示计算机。实际的硬件设计和验证平台如图10所示。

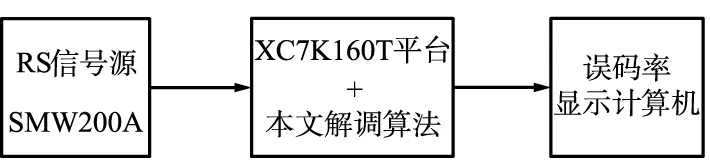
图9 GMSK工程测试框图Fig.9 Block diagram of GMSK engineering test

图10 硬件设计和验证平台Fig.10 Hardware design and verification platform

图11给出了该解调系统在图10硬件平台下的误码率实测曲线以及理论的最佳解调误码率曲线,其中输入信号BbT=0.25，码速率Rb=10 Mb/s。从图中可以看出，当Eb/N0≥8 dB时，本文算法的误码率曲线与理论值趋于一致，在误码率为9.4×10-5(系统链路环境使用要求)时，本文算法灵敏度为9.5 dB，比理论值9.2 dB仅恶化了0.3 dB，解调损耗小，性能优良。

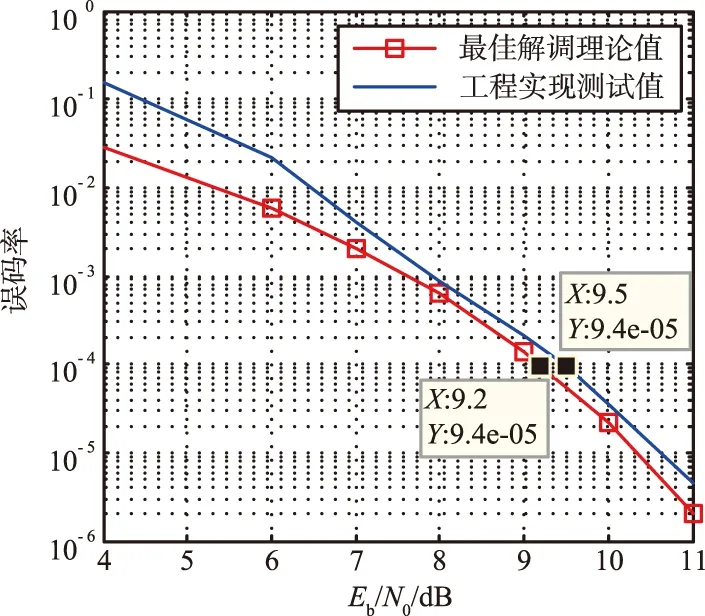
图11 GMSK(BbT=0.25)误码率曲线Fig.11 Error rate curve of GMSK(BbT=0.25)

4 结束语

使用MLSE解调算法的关键是载波相位同步以及符号定时，本文采用通用数字环进行载波相位的同步，环路参数影响载波频率的捕获范围、锁定时间以及相位误差，通过环路参数的切换在这三者中取得最优的平衡，以提高环路的性能。仿真结果表明,本文提出的改进算法使得环路具有更大的捕获范围，更快的捕获速度以及更小的相位波动。GMSK的相位调制特性决定了其I路与Q路信号在码元周期内具有单调性的特征，本文基于该波形特点提出了一种符号定时的新算法，仿真结果表明，该算法复杂度低，运算量少，易于工程实现，定时精度符合相干解调的要求。由于GMSK的码间干扰特性，本文采用维特比算法来实现最大似然解调，并提出简化算法，使得占用的FIR资源减小为原来的1/4。工程实现表明，基于本文算法的GMSK相干解调系统误码率性能仅比理论值恶化0.3 dB，性能优良。