一种三维转台系统角度误差校正算法
陈 祎,雷舒杰,赵勇武,王 昭,蔡 晔
(上海无线电设备研究所,上海 200090)
0 引言
在航空、航天、兵器和船舶等军工应用领域中,雷达系统和三维转台系统相辅相成[1]。雷达是一种不可或缺的探测装置,三维转台是非常重要的辅助测试设备。雷达系统中的大部分性能指标测试都是在转台系统上进行,转台系统的定位精度将很大程度上对雷达系统的指标测量造成影响。
雷达系统通常是安装在转台系统上进行测试的。受结构尺寸、安装孔位和定位误差等因素的限制,很难保证雷达系统天线回转中心与转台转动中心完全重合。因此方位、俯仰和横滚任何一维存在安装角度偏差,都会对雷达目标角度测量造成影响[2];另一方面,转台转动也会存在方位俯仰角度的耦合,使得转台真实定位位置与理想定位位置出现偏差。因此,必须进行转台误差校正才能使转台角度更加精确可信[3-10]。
在进行雷达测角误差指标评估时,以上2个方面的问题会导致该指标测试结果恶化,进而影响雷达测向性能的评判。针对此问题,本文在主被动复合雷达的基础上,提出了一种转台安装及角度耦合校正算法。利用主动雷达较高的跟踪精度(小于0.1°)来修正系统的安装误差;并推导了转台方位俯仰角度之间的耦合误差公式,利用该误差对转台角度进行校正。仿真结果表明,本算法能够有效地消除系统安装及耦合误差,大大地提高了转台定位角度的置信度,提升雷达系统性能的测评精确性。
1 安装误差校正
转台安装误差校正示意图如图1所示。在进行系统安装时,既要保证雷达系统、工装和转台系统的安装关系一致,又要保证雷达天线回转中心与转台的回转中心一致。在实际安装时只能首先保证雷达系统、工装和转台安装关系一致,而因为转台内轴尺寸限制,天线回转中心就会超出转台的回转中心。虽然经过优化设计工装,能够让雷达系统与转台系统处于同一水平切面,即保证天线不存在滚动角偏差。2个回转中心不重合会对雷达系统角度测量值带来影响,需要采用补偿方法计算出其理论测角值。
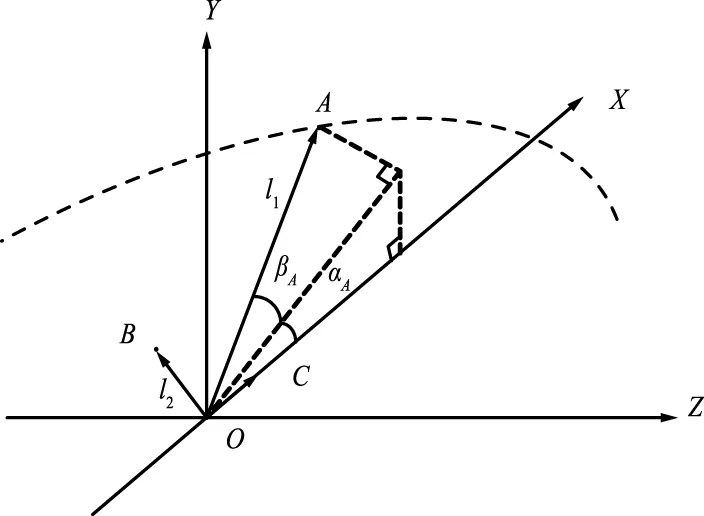
图1 转台安装误差校正示意Fig.1 Schematic diagram of the turntable installation error correction
设点A为测试暗室中的阵列目标点,B为雷达天线回转中心,O为转台回转中心,OA在OXYZ坐标系中的俯仰、偏航和滚动为(αA,βA,γA),转序为先俯仰再偏航最后滚动;阵列面阵到转台回转中心的距离OA=lA,OB在OXYZ坐标系中的俯仰、偏航和滚动为(αB,βB,γB),转序为先俯仰再偏航最后滚动,OB=lB;在雷达天线坐标系OBY′Z′下BA的理论俯仰角、理论偏航角为(αBA,βBA),雷达天线转序同样采用先偏航再俯仰。

(1)
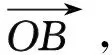
(2)
OA在导引头天线坐标系OBY′Z′中的向量表示如下:
(3)
OB在雷达天线坐标系OBY′Z′中的向量表示如下:
(4)
在ΔOAB中,以上向量存在如下关系:
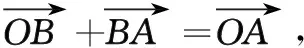
(5)
即有:
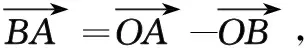
(6)
所以有:
(7)
在直角坐标系OBY′Z′中已知2点A和B的坐标,可求得它们之间的方位俯仰角度为:
(8)
首先主动雷达开机,让主动雷达处于稳定跟踪状态,并记录下此时主动伺服机构的反馈角度。阵列目标不动,转台动时,阵列目标在零位不动(αA,βA,γA)=(0,0,0),转台设定角度(α′B,β′B,γ′B)=(α′B,β′B,0),其中OA=lA=20 m,OB=lB=XX(未知)。但伺服方位俯仰角度反馈均为0°时,停止转动转台,并记录下此时转台角度(α′B,β′B,0),此角度即为天线回转中心的安装误差(αB,βB,0)。
同理,在试验过程中,转台不动,阵列目标动时,阵列目标设为(αA,βA,γA)=(αA,βA,0),转台设定角度为(αB,βB,γB)=(0,0,0),其中OA=lA=20 m,OB=lB=XX。主动雷达开机,让主动雷达处于稳定跟踪状态,并记录下此时主动伺服机构的反馈角度。目标阵列缓慢移动,当主动伺服机构反馈角度为0°时,目标阵列停止移动,并记录下此时目标位置与原始位置之间的距离,此距离即为lB。
通过上述方法可以获得天线回转中心和转台转动中心的位置偏移量(αB,βB,lB)。再由式(1)~式(8)可以获得雷达目标之间的理论值(αBA,βBA),从而可以正确评估雷达测量值与目标真实值之间的差异。
2 转台耦合校正
由于转台在转动过程中方位俯仰角度存在耦合,所以期望角度和真实转动角度之间存在耦合误差,必须予以消除才能降低对雷达测角误差的影响。
转台转动角度示意如图2所示,O为坐标原点,Z为转台目标视线方向,T为目标,P,M分别表示T在XOZ平面、XOY平面的投影点,天辐射源T的视线角为φ,方位角为θ,航向角为α,俯仰角为β。
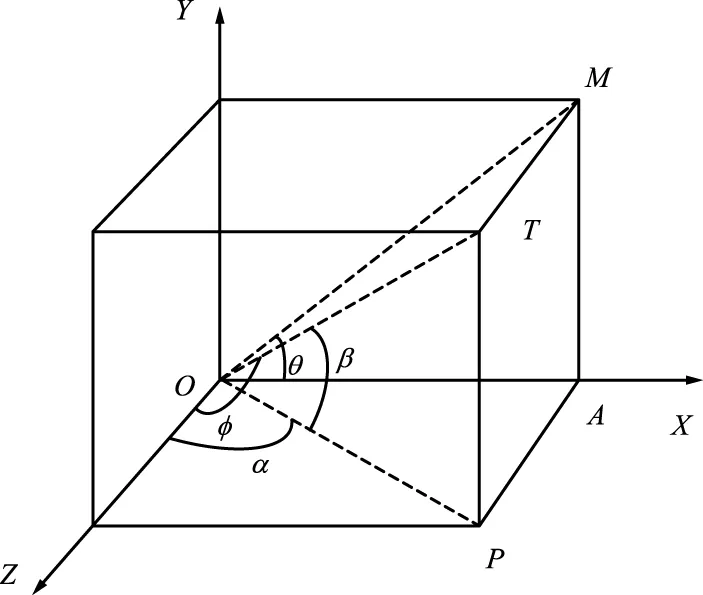
图2 转台转动角度示意Fig.2 Rotation angle diagram of turntable
假设PT=1,则OA长度LOA为:
(9)
OM长度LOM为:
(10)
PA长度LPA为:
(11)
因此OT长度LOT为:
(12)
在ΔOAP中,有:
(13)
在ΔOTP中,有:
(14)
综上,视线角φ,方位角θ,航向角α,俯仰角β满足如下关系:
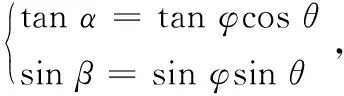
(15)
或者:
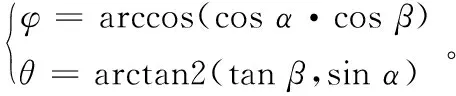
(16)
在转台实际转动过程中,可以将转台反馈角通过式(15)求出其真实目标角度。
3 测角误差评估
在本雷达转台目标测试系统中,目标角度测量误差的均值和标准差按式(17)~式(20)进行计算。
目标方位角测量误差均值为:
(17)
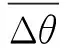
目标方位角测量误差的标准差为:
(18)
式中,σθ表示目标方位角测量误差的标准差,单位(°)。
目标俯仰角测量误差均值为:
(19)
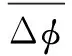
目标俯仰角测量误差的标准差为:
(20)
式中,σφ表示目标俯仰角测量误差的标准差,单位(°)。
在角度测试过程中,可先不对转台安装及耦合误差修正,按照式(17)~式(20)的计算方法或者不校正测角误差;再利用第1节和第2节的校正算法对转台角度进行校正,经同样的测试可获得校正后的测角误差,这就可以对以上校正算法的校正效果进行有效评估。
4 仿真分析
4.1 安装误差仿真
目标相对转台的距离为20 m,目标在阵列面上做方位10°、俯仰±20°、频率为5 Hz的正弦运动。转台回转中心坐标为(0,0,0),雷达天线回转中心坐标为(0.07,0.10,0.2)。转台安装误差带来的测角误差如图3所示,转换的角度信息为αB=19.29°,βB=26.57°,数据采样频率为100 Hz,总采样点数为100。
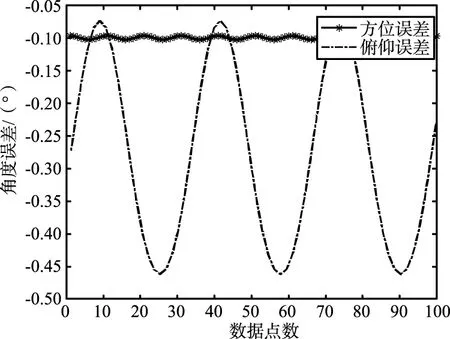
图3 转台安装误差带来的测角误差Fig.3 Angle measurement error caused by installation error of turntable
由图3可以看出,转台安装会带来额外的并且按照一定规律变化的测角误差,这个误差必须予以消除才能准确评估雷达测角精度。
4.2 耦合误差仿真
目标相对转台的距离为20 m,且目标在阵列面上做俯仰20°、方位±20°、频率为5 Hz的正弦运动。转台回转中心坐标为(0,0,0),雷达天线回转中心坐标为(0.07,0.10,0.2),据采样频率为100 Hz,总数据采样点数为100点。按照第3节的计算方法可获得转台方位俯仰角度耦合误差,如图4所示。
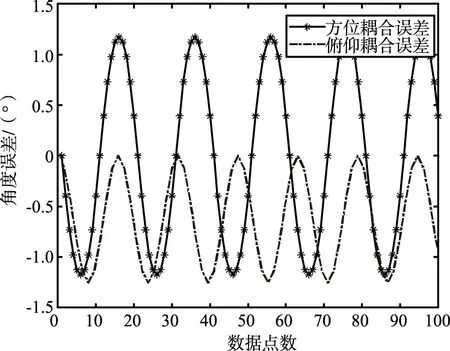
图4 转台方位俯仰耦合误差Fig.4 Azimuth-pitch coupling error of turntable
由图4可以看出,转台±20°转动过程中,方位俯仰角度的耦合误差最大能够达到1.2°,这个角度误差对于雷达系统来说是不能接受的,因此必须予以消除。
4.3 消除转台误差后的仿真
按照第2节和第3节的方法消除转台安装误差和耦合误差后,仿真结果如图5所示。
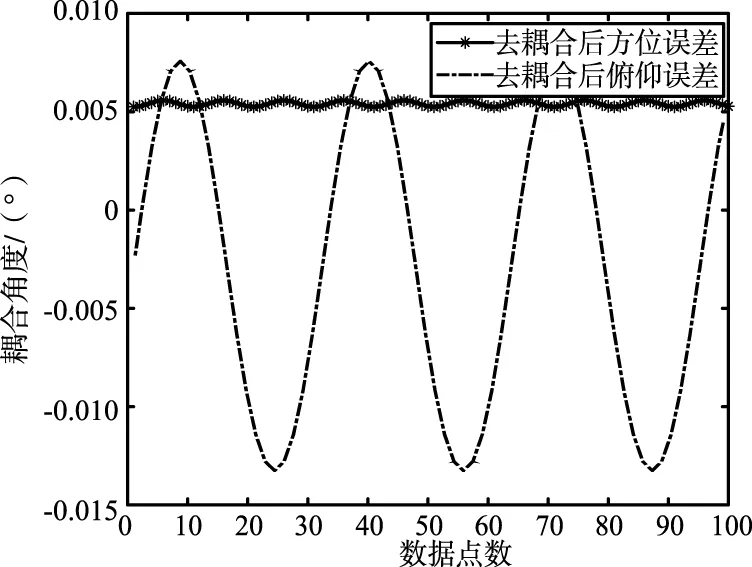
图5 去掉安装误差和耦合误差后的测角误差Fig.5 Angle measurement error after removal of installation error and coupling error
从图5可以看出,消除耦合误差后,由转台带来的额外的测角误差大大减少。可见本转台角度测量误差校正算法的有效性。在实际测量过程中,可以按照表1所示方法统计雷达测向误差,进而可以对照转台校正和不校正之间的效果。
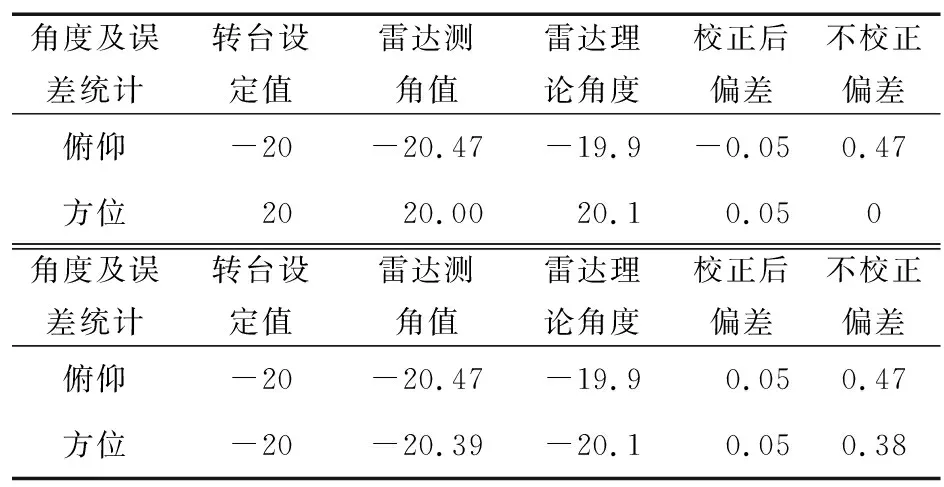
表1 典型目标角度处雷达测角精度统计表
由表1可以看出,按照本文修正算法能够将转台安装误差及耦合误差修正到0.1°范围内,能够极大地提高转台系统角度辅助测量的准确性。
5 结束语
针对转台测量系统的安装误差和耦合角度误差问题,利用主动雷达测角精度高的优点,在主动稳定跟踪的情况下,分别转动转台和移动目标,可获得雷达系统天线回转中心和转台回转中心的距离和角度偏移量。在此基础上推导了转台方位俯仰角度之间的耦合关系。最后给出了雷达转台系统角度误差校正算法的评价方法。仿真及实测结果表明,本算法能够有效地消除转台系统的安装误差及耦合误差,能够极大地提高雷达系统角度测量误差的可信度。本算法原理简单,计算量小,具有较强的工程实现意义。

