双曲线标准方程的推导及发现

杨永刚，陈红霞

（南充市高坪中学，四川 南充 637100）

文[1][2]是关于椭圆标准方程的推导及其发现、领悟的，其实双曲线的标准方程也可采用其它的方法来化简.在推导双曲线的标准方程时，大多数教师都会采用教材[3]中的推导过程（即方法1，后文所说教材、教科书均指[3]），有时教师会提一下直接平方会更复杂一点，并顺便否定其他的推导过程.本文采用五种方法来推导双曲线的标准方程，并试着沿教材编写者的意图来分析这样处理教材的原因.

1 双曲线标准方程的推导

2 启示与发现

仅从运算角度看，教材采用方法1的优势并不是很明显，那么教材这样处理的意义何在？通过笔者的教学，有以下发现.

2.1 (教材选修2-1)第55页探究

题目：点A、B的坐标分别是(-5,0),(5,0)，直线AM,BM相交于点M,且它们斜率之积是，求点M的轨迹方程.

分析：设点M的坐标(x,y)，那么直线AM,BM的斜率就可以表示成x,y的式子,由于它们斜率之积是，因此可以建立x,y之间的关系式，得出M的轨迹方程.启示与发现：

从中可以看出，双曲线也可以描述为平面内到两定点(-a,0),(a,0)(不包括这两点)的连线斜率的积为定正值的点的轨迹.

2.2 (教材选修2-1)第55页例5探究

题目：点M(x,y)到定点F(5,0)的距离和它到定直线的距离的比是常数，求点M的轨迹.

化简得：9x2-16y2=144，即

所以点M的轨迹就是实轴、虚轴长分别为8和6的双曲线.

启示与发现：

将③式变形为：

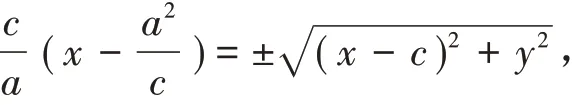
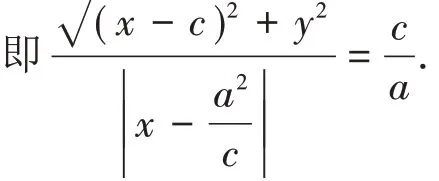
3 结语

方法4在数学史上采用得并不多，现在大多数人根本不熟悉，尽管在推导过程中还得到了焦半径公式：⑧式.方法5巧妙的利用了平方，从而避免了出现根式，再利用作差，就很简单得出了双曲线的标准方程，对学生来说也会觉得自然，在课堂上可以介绍给学生.

不同结构的数学式子具有不同的数学内涵，代表着不同的几何意义，但它们表示同一图形——双曲线.采用方法1不仅让学生得到了双曲线的标准方程，还理解了双曲线的不同描述，教学生完整的了解双曲线标准方程的含义，对双曲线各种表述留下较为深刻的印象，这样也对双曲线的领悟更深刻.反过来，这也使得单调、繁琐的运算过程变得生动而有活力，为双曲线方程的灵活运用打下了坚实基础.更重要的是让学生明白，变的是形式，不变的是本质这一科学道理[4].