非合作通信中一种高精度载频估计算法*
吴世鹏,孙 浩
(杭州电子科技大学,浙江 杭州 310018)
0 引言
在电子对抗侦察领域,由于通信方式为非合作通信,接收方并不能像合作通信那样获取信号的各种先验信息。因此,要想对信号做进一步的处理必须首先估计出信号的各种参数。载频估计是其中非常重要的一部分,载频估计的精确度对后续的信号处理有着重要的影响。
目前对于载频估计的研究主要分为时域与频域两大类。文献[1]根据载频与载波周期之间的关系,通过统计一定时间内信号过零点次数估计载波周期,进而估计出信号载频。该方法复杂度低,但是容易受到噪声的影响,在低信噪比下估计性能较差。文献[2]提出一种频率居中法估计载频的方法,根据信号的频谱信息估计载频,该算法实现简单但同样易受噪声的影响。文献[3-4]提出了基于Welch功率谱与高斯拟合平滑功率谱的载频估计方法,利用平滑后的功率谱代替信号的频谱。该方法有效降低了噪声对载频估计的影响,但是只适用于频谱对称性较好的信号。文献[5]提出将频偏估计扩展到载频估计中,利用估计出的频偏对载频估计结果进行补偿,但所提频偏估计算法只适用于PSK信号。文献[6]提出一种利用最大似然估计中的自相关函数估计频偏的算法,可以快速高效地估计出载波频偏,但是由于需要发送导频序列,因此并不适用于非合作通信中。文献[7]提出一种非数据辅助(Non-Data-Aided,NDA)频偏估计算法,利用M次方运算去除调制信息估计频率偏移的方法。该方法有效提升了载频估计的精度,但是需要预先知道信号的调制类型。
本文提出一种多级估计的载频盲估计算法。首先利用一种改进的频率居中法粗估计信号的载频,然后利用文献[8]提出的码元速率估计方法估计出信号的码元速率,之后把载频估计问题转化为频偏估计问题。根据两倍波特率采样点间包含信号频偏信息的特性提取信号频偏,最后将载频粗估计值与频偏估计值相加即可得到精确的载频估计值。该方法无需知道信号的调制类型,且在低信噪比情况下仍能保持良好的估计精度。
1 信号模型
假设接收到的信号可表示为:

式中,s(t)为经过载频调制后的信号,I(t)为基带调制信号的同相分量,Q(t)为基带调制信号的正交分量,其具体表达式如式(3)与式(4)所示,fc为载波频率,n(t)是均值为零的复数高斯白噪声。


式中,sn为第n个符号周期发射的符号,g(t)表示脉冲成形滤波器的冲激响应,T代表符号周期,fn表示基带信号频率。
2 载频粗估计
对接收到的信号首先采用频率居中法粗估计载频,其原理就是利用线性调制信号功率谱关于载频对称的特性将接收信号的频谱的中心频率作为载频的估计值,具体表达式如下:

式中,R(i)为对信号r(t)进行傅立叶变换后的频谱序列。该算法复杂度低,易于实现,但是在低信噪比情况下,信号功率谱受噪声影响导致两端拖尾部分幅值增加明显,从而引起载频估计精度不足,并且该算法只适用于频谱对称性较好的信号,对于频谱对称性较差的信号估计效果不佳。因此,如何消除噪声的影响以及选取对称性较好的数据是载频估计首先要解决的问题。
Welch功率谱是对功率谱直接估计法的改进,通过分段计算功率谱的方法来平滑功率谱[9],降低噪声对估计结果的影响。具体实现过程如下:首先,将长度为N的接收信号分割为每段长度为M的K段,即N=KM,每段之间允许有数据重叠;其次,将分割得到的每段数据加窗(如矩形窗或布莱克曼窗),然后根据周期图法计算每段数据的功率谱;最后,将每段数据的周期图功率谱相加取平均即为所求。公式表示为:

式中,w(n)为窗函数,U为归一化因子,表达式为:

以QPSK信号为例,在-5 dB信噪比情况下,信号的两种功率谱估计结果如图1所示。
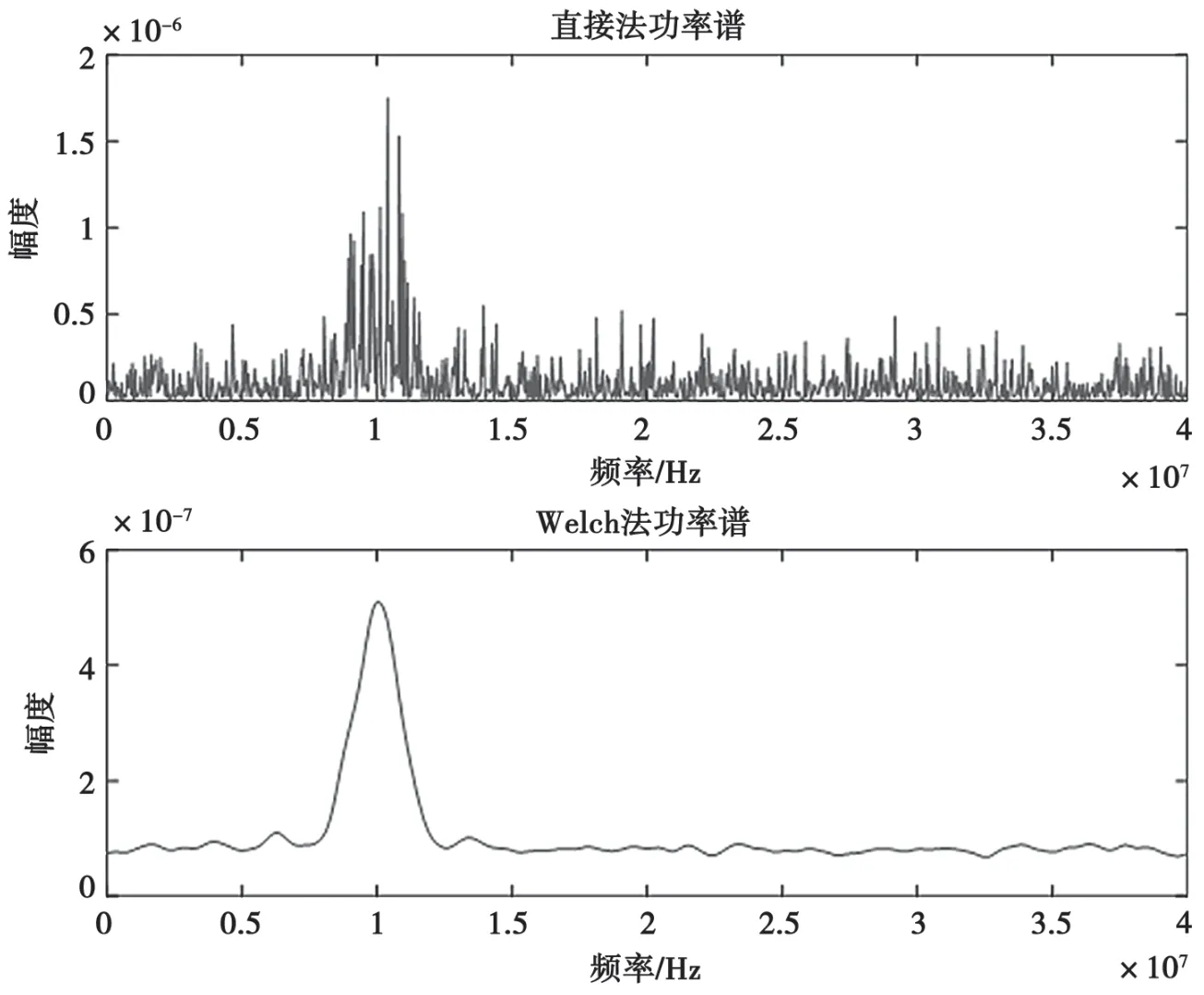
图1 信号的直接法功率谱与Welch法功率谱
从图1可以看出,原始信号的周期图法功率谱由于受到噪声的影响相邻频点之间的幅度波动较大,增加了信号中心频率的估计难度;信号的Welch功率谱相比于周期图法功率谱有效地去除了相邻频率间隔之间的幅度跳变点,得到了更为平滑的功率谱,其平滑效果与信号的分段数以及每段数据的重叠率有关。因此,通过信号的Welch功率谱可以更为准确地估计出信号的中心频率。
从图1同样可以注意到信号功率谱较强部分主要集中在峰值附近,因此可以通过提取信号功率谱较强部分后再利用频率居中法进行载频估计,这样可以确保进行载频估计时的功率谱数据有良好的对称性,且有效去除了功率谱两端拖尾对载频估计结果的影响,进一步改善在低信噪比情况下的估计性能,使最终的估计结果更加靠近理论值。提取信号功率谱较强分量时可以通过计算功率谱的均值与标准差的和设置门限,只保留超出门限部分。
3 频偏估计
由上述方法得到的载频估计结果是粗略的,并不能满足对信号进行后续处理的载频精度要求,因此,对载频进行进一步的精估计是有必要的。将接收信号r(t)乘以得到:

现有的频偏估计算法分为数据辅助频偏估计与非数据辅助频偏估计,但是由于非合作通信中无数据辅助特性,因此在频偏估计时只能选用非数据辅助的频偏估计。目前针对非数据辅助的频偏估计主要是通过对接收信号进行M次方非线性运算的方式来消除信号的调制信息,之后根据式(10)估计信号的频偏[10]。

式中,ωc=2π∆fT。由式(10)可以看出,要想估计出信号的频偏,必须先识别出信号的调制类型来确定M的值,这无疑增加了算法的复杂度,同时算法的最终估计精度也因此受到信号识别正确率的影响。
由文献[11]可知,信号的统计信息中包含着信号的频偏信息,因此考虑利用信号的统计信息来估计信号的频偏。对式(9)进行采样,采样周期设置为T/2,即在一个符号周期内采两个点,得到的两个样点之间存在着相关性,其中包含着信号的频偏信息,可据此估计出信号的频偏。经过T/2采样后的信号如式(11)所示:

由式(12)可以进一步推导出信号的频偏估计公式:

由式(13)得到的频偏估计值∆f并不是一个无偏估计量,而是受到噪声的影响在均值附近浮动。为了得到更为准确的估计值,可以对信号采用均值滤波的方法提高估计精度。设第i次的频偏估计结果为∆fi,则:

从算法的推导过程可以看出,最终的频偏估计结果对信号先验知识的要求较小,可以在缺少信号先验信息的情况下实现频偏的盲估计。此外,由于先对信号的载频进行了粗估计,使得信号的频偏落在较小的范围内,因此消除了算法频偏估计范围的限制。最后将频偏估计值与第2节的载频粗估计值相加即可得到信号载频精估计结果。
4 仿真实验与结果分析
对本算法进行MATLAB仿真,比较频率居中法与频偏补偿后的载频估计效果,并通过载频归一化误差均值来评价算法性能。定义如下:
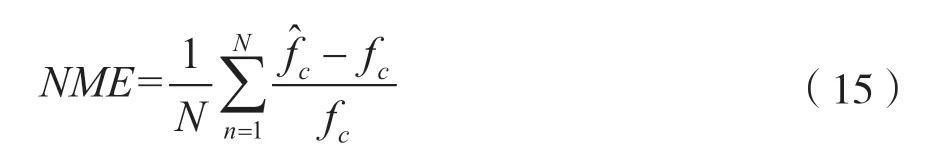
仿真时,为验证算法的普适性,选用2ASK、QPSK与16QAM三种数字调制信号进行仿真。信号的波特率设置为2.5 MBaud/s,载波频率为10 MHz,采样频率为40 MHz。信号噪声背景为高斯白噪声,即信号传输信道为AWGN信道,信噪比范围设置为-5~15 dB。在不同信噪比下分别进行100次蒙特卡洛仿真实验,得到3种信号在两种算法下的误差均值曲线分别如图2、图3、图4所示。

图2 2ASK载频估计误差均值曲线
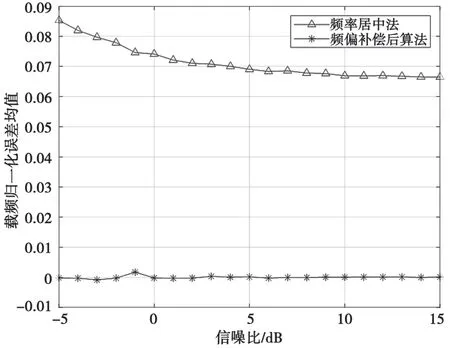
图3 QPSK信号载频估计误差均值曲线

图4 16QAM信号载频估计误差均值曲线
从仿真结果可以看出,随着信噪比的降低,频率居中法估计的载频估计精度下降较快,在信噪比高于10 dB时其载频估计误差曲线趋于平缓,最终的载频估计结果与理论值相比仍有一定的误差,这再次证明了对载频粗估计值进行补偿的必要性。从最终的结果可以看出经过频偏补偿的载频估计算法相比于频率居中法性能有了较大的提升,载频估计结果更加接近于理论值,且在低信噪比情况下仍有较高的载频估计精度,验证了算法的抗噪性能良好。此外,仿真结果表明该算法对于ASK、PSK与QAM信号都有良好的估计性能。
5 结语
针对电子对抗侦察等非合作通信环境,提出一种无需信号先验信息的载频估计算法。利用信号的功率谱对信号载频粗估计,之后利用信号的自相关函数提取载波频偏信息,并对载频粗估计结果进行补偿,进一步得到载频精确估计结果。MATLAB仿真结果表明,该算法可以实现对ASK、PSK以及QAM信号载频的精确估计,且在低信噪比情况下仍能保持良好的估计性能。该算法复杂度低,易于实现,适用于电子对抗侦察等非合作通信系统中。

