动静结合—初中数学“二次函数”教学研究

黄启

摘要：在整个初中数学教学中，二次函数可以说是占据数学半壁江山，它渗透了数学的数形思想，可以培养学生的空间思维能力，以及识图与观察能力，对培养逻辑推理、数学建模、数学抽象、直观想象等综合素养具有积极的影响。而动静结合法在二次函数教学中的应用，可以培养学生的动手、动脑能力，还可以提高解题技巧，创新教学环境。为此，本文分析了初中数学二次函数的特点，解读了动静结合思想在二次函数教学中的教学技巧和学习路径。

关键词：动静结合;初中数学;二次函数

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2021）04-085

在初中数学新课标中指出：在教学中，教师要善于创造教学情境，让静止的、抽象的知识点动起来，从而培养学生的观察能力、思维能力、推理能力。因此，在初中二次函数教学中，为提高问题解决质量，增强二次函数的教学效率，在教学时，要结合动、静之间的关系，在动静渗透中，促进对函数知识的理解和掌握。本文分析了初中数学二次函数的特点，解读了动静结合思想在二次函数教学中的教学技巧和学习路径。

一、初中数学二次函数的特点

1.识图与观察

在初中二次函数教学中，不论是理解概念，还是解析函数问题，观察函数图像都是分析理论的前提，通过图形的探究和观察，更加有助于提高学生对函数知识点的理解，提高自己的数学抽象素养和直观想象素养。因此，在动静结合教学法渗透的过程中，要结合识图，在动眼、动脑，观察的过程，让学生做学习的主人，促进深度学习。

2.动手与推理

在解析二次函数有关问题的时候，正确作图、精准作图、高效作图是前提。旨在通过题意分析，在动脑的过程中，结合动手实践，完成问题推理，建立解题模型。因此，在渗透动静结合法的时候，要结合动手与推理的特点，让学生勤动手，在多维作图的过程中，借助数、形、动、静等思想，优化解题思路，从而提高数学建模、直观想象、逻辑推理等综合素养。

3.理论与应用

数学与我们日常生活有着紧密地联系，在教学函数的过程中，其根本目的是达到学以致用，结合理论与应用的特点，让静止的知识点得以实践，从而发挥数学自身的价值。因此，在动静结合教学中，要依据理论与应用的特点，通过经典问题引导，结合实践应用问题，促进动态思维发展，让动、静得到有机结合，提高函数教学质量。

二、动静结合思想在二次函数教学中的教学技巧

1.以激活思维为入手点

在初中二次函数教学中，很多学生认为这是一项枯燥乏味的学习过程，不仅仅因为知识难度的增设，更是因为知识内容的复杂、零碎。在学习过程中，既有抽象的理论定义概念，同时也具有数形分析，还有函数与方程关系的探究等，要想全面了解、掌握这一知识内容，要求学生必须具有较强的思维能力和学习能力。因此，为提高数学主动学习能力，在教学的时候，可以以激活思维为入手点，结合学生的学习兴趣为辅助，在动静结合中，通过真实生活情境的打造促使函数学习更加灵活多变。这样既可以使其认识函数的应用价值，又可以丰富教材内容。

2.以实践应用为出发点

动静结合教学思想在初中二次函数教学中的应用，旨在通过动，提高对有关静问题的思考和认识，在动手、动脑的过程中，使其能够应用函数知识解决相关问題。为此，在学习的时候，为提高二次函数教学质量，可以通过实践与应用的结合为辅助，在实践探索、切实体验的过程中，使其应用这一静止的知识点服务生活实际，从而达到学以致用的教学目的，加深对二次函数知识的印象。这样既可以培养学生的空间思维能力，又可以将函数与社会发展和生活实际进行有机关联，让学生善于利用学，提高自身的能力。

三、动静结合思想在二次函数教学中的教学路径

1.依据静态抽象概念，打造动态生活情境

二次函数概念具有抽象性的特点，但是要想让学生学好二次函数，概念理解和掌握是基础。在传统教学中，对于概念都是以教师讲为主，学生靠死记硬背记忆，完全不理解函数定义内涵，动静结合思想下倡导学生理解记忆，灵活运用。因此，为激活课堂教学的趣味性，提高学生学习能力和理解能力，在解析函数概念的时候，可以打造动态的生活情境，在直观化、动态化展示的过程中，化解抽象内涵，培养动静结合学习思想。

例如，在教学解析“二次函数的含义和概念”数学内容时，为让学生理解二次函数“y=ax2+bx+c（a，b，c是常数，a≠0）”的函数概念，在学习的时候，可以设计以下动态情境，如：为小动物建筑娱乐空间，已知要用64米长的围墙围成长方形的园区饲养小动物，使其能够在园区内自由活动，那么，对于长方形的长和宽，应该怎样设计，才能使得小动物的活动范围最大？假如设长方形的长为x米，长方形的宽应该为多少米，设面积为y，则变量y与x之间的函数关系又应该怎样表示？让学生动脑思考，在创造动态情境的过程中，引导其复习正比例函数、以及函数关系表达式，随后让学生自主猜测长方形面积与边长的表达式是什么函数？由此引出二次函数有关知识内容，让学生利用已学得到的函数知识求解长方形的最大面积，在创造动态情境，引导其动脑探究的过程中，渗透动静结合思想，化解抽象函数概念，从而培养自主探究学习能力，以及动脑学习习惯。

2.利用动手作图分析，深化函数图形认识

在教学二次函数数学知识点的时候，图形图像的分析认识是学习、解析函数问题的关键，其中y=a（x-h）2+k与y=ax2图像关系的认识作为教学的重点，为培养学生的归纳能力，培养逻辑推理数学核心素养，在学习的时候，可以通过动手作图分析为辅助，在亲身经历、作图分析的过程中，为学生研究函数图像指明思路方法，从而深化对二次函数图形的认识。

例如，在学习y=a（x-h）2+k与y=ax2图像关系数学内容时，教师可以让学生在同一个坐标系中，通过动手操作绘制“y=2x2、y=2（x-1）2、y=2（x+1）2，y=（x-1）2-1和y=2（x-1）2+1”等函数图像，观察这几个函数图像的开口方向、顶点、对称轴、增减性，在动手探究绘制图像的过程中，结合几个函数图像，分析y=a（x-h）2+k与y=ax2图像的区别和联系，利用观念系统中已经有的关于点和直线平移的机制，引导学生动眼观察顶点、对称轴的平移路径，在观察函数图像平移路径的过程中，培养归纳能力，让学生动手、动脑思考分析y=a（x-h）2+k与y=ax2图像关系，从而为学生设计以下动手、动脑分析问题，如：

①二次函数y=a（x-h）2+k的图像是什么形状？

②绘制y=a（x-h）2+k与y=ax2图像对比图，分析其有什么区别和联系？

③他们之间是经过怎样变化得到的？由y=ax2的图像性质，怎样说明y=a（x+m）2+k的性质

在动手作图、问题层层引导的过程中，深化对函数图形的认识，让学生在学习探究图像性质的时候，有一个良好的学习习惯，使其学会运用动手作图，对比分析的方法，在对比中，认识图形图像，提高自己的空间思维能力，增强动手探究学习能力。这样既可以渗透动静结合的思想观，又可以使其形成动静结合的学习习惯，在动手、动脑、动眼的过程中，培养细致地观察能力和科学的分析能力，从而提高数学逻辑推理核心素养。

3.通过经典知识引导，促进函数实践应用

函数与我们日常生活有着很深的关联，为让学生认识到函数的应用价值，端正学习态度，教师可以走出课堂，走进生活，在切实实践、认识社会、了解生活的过程中，结合实时数据，以及函数有关问题，引导其利用所学知识服务生活，从而达到学以致用的教学目的。

例如，在解决有关函数问题的时候，对于课本上的习题以及卷子中的专题练习想必学生能够信手拈来，根本不能满足学生的学习发展需求，那么，在学习的时候，可以开展实践活动，让学生动身参与到社会生活中，为其发放生活调查表，让学生带着发现的眼光，调查生活中有关函数的知识内容，如：

生：新冠肺炎以来，医用防护服非常紧缺，为防控一线助力，根据切实调查发现，防护服的日常销售量和日销售利润、销售单件成函数关系比例发展。

在此过程中，教师可以结合有关函数经典知识内容为辅助，依据学生动身实践调查所得有关函数关系的信息为核心，导出以下函数应用问题，如：

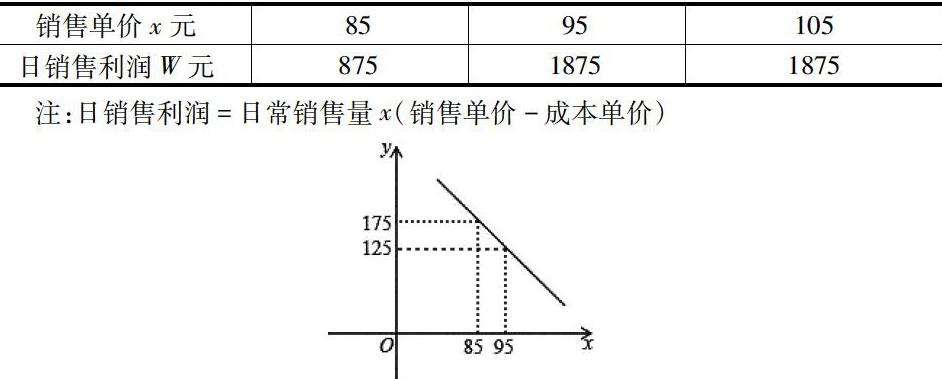
武汉新冠肺炎发生以来，某医疗公司积极复工，加班加点生产医用防护服，为防控一线助力，以下是该公司以往的市场调查，发现该公司防护服的日销售量y套与销售单价x元之间满足一次函数关系，如图所示，关于日销售利润W元和销售单价x元的几组对应值，如：

①求y与x函数解析式

②根据函数图像和表格所提供的信息填空：

该公司生产的防护服的成本单价是 元，当销售单价x= 元时，日销售利润W最大，最大值是 元

③该公司复工以后，在政府部门帮助下，原材料采购成本比以往有了下降，平均起来，每生产一套防护服，成本比以前下降5元，该公司计划开展科技创新，以降低该产品的成本，如果在今后的销售中，日销售量与销售单价仍然存在①中的关系，若想实现销售单价为90元，日销售利润不低于3750元的销售目标，该产品的成本单价应该不超过多少元？

在解决这一问题的时候，其根本点，在于通过实践调查，在动的过程中，让学生认识函数的应用，使其这一静止的知识内容以动态发展的形式呈现，从而激活解题兴趣。在解决这一问题的时候，可以联系与疫情有关内容，让学生先说一说此次疫情的影响，在激活交流沟通兴趣的过程中，根据题意运用y=kx+b解析问题①，在解题②的时候，引导其利用二次函数的性质，通过动手绘制图像、结合题意、性质特点等进行问题解决，在问题③中通过带入思考分析。通过经典知识的动态应用，达到学以致用教学目的，提高教学质量。

4.借助动态图像分析，提高函数解题分析力

在学习二次函数的过程中，作图、分析图是非常关键的一步，同时也是规划解题路径的有效途径。为此，为渗透动静结合思想，提高二次函数解题质量，可以通过借助动态图像对比的方法，在数形结合，动手探究、动脑思考的过程中，培养解题策略，提高解题效果。

例如，在解析这一函数问题，如：若二次函数y=x2+（1-2m）x-m+5的图像不经过第三象限，则实数m的取值范围是？

在解析这一函数问题的时候，结合y=x2+（1-2m）x-m+5形式，以及题意提示“不经过第三象限”，可以引导学生动手繪制二次函数图像，在动态图像绘制的过程中，利用数形对比，进行问题思考，如：

根据动手图像制作，结合题意提示，可以让学生根据对称轴的位置进行分类讨论，如：

①若对称轴在y轴左侧，则应该满足△≤0，或者ymin≤0

②若对称轴在y轴上，或者y轴右侧，则根据图像所示，y（0）≥0

通过动手制图分析，以及分类讨论法的应用，在动手、动嘴的过程中，让学生自主规划解题路径，让学生做学习的主人，针对此题进行教学讲解，提高解题能力和解题质量，然后让其他同学根据讲解进行点评。通过动静结合思想的渗透，在教学方法优化的过程中，提高课堂教学质量，培养数学建模、直观想象、数学分析等核心素养。

综上所述，动静结合思想在初中二次函数教学中的应用，教师要认识函数学习的围绕特点，探究动静结合思想在教学中的技巧，从而根据特点和技巧制定教学策略，让学生在动静结合思想中掌握有关函数的知识点，达到学以致用。通过动态情境引导、动手作图分析、动身体验应用、动嘴沟通交流等，使其理解函数抽象概念，提高对函数图像性质、函数应用价值等内容的理解和掌握，提高二次函数教学质量。

参考文献：

[1]李娜.初中数学中“二次函数”的教学策略[J].教育艺术，2020（9）：68.

[2]王绪新.初中数学中“二次函数”的教学策略[J].数理化解题研究，2020（26）：36-37.

[3]黄致和.谈初中数学二次函数的教学[J].当代家庭教育，2020（25）：110-111.

[4]代娇春.初中数学中“二次函数”的教学策略探讨[J].新课程，2020（37）：94.

（作者单位：广东省珠海市斗门区乾务镇五山初级中学，广东 珠海 519000）