探究数形结合思想在高中数学教学中的应用

汪元生

在高中阶段，学生遇到的函数问题越来越多，对于此类抽象的问题，有时候学生并不能直接理解，这时候就需要教师采取不同的教学方法，帮助学生简化问题，让学生能够以更简单的方式掌握教学内容，进而达到对知识的理解。

一、数形结合的意义

数形结合，从字面意思来看，就是将数和图形进行结合。说得再仔细一些，在数学学习的过程中，数和图形是学生接触的最多的两种数学形式，而且在大多数数学题目中，学生能够将这两种形式进行相互转换，从而得到相应的关系式或者条件。在这样的情况下，学生就能够将之前比较抽象的东西具象化，从而得到清晰的解题思路，更好地解答题目。

二、数形结合在高中数学学习中的意义

在数学学习的过程中，教师应当致力于培养学生的数学思维。在数学思维中，就包括对学生形象思维的培养。通过对正确的学习方法的培养，能够有效地提升学生学习的积极性，提升学生的学习兴趣。数学学科是一门包含着数和图形的较为抽象的学科，因此在学习的过程中，学生难免会产生一种不理解的思维，有时甚至会因为某些混乱的知识点而导致对该科目的厌学情绪。因此，要想让学生形成一种正确的学习方法，激发学生对学习该科目的积极性，教师就应当较好地把握数形结合这种方法。例如，在高中必修一中会接触到函数部分的知识，在这部分知识的学习过程中，教师可以通过将函数式和函数图像相结合，让学生看函数的自变量和因变量是如何变化的，明白这种图像的变化趋势，这样学生就能够更加直观地了解其中的变化规律，从而加深对函数概念的理解。此外，随着现代科学技术的发展，学生能够通过现代科技进行学习，这样也能够提升学生的学习兴趣，让学生在课堂中将更多的注意力集中在课堂上，从而提高听课效率。

三、数形结合在高中数学学习中的应用

（一）数形结合思维在三角函数中的应用

在高一阶段，学生将会接触到函数，但是这种函数又和初中阶段学到的函数有着较大的区别，而这种函数思维又将贯穿高中三年的数学学习。这时教师就可以采用数形结合的方式，避免只通过枯燥、抽象的概念来向学生传递这一类型的重要知识点。例如，在高一阶段学生会接触到一种新型的函数，即三角函数。对于这种新型的知识点，学生可能会感到陌生甚至排斥，而且在三角函数中存在着多种类型，如正弦函数、余弦函数、正切函数等。这几种函数在图像上有相似点和不同点，在考试中也会将这几种函数交叉考查。所以在高一阶段对这些知识点的教授过程中，教师可以充分利用数形结合的方法进行讲授，这样能够很大程度上提高学生的理解效率，达到事半功倍的效果。在这种函数中，图形是非常经典的一个知识点，对三角函数来说，存在着单调性、奇偶性以及函数的区间，对于这些知识点，学生仅仅依靠对性质的研读很难理解，但是加上图像，学生就能很快理解这几种性质的变化，并且能够在较短的时间内记住。在三角函数的学习中，图像和性质是相辅相成的，只要会画图，就能够分辨出其他的相关性质；只要知道相关的性质，便能够作出具有该性质的图形。

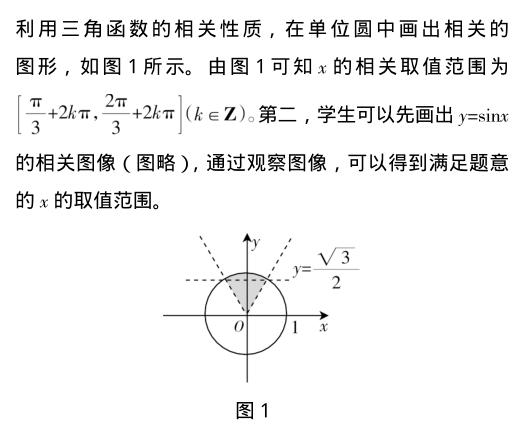
通过上述问题，可以得知在解决三角函数的相关问题时，可以让学生通过对三角函数的性质的分析，将代数问题通过图形的方式求解，从而能够迅速得出答案。这样不仅能够让学生加深对三角函数的理解，还能够探索出一类问题的不同解法，发散思维，培养对问题的不同思考角度。

（二）数形结合思维在抽象函数学习中的应用

在高中阶段，学生还会接触到抽象函数的学习。在这个阶段的相关学习中，为了让学生对相关知识更加容易理解，教师可以采用数形结合的方法进行教学。例如，我们在高中阶段会讲到奇函数和偶函数的相关性质，其中有很多知识点单凭口头描述是很难想象的，这些知识点比较抽象，不容易理解。例如，y=f（x）是一个偶函数，在区间（-∞，0）上为减函数，并且f（2）≤f（a），求出a的实际取值范围。在遇到这类问题时，如果只是单纯利用函数性质进行推导，会增加很多不必要的计算量，导致计算过程复杂化，增加解题的时间。如果学生学会利用数形结合的方法，在解决这个问题时就会容易很多。通过题目中给出的条件，学生可以画出相关的图像，如图2。

通过对这个图形的观察，很容易就能看出这个函数是偶函数，并且能够通过图像对条件中a 的取值范围做出解答。因此，在解决这一类型的抽象函数问题时，如果采用数形结合的方法，将函数图像画出来，就能够结合相关的性质，很快求出问题的答案。

对于数形结合思维的运用，可以引导学生利用不同的思维方式思考问题，将思考问题的过程由静止的转化为动态的，然后用动态的思维过程来探究相关问题的解法，这样才能够掌握一类问题的本质，从而达到举一反三的效果。教师在培养这种思维方式的时候，其实也是培养学生分析问题和解决问题的能力，让学生掌握透过现象看本质的方法。

（三）数形结合思维在圆锥曲线学习中的应用

在高中阶段圆锥曲线的学习中，数形结合方法也是十分重要的。例如，教师在讲授圆锥曲线的相关定义时，可以从数和形两个方面入手对定义进行讲解，从而加深学生对曲线和量之间的关系的认识。

从题干的相关描述中，学生可以确定椭圆的相关信息，因此函数中a、b的值也比较容易得到，此外，学生可以利用图像得到一些没有给出的条件，这里就体现了图像的简便性，能够很容易得出题干中没有给出的相关条件。再将其代入椭圆中，就能够较为简便地解出题目的结果。

在高中阶段会遇到各种数学问题，其中不仅包括函数问题及图形问题，还包括其他一系列的几何问题。对这些问题的探讨会花费学生大量的时间和精力，而掌握正确的学习方法则是节省时间的一大利器。因此，教师应当在教学的过程中注意总结典型例题，将可能出现的问题进行总结，引导学生采用不同的思维模式思考问题。除此之外，教师应当引导学生利用数形结合的方法进行思考，将数学性质和图形结合起来，节省解题的时间，从而提升学生的做题速度，让学生能够更快、更好地學习相关知识。