Some Properties on the b-chromatic Number of Special Graphs

WANG Guo-xing CAO Xiao-jun

(1- Gansu Silk Road Economic Research Institute, Lanzhou University of Finance and Economics, Lanzhou 730020; 2- College of Information Engineering,Lanzhou University of Finance and Economics, Lanzhou 730020)

Abstract: Graph coloring is one of the most hot issues in graph theory and has important applications in many fields. For a connected graph G, we use χ(G) and φ(G) to denote the chromatic number and b-chromatic number of G, respectively. Let R, S be two connected graphs. Then G is said to be {R,S}-free if G does not contain R and S as induced subgraphs. In this paper, we prove that for any connected graphs R and S of order at least 4, every connected (2-edge-connected or 2-connected){R,S}-free graph G implies χ(G) = φ(G) if and only if {R,S} ≼{P5,Z1}, where P5 is a path of order 5 and Z1 is the graph obtained by identifying one vertex of P2 and one vertex of a triangle. Besides, we give the lower bound of b-chromatic numbers of two special classes of interlacing graphs IGn,2 and IGn,3.

Keywords: chromatic number; b-chromatic number; induced subgraph; interlacing graph

1 Introduction

Graph coloring has a wide range of applications in many fields, such as computer science, network theory, social science, and more specific as, time tabling and scheduling, frequency assignment, register allocation, computer security, electronic banking,coding theory, communication network, logistics and so on[1]. Since customers have increased dramatically, it will yield a confliction between the increasing customers and the limited expansion of communication network resources. In order to solve the above problem, a series of distinct colorings of graphs have been proposed over the past two decades.

In fact,coloring of graphs has a direct relation with maximum and minimum graph parameters. But many maximum and minimum graph parameters have ‘minimum maximal’ and ‘maximum minimal’ counterparts, respectively. Much algorithmic activity has been focused on such parameters relating to domination, independence and irredundance. However, the implicit partial order throughout is that of set inclusion.Based on the above, Irving and Manlove[2]first introduced the concept ofb-chromatic number,that is,ab-coloring of a graphGis ak-proper coloring such that in every color class there is a vertex that has a neighbor in all of the remaining color classes, and theb-chromatic number ofG, denoted byχb(G), is the maximum integerksuch thatGadmits ab-coloring withkcolors. Since then theb-chromatic number has drawn quite some attention among the scientific community. Already Irving and Manlove[2]have proved that finding theb-chromatic number of any graph is anNP-hard problem, and also gave a polynomial-time algorithm for finding theb-chromatic number of trees.

All graphs considered in this paper are simple graphs. For the notation or terminology not defined here[3]. A graph is called trivial if it has only one vertex, nontrivial otherwise. LetGbe a connected graph. We useκ(G),κ′(G) andg(G) to denote the connectivity, edge connectivity and girth ofG, respectively. Letube a vertex ofGandSbe a subset ofV(G) (orE(G)). The induced subgraph ofGis denoted byG[S].We useNG(u) to denote the neighborhood anddG(u) to denote the degree ofu. The neighbors ofSinGis defined asNG(S) =∪x∈SNG(x)SandNG[S] =NG(S)∪S.DefineNT(S)=NG(S)∩TforT ⊆V(G). Let

Vi(G)={u ∈V(G)|dG(u)=i}, V≥i(G)={u ∈V(G)|dG(u)≥i}.

IfF, Gare graphs, we writeF ⊆GifFis a subgraph ofGandF ∼=GifFandGare isomorphic. Forx,y ∈V(G) andH ⊆G, letE(u,H) ={uv ∈E(G)|v ∈V(H)},dG(x,y)=|E(P(x,y))|, whereP(x,y) is the shortest path betweenxandy,

dG(x,H)=min{dG(x,y):y ∈V(H)}, Ni(H)={x:dG(x,H)=i}.

LetHbe a set of connected graphs. A graphGis said to beH-free ifGdoes not containHas an induced subgraph for allH ∈H, and we call each graphHofHa forbidden subgraph. Especially, if{H}=H, then we simply say thatGisH-free and we callHa forbidden pair if|H|=2. For two setsH1andH2of connected graphs, we writeH1≼H2if for every graphH1inH1, there is a graphH2inH2such thatH1is an induced subgraph ofH2.

Ak-coloring of a graphGis a partition(V1,V2,··· ,Vk)ofV(G)such that{u,v}̸⊆Viifuv ∈E(G) for anyi ∈{1,2,··· ,k}. The minimum cardinalitykfor whichGhas ak-coloring is the chromatic numberχ(G) ofG. The vertexvi ∈Viis called theb-vertex if there is a vertexvj ∈Vjadjacent tovifor everyj ∈{1,2,··· ,k}{i}.

Theb-chromatic numberφ(G) is the largest numberkfor which there arek bverticesv1,v2,··· ,vksuch thatvi ∈Vifori ∈{1,2,··· ,k}in ak-coloring ofG. And such a coloring is called ab-coloring. The graphb-coloring is an interesting technique that can be applied to various domains and engineering application. For example, by using theb-coloring of graphs, Dekar in [4] proposed a self-learning scheme based on a new dynamic clustering of web services and Elghazelet alin [5] presented a new graphb-coloring framework for clustering heterogeneous objects into groups.

Thus,it is important to study some property onb-chromatic number. In this paper,we compareχ(G)andφ(G)of connected graphG. The more results aboutb-chromatic number see [6–10]. The following is the main result.

Theorem 1LetR, Sbe two connected graphs other than one of{P4,P3}. Then every connected(2-edge-connected or 2-connected){R,S}-free graphGimpliesχ(G)=φ(G) if and only if{R,S}≼{P5,Z1}.

2 The proof of Theorem 1

Let’s start with the following result.

Lemma 1Every connected{P5,Z1}-free graphGof order at least 6 either contains aKφ(G)as a subgraph orχ(G)=φ(G)≤3.

ProofColor the vertices ofGby aφ(G)-coloring(V1,V2,··· ,Vφ(G))such thatvi ∈Viis theb-vertex fori ∈{1,2,··· ,φ(G)}. We assume thatGdoes not containKφ(G)as its subgraph. Thenφ(G)≥3 andG[{v1,v2,··· ,vφ(G)}]Kφ(G), by symmetry,assumev1v2/∈E(G). Then there are two verticesu1∈V1andu2∈V2such that{u1v2,u2v1}⊆E(G). SinceGisP5-free, 2≤dG(v1,v2)≤3.

IfdG(v1,v2) = 3, then there is an edgexy ∈E(G) such that{xv1,yv2} ⊆E(G).Note that there is a vertexx′∈NG(v1){x}, {x′x,x′y}̸⊆E(G)sinceG[{x,x′,y,v2}]Z1, and thenx′x/∈E(G) sinceG[{v1,x,x′,y}]Z1, and hencex′y ∈E(G) sinceG[{x′,v1,x,y,v2}]P5. However, there are two verticesx0∈NG(v1)∩V3andy0∈NG(v2)∩V3such thatv1x0yv2y0is an induced path of order 5, a contradiction.

ThusdG(v1,v2)=2. There are three vertex sets:

X12=NG(v1)∩NG(v2), X1=NG(v1)X12, X2=NG(v2)X12,

such thatu1∈X2, u2∈X1. SinceG[{x,v1,v2,y}]Z1forx ∈X1∪X2, y ∈X12, E(X1∪X2,X12)=∅. ThenX1,X2andX12are three independent sets ofGsinceG[{xi,yi,vi,z}]Z1for{xi,yi} ⊆Xi, z ∈X12, i ∈{1,2}andG[{x,y,v1,u2}]Z1for{x,y} ⊆X12. Note that there is aC5⊆G. Thenχ(G) =φ(G) ifφ(G) = 3.We then assume thatφ(G)≥4. Then there is ab-vertexv3with colourk ̸= 1,2 which is not inX1∪X2∪X12ifφ(G)≥3 what’s more,G[X1∪X2]∼=K|X1|,|X2|sinceG[{x1,v1,x12,v2,x2}]P5for anyx1∈X1, x2∈X2, x12∈X12. Note that{v1v3,v2v3}∩E(G)=∅,by symmetry,{x1v3,x2v3}⊆E(G)for somex1∈X1, x2∈X2,and henceG[{x1,x2,v3,v1}]∼=Z1, a contradiction.

The proof of Theorem 1By Lemma 1, the proof of sufficiency clearly holds.It remains to show the necessity. We then consider the graphsG1,G2,··· ,G6depicted in Figure 1. Note that the graphG1is an even cycle with length at least 6,χ(G1)=2 andb(G1) = 3. The graphG2is obtained from a complete bipartite graphKn,nby deletingnmatching edges withχ(G2) = 2 andb(G2) =n. The graphG3is obtained from a complete graphKnand aP4such that each vertex inKnis adjacent to each end vertex ofP4withχ(G3)=n+1 andb(G3)=n+2.

Figure 1 Five classes of auxiliary graphs

G4is the graph withV(G4) ={v1,v2,··· ,v6}∪{x1,x2,··· ,xt}∪{y1}, E(G4) ={v1v5,v1v6,v2v3,v2v5,v3v6,v4v5,v4v6,v5v6}∪(=1{xiv1,xiv2,xiv4})∪{y1v1,y1v3,y1v4}.Thenχ(G4)=3 since there is a 3-coloring (V1,V2,V3):V1={v1,v4}, V2={v2,v6,y1}andV3={v3,v5,x1,··· ,xt}. Besidesb(G5)≥4 since there is a 4-coloring(V1,V2,V3,V4):V1={v1,v2},V2={v3,v4},V3={v5,y1},V4={v6,x1,··· ,xt}such thatv2,v3,v5,v6areb-vertices.

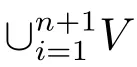
Thus each graph above contains at least one ofR, Sas an induced subgraph.Without loss of generality, we assume thatG1containsRas an induced subgraph.IfR=G1, note thatG2andG3areG1-free and have no common cycle,G2isK3-free andG3is{K1,3,P5}-free, then their maximal common induced subgraph isP4, a contradiction.

ThenR ∼=Pkfork ≥5. Note thatG2andG3areP6-free,k= 5. The graphsG3, G4, G5areP5-free, soSis a common induced subgraph of them. Besides,G3has only inducedK3andC5,G4is{C5,K4}-free andG5is (K4−e)-free, thenScontains exactly one triangle and their maximal common induced subgraph isZ1, and hence{R,S}≼{P5,Z1}.

3 The b-chromatic number on the subgraph of Kneser graphs

The Kneser graphKGn,kis the graph with vertex set corresponding tok-subsets of [n] ={1,2,··· ,n}, where two vertices are adjacent if the corresponding sets are disjoint.

Theorem 2[11]For fixedn ≥2, the Kneser graphGk=KGn,ksatisfies

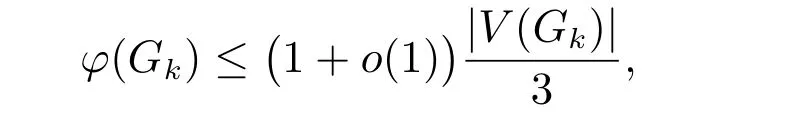
where theo(1) term tends to zero asktends to infinity.

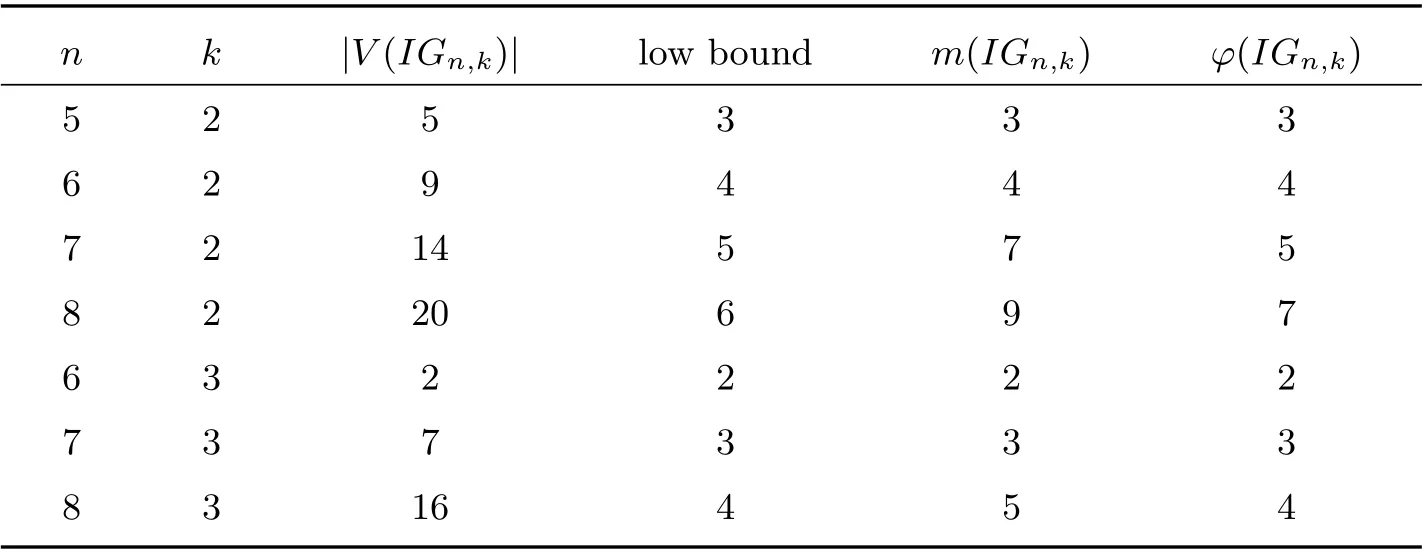
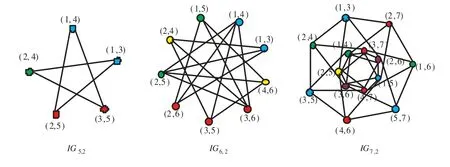
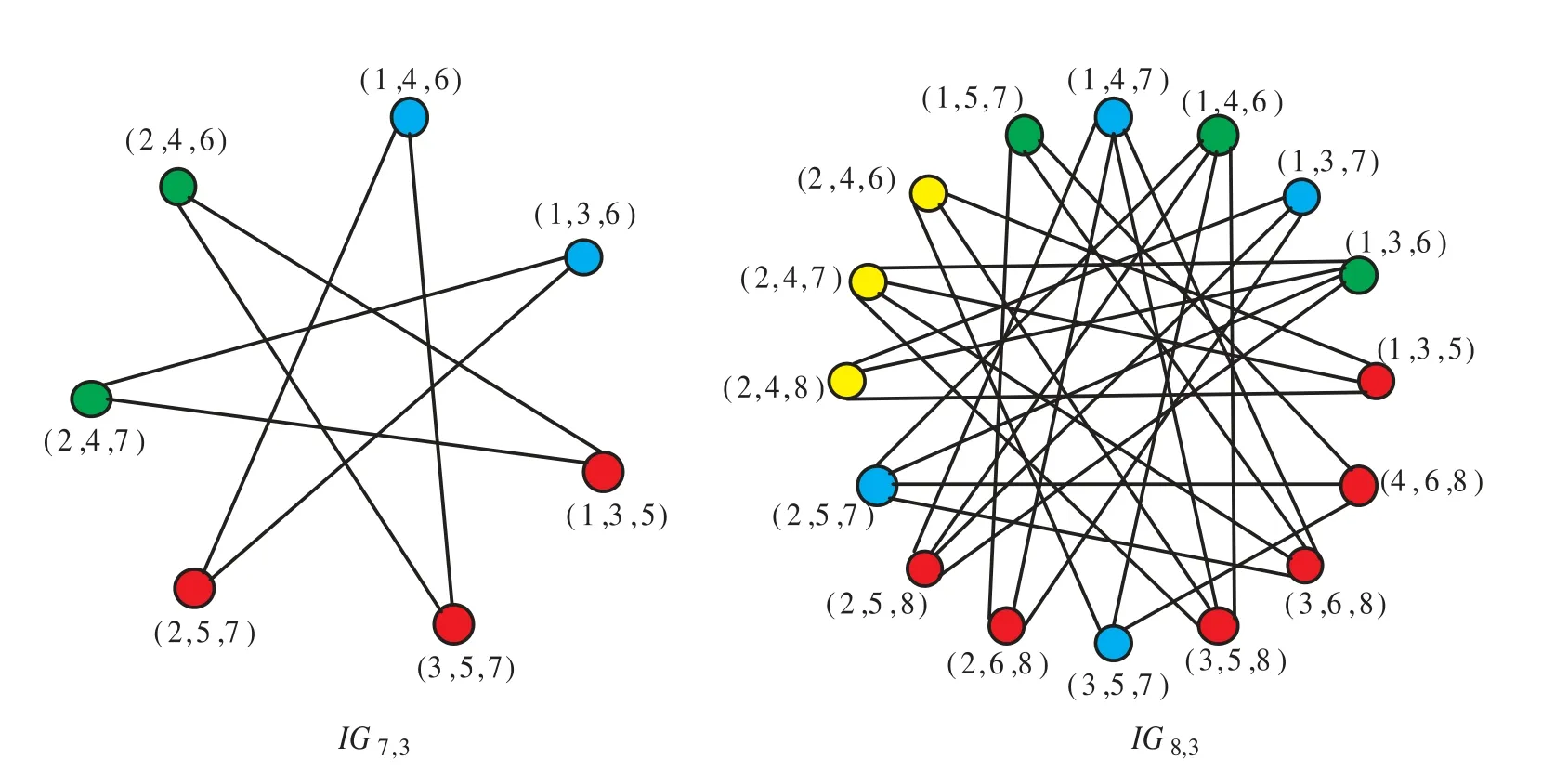
Other properties on Kneser graph, see[12,13]. We next consider a subgraph of the Kneser graph. The interlacing graphIGn,kis the graph with vertices corresponding tok-subsets of [n] that do not contain such pointsa, bsuch that|a −b|≤1, and edges betweenk-subsetsP={P1,P2,··· ,Pk}andQ={q1,q2,··· ,qk}with 1≤p1<···pk ≤nand 1≤q1<···

Note that for any integern ≥8,IGn,2[{1,4},{2,5},{3,7},{6,8}]∼=Z1. Thenφ(IGn,2)>χ(IGn,2). Besides,IG2k,k ∼=K2andφ(IG2k,k)=2.

Theorem 4φ(IGn,2)≥n −2.

ProofWe give the graphIGn,2a(n−2)-coloringf:V1={{1,3},{1,4},··· ,{1,n−1}};V2={{2,4},{2,5},··· ,{2,n}};···;Vn−2={{n −2,n}}.

Firstly, for anyA,B ∈Vi, we haveA ∩B={i}. ThenViis an independent set ofIGn,2. Besides,{1,n−1},{2,n−1},··· ,{n−3,n−1},{n−2,n}areb-vertices. Hencefis ab-colouring ofIGn,2and thenφ(IGn,2)≥n −2.

Theorem 5φ(IGn,3)≥n −4.

ProofWe give the graphIGn,3a (n −4)-coloringf:

Vn−4={n −4,n −2,n}.

Firstly, for anyA,B ∈Vi, we haveA ∩B={i}. ThenViis an independent set ofIGn,3. Besides,{1,n −3,n −1},{2,n −3,n −1},··· ,{n −5,n −3,n −1},{2,n −2,n}areb-vertices. Hencefis ab-colouring ofIGn,3and thenφ(IGn,3)≥n −4.

Note that the vertexv0={n,n −2,··· ,n −2(k −1)}ofIGn,kis the vertex such that ∑i∈[k]xiis maximized for anyv={x1,x2,··· ,xk} ∈V(IGn,k). Hence, we have the following conjecture.

Conjecture 1φ(IGn,k)≥n −2(k −1).

By the aid of computer programs, we obtain theb-chromatic numbers of the interlacing graphsIGn,2andIGn,3with smalln. Specifically, we first generate the interlacing graphsIGn,2andIGn,3onnvertices; then compute the parameterm(IGn,k)[7]ofIGn,k; finally, we determine whetherIGn,khas ab-coloring oftcolors, wheret=m(IGn,k),m(IGn,k)−1,···. By this process,we compute theb-chromatic numbers of the interlacing graphsIGn,2andIGn,3withn ≤8, as shown in Table 1.

Table 1 The b-chromatic numbers of IGn,2 and IGn,3 with n ≤8

Moveover, we give theb-colorings ofIG5,2,IG6,2andIG7,2in Figure 2 and theb-colorings ofIG7,3andIG8,3in Figure 3.

Figure 2 The b-colorings of IG5,2, IG6,2 and IG7,2

Figure 3 The b-colorings of IG7,3 and IG8,3