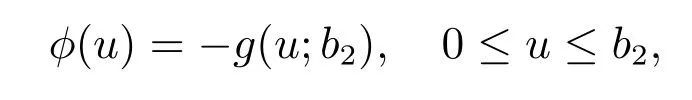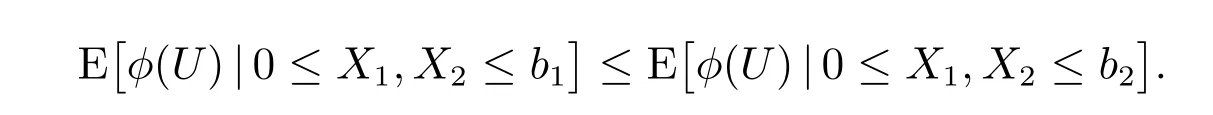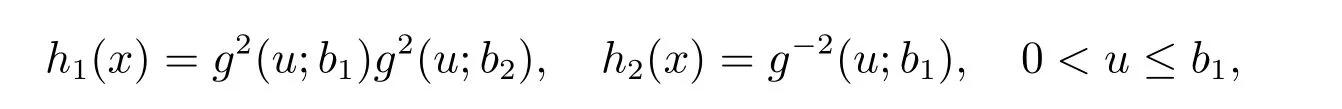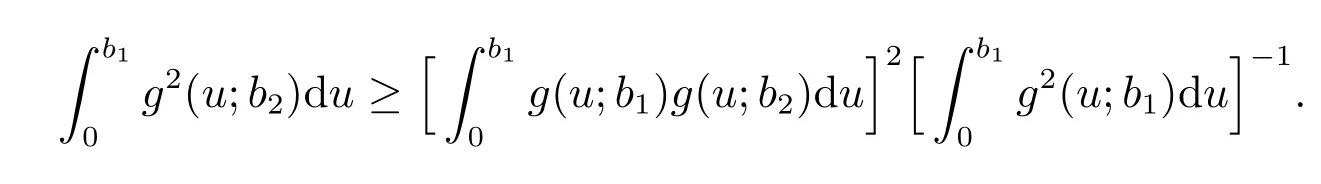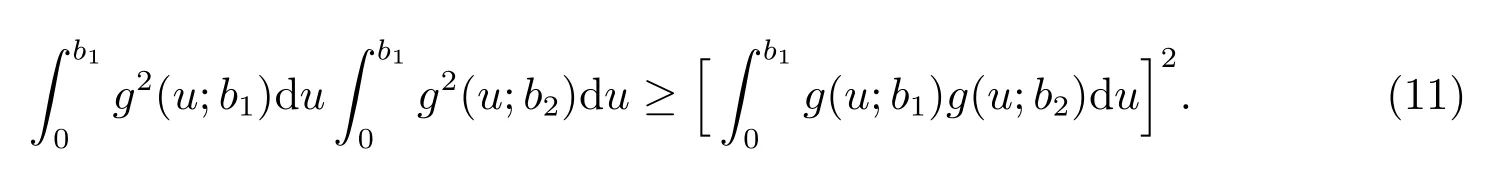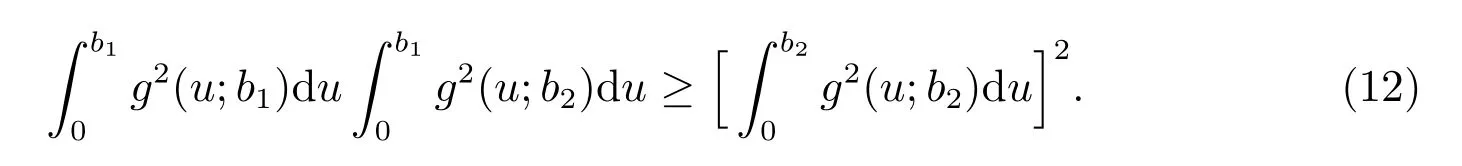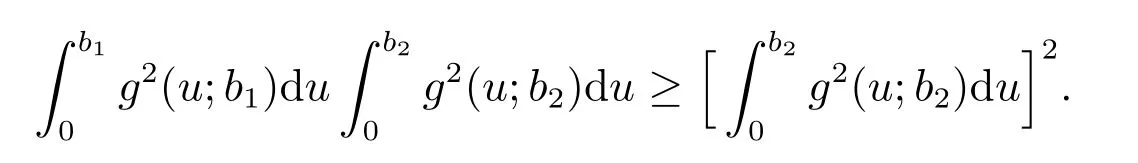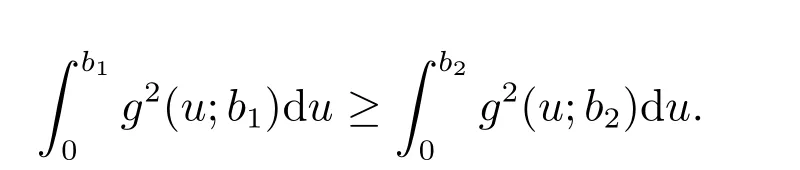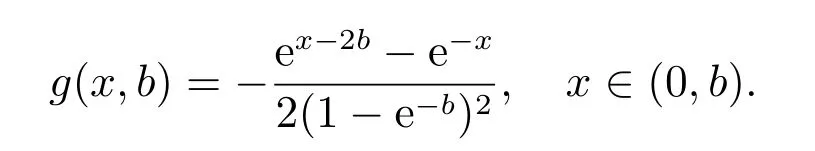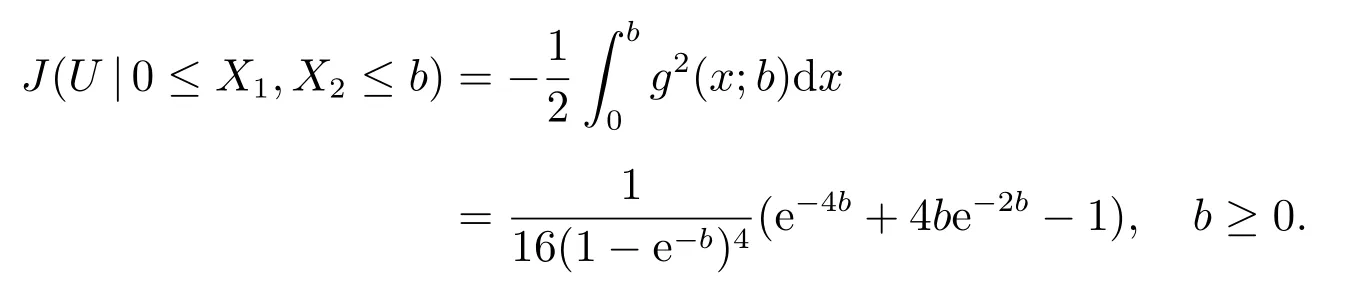Partial Monotonicities of Extropy and Cumulative Residual Entropy Measure of Uncertainty

PU Ming-yue QIU Guo-xin†

(1- School of Accounting and Finance, Xinhua University of Anhui, Hefei 230088;2- School of Management, University of Science and Technology of China, Hefei 230026)

Abstract: Uncertainty is closely related to amount of information and has been extensively studied in a variety of scientific fields including communication theory, probability theory and statistics. Given the information that the outcome of a random variable is in an interval, the uncertainty is expected to reduce when the interval shrinks.However, this conclusion is not always true. In this paper, we present the conditions under which the conditional extropy/cumulative residual entropy is a partially monotonic function of interval. Similar result is obtained for extropy of convolution of two independent and identically distributed random variables if their probability density functions are log-concave.

Keywords: cumulative residual entropy;entropy;extropy;log-concavity;partially monotonicity

1 Introduction

One of the most important measures for uncertainty is Shannon’s differential entropy which was defined by Shannon[1]as follows

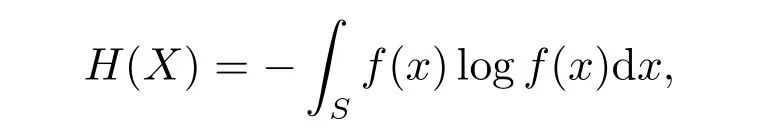
wherefis the probability density function (pdf) of an absolutely continuous random variable (rv)Xwith supportS. Shannon’s differential entropy has many applications in information science, communication, coding, probability, statistics and other related fields, see Makkuva and Wu[2], Kuntalet al[3], Saifet al[4]and references therein.

In the past half century,several generalizations of the Shannon’s differential entropy have been proposed for quantifying uncertainty in the literature. For example, R´enyi[5]and Tsallis[6]both proposed generalized entropies by means of an additional parameterα. R´enyi’s entropy with orderαforXwas defined as

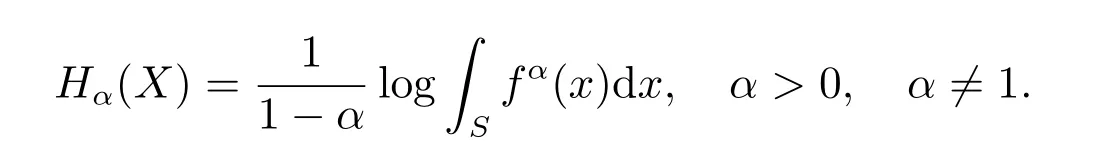
It should be noted thatHα(X)→H(X) asα →1. Tsallis’s entropy with orderαforXwas defined as

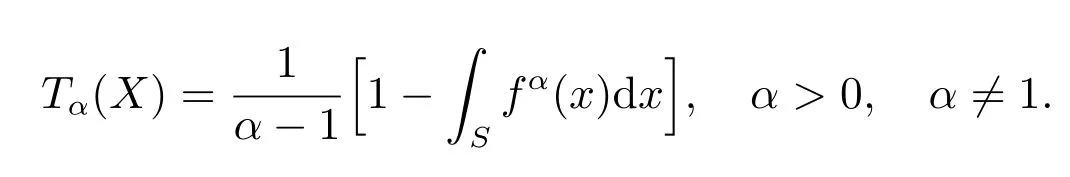
Similarly,Tα(X)→H(X) asα →1. Further, Kapur[7]proposed a more generalized version of R´enyi’s entropy with parameterαand an additional parameterβ. Kapur’s entropy forXcan be written as

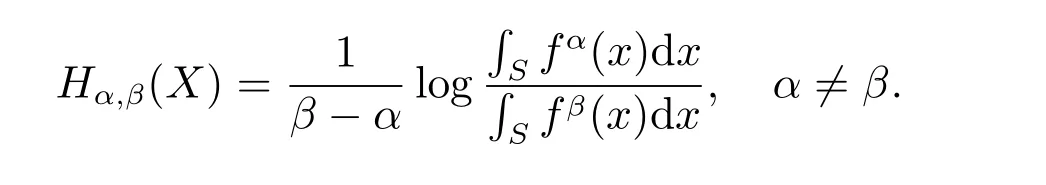
We also note thatHα,β(X)=Hα(X) whenβ=1.

Recently,Raoet al[8]and Ladet al[9]generalized the Shannon’s differential entropy following two different lines. The former noted that the Shannon’s differential entropy is only defined for distributions with densities,and then defined his cumulative residual entropy based on the survival function ofXas follows

where ¯F= 1−FandFare survival function and cumulative distribution function(cdf)ofX, respectively. While the latter found that the Shannon’s differential entropy has a complementary dual function and then termed this complementary dual function as the extropy ofX. The extropy ofXis given by

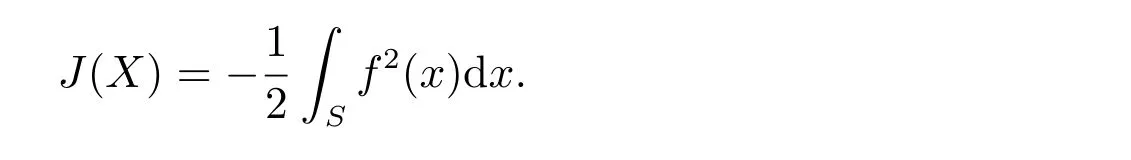
For more on the cumulative residual entropy and the extropy ofX, one may refer to Baratpour[10], Navarroet al[11], Park and Kim[12], Qiu[13], Qiu and Jia[14,15].

LetA={a ≤X ≤b}be an event,then the conditional probability density function ofXgivenAcan be expressed as

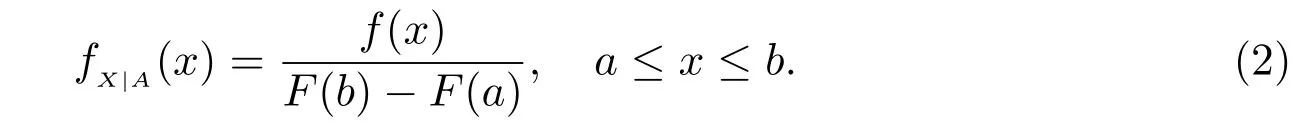
Thus, the conditional Shannon’s differential entropy ofXgivenAis formulated as

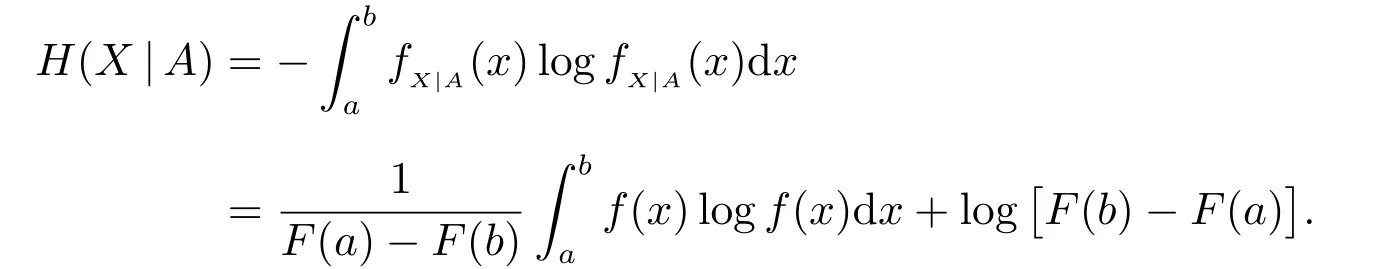
For a review of the conditional Shannon’s differential entropyH(X|A), one may refer to Sunojet al[16].

IfAandBare two intervals such thatH(X|A)≤H(X|B) andA ⊆B, then we say the conditional Shannon’s differential entropyHis partially monotonic. As discussed in Chen[17], Shangari and Chen[18], Gupta and Bajaj[19], it is interesting to investigate the conditions under which the conditional Shannon’s differential entropy and its generalized versions are partially monotonic with respect to their condition sets. This question was firstly considered by Shangari and Chen[18]for the conditional Shannon’s differential entropy and the conditional R´enyi’s entropy. Gupta and Bajaj[19]considered similar question for the conditional Tsallis’s entropy and the conditional Kapur’s entropy. In sections 2 and 3, we will give respectively the conditions under which the conditional extropy and the conditional cumulative residual entropy are partially monotonic with respect to their condition sets.

LetX1andX2be two independent and identically distributed(iid)copies of the rvX. Therefore,some function ofU=X1−X2can be viewed as a measure of uncertainty associated with its reproducibility and precision. Chen[17]proved that ifX1andX2are two iid rv’s with log-concave pdf’s, then the Shannon’s differential entropy ofUgiven thatX1andX2take a value in the intervalB={a ≤X1,X2≤b}is partially monotonic inB. IfX1andX2have log-concave pdf’s, Shangari and Chen[18]claimed that the conditional R´enyi entropy with orderαofUgivenB={a ≤X1,X2≤b}is a partially increasing function ofBifα> 1, and a partially decreasing function ofBif 0<α< 1. Gupta and Bajaj[19]proved that the conditional Tsallis’s entropy and the conditional R´enyi entropy ofUgivenB={0≤X1,X2≤b}are partially increasing functions ofBfor allα> 0, α ̸= 1 ifX1andX2have log-concave pdf’s. In section 4, we will show that the conditional extropy ofUgivenB={0≤X1,X2≤b}is also partially monotonic inBifX1andX2have log-concave pdf’s.

Throughout this paper,all rv’s are implicitly assumed to be absolutely continuous.The term increasing(decreasing)is used for monotone non-decreasing(non-increasing).

2 Partial monotonicity of extropy

According to (2), the conditional extropy ofXgivenA={a ≤X ≤b}can be expressed as

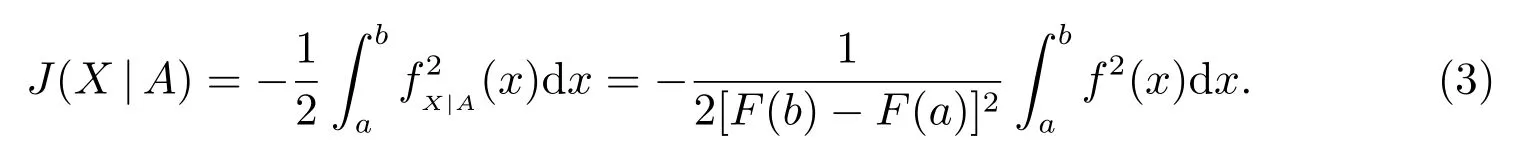
In the following theorem,we provide the conditions under which the conditional extropyJ(X|A) is a partially increasing function of interval [a,b].

Theorem 1LetXbe an rv with pdffand twice-differentiable cdfF. Further,letAbe the event{a ≤X ≤b}. Then:

(a) The conditional extropyJ(X|A) is partially increasing inbifF(x) is logconcave;

(b) The conditional extropyJ(X|A) is a partially increasing function of interval[a,b] iff(x) is log-concave.

Proof(a) We have from (3) that

If we let

then

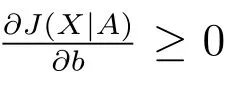
(b) Firstly, we note that the cdf of−Xis given byF−X(x)= ¯F(−x) and

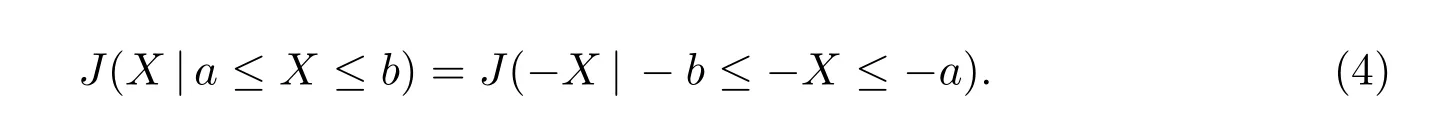
Thus, if ¯F(x) is log-concave,F−X(x) is also log-concave. By Theorem 1(a), we haveJ(−X|−b ≤−X ≤−a) is partially increasing in−a. Hence,H(X|a ≤X ≤b) is partially decreasing inaby (4).

Finally, we recall that the log-concavity off(x) implies the log-concavity ofFand ¯F. Therefore, iff(x) is log-concave, it follows from Theorem 1(a) and the above discussion thatJ(X|A) is a partially increasing function of interval [a,b].

Using symmetry, Shangari and Chen[18]proved the following Proposition 1.

Proposition 1LetXbe an rv with pdffand twice-differentiable cdfF. Further,letAbe the event{a ≤X ≤b}. Then the conditional Shannon’s differential entropyH(X|A) is a partially increasing function of interval [a,b] ifF(x) is log-concave.

Unfortunately, Proposition 1 and its proof provided by Shangari and Chen[18]are wrong. Under the assumptions of Proposition 1, we can only say that the conditional Shannon’s differential entropy is partially increasing inb. But, we can’t guarantee from symmetry that it is partially decreasing ina. Xia[20]first noted this blemish,and provided an counterexample to illustrate it. Moreover, Xia[20]gave a sufficient condition under whichH(X|A) is a partially increasing function ofA= [a,b]. Next,we present another counterexample and give an alternative sufficient condition for the partially monotonicity ofH(X|A).

Counterexample 1 LetXbe a Cauchy distributed rv with cdfF(x) =π/2+arctan(x), x ≥0. Obviously,F(x) is log-concave in [0,∞). However, if we letAbe the event{0≤a ≤X ≤10}, then

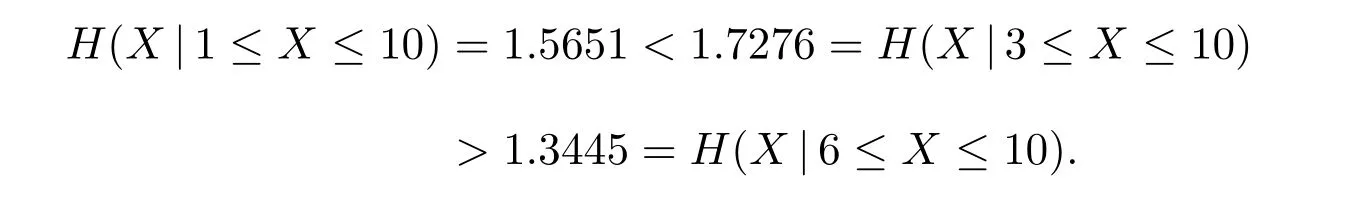
This implies that the conditional Shannon’s differential entropyH(X|a ≤X ≤10) is not partially decreasing ina ≥0.

Theorem 2LetXbe an rv with pdffand twice-differentiable cdfF. Further,letAbe the event{a ≤X ≤b}. Then the conditional Shannon’s differential entropyH(X|A) is a partially increasing function of interval [a,b] iff(x) is log-concave.

ProofIff(x)is log-concave,thenFis log-concave. Thus,H(X|A)is a partially increasing function ofbby Lemma 2.2 in Shangari and Chen[18]. Moreover, iff(x) is log-concave,then ¯Fis also log-concave. Using similar manners in the proof of Theorem 1(b), we haveH(X|A) is a partially decreasing function ofa. Therefore, the derived result is proved.

3 Partial monotonicity of cumulative residual entropy

The survival function ofXgivenA={a ≤X ≤b}is given by

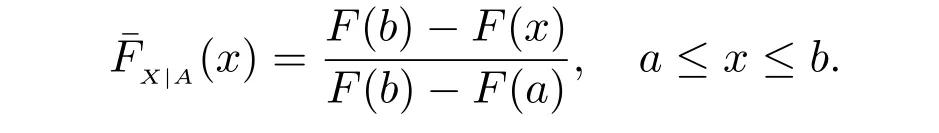
According to (1), the conditional cumulative residual entropyCRE(X|A) is given by

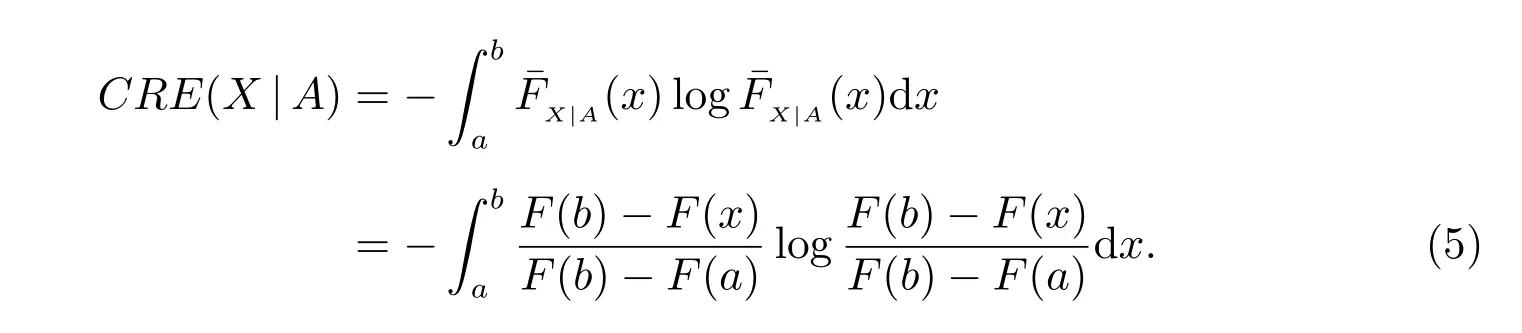
Suppose thatF(b)=1. Then, (5) can be reduced to

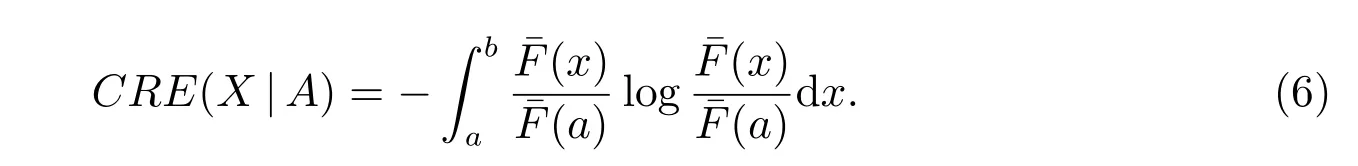
Next, we will show the conditions under whichCRE(X|A) in (6) is decreasing ina.

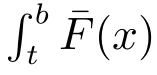
ProofNote that (6) can be rewritten as

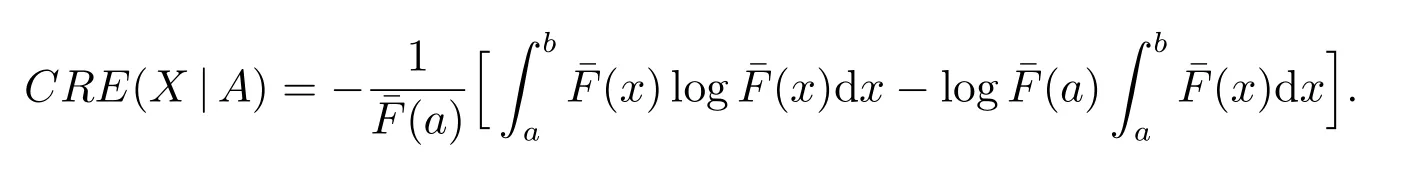
Thus

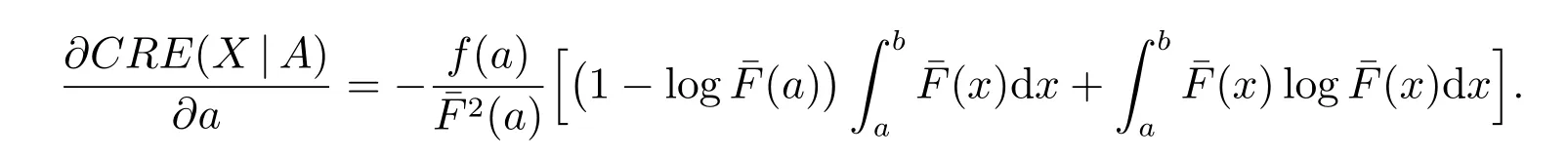
Letting

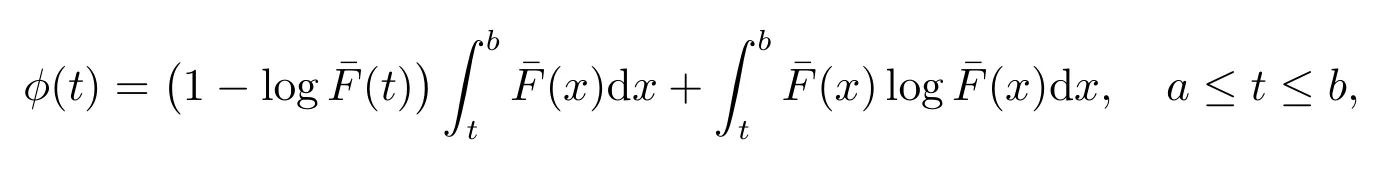
we have

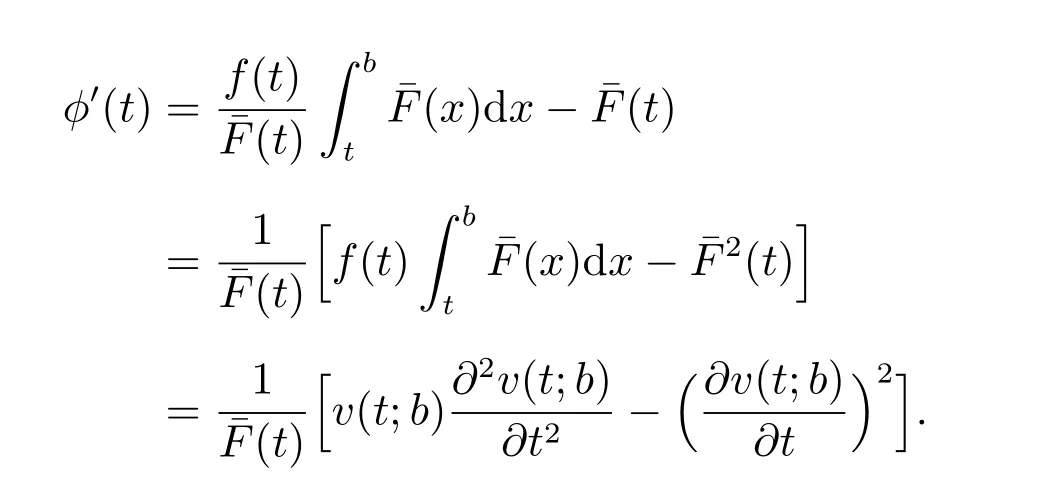
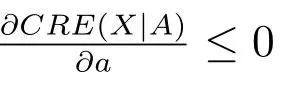
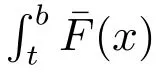
The conditionF(b)=1 in Lemma 1 is used only for ease of presentation. Removing this condition, we now state the general result in the following theorem.

Theorem 3LetXbe an rv with pdffand twice-differentiable cdfF. Further,letAbe the event{a ≤X ≤b}. ThenCRE(X|A)given in(5)is a partially decreasing function ofaifF(x) is log-concave.

ProofLetXbbe an rv with survival function

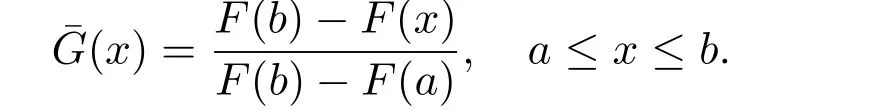
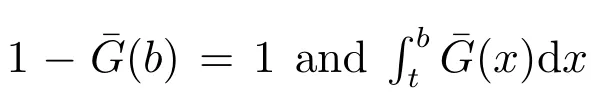
Thus,CRE(X|A) given in (5) is a partially decreasing function ofa.

4 Partial monotonicity of convolution

LetX1andX2be two iid copies ofXandU=X1−X2. The conditional R´enyi entropy of orderαforUgivenB={0≤X1,X2≤b}can be expressed as

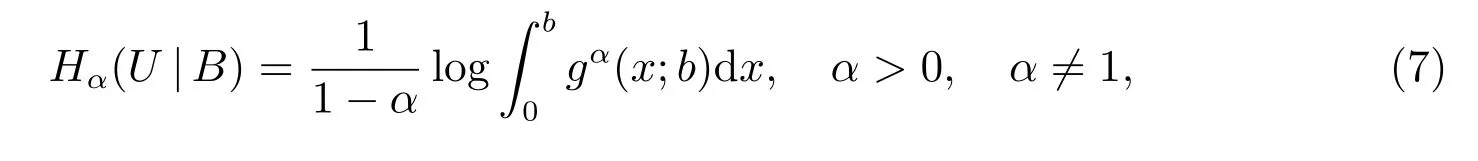
where

is the pdf ofUgivenB={0≤X1,X2≤b}. As mentioned in the end of section 1,Theorem 3 in Gupta and Bajaj[19]proved that ifX1andX2have log-concave pdf’s,then the conditional R´enyi entropy of orderαforUgivenB={0≤X1,X2≤b}is a partially increasing function ofbfor allα> 0, α ̸= 1. Puttingα= 2 in (7), we have the result that∫b0g2(x;b)dxis partially decreasing inbifX1andX2have log-concave pdf’s. Further, we have the result that

is partially increasing inbifX1andX2have log-concave pdf’s, whereJ(U|B) is the conditional extropy ofUgivenB={0≤X1,X2≤b}. That is, we have the following Theorem 4.

Theorem 4IfX1andX2have log-concave pdf’s, then the conditional extropy ofUgivenB={0≤X1,X2≤b}is a partially increasing function ofB.

Next, we give an alternative proof of Theorem 4 based on the following three lemmas.

Lemma 2[17]IfX1andX2have log-concave pdf’s, then the pdfg(x;b) ofU=X1−X2givenB={0≤X1,X2≤b}is decreasing inx ∈(0,b).

Lemma 3[17]LetX1andX2have log-concave pdf’s. If the functionϕ(u) is increasing inu,then E[ϕ(U)|0≤X1,X2≤b]is increasing inb ≥0,whereU=X1−X2.

Lemma 4[21]Let

For any two functionsh1(x)≥0, h2(x)≥0, H¨older inequality for integrals states that

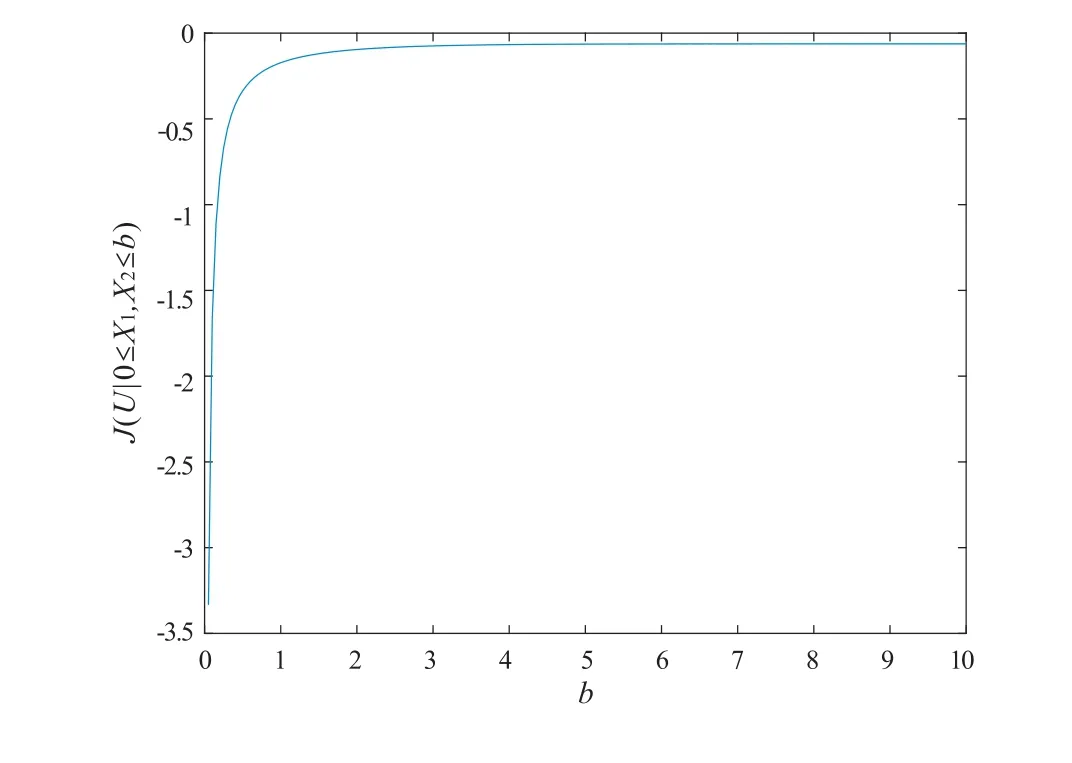
Proof of Theorem 4The conditional extropy ofUgivenB={0≤X1,X2≤b}can be expressed as

For fixed 0

thenϕ(u) is increasing inuby Lemma 2. For allb1≤b2, it follows from Lemma 3 that

That is

On the other hand, if we let

andp=1/2, q=−1, then by Lemma 4, we have

This implies

Combining (10) and (11), we further have

Note that

sinceb2≥b1. It follows from (12) that

Or, equivalently,

Therefore, it holds that

This completes the proof of Theorem 4.

To end this section, we give an example to illustrate the conclusion of Theorem 4.

Example 1LetX1andX2be exponentially distributed rv’s with pdff(x) =e−x, x ≥0, which is log-concave. Using (8), we have

This implies

Figure 1 plots the functionJ(U|0≤X1,X2≤b) whenbchanges from 0 to 10. It is easy to see from Figure 1 thatJ(U|0≤X1,X2≤b) is increasing inb, which verifies Theorem 4.

Figure 1 Plot of the function J(U|0 ≤X1,X2 ≤b) when b changes from 0 to 10