纸条平结与正五边形

姜伯驹

(北京大学数学科学学院 100871)

1 纸条平结

西北工业大学杨智春教授发问：“我发现，一根长矩形纸条打个平结，得到一正五边形,这个有证明吗？ ”

2 构图

纸条平结产生五边形ABCDE的构图如下图.纸条的一侧是折线BCABE，另一侧是折线ADECD.图中的浅细线都是(从顶点到边延长线的)垂线， 并且画出了相应的辅助直角三形，浅细线长度都等于纸条的宽度。 我们将证明五边形ABCDE是正五边形.

3 正五边形

以AB和BC为斜边并在B处有对顶锐角的那两个辅助直角三角形，对边也相等(浅细边)，所以全等.于是AB=BC.同理可知BC=CD与CD=DE.五边形的另一条边AE尚未知，因为它不在纸条的边缘上.

以AE为斜边那两个辅助直角三角形，斜边相同，浅细边相等，所以全等，于是五边形在A处与E处的外角相等，因而内角 ∠A=∠E.同理可知∠B=∠C与∠C=∠D.∠A与∠B是否相等尚未知，也是因为AE不在纸条的边缘上.

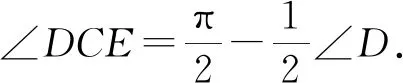
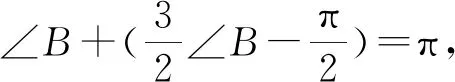
再比较以AB和AE为斜边的两个辅助直角三形，有一对锐角相等(分别是A处与B处的外角)， 对边也相等(浅细边)，所以全等. 因而AB=AE.五条边也全部相等了.

由此可见， 五边形ABCDE是正五边形！