基于拉格朗日插值的电子耳蜗分数延迟和参数失配分析

张春晓，陈又圣，黄鸿展

深圳信息职业技术学院，广东深圳518000

前言

目前电子耳蜗在干扰噪声环境下的识别率仍然不高，提高前端信号采集的信噪比是提高言语识别率的重要途径之一。在电子耳蜗实际使用中，目标信号与干扰噪声往往方位不一致，例如面对面交流和打电话交流过程中的干扰噪声主要来自其他方位，来自正向方位的语音信号是常见使用场景中的目标信号［1］。麦克风阵列波束形成的方法由于增加了空间方位的信息，在近年来被应用于电子耳蜗前端语音增强中［2-5］。在基于麦克风阵列的语音增强方法中，延迟波束形成技术由于实现简单和计算量少等特点被目前电子耳蜗领域的前端信号采集和语音增强算法研究所采用［6-9］。

延迟波束形成方法中的延迟系数是决定波束指向类型的重要参数［10-11］，但在电子耳蜗小尺寸间距及语音采样率条件下，延迟具体数值往往不是整数，由此产生了分数延迟参数的实现及信号插值的问题［12］。就本质而言，分数延迟是在已有的信号采集点之间插值形成新的信号序列作为估计的延迟信号，并进一步用于语音增强算法中。

插值可以大体分为有限长单位冲激响应滤波器（Finite Impulse Response,FIR）和无限脉冲响应数字滤波器（Infinite Impulse Response,IIR）方法两大类，其中，拉格朗日插值方法由于其算法简单，易于率先实现等特点在很多领域应用较广［13-16］。由于尺寸限制及功耗要求，电子耳蜗对信号处理的实时性有较高要求，本文使用拉格朗日插值方法来实现电子耳蜗波束形成中的分数延迟，并探讨该插值方法的参数特征和失配特性。

1 电子耳蜗波束形成及分数延迟

1.1 延迟参数及波束指向

对电子耳蜗实际应用来说，双麦克风的模式由于算法简单，计算复杂度低而被应用于前端信号采集及语音增强中。延迟参数是决定波束指向的重要参数，而延迟参数一般以d/c 的倍数形式来表示，其中，d表示双麦克风的间距，c表示声速。双麦克风等权重情形下，不同延迟参数条件下不同方位的信号幅频响应如图1所示。

图1 不同延迟条件下系统各个方位的幅频响应Fig.1 System amplitude response for different delay conditions at different orientations

图1 表示不同延迟参数条件下系统各个方位的系统幅频响应曲线，其中，0°方位表示正向，-90°和90°方位表示侧向，-180°和180°方位表示后向（-180°和180°位置重合）。从图1 可以看到，不同的延迟参数会产生不同的系统幅频响应曲线，由此产生了不同的波束指向。例如，延迟参数为0 时，正向和后向方位的幅频响应相同，而侧向幅频响应为0，对应双极型波束指向；延迟参数为d/c时，正向的幅频响应最大，而后向的幅频响应为0，对应心型波束指向。因此，延迟参数决定着极性图的类型，在波束指向设计中，延迟参数对精度有很高的要求。

1.2 分数延迟

在电子耳蜗实际应用中，由于体积的限制，电子耳蜗本身所使用的双麦克风间距较小。例如，延迟一个d/c在采样率为22.05和44.10 kHz条件下分别对应延迟0.649 和1.297 个采样点，由此产生了分数延迟的问题。延迟0.649 和1.297 个采样点实质上是在原来采集信号的基础上实现插值，对于第i个采样点x(i)，延迟0.649是在采样点x(i)和采样点x(i+1)之间插值，而延迟1.297 是在采样点x(i+1)和采样点x(i+2)之间插值。

2 拉格朗日插值

2.1 拉格朗日插值表达式

拉格朗日插值是一种多项式的插值方法，其特点是实现简单。对于原始采集的信号序列x(1)、x(2)、x(3)、…、x(n)，拉格朗日插值多项式L(x)如式（1）所示：

其中，Gj(x)为加权系数函数，其表达式如式（2）所示：

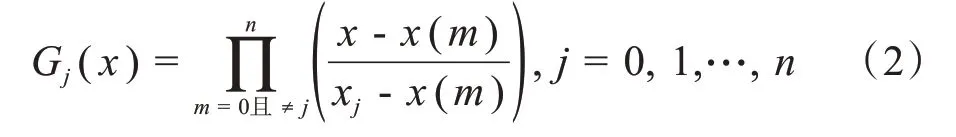
对于分数延迟D个采样点，则采样序列由x(1)、x(2)、…、x(n)变成延迟信号序列L(1+D)、L(2+D)、L(3+D)、…、L(n+D)。对于前面所探讨的电子耳蜗实际尺寸参数来说，延迟一个d/c在22.05 kHz的采样率条件下形成新的序列：L(1.649)、L(2.649)、L(3.649)、…、L(n+0.649)；同样地，在44.1 kHz 采样率条件下形成新的序列：L(2.297)、L(3.297)、L(4.297)、…、L(n+1.297)。

2.2 分数延迟及分数采样点数值计算

对于不同的阶数，拉格朗日插值可形成特定的插值模式。一阶的拉格朗日插值形成最简单的线性插值方法，如果用原始采集的信号序列x(1)、x(2)、x(3)、…、x(n)来表示延迟序列，则对于延迟0.649和1.297个采样点所形成的信号序列如式（3）和（4）所示：

从式（3）和（4）可以看到，一阶的拉格朗日插值是对相邻两点的插值，并通过给予相邻两点的加权形成新的信号延迟的插值点。同样地，N阶的拉格朗日插值是通过相邻的N个点的加权形成的。

3 拉格朗日插值的特征及失配分析

3.1 插值滤波器的幅频响应失配

从式（3）和（4）可以看到，一阶的拉格朗日插值是对相邻两点的插值，并通过给予相邻两点的加权形成新的信号延迟的插值点。同样地，N阶的拉格朗日插值是通过相邻的N个点加权和形成的。而从系统输入输出角度看，通过拉格朗日插值方法实现的插值可以看成是一个延迟滤波器。

如果延迟D个采样点，则理想的分数延迟滤波器的系统函数Hideal表达式如（5）所示：

由式（5）可以看到，理想的分数延迟滤波器是具有线性相位的全通系统，即系统幅频响应恒为1，相位具有线性变化的特征。由于线性相位的全通系统是非因果系统，不能实时实现，因此不适合直接应用在电子耳蜗实时信号处理的过程中。对于实时处理的拉格朗日插值方式，其对应的滤波器系统响应存在失配，在采样率22.05 和44.1 kHz 条件下延迟一个d/c的拉格朗日插值滤波器在不同阶数情形下的系统幅频响应分布如图2所示。

图2 表示阶数为1～10 时拉格朗日插值滤波器系统幅频响应分布情况。对比不同阶数和归一化频率条件下的幅频响应变化，可以看到，当频率较小时，系统的幅频响应变化不大。归一化频率范围在0～0.1fs（采样率22.05 kHz 时对应的频带范围是0～2 205 Hz，采样率44.1 kHz 时对应的频带范围是0～4 410 Hz）时的幅频响应几乎为1，与理论的分数延迟滤波器的幅频响应一致性较好。而当频率增大时，幅频响应的变化增大，有正的偏差和负的偏差，并且阶数越大，高频位置的幅频响应偏差越大。因此，拉格朗日插值滤波器在低频位置的误差较小，高频位置误差较大，高阶会增大高频误差。

图2 不同阶数的拉格朗日插值滤波器系统幅频响应分布Fig.2 System amplitude response distribution of Lagrange interpolation filter for different filter orders

3.2 插值滤波器的相频响应失配

在采样率是22.05 kHz和44.1 kHz条件下延迟一个d/c的拉格朗日插值滤波器在不同阶数情形下的系统相频响应曲线如图3所示。

图3对比了不同阶数的拉格朗日插值滤波器系统相频响应曲线，其中图3a和图3c分别是直接通过反正切计算拉格朗日插值滤波器在采样率是22.05 kHz和44.1 kHz条件下延迟一个d/c的相位曲线结果。从图3a和图3c可以看到，部分阶数条件下高频位置会出现曲线的跳变，这是由于计算时反正切的相位范围是-π～π，因此超过该范围会出现跳变。进一步通过解卷绕得到对应的实际相位曲线图3b 和图3d。在图3中，理想分数延迟滤波器的相位是线性变化的（黑色虚线），而拉格朗日插值滤波器的相位则是非线性的曲线。当归一化频率较小时（0～0.2fs频段），相位线性度好，与理想分数延迟滤波器的相位非常接近，当归一化频率大于0.2fs时，相位失配增大。从高频的相位曲线分布看，拉格朗日插值滤波器相位与理想分数延迟滤波器的相位的失配包括正的偏差和负的偏差，阶数增大时失配更大。

4 结论

本文采用拉格朗日插值的方式实现电子耳蜗延迟参数的实现，分析了拉格朗日插值的特征和分数延迟的参数，并从多参数情形下研究了拉格朗日插值对分数延迟失配的影响。拉格朗日插值多项式从表达式看是多项式的插值方法，其功能是通过相邻的若干个点的值加权求和形成的预测值。拉格朗日插值具有低频位置幅频响应和相频响应误差最小化的特征，有助于应用于电子耳蜗的分数延迟实现。

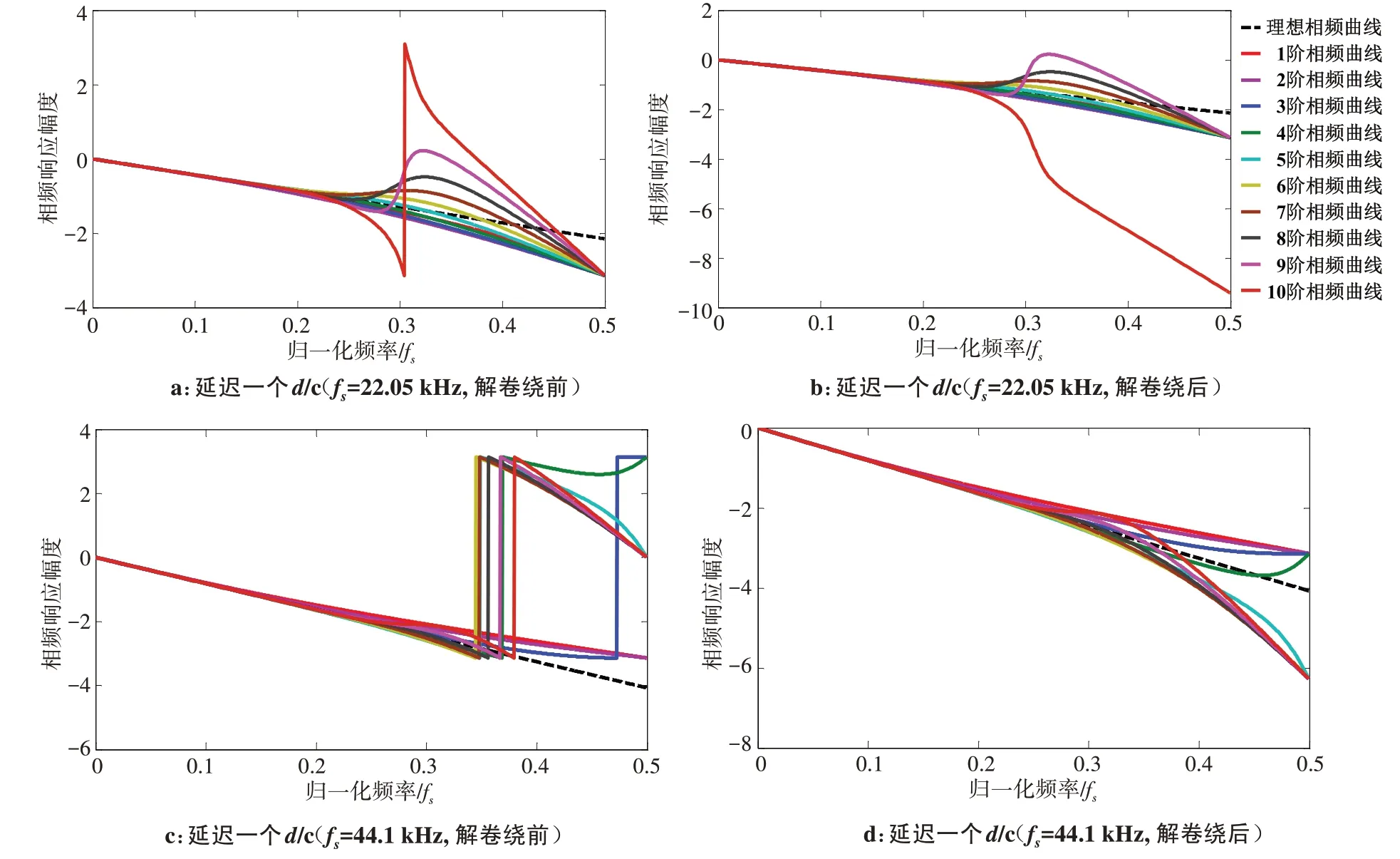
图3 不同阶数的拉格朗日插值滤波器系统相频响应曲线Fig.3 System phase response curves of Lagrange interpolation filter for different filter orders