多级行星轮系结构与运动拓扑模型的图形符号描述方法及其运动学分析
王均刚, 杨士男, 刘燕德, 曾礼平, 墨蕊娜
(1.华东交通大学 机电与车辆工程学院,江西 南昌 330013; 2.华东交通大学 理学院, 江西 南昌 330013)
行星齿轮传动因其特殊的结构和优良的传动性而被广泛应用于各种机械传动系统。与单级行星轮系相比,多级行星轮系的结构复杂,包含的构件更多,对多级行星轮系的分析设计十分困难[1-2]。
国内外学者日益重视应用图形符号对行星轮系进行结构拓扑分析,提出了丰富的图论表示方法[3-6]。薛隆泉等[7]基于功能离散法提出行星轮系的拓扑图转化理论,通过拓扑变换过程、借用不同的符号表示出行星轮系中各构件以及构件间不同的联接特征,最终形成以点、线组成的图形,但其在整体结构拓扑性表达方面存在欠缺。雷亚荣[8]在文献[7]基础上,完善了拓扑图的转化理论,确立行星轮系系统化研究的图形模型,见图1,但是其对构件的符号表示以及构件间的联接性质仍未作到明确的区分,整体结构情况不完整,缺少机架与其他构件的联接关系,各构件间的联接特征不明确,齿轮内啮合和外啮合无法进行区分。
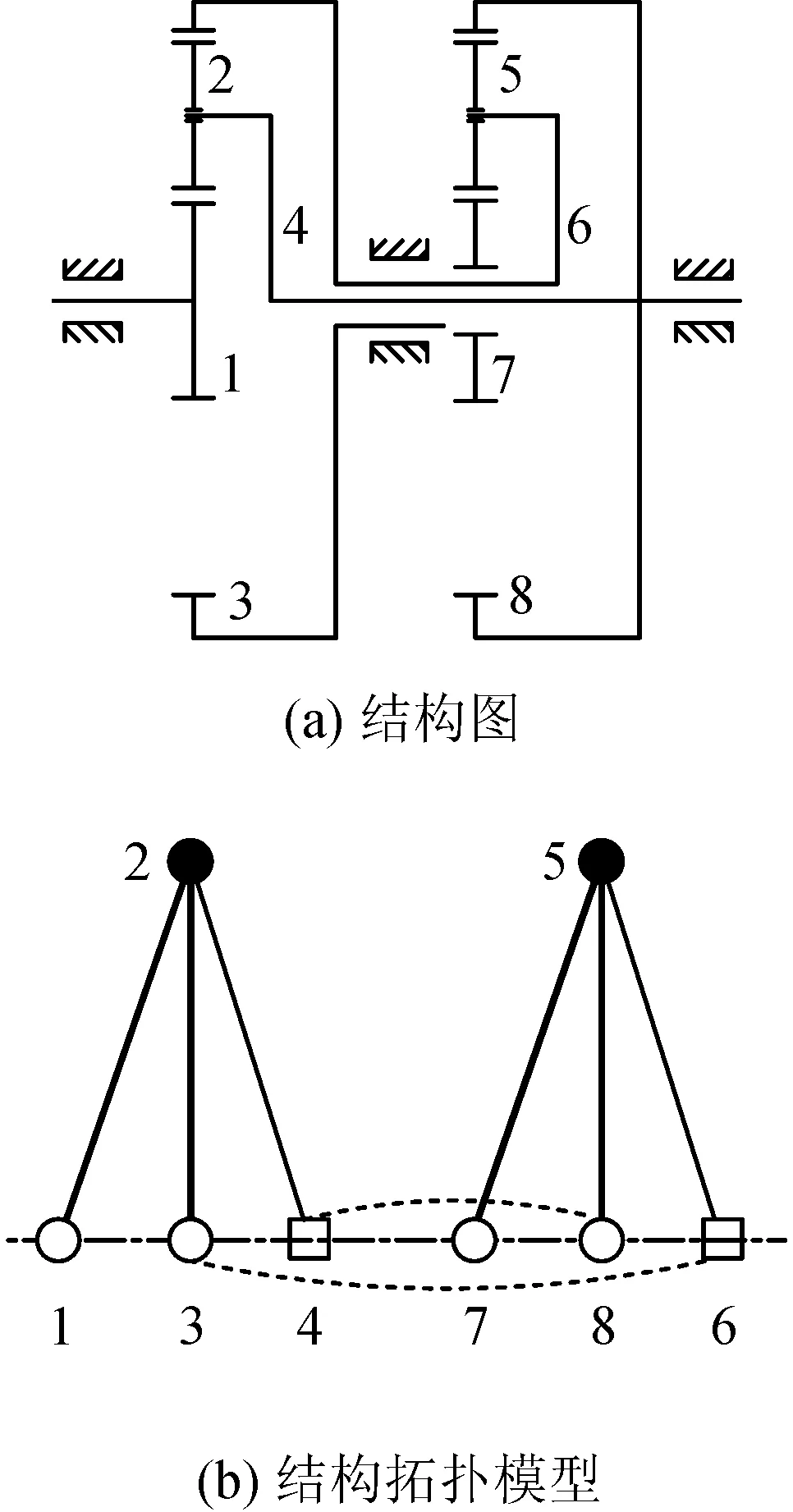
图1 两级行星轮系结构图及结构拓扑模型[8]
文献[9-12]基于图论理论,对行星齿轮传动机构进行构型方案设计。Ding等[13]提出了新双色拓扑图和三色拓扑图的方法,并在平面连杆机构的构型综合中取得了很好的效果。李斌等[14]引入新三色拓扑图对行星齿轮机构进行结构描述,见图2,运用新三色拓扑图对行星轮系进行拓扑描述时,虽然能够明确地体现出各构件间的联接特征以及构件的性质,但轮系的整体结构特性反映不太明确。
为了使运算复杂、难以掌握的行星轮系运动学分析变得更为简单和直观, 一些研究者采用图形化方法对行星轮系的运动学进了分析。Tsai等[15]运用方块图法对行星轮系的运动特性进行了分析。GomAyats等[16]针对行星轮系中各构件之间的运动关系以及整个传动系统的传动比分配,提出了一种超图法。Salgado等[17]基于图形表示法对具有多构件的行星轮系功率流与传动效率进行了分析。Gao等[18]在行星轮系中引入速度拓扑图的概念,研究了传动比和拓扑之间的关系。符升平等[19]基于图论理论,提出了一种更适用于计算机建模和求解的行星轮系传动性能分析方法。
由文献可知,采用图形符号能够简化行星轮系的结构设计和运动学分析。但是,用于研究行星轮系结构特征以及运动特性的各类图形化表示呈现发散式研究,各有千秋。尽管有学者研究了统一拓扑描述模型的平面机构的表示方法[20],但目前公开发表的文献尚无针对多级行星轮系的结构特征及运动特征信息运用完善的图形符号进行表示,并且对多级的行星轮系进行结构和运动拓扑描述时相对困难,甚至无法作出其拓扑图。
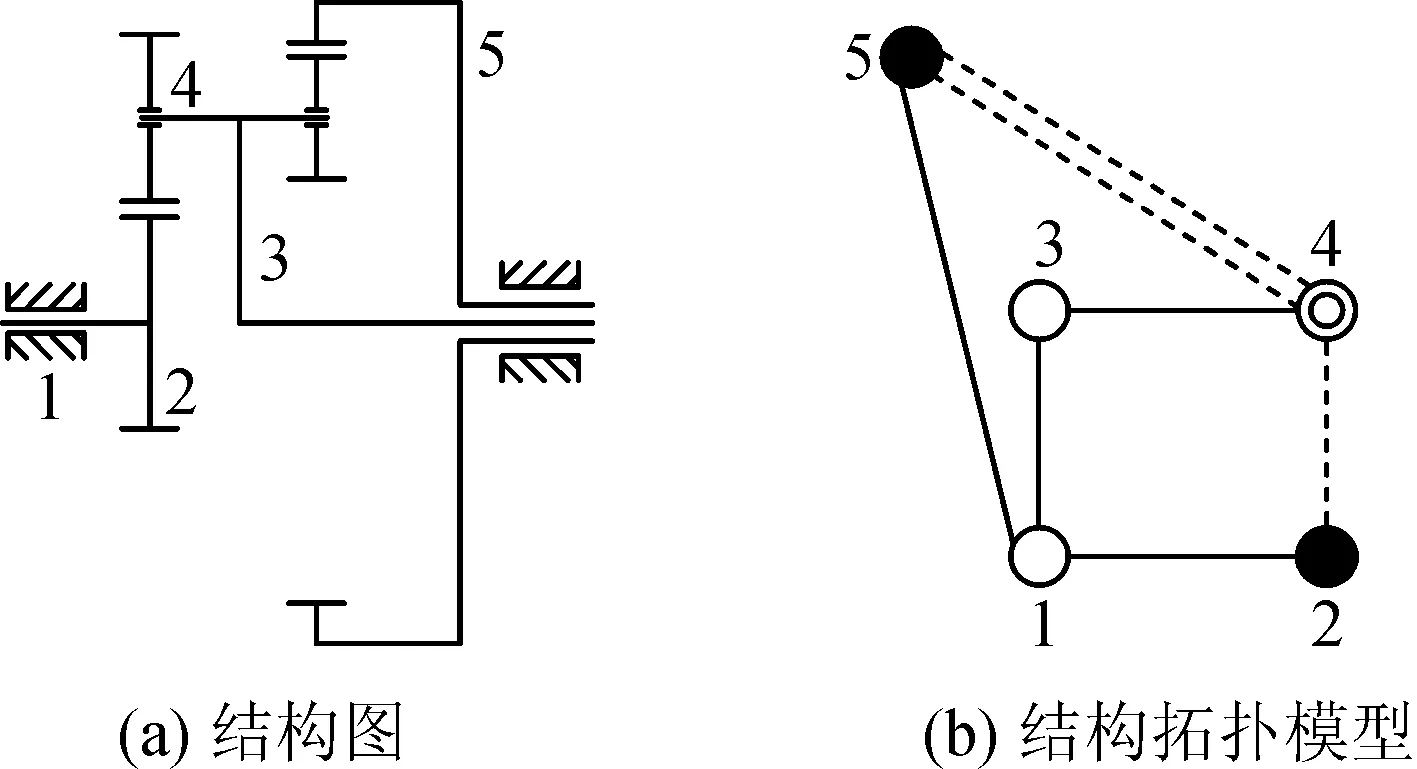
图2 单级行星轮系结构图及结构拓扑模型[14]
本文在已有的研究基础上,提出了对多级行星轮系的结构特征及运动特征信息运用完善的图形符号进行表示方法,该方法能够对多级的行星轮系进行结构和运动拓扑模型进行描述。通过对行星轮系中各构件以及各构件之间的联接关系进行相关的图形符号定义,规定了演化规则及转换方式,提出了能够完整描述行星轮系整体结构特征、运动特性和构件性质明确的统一图形符号表达方法,为行星轮系在实际分析设计过程中提供一种新的方式。其具体分析过程见图3。
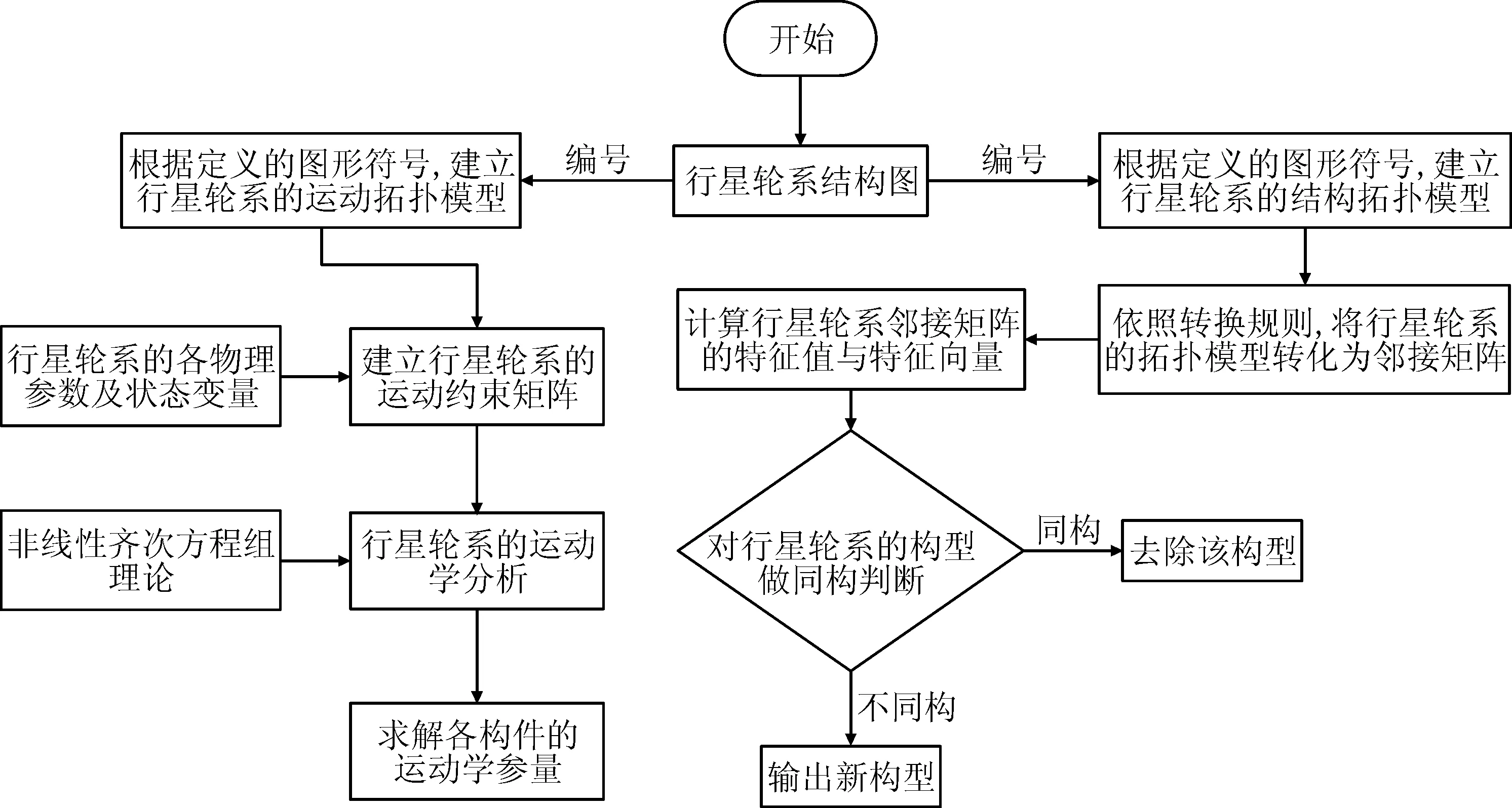
图3 行星轮系拓扑模型建立分析流程图
1 描述行星轮系统新图形符号及其转换规则
应用图论理论对行星轮系进行研究,需要满足以下两种情况:1)拓扑模型反映的行星轮系的整体结构情况是否完整;2)拓扑模型反映的行星轮系的运动性质情况是否明确。同时,这两种情况是根据以下三方面的指标进行分析:①图形的运动拓扑反映是否明确,运动拓扑性具体指轮系各构件间的联接特征;②图形中构件性质是否明确,构件性质具体指轮系中构件的区分度和所属功能;③图形的整体结构拓扑特性反映是否明确,整体结构拓扑特性具体指不同性质的构件所属的层不同。
一般而言,行星轮系是由太阳轮、行星轮、内齿圈、行星架以及机架所组成的传动系统。基于拓扑图转化理论,将行星轮系中各构件转化为不同的图形符号进行描述。
1) 各功能构件符号描述:实心点●表示单行星轮、复合实心点⦿表示双联行星轮;空心点○表示太阳轮;空心方框□表示行星架;实心方框■表示内齿圈;空心三角形△表示机架。
2) 各功能构件的联接关系转化规则:细实线表示回转副;单啮合线表示齿轮外啮合联接;双啮合线表示齿轮内啮合联接,忽略机架与基本构件之间的固结。
3) 根据行星轮系的基本回路特性,在图画的表示中,图形符号表示的基本回路为应满足基本回路数目等于系统的齿轮副数目,且由表示三个基本构件的图形符号、表示齿轮副图形符号、两个回转副图形符号构成的封闭回路。
2 基于新图形符号的多级行星轮系统结构与运动拓扑模型
2.1 多级行星轮系统结构拓扑模型
根据上述中各构件的图形符号定义,现建立图4中两级行星轮系的结构拓扑模型。
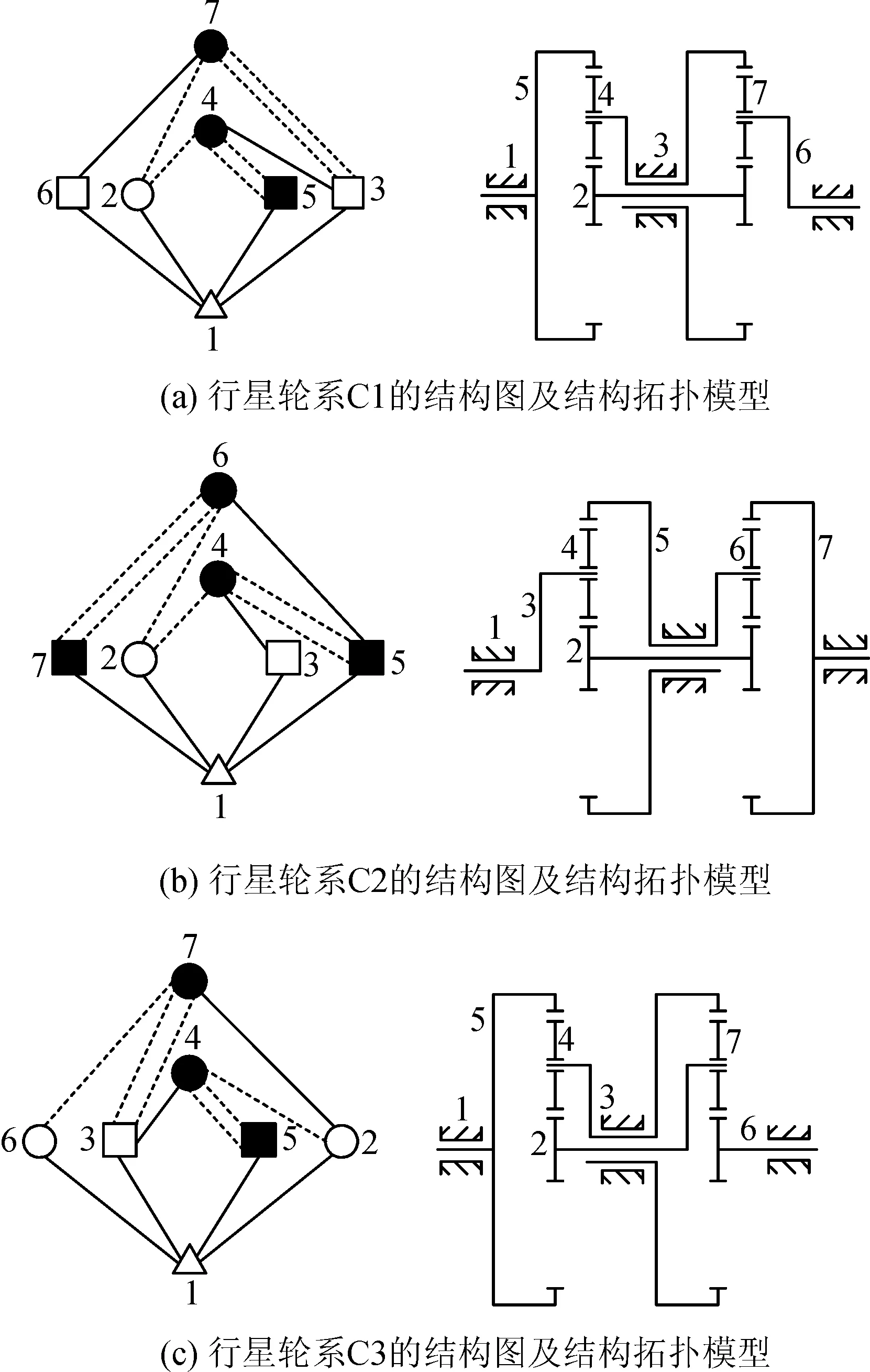
图4 两级行星轮系结构图及结构拓扑模型
将行星轮系的结构图转化为结构拓扑模型表示,其主要优点之一是便于建立行星轮系的邻接矩阵[12],对行星齿轮机构进行同构性判断。行星轮系的邻接矩阵形式以及转换规则为:
(1)
式中:n为机构的构件数,矩阵元素aij(i、j=0,1,2,…,n)。若构件i、j以回转副联接,则aij=1;若构件i、j以外啮合齿轮副联接,则aij=2;若构件i、j以内啮合齿轮副联接,则aij=3;若构件i、j以外啮合齿轮副联接且含有双联行星轮时,则aij=4;若构件i、j以内啮合齿轮副联接且含有双联行星轮时,则aij=5;其余,aij=0。
根据式(1),建立图4中两级行星轮系C1、C2和C3的邻接矩阵A,即:
(2)
(3)
(4)
通过编程,分别计算出邻接矩阵A的特征值及特征向量,具体计算结果见表1~3(其中,第一列为特征值λ,其右方为与该特征值相对应的特征向量φ,φ=[φi]T,i=1,...,7)。通过对比邻接矩阵的特征值和特征向量进行行星齿轮机构之间的同构判断[21]。
通过对比行星轮系C1、C2和C3的邻接矩阵的特征值与特征向量,可知C1与C2的邻接矩阵的特征值完全相同,并且同一特征值所对应的特征向量其各元素对应相等或比例,例如λ3=-0.699 7所对应的特征向量:φ1↔(-φ1)、φ2↔(-φ2)、φ3↔(-φ5)、φ4↔(-φ4)、φ5↔(-φ7)、φ6↔(-φ3)、φ7↔(-φ6),因此,可以判断行星轮系C1与C2为同构运动链;行星轮系C3与C1或C2,首先其邻接矩阵的特征值就不相等,不满足判断条件,因此,行星轮系C3与C1或C2之间的为非同构运动链。

表1 邻接矩阵AC1的特征值和特征向量
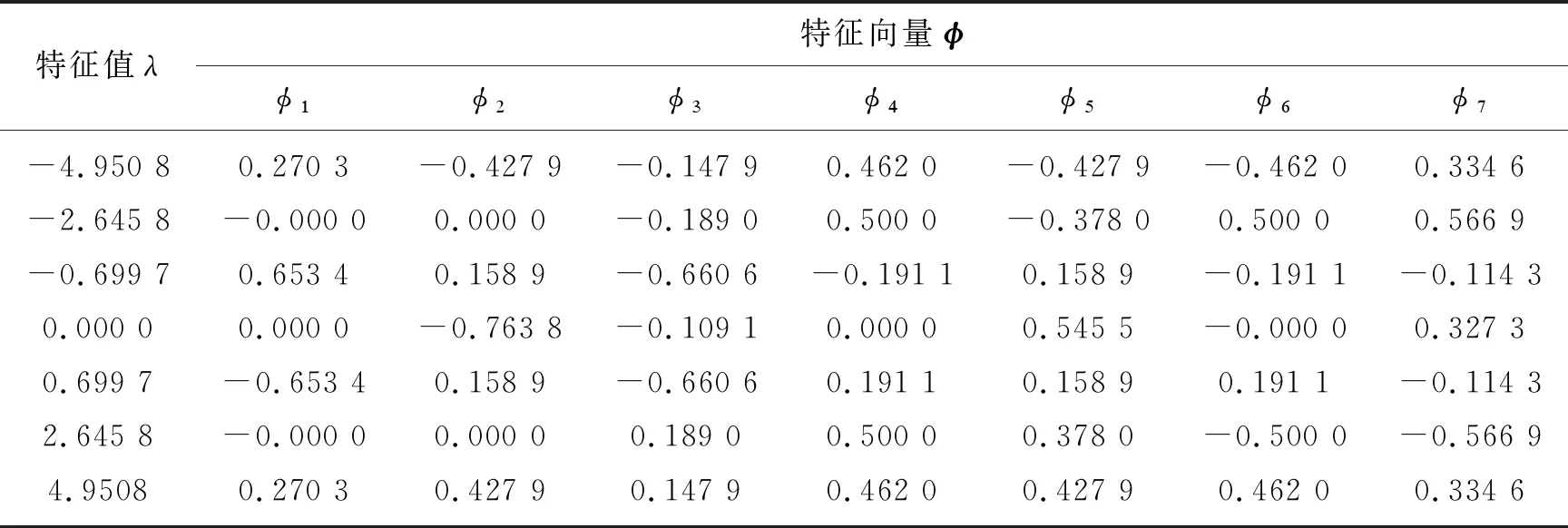
表2 邻接矩阵AC2的特征值和特征向量

表3 邻接矩阵AC3的特征值和特征向量
2.2 多级行星轮系的运动拓扑描述模型
行星轮系的运动拓扑模型是反映其运动状态的特征模型。无论是单级行星齿轮传动或多级行星齿轮传动都可以分解为外啮合和内啮合两种基本运动功能单元,见图5,其中p表示行星轮、s表示太阳轮、r表示内齿圈、c表示行星架。

图5 行星齿轮基本运动单元
以每个基本运动单元转化为定轴轮系后的传动比为特征,根据行星齿轮机构中基本运动单元内各构件的运动关系建立其转速方程:
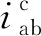
3 运动分析实例
为了验证多级行星轮系结构与运动拓扑模型的图形符号描述新方法的有效性和简单直观性,以图6(a)所示的复式行星齿轮机构为例进行运动学实例分析。复式行星传动系统由复式太阳轮2、复式行星架3、复式行星轮4、复式内齿圈5、复式双联行星轮6和6′和太阳轮7组成,其动力传递分为两路:一路为复式行星架3带动复式行星轮4、复式双联行星轮中的行星轮6与分别与复式内齿圈5和复式太阳轮2啮合传动;另一路为复式行星架3带动复式双联行星轮中的行星轮6′与太阳轮7啮合传动。通过建立其运动拓扑模型,并进行基本运动单元划分,分别对各构件的转速ω以及系统的总传动比进行求解。
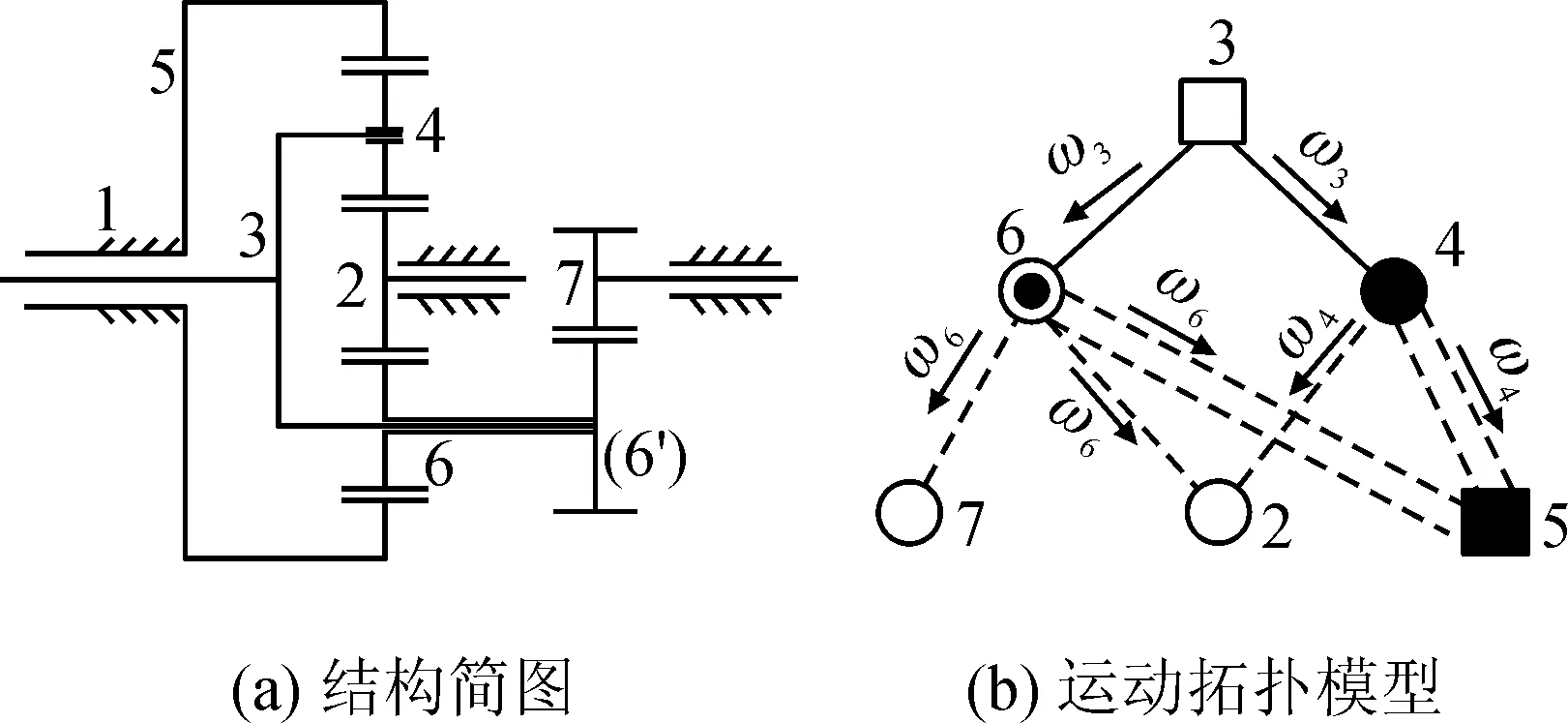
图6 复式行星齿轮传动机构
根据图6(b)中的运动拓扑模型可知,其基本运动单元为:1(3-4-5)、2(3-4-2)、3(3-6-5)、4(3-6′-7)。根据式(5),建立轮系的角速度约束方程:
(6)
式中:ωin表示复式行星架的输入角速度。将式(6)写成矩阵的形式:
(7)
倘若取复式太阳轮2、复式行星轮4、复式双联行星轮6和6′、复式内齿圈5和太阳轮7的齿轮齿数分别为Z2=12、Z4=14、Z5=40、Z6=14、Z6′=16和Z7=20,复式行星架的输入转速ωin=18 r/min,则其转速方程为:

(8)
根据非齐次线性方程组理论,利用MATLAB计算出各构件的转速如下:ω2=78 r/min,ω3=18 r/min,ω4=-33.428 6 r/min,ω5=0 r/min,ω6=-33.428 6 r/min,ω7=59.142 9 r/min。传动比i=ω7/ω3=3.285。分析结果与转化机构法计算的结果一致[22]。
4 结 论
在现有的研究成果基础上,提出了描述多级行星轮系结构特征与运动特性信息的新图形符号表示,基于新图形符号建立了多级行星齿轮的结构拓扑模型和运动拓扑模型,实现了多级行星齿轮机构与拓扑模型的一一对应关系。运动拓扑模型揭示了组成运动回路的各构件之间的运动关系和系统整体的运动特性,根据行星轮系的基本运动单元,并结合非齐次方程组理论快速简洁地求出轮系中各个运动学参量,有利于对行星轮系传动性能系统化的研究。该图形描述方法能够清晰且完整地表达各构件的属性和拓扑关系,将计算机无法识别储存的行星齿轮机构转换成可识别储存的数字邻接矩阵,有利于进行行星轮系的创新和综合。

