特殊图类的生成树数目
(湖南工业大学 理学院,湖南 株洲 412007)
0 引言
在实际应用当中,只要是描述两个事物之间的关系,均能够将其抽象概括为图论中的模型。有关图的生成树数目问题,涉及多个领域且极具实践应用价值,从而是图论研究中十分活跃的课题之一。例如,在网络系统的应用中,图(网络)生成树的数目是评估图可靠性的一个重要指标。对于一个通信网络而言,其可靠性主要由生成树的个数决定。因此,在网络可靠性的研究中,人们十分关心一个图(网络)生成树的数目问题。研究图生成树的计数对网络的可靠性研究有着十分重要的现实价值。
计算一个图的生成树数目不是件容易的事情。文献[1]利用 Feussner 公式计算了一些特殊图类的生成树数目。文献[2]通过Cayley 公式求出了3 类特殊平面图的生成树数目,并且给出了它们的递推关系式及通项表达式。文献[3]通过引入收缩团,探讨了完全图的生成树数目问题,并利用归纳法得到了比Cayley 公式更一般的公式。文献[4]给出了上述公式的概率求法。文献[5]将图的生成树数目问题归结为其块图的生成树数目问题,从而提供了一种较简便的计算图生成树数目的方法。文献[6-9]利用平面图的对偶图的Kirchhoff 矩阵,求出了一些特殊图类的生成树数目。
1 预备知识
定义1包含图G所有顶点的子图称为图G的生成子图,若图G的一个生成子图T恰为一棵树,则称T是图G的一棵生成树。图G的生成树数目用τ(G) 表示[10]。
定义2设图G是一个平面图的平面嵌入,则G的对偶图G*定义为:对于平面图G的每个面f都有G*的顶点f*与之对应,对于G的每条边e都有G*的边e*与之对应,且G*中顶点与被e*连接,当且仅当G中的面f1与f2被边e所分隔[10]。
定理1(矩阵树定理)图G的生成树数目等于其Kirchhoff 矩阵K(G)的任何一个(n-1)级主子式的值,即τ(G)=detKr(G)。其中:K(G)=D(G)-A(G),D(G)为度矩阵,A(G)为G的邻接矩阵;Kr(G)为K(G)的任何一个(n-1)级主子阵[11]。
定理2设平面图G的平面对偶图为G*,则τ(G)=τ(G*)[11]。
2 主要结果与证明
定义3设P=u0u1u2…un和Q=v0v1v2…vn(n≥1)是两条长度为n且顶点互不相交的路,则称并图为梯形图,记为Ln。将3个两两互不相交的梯形图分别与三角形的每条边的两端点相接,得到的图称为Y 形图,如图1所示,记为Yn。

图1 Y 形图Fig.1 Y-shaped graph
定义4设P=u0u1u2…unv和Q=v0v1v2…vnv(n≥1)是两条终点相同,但起点以及内部顶点不交的路,则称并图为箭形图,记为Sn。将4 个两两互不相交的箭形图分别与四边形每条边的两端点相接,得到的图称为十字形图,如图2所示,记为Tn。
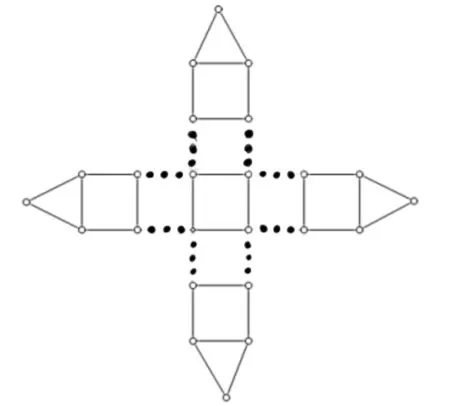
图2 十字形图Fig.2 Cross graph
定理3对n≥1,有
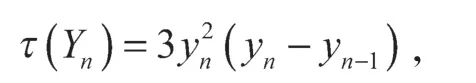
证明根据图Yn的特征可知,其对偶图Y*n是有3n+2 个顶点的平面图,且Y*n的Kirchhoff 矩阵为3n+2 阶矩阵。对Y*n的顶点进行适当标号,使其对应的Kirchhoff 矩阵为

由定理1 知,图Y*n的生成树数目等于的3n+1 阶顺序主子式,即


其中yn=4yn-1-yn-2,且y1=4,y2=15。
递推关系式yn- 4yn-1+yn-2=0 的特征多项式及其因子分解为
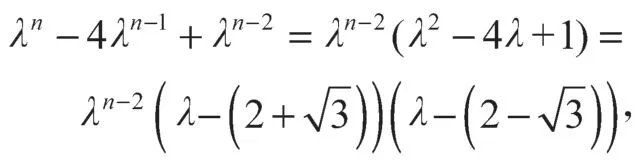
因此
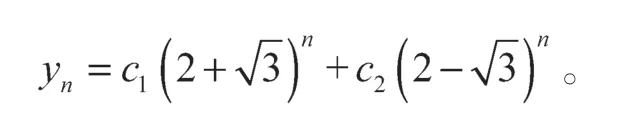
将y1=4,y2=15 代入yn得
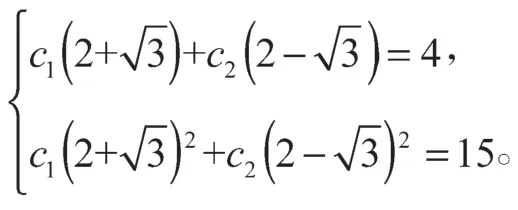
解得
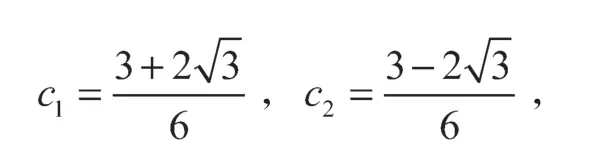
因此
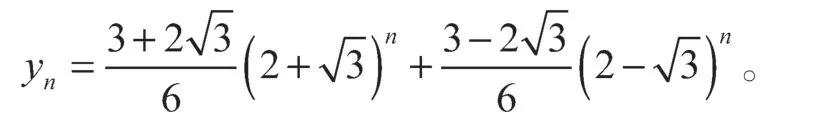
再由定理2 得
定理4对n≥1,有

证明根据图Tn的特征可知,其对偶图T*n是有4n+6 个顶点的平面图,且T*n的Kirchhoff 矩阵为4n+6 阶矩阵。对T*n的顶点进行适当标号,使其对应的Kirchhoff 矩阵为

由定理1 知,图T*n的生成树数目τ等于的4n+5 阶顺序主子式,即


将t1=3,t2=11 代入tn得
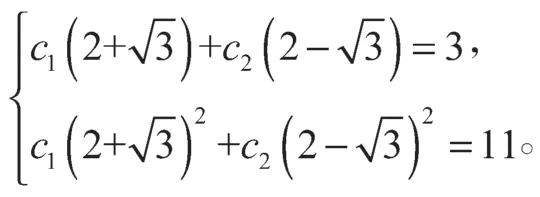
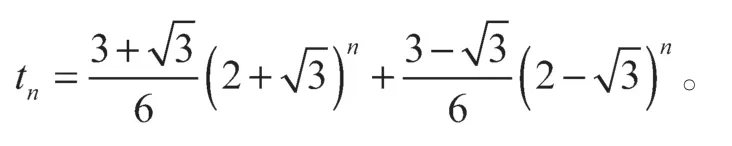
再由定理2 得
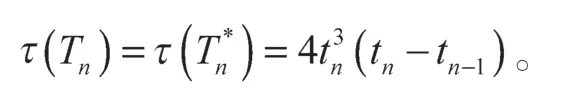
3 结语
从理论上说,可以利用Kirchhoff 矩阵树定理来确定任何图的生成树数目,但是对于一个高阶的一般图,计算其Kirchhoff 矩阵的主子式相当困难。利用Kirchhoff 矩阵树定理,结合平面图的对偶图对应的Kirchhoff 矩阵,本文的定理3 和定理4,给出了两类具有一定对称性的平面图Yn和Tn的生成树数目的通项公式,从而大大简化了对生成树数目的计算。

