剪力键高度对蜂窝空腹楼盖承载力的影响
(湖南工业大学 土木工程学院,湖南 株洲 412007)
1 研究背景
钢-混凝土组合空腹夹层板,是基于钢筋混凝土空腹夹层板理论提出的一种新型空间网格结构组合板,这种结构充分利用了混凝土良好的抗压性能及钢良好的抗拉性能,在民用、工业、桥梁结构中得到了广泛的应用[1]。钢筋混凝土空间网格结构包括平板型的空腹网架结构、空腹夹层板结构、空腹双重网格结构、现浇混凝土空心大板楼盖结构,其结构具有“安全、合理、经济、先进”性[2]。自从1995年贵州大学空间结构研究中心发明了空腹夹层板楼盖结构,至今已成功被应用于多个实际工程[3],这些实例都证明了空腹夹层板楼盖结构受力性能优越。
空腹夹层板是新型板系空间结构,可以理解为是通过“键”(竖杆)连接的双重密肋网格结构[4],可以组成密肋楼盖、双向密肋楼盖、单向密肋楼盖以及井字楼盖,其平面布置方式有正交正放、正交斜放、斜交斜放等[5]。姚玲等[6]以高跨比和组成空腹夹层板构件的主要刚度(表层板、上肋、下肋等)为参数,对空腹夹层板的静力性能进行了分析。马克俭院士提出了正六边形蜂窝空腹夹层楼盖形式,该结构和周边密柱可以形成多边大跨度空间结构,不仅满足节约资源、成本低、性能高、结构美观的原则,而且其受力性能也较为优越。李莉[7]对蜂窝型钢筋砼空腹夹层板进行了试验分析,并以工程实例实行了1/3 的缩尺模型试验,试验结果表明,在竖向荷载作用下,该结构的破坏形式为弯曲破坏,且塑性区域与破坏形式类似于实心板;结构的延性、整体性较好,刚度、承载力较大,安全度高达2.0 以上。李莉等[8]对正六边形多层大跨度公共建筑混凝土蜂窝型空腹夹层板楼盖结构进行了研究,发现该结构可以满足公共建筑楼盖平面形式多样化的要求,并且在正六边形平面中,可以将该结构看成一块类似圆形平面的夹芯板,在考虑剪切变形的情况下,证明了混凝土蜂窝型空腹夹层板结构是一种刚度好、自重轻、用材省的“性价比”较高的结构形式。赵才其等[9]对新型装配式蜂窝空腹屋盖结构的承载力进行了试验研究,其研究结果表明,若要充分发挥蜂窝板轻质高强的特性,必须要采取有效措施确保连接件不能先于蜂窝板的压屈或强度破坏。蜂窝型钢空腹夹层板剪力键节点是典型的三向受力节点,徐增茂等[10]对其屈曲稳定性进行了分析。徐金涛等[11]对蜂窝型钢筋混凝土空腹夹层板中上下肋对挠度的影响进行了分析。研究结果表明,肋高、肋宽与结构的挠度呈指数关系,挠度随着肋高、肋宽的增大而下降,并发现肋高比肋宽对结构的竖向承载力影响更加显著。在《组合结构设计规范》JGJ 138—2016 的4.3 中规定,对于l0大于9 m 时,组合楼板的挠度限值为l0/300(l0/400),这说明楼盖的刚度和楼盖承载力息息相关。
通过上述分析不难发现,在现有对蜂窝型空腹夹层板的研究中,对混凝土结构方面的研究较为完善,但对钢-混凝土蜂窝型空腹夹层楼盖的结构形式未进行深入研究;另外,在剪力键高度对蜂窝型空腹夹层楼盖承载力的影响方面的研究也并不深入。因此,本文拟对上下肋为钢T 型截面梁、剪力键为环形截面钢、楼面板为混凝土板的钢-混凝土蜂窝空腹夹层楼盖进行ANSYS 有限元分析,重点为在竖向均布荷载的作用下,通过观察楼盖竖向挠度的变化,研究剪力键高度变化对楼盖承载力的影响。
2 基本模型
2.1 工程概况
正六边形蜂窝型钢-混凝土空腹夹层楼盖是由上下两部分组成的,上部是混凝土板,下部是由上下肋钢结构梁、剪力键组成的空间钢结构梁。其中混凝土板厚度为100 mm;上下肋均为T 型截面钢梁,其截面尺寸宽×高×腹板厚×翼缘厚为T 300 mm×250 mm×12 mm×16 mm,剪力键为圆环形截面钢,截面尺寸外直径×厚度为Φ 400 mm×12 mm。剪力键高度定义为上肋的上表面到下肋的下表面间的距离,其网格构造如图1所示。
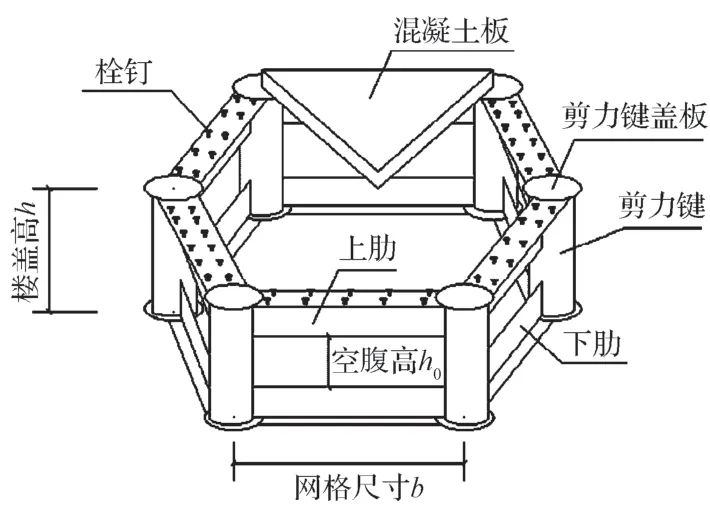
图1 蜂窝型楼盖网格构造示意图Fig.1 Cellular floor grid structure
楼盖结构的建筑总平面形状是正六边形形状,由多个边长为2 m 的正六边形蜂窝型单元组成。在有限元分析中,表层板采用SHELL181 单元,上下肋梁及剪力键采用BEAM188 单元[12],具体的材料参数及截面尺寸如表1所示。
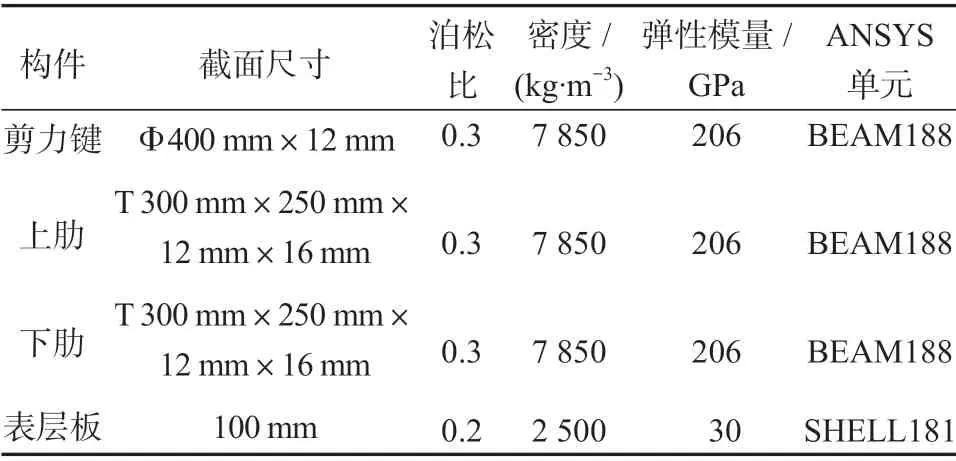
表1 各构件参数及单元选用Table 1 Component parameters with the unit selection
为了有效研究正六边形蜂窝型钢-混凝土空腹夹层楼盖,在竖向均布荷载的作用下,综合考虑其挠曲线状态以及受力性能的优越性,本研究中建立了总平面布置为边长为16 m 的正六边形,但是楼盖网格采用若干个边长为2 m 的正方形,即在仅仅改变网格形式而其余条件均一致的情况下,建立了正六边形正交正放正方形钢-混凝土空腹楼盖的对比模型,以进行对照分析。
为进一步深入研究剪力键高度对楼盖承载力的影响,本文建立了5 组算例模型,所建5 组算例的平面布置图分别为8,10,12,14,16 m 的正六边形,其长跨、短跨的长度见表2。
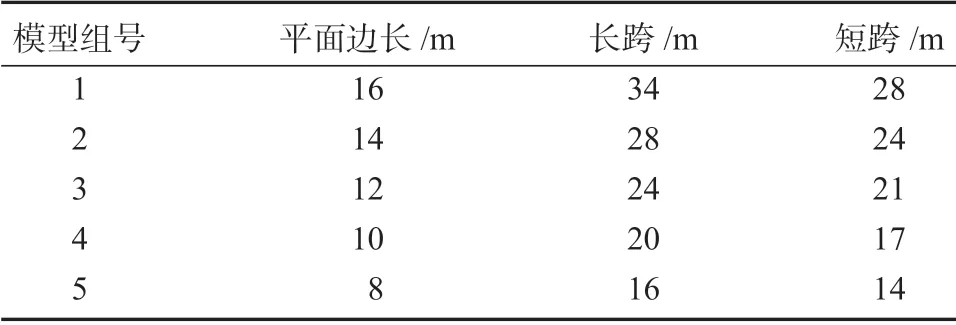
表2 平面布置跨度尺寸表Table 2 Layout span size table
以边长为16 m 的模型为例,构建如图2所示的平面布置图(图中尺寸单位为mm),其长跨为34 m,短跨为27.7 m,网格边长为2 m,材料参数以及截面尺寸如前文所述,详见表1。对每组特定的模型,在保持其他参数不变的情况下,仅改变剪力键高度,通过观察楼盖竖向挠度的变化情况,研究其静力变化。
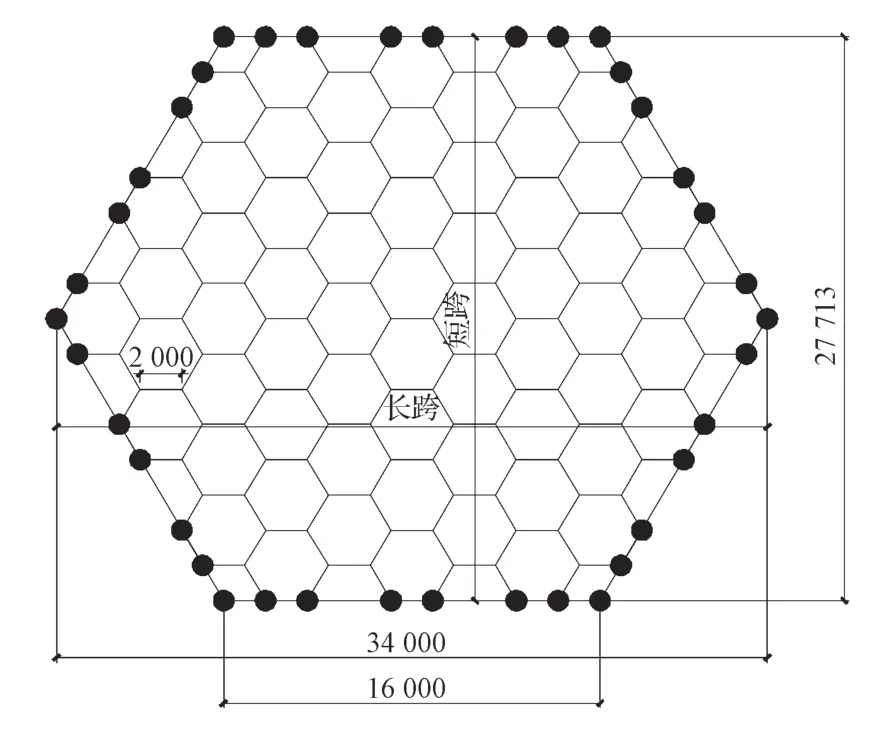
图2 第1 组模型平面布置图Fig.2 Group 1 model layout plan
本研究中对上下肋截面梁采用梁有限单元进行划分,上下肋梁各划分为20 个有限单元,剪力键也采取梁单元划分,每隔0.1 m 划分一个单元。第1 组模型中,剪力键高度为1.15 m 的模型网格划分图如图3所示。

图3 第1 组剪力键高1.15 m 算例的模型网格划分图Fig.3 Mode meshing diagram of group 1 with a shear bond height of 1.15 m
在各组楼盖模型中,对楼盖模型底部周边进行铰支约束,即在楼盖底部周边施加XYZ方向的位移约束为0,在平面图中,即图2中黑点处楼盖底部进行XYZ方向的大小为0 的位移约束[13];对整个楼面板施加8 kN/m2的竖向面荷载及由程序自行计算的自重荷载。以第1 组模型中剪力键高度为1.15 m 的算例为例,其边界条件及荷载如图4所示。

图4 第1 组剪力键高1.15 m 算例的模型边界条件及荷载图Fig.4 Model boundary conditions with the load diagram of group1 with a shear bond height of 1.15 m
2.2 计算结果分析
图5所示为第1 组模型中剪力键高度为1.15 m 的正六边形蜂窝型钢-混凝土空腹夹层楼盖在8 kN/m2的竖向面荷载及自重荷载作用下的位移云图。由图5可知,该结构在竖向均布荷载作用下,整体变形呈弯曲变形,整体楼盖形状类似碗底形状,且跨中的挠度最大,越靠近边缘挠度越小,最大挠度为374.77 mm。
图6所示为总平面为16 m 的正六边形、网格形式为正交正放正方形、网格边长为2 m 的正方形及剪力键高度为1.15 m 的钢-混凝土空腹夹层楼盖的对比模型,在与第1 组模型剪力键高度为1.15 m 的正六边形蜂窝型钢-混凝土空腹夹层楼盖所受荷载一致情况下的位移云图。从图6可知,在竖向均布荷载作用下,正交正放的正六边形总平面布置模型的位移云图,也是跨中位移最大,越往边缘有约束的地方位移越小,整体变形形状与正六边形蜂窝型空腹夹层楼盖相近,最大挠度为278.33 mm。
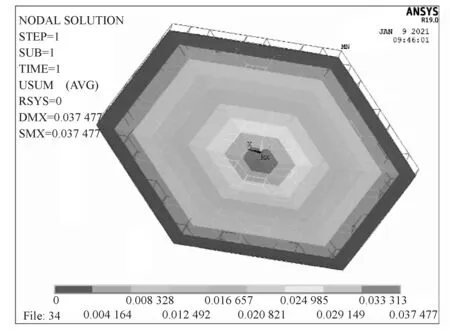
图5 第1 组剪力键高1.15 m 算例的模型位移云图Fig.5 Model displacement cloud diagram of group 1 with a shear bond height of 1.15 m
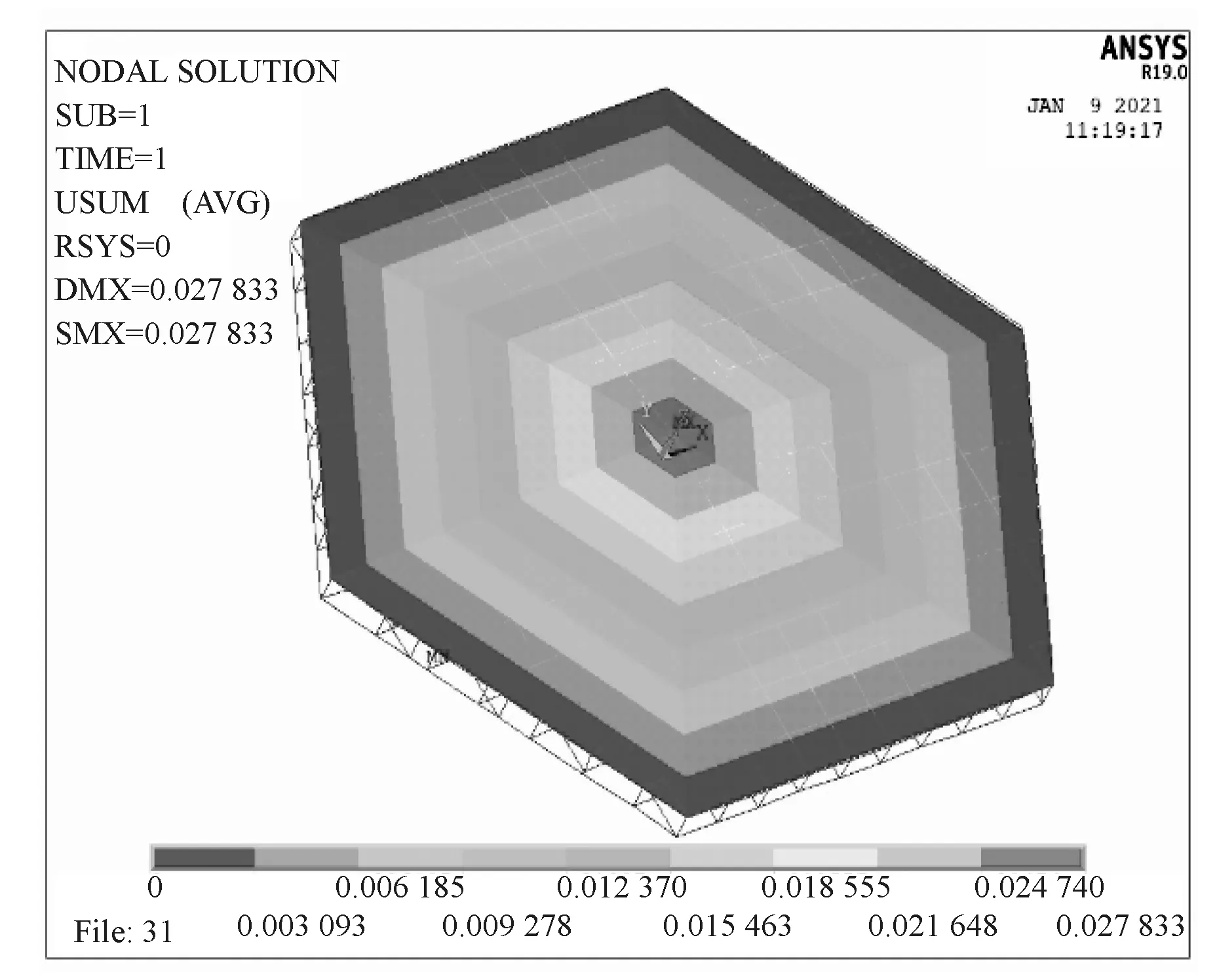
图6 对比算例位移云图Fig.6 Displacement nephogram of contrast examples
对比图5和图6可以得知,两者的挠曲状态、受力性能相近。在正六边形总平面布置、网格边长相同的情况下,由正交正放的矩形网格所组成的空腹夹层楼盖承载力略优于由蜂窝型网格所组成的空腹夹层楼盖承载力。但是当计算这两个模型用钢量时可以发现,正六边形蜂窝型空腹夹层楼盖使用了2 m 一根的 T 300 mm×250 mm×12 mm×16 mm 截面梁上肋295 根,下肋295 根,总共590 根,共1 180 m 长的该截面钢梁,160 根1.15 m 长的Φ 400 m×12 mm环形截面钢剪力键;而正六边形正交正放空腹夹层楼盖共使用了767 m 的上肋钢梁及678 m 的下肋钢梁,共1 534 m 长的T 300 mm×250 mm×12 mm×16 mm截面钢梁,222 根1.15 m 长的Φ400 mm×12 mm 的环形截面钢剪力键。正六边形正交正放空腹夹层楼盖相较于正六边形蜂窝型空腹夹层楼盖的组合梁用钢量提升了30%,但挠度只下降了25%。因此在仅改变网格形式,而总平面布置相同、蜂窝型边长和正交正放正方形边长相同及其他条件相同的情况下,正六边形蜂窝型钢-混凝土空腹夹层楼盖相较于正交正放矩形网格的钢-混凝土空腹夹层楼盖更加经济。
为进一步研究剪力键高度对正六边形蜂窝型空腹夹层楼盖承载力的影响,对上述提到的5 组模型进行分析与研究。每组在仅改变剪力键高度的情况下,施加相同的荷载,得到对应的最大位移,并以最大挠度为纵坐标、剪力键高度为横坐标,将每组数据点各自连接起来,绘制成图7。因这几条曲线趋势图的趋势相同,为具体看出挠度随着剪力键高度变化的趋势图,取第4 组的曲线单独为例成图,如图8所示。
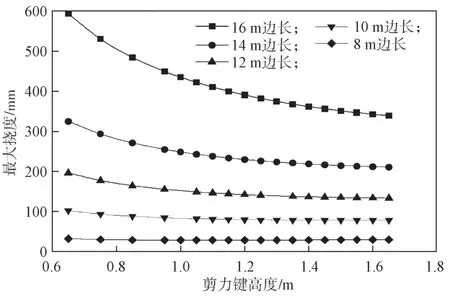
图7 第1~5 组最大挠度随剪力键高度变化曲线Fig.7 The trend graph of the maximum deflection of groups 1~5 with the height of the shear key

图8 第4 组最大挠度随剪力键高度变化曲线Fig.8 Curve of the maximum deflection of group 4 with the height of the shear key
如图7所示,随着剪力键高度的增加,在自重以及8 kN/m2面荷载的作用下,楼盖的最大挠度不断减小,由此可以证明,提高剪力键高度可以提高楼盖的刚度。
由图8可得,在其他条件不变的情况下,随着剪力键高度的提升,挠度先是迅速减小;当继续增加时,挠度减小速度减缓;但当超过一定范围后,挠度不减反增(具体数据如表3所示)。

表3 第4 组最大挠度反增数值表Table 3 Maximum deflection inverse increment table of group 4
这是由于当剪力键高度提高时,楼盖高度得到了提高,进而提升了楼盖的刚度;在提升相同剪力键高度时,开始提高之初,楼盖刚度的刚度较小,当提升一定的剪力键高度后,提升后的楼盖刚度相较初始时的提升较多,故而随着剪力键高度的提升,挠度下降迅速;但随着剪力键高度的提高,楼盖的刚度不断提高,楼盖刚度的基数变大,因此每次所提升的刚度值相较上一次提升刚度值都有所减缓,所以随着剪力键高度的提升,挠度下降的速率减缓;但当剪力键高度提升到一定程度后,剪力键更容易发生屈曲和失稳,因此再提升剪力键高度会使得楼盖的挠度不增反减。
取相同的剪力键高度,依次取每组对应的最大位移值,以最大挠度为纵坐标,每组平面边长为横坐标,作出挠度随正六边形平面边长变化趋势图,见图9。
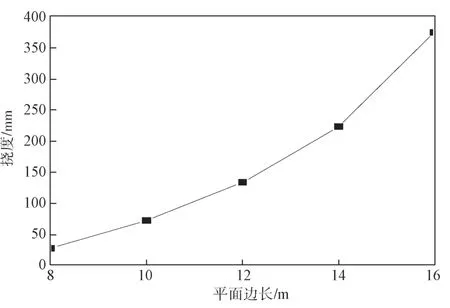
图9 挠度随总平面边长变化曲线Fig.9 Trend chart of deflection with the side length of the total plane
由图9可知,随着正六边形平面边长的增加,楼盖的挠度增加,并且增加得越来越快。这是由于,随着正六边形平面边长的增加,整个楼盖的跨度相应增加,故而其刚度有所下降,所以在相同的剪力键高度的情况下,随着平面边长的增加,挠度会随着增加。
因各组挠度随剪力键高度变化曲线趋势类似,为研究其共同性质,通过计算拟合发现,当取挠度为纵坐标,剪力键高度与总平面边长的比值为横坐标做图,它们的变化趋势皆一致,故取第5 组为例,其变化曲线如图10所示。
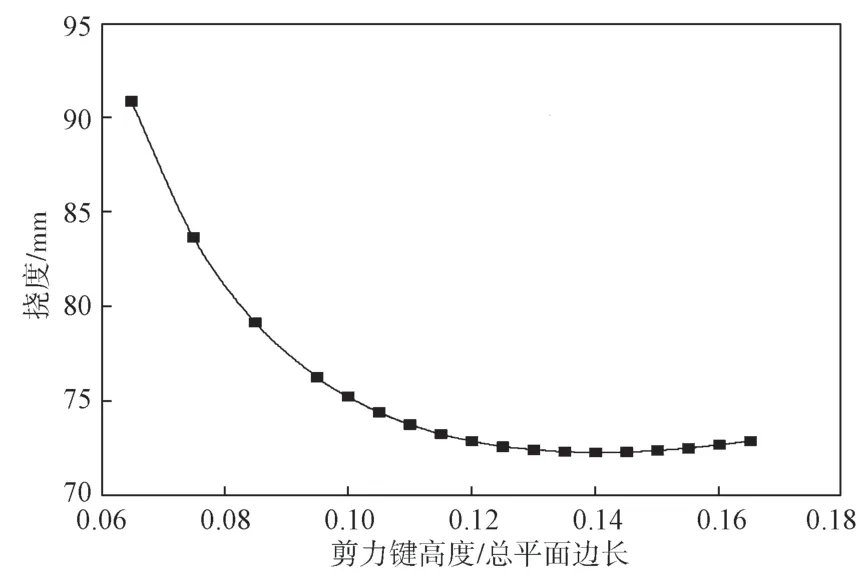
图10 第5 组挠度随剪力键高度/总平面边长的变化曲线Fig.10 Deflection curve with shear key height/total plane side length of group 5
由图10可以看出,在剪力键高度/总平面边长比值小于0.12 时,提升剪力键高度,可以有效提升楼盖刚度,且在剪力键高度较小时,刚度提升更为明显,随着剪力键高度的提高,刚度提升效率减缓;当该比值介于0.12~0.135 之间时,发现提升剪力键高度,对楼盖刚度有一定提升,但提升效果不佳;当该比值超过0.135 之后,发现继续提升剪力键高度对楼盖承载力甚至有不利影响。
因此,在使用上下肋为T 型钢、剪力键为环形钢、受压板为混凝土板的钢-混凝土正六边形蜂窝型空腹夹层楼盖时,为了提升楼盖的刚度,可以适当提升其剪力键高度,但是建议不要超过正六边形总平面边长的0.135 倍。
3 结论
1)上下肋为T 型钢、剪力键为环形钢、受压板为混凝土板的钢-混凝土正六边形蜂窝型空腹夹层楼盖的受力性能良好,在受均布荷载的情况下,其跨中挠度最大,且受力性能与用材一致的正交正放空腹夹层楼盖相近。
2)对于此类空腹夹层楼盖,平面布置形式采用蜂窝型的结构刚度相较于采用正交正放正方形结构刚度相近且稍微小一些,但平面布置为蜂窝型的空腹夹层楼盖结构的经济性明显优于采用正交正放正方形平面布置的空腹夹层楼盖结构的经济性。
3)对于此类正六边形蜂窝型空腹夹层楼盖,当剪力键高度不变时,增加楼盖平面边长,会增加其跨度,导致其刚度降低。
4)在此类正六边形蜂窝型空腹夹层楼盖中,当剪力键高度/总平面边长的比值小于0.12 时,增加剪力键的高度可以有效地提升楼盖承载力;但当剪力键高度/总平面边长的比值大于0.135 时,继续提升剪力键的高度对楼盖结构承载力收益不高,甚至有不利影响。

