高速无位置无刷直流电机控制系统的精确换相仿真研究
易佩华,陈卫兵,钟德刚
(1.湖南工业大学 计算机与通信学院,湖南 株洲 412007;2.杭州欣易达驱动技术有限公司,浙江 杭州 310008)
1 研究背景
无刷直流电机(brushless DC motor)具有结构简单、运行平稳、容易控制、抗干扰能力较强等优点,因而被广泛地应用于家电、仪表、高端工业设备等中[1-4]。无刷直流电机一般通过安装在电机尾端的位置传感器来检测转子位置,而位置传感器的安装会使得电机成本增加,同时也需要额外添加信号线,这会使得电机运行的可靠性降低。
无位置传感器的控制方式可以提高电机运行的可靠性及其抗干扰能力,同时也杜绝了由于位置传感器安装不准确带来的换相误差。近年来,高速段的无位置无刷直流电机的控制已经成为电机控制领域的研究热点之一[5-12]。无位置直流无刷电机的主要控制方式有反电势过零点法、三次谐波法、续流二极管法、观测器估计法等。如文献[1]重点分析了线反电势与换相时刻的对应关系,并提出减少一路电压检测电路,设计了相移补偿策略,该策略消除了传统反电势法带来的转子位置检测不准确问题,但是电机在高速状态下运行时无法确定该方法的准确性。文献[2]提出了利用芯片寄存器状态和换相电流续流时间的特性来避开脉冲宽度调制(pulse width modulation,PWM)和续流时间带来的干扰,这一改进在硬件设计上得到了简化,但是因增加了芯片的计算,会带来额外的计算延时。文献[3]对三相电压之和进行了3 次谐波检测获得过零点信号,但是该方法无法避免由续流引起的换相误差,进行深度滤波又会造成延时时间过长的问题。文献[4]根据续流二极管的工作状态,提出一种续流二极管法,但是该方法究其本质也是对绕组的反电势检测,电机需要开环启动后才能切换到该方法。文献[5]提出使用二阶滑膜观测器对无刷直流电机进行直接转矩控制。但因其对符号函数进行了积分,从而削弱了由于符号函数造成的抖振影响,且无需设置低通滤波就可以直接获得理想的梯形波反电势,但是该方法的计算量较大,对微控制单元(microcontroller unit,MCU)的要求比较高。
在上述各种无位置控制方法中,当其被应用到高速场景时,由于滤波延时、转速波动、转矩波动、MCU 计算时间等原因,会使得过零点的出现超前或者滞后,造成换相不准确,严重时可能会导致电机失步。因此,针对上述问题,本文拟在分析直流无刷电机工作原理和数学模型的基础上,采用传统的反电势过零点法,并采用电流环、速度环双闭环PID(比例-积分-微分)控制,且用单相电压和单相电流的相位差对反电势过零点进行补偿,改进无刷直流电机控制系统。最后,使用Matlab/Simulink 对该高速无位置无刷直流电机控制系统进行仿真以验证本论文提出的控制策略的有效性和可行性。
2 反电势过零检测原理
2.1 无刷直流电机数学模型
三相全桥式无刷直流电机系统的等效电路如图1所示。图中,Udc为系统母线电压,Ua、Ub、Uc分别为三相定子端电压,ia、ib、ic分别为三相定子端电流,ea、eb、ec分别为三相反电势,R为定子绕组电阻,L为定子绕组电感,M为定子绕组互感,N为电机绕组中心点,T1~T6为功率器件。
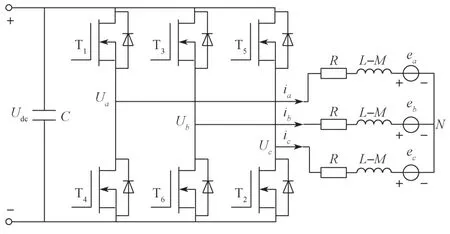
图1 三相全桥式无刷直流电机等效电路原理图Fig.1 Principle of equivalent circuit of three-phase full-bridge brushless DC motor
由于无刷直流电机的理想反电势为梯形波,电感为非线性变化,为了便于分析,结合无刷直流电机的诸多特点,做出如下假设:
1)定子绕组为60°相带整距集中绕组,且为Y型连接;
2)忽略磁路饱和,不计涡流和磁滞损耗;
3)转子没有阻尼绕组,永磁体不起阻尼作用;
4)不考虑电枢反应,气隙磁场分布为梯形波,平顶宽度为120°电角度;
5)忽略齿槽效应,绕组均匀分布于定子内表面。
根据图1,三相绕组的电压方程可以表示如下:
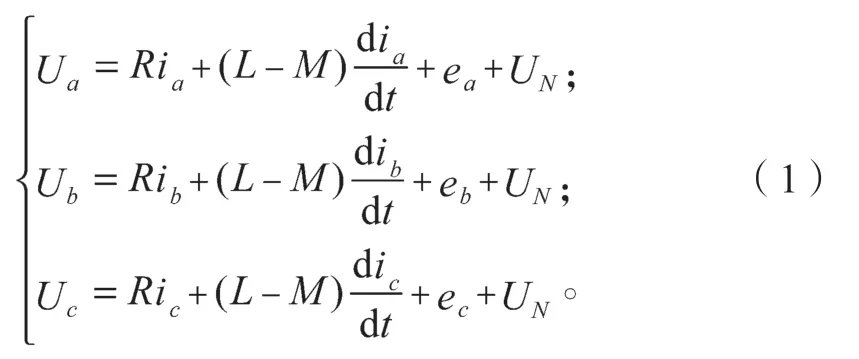
式中UN为电机中点电压。
无刷直流电机的电磁转矩方程为
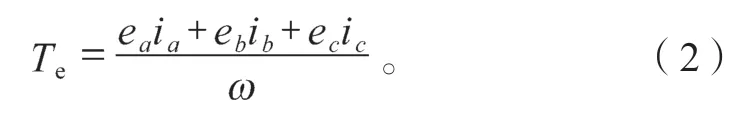
式中:Te为电磁转矩;
ω为转子机械角速度。
无刷直流电机的电机运动方程为
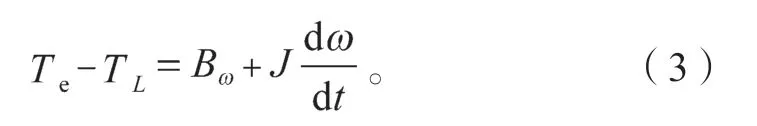
式中:TL为负载转矩;
Bω为黏滞阻尼系数;
J为转子的转动惯量。
2.2 无刷直流电机换相分析
无刷直流电机的理想反电势、相电流示意图如图2所示。图中φt为转子转过的电角度,理想情况下反电势为平顶宽度为120°的梯形波,相电流为方波。电机采用两两导通的工作方式,每60°换相一次。当反电势幅值最大时(120°平顶区域),相电流导通区与反电势幅值最大区的相位重合。如果超前换相或者滞后换相,则反电势与相电流相位之间有一相位差。图中pi对应180°电角度;Zc为滤波计算后的过零点;Zp为延时30°电角度后的过零点。
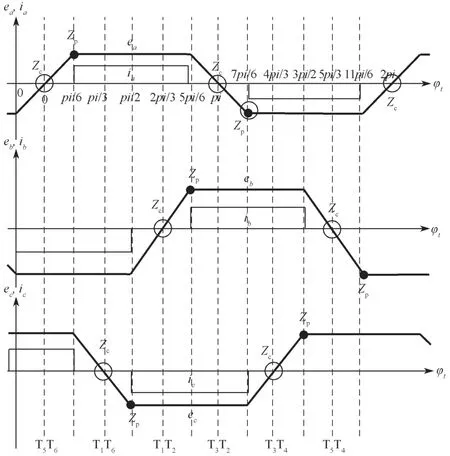
图2 理想反电势与相电流示意图Fig.2 Schematic diagram of ideal back EMF and phase current
由无刷直流电机运行时的电流特性,可以得到三相定子电流的关系式,为

将式(1)中3 个式子相加,再将式(4)所示电流关系式代入,可得电机的端电压、反电势、中点电压的关系表达式如下:
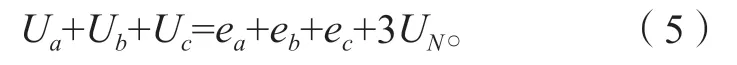
在反电势过零点时刻,导通的两相反电势的幅值相等,但方向相反,悬空相的反电势为0,由式(5)可得:
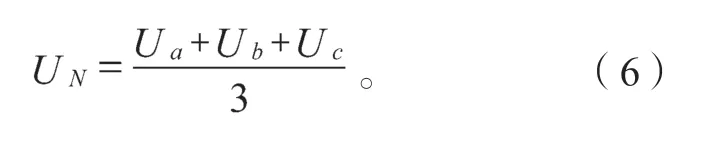
电机两两导通,悬空相的电流为0,可以将任意一相视为悬空相x,根据式(1)可以得到悬空相的电压关系式为

根据式(6)可计算出中点的电压UN,而端电压Ux可以通过测量得到。通过式(7),比较端电压与中点电压即可以得到过零点信号。过零点信号如图2中Zc所示,过零点信号延时30°电角度时间即可以得到换相信号Zp。每一次换相时的电角度周期可以根据实时转速计算得出。反电势频率与转速的对应关系式为

式中:n为电机转速;
p为电机极对数;
f为反电势频率。
根据式(9)可以计算出延时电角度φ所对应的时间。

2.3 高速状态下无刷直流电机换相分析
在理想工况下,由端电压滤波计算得到的反电势过零点,如图2中Zc所示;再延时30°电角度时间即可得到准确的反电势过零点,如图2中Zp所示;随着转速越来越大,换相时间越来越短。表1为不同转速下的换相时间。
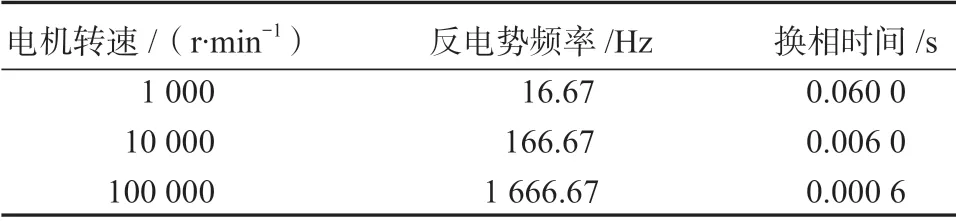
表1 不同转速下的换相时间Table 1 Commutation time at different speeds
分析表1中的数据可以得知,电机在低速区间运行时,滤波延时、转速变化、负载突变等因素对实际换相点的影响不明显,但当电机在高速状态运行时,电机换相时间和延时时间缩短。
表2所示为电机极对数p=1 时,不同转速下所对应的延时时间。
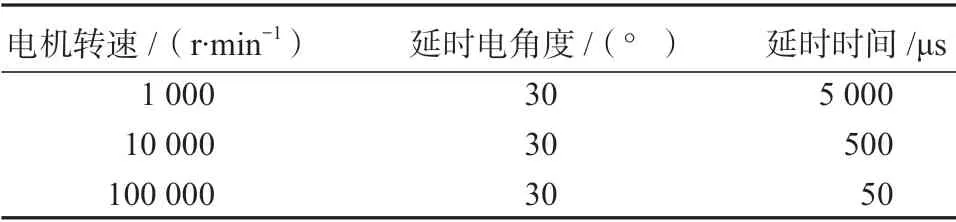
表2 不同电机转速对应的延时时间Table 2 Delay time corresponding to different speeds
由表2可知,当电机转速达到1×105r/min 时,延时30°电角度的时间为50 μs。由于实际中不仅只有滤波所带来的延时,还包括MCU 的运行时间等,所以实际延时可能会大于50 μs,这时电机转速将会低于给定转速。MCU 运行时间可以测试出来,硬件滤波延时可以通过计算得出[10],对于负载的变化,可以通过离线下测得电流续流角度和电流大小与转速的关系得出[8]。得到滤波延时和不同负载情况下的电流续流角度后,可以通过查表的方式来获取不同转速下的延时时间。
由前文给出的图2可以得知,电机在准确换相的情况下,同相的反电势幅度最大区域与导通时相电流的相位重合。
如果将反电势相位用α表示,相电流相位用β表示,并且以θ表示相位差,则这两个相位间的关系表达式为

由于反电势不能直接获取,端电压又与反电势同相位,所以用端电压相位代替反电势相位。θ越小时两者相位差越小,换相角度越准确。
3 无刷直流电机仿真系统的搭建
3.1 电机本体模块
本研究中,电机本体模块采用Simulink 库中自带的Permanent Magnet Synchronous Machine 电机模块。
3.2 反电势计算模块
以电压转换模块采集三相定子的端电压,将其经过低通滤波处理后,再根据式(1)(4)(5)(7),通过计算可以得到电机三相绕组的反电势,且根据式(6)可以计算出中点电压。最后,通过式(8)比较端电压与中点电压,得到反电势信号。本研究中构建的反电势计算模块如图3所示。
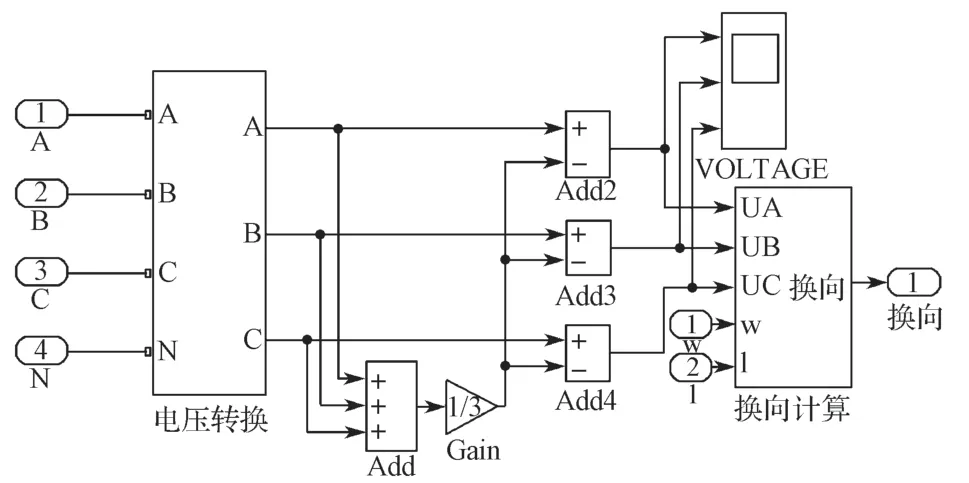
图3 反电势计算模块Fig.3 Back EMF calculation module
3.3 反电势过零点提取模块
将经过计算后得到的三相反电势信号,通过滞环比较器,分别得到三路幅值为1 的方波信号;将三路过零点信号叠加,即可得到完整的过零点信号。由于受到滤波延时、续流、转矩波动等的影响,过零点信号需要延时相应的电角度才可以得到准确的换相点。将延时后的过零点信号用累加器循环计数后,即可以得到准确的换相信号。本研究中构建的反电势过零点提取模块如图4所示。
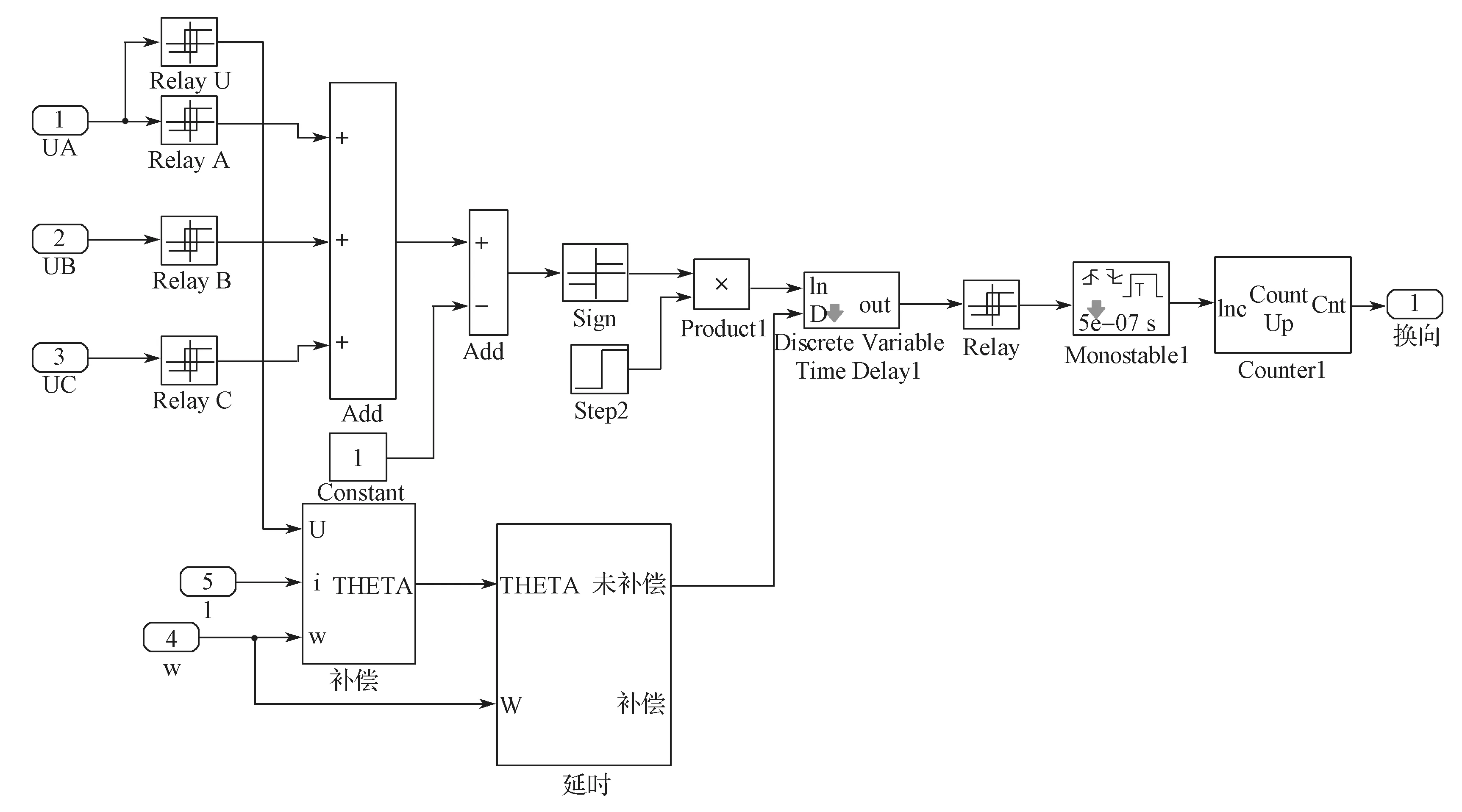
图4 反电势过零点提取模块Fig.4 Back EMF zero-crossing point extraction module
3.4 逻辑换相模块
本研究中构建的逻辑换相模块如图5所示。
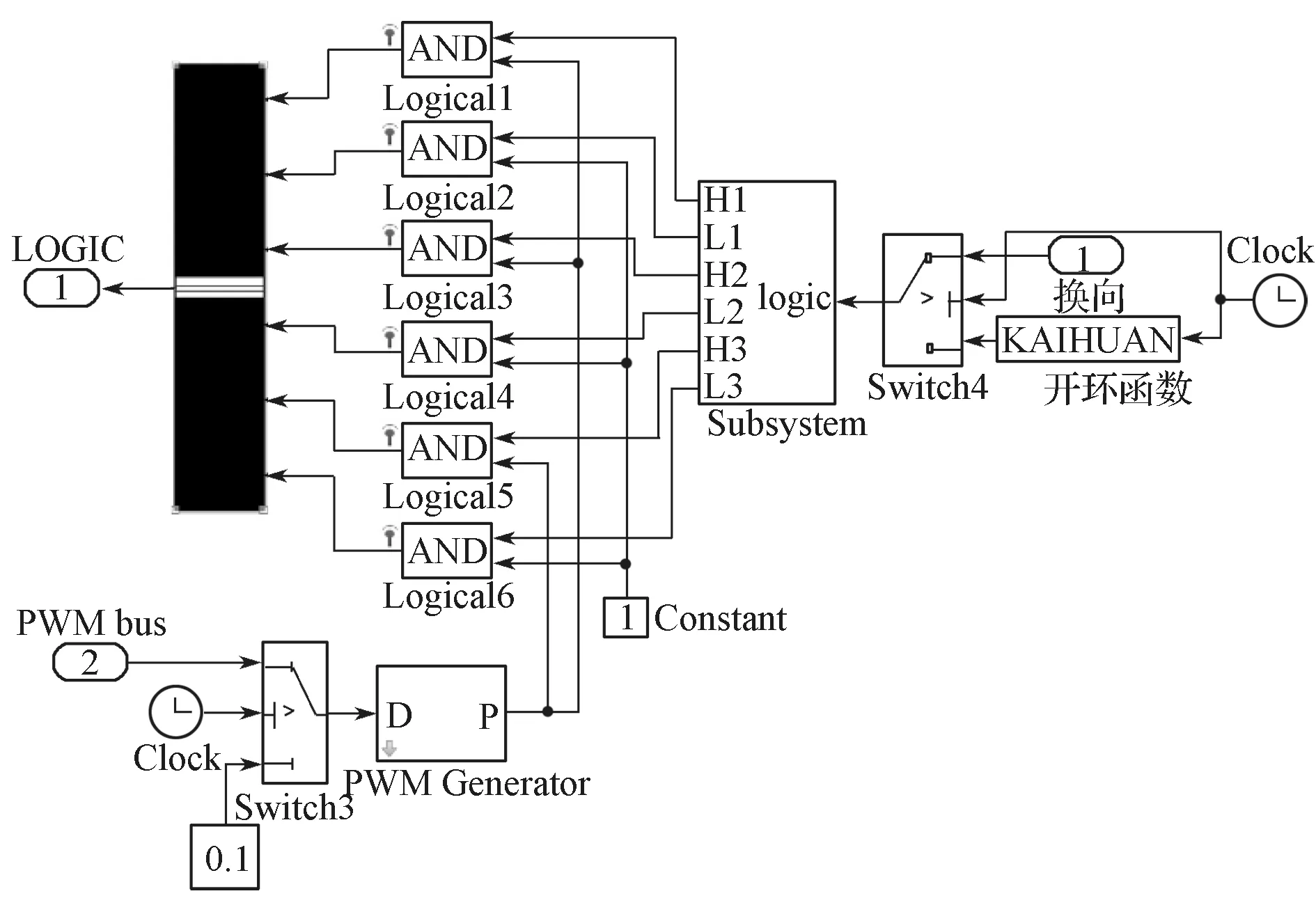
图5 逻辑换相模块Fig.5 Logic commutation module
电机启动采用传统“三段式”开环启动,调制方式为上桥调制、下桥恒通 (HPWM-LON)。开环启动时间为0.018 5 s,0.018 5 s 后切入闭环控制。PWM 模块采用Simulink 库自带的PWM Generator 模块,开环占空比为10%。
3.5 相位差计算模块
由于电机反电势不能经过直接测量得到,所以用测量得到的端电压代替反电势,端电压、相电流的频率相同,故只需要将两个相位提取出来即可。先将同相端电压、相电流经过滤波处理后,用滞环模块,将两个信号变成幅值为1 的方波信号。将方波信号代替端电压信号和相电流信号的相位,得到两者的相位差,然后可以使用公式(9),逆推得到所对应的电角度。本研究中构建的相位差计算模块如图6所示。
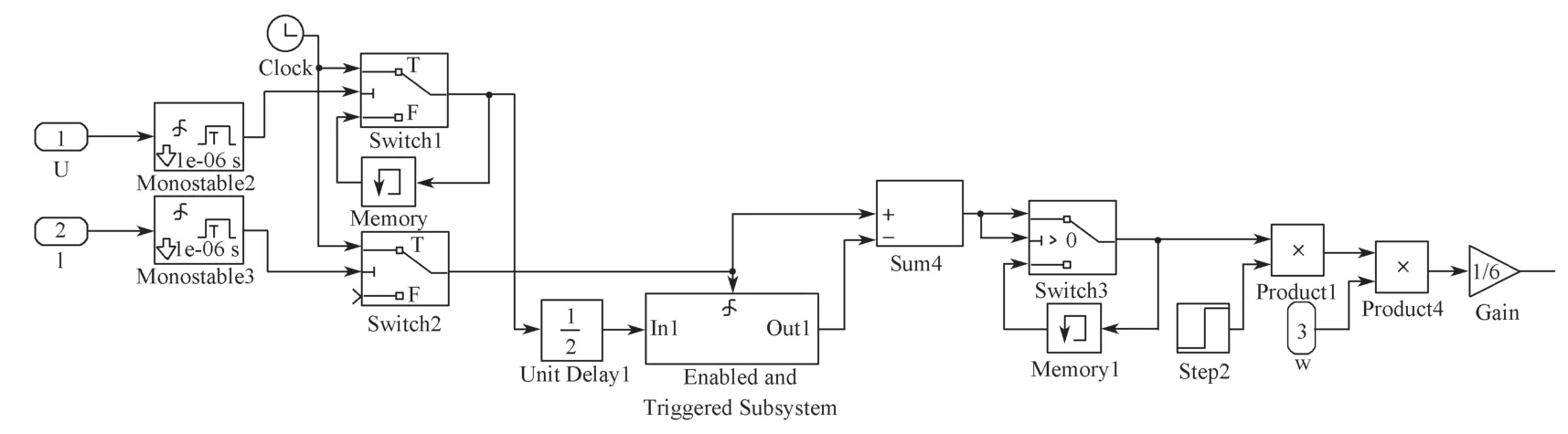
图6 相位差计算模块Fig.6 Phase difference calculation module
3.6 补偿计算模块
首先,将相位差计算模块得到的电角度与换相表中的电角度累加,得到准确的延时角度;然后根据公式(9),经过计算后得到延时时间。最后,将得到的延时时间传入反电势过零点提取模块的Discrete Variable Time Delay 延时模块中,即可以得到准确的换相信号。本研究中构建的补偿时间计算模块如图7所示。
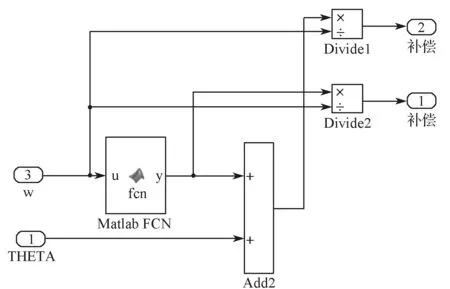
图7 补偿时间计算模块Fig.7 Compensation time calculation module
3.7 无位置无刷直流电机控制系统整体模块
将上述各模块整合,构成控制系统的整体框架。电机模块输入为不同时刻的不同转矩。本研究中无位置无刷直流电机控制系统的整体模型如图8所示。
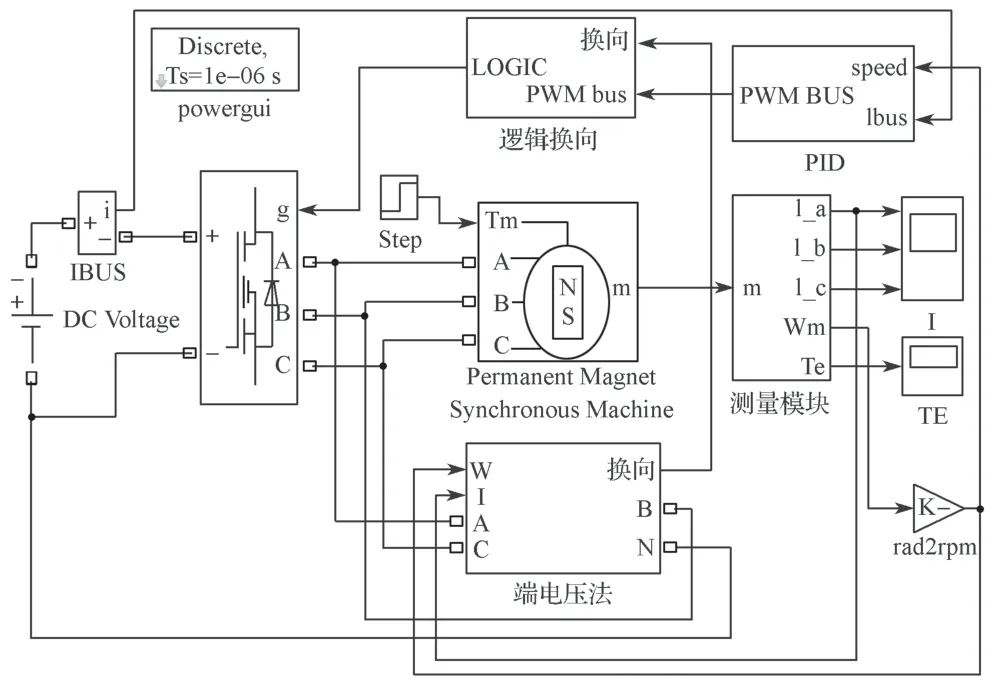
图8 无位置无刷直流电机控制系统整体框图Fig.8 BLDCM control system block diagram
4 仿真结果与分析
本研究基于Matlab/Simulink 仿真平台,建立了无位置无刷直流电机控制系统的仿真模型,并且对该模型进行了双闭环仿真分析。仿真条件和电机参数设置如下:
1)仿真条件。直流电压为24 V,PWM 频率为20 kHz,速度环PI 的参数为Kp=6、Ki=0.09,电流环PI 参数为Kp=15、Ki=5,仿真时间为0.5 s,仿真步长Ts=1e-6s。
2)电机参数。电机极对数p=1,额定电压U=24 V,额定转矩为0.04 N·m,额定转速为1×105r/min,相电阻为0.045 Ω,等效电感为15 μH,反电势系数为0.17 V·(r·min-1)-1。
为验证仿真系统的动态性能、稳态性能,系统带载启动,初始的负载转矩为0.01 N·m,给定的转速为1×105r/min,进入稳态后,进行转矩突变测试和转速突变测试。
4.1 补偿前后误差分析
仿真所得补偿前后的系统端电压与相电流相位差如图9所示。
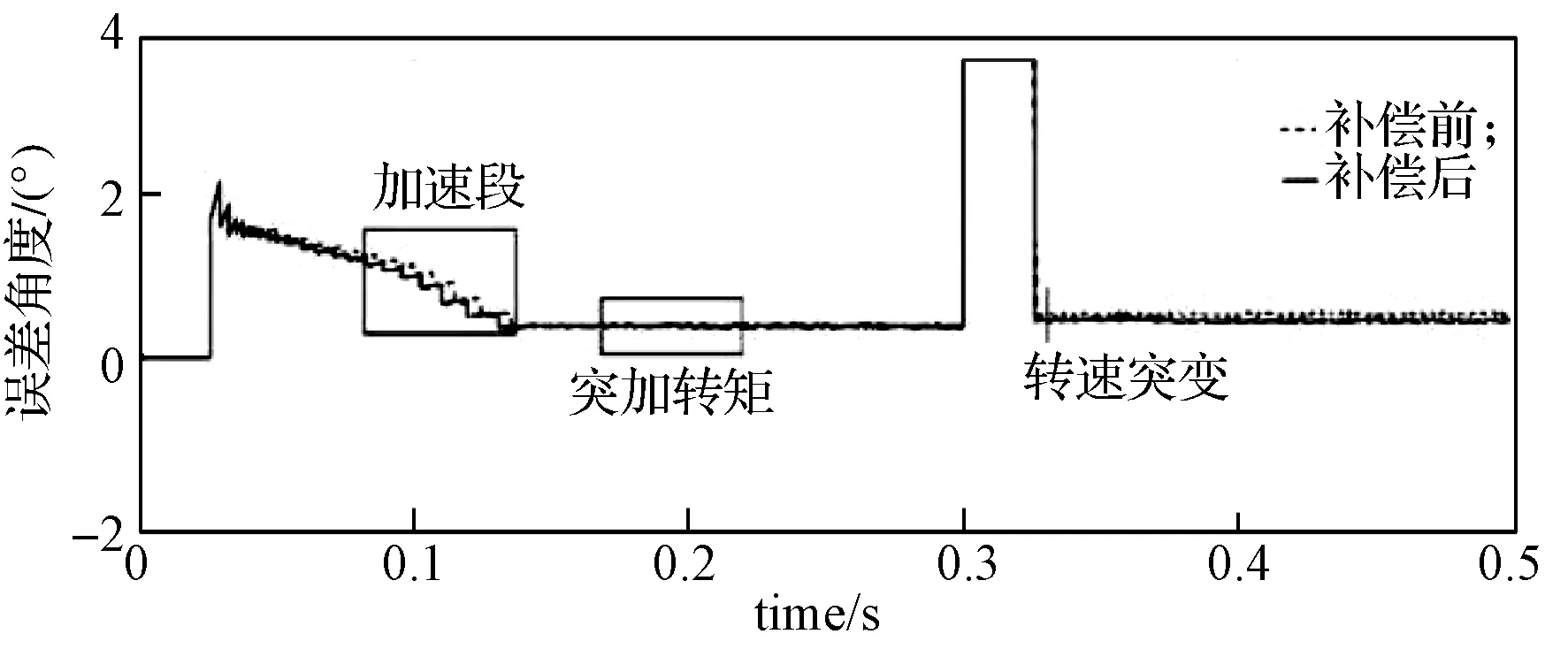
图9 补偿前后的系统端电压与相电流相位差Fig.9 Phase difference between terminal voltage and phase current before and after compensation
从图9中可以看出,加入误差补偿后,在加速阶段,其相位差明显小于未加补偿的相位差。在转矩突变和转速突变时,补偿后的相位差更小,说明其换相更加精确。
4.2 补偿前后转速分析
仿真所得系统补偿前后的转速整体对比波形如图10所示。
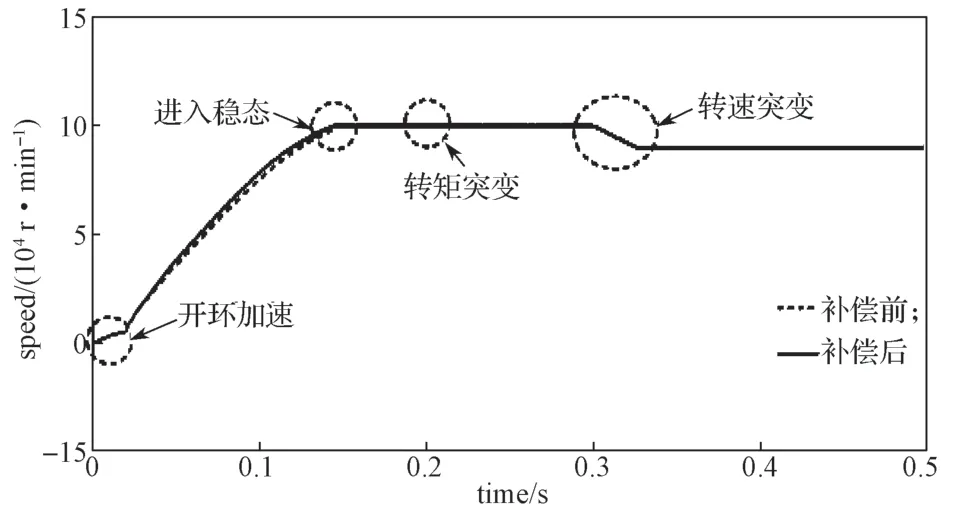
图10 系统补偿前后的转速仿真波形Fig.10 Speed waveform before and after compensation
如图10所示,经过补偿后的转速仿真波形比补偿前的更快达到给定的参考转速。
转速达到给定参考转速后,在0.2 s 时将初始负载转矩0.01 N·m 增加至0.04 N·m,并且在0.3 s 时将给定参考转速设为9×104r/min。图11为转矩突变点和转速突变点的放大仿真波形。
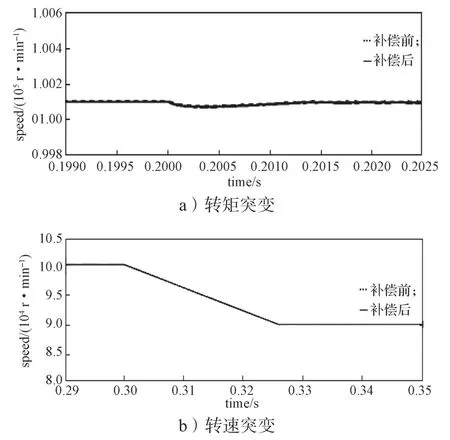
图11 转矩突变点和转速突变点仿真波形Fig.11 Simulation waveform of sudden torque point and speed mutation point
从图11a 中可以看到,在0.2 s 时突加转矩,转速有小小的凹痕波动,转速波动在0.002 s 后,重新回到给定参考转速1×105r/min。在0.3 s 时,转速给定突变到9×104r/min,系统在0.026 s 后即达到给定参考转速9×104r/min。这一结果说明,与未加补偿的系统模型相比,补偿之后的系统转速响应更加良好,抗干扰能力更强。
4.3 补偿前后电流分析
仿真所得系统补偿前后电流整体对比波形如图12所示。
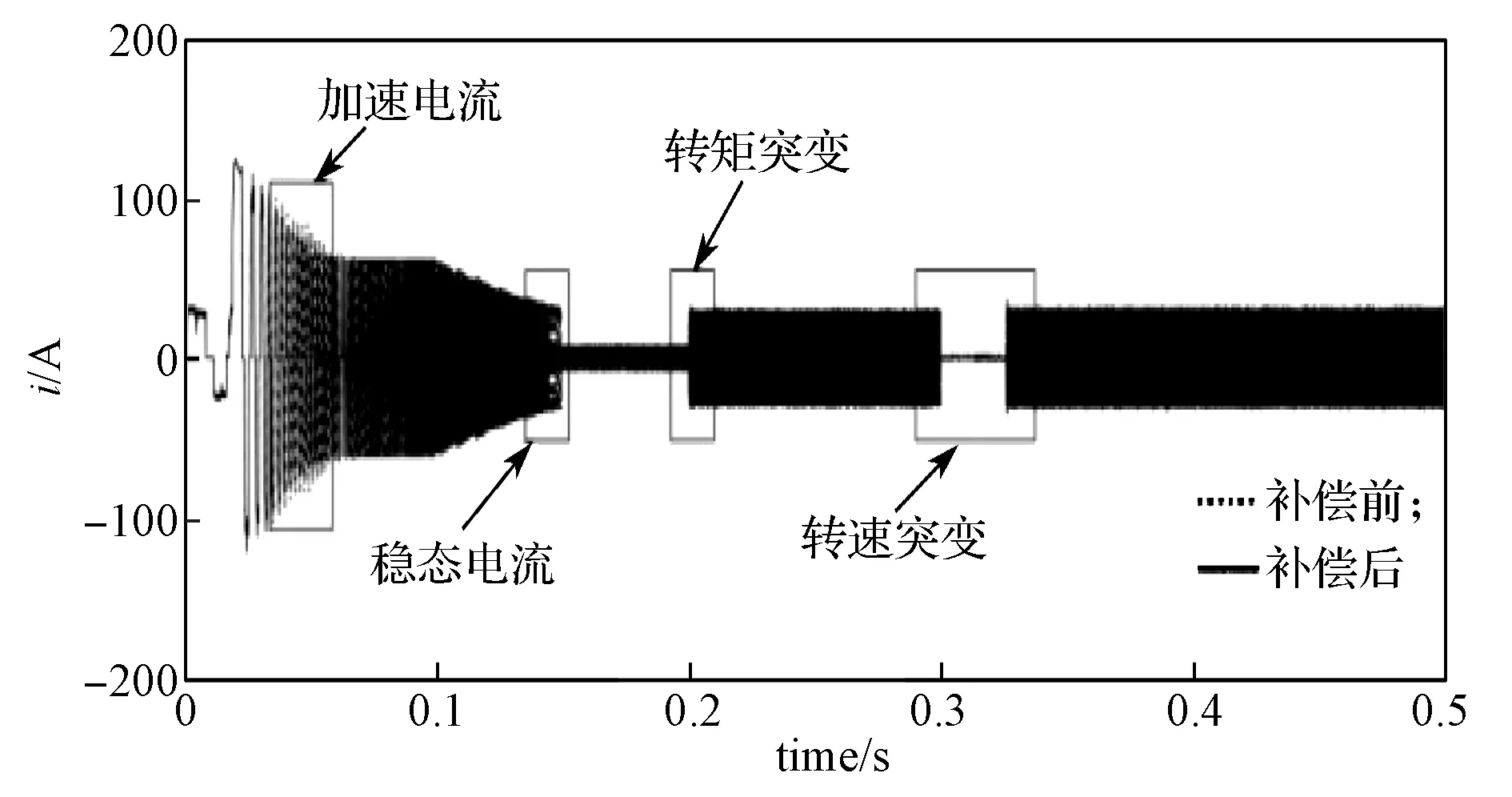
图12 补偿前后的系统电流仿真波形Fig.12 Simulation waveform of system current before and after compensation
由图12可以看出,控制系统经过补偿后到达稳态所需的电流比补偿前的电流更小,达到稳态的时间更短,转矩突变和转速突变时电流变化与转速波形相对应,符合无刷直流电机运行工况。
图12中4 个关键点的电流仿真波形放大图如图13所示。
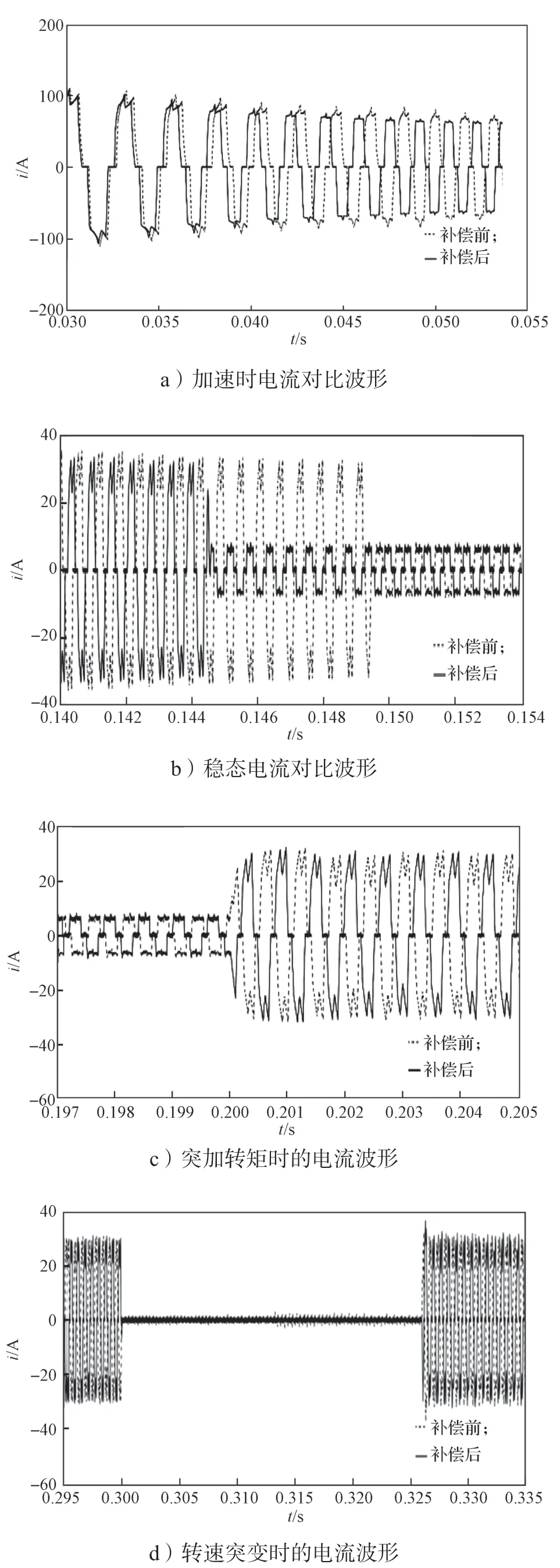
图13 关键点电流仿真波形Fig.13 Key point current simulation waveform
观察图13所示4 个关键点的电流仿真波形放大图,由图a 所示加速时电流波形对比,可以看到经过补偿后加速段所需的电流更小,电流更稳定。由图b可以看出,补偿后电机更快达到稳态。由图c 和图d可以得知,在电机高速状态下转矩突变和转速突变都没有使电机失步,说明在高速状态下系统的抗干扰能力良好。
5 结语
电机实际运行中,当其转速达到1×105r/min时,每一步换相时间为100 μs,但是由于滤波延时、MCU 代码执行时间会导致电机每一步实际换相时间大于100 μs。此时,电机转速将达不到最高运行速度。本研究通过对无刷直流电机控制系统的反电势过零点法的分析,将Simulink 模块中已有模块和S 函数相结合,搭建了高速无位置无刷直流电机控制系统,并且采用速度电流双闭环控制。仿真结果表明,电机运行转速可以达到1×105r/min,引入位置补偿后,电机转速响应更快,所需电流更小,表明补偿算法有效可行,在高速下的转矩突变和转速突变仍可以稳定运行,说明电机的抗干扰能力良好。

