基于扩张状态观测器的反馈线性化无人飞行器姿态控制

姜鸿儒，徐 利，邱令存，李 迪，董诗音

(1.上海机电工程研究所, 上海 201108； 2.上海航天电子技术研究所，上海 201108)

0 引言

无人飞行器由于其可在飞行阶段飞行速度快、性价比高、无人驾驶等特点，因此具有重要的军事意义和民用价值[1-4]。无人飞行器在飞行过程中，由于飞行环境复杂，气动特性变化剧烈，是一个具有不确定性和干扰的复杂非线性系统。因此，设计一个合适的姿态控制器是非常必要的。同时随着任务难度的增加和要求精度的提高，对无人飞行器飞行阶段的姿态控制的要求也越来越高。传统的PID控制方法首先被提出，但其控制精度满足不了当前任务的要求。在此基础上，采用分数阶PID方法来提高飞行器姿态控制性能[5]。文献[6]中，反步法的思想被运用到模型的解耦上，并设计了鲁棒控制器对飞行器姿态进行控制，但文中对干扰的分析较少。文献[7] 中，张教授利用滑模干扰观测器对干扰进行了估计和补偿，并提出了用于飞行器速度和高度跟踪控制的二阶终端滑动控制(2tscm)方法，但文章中也没有考虑干扰的影响。文献[8]中，秦教授在姿态控制方面采用了增益调度方法，但该方法的控制精度有待提高。除此之外，文献[9]采用了基于径向基函数神经网络(RBFNN)的多模型最优控制方法控制飞行器的姿态和文献[10]在滑模控制中加入分数阶微积分增强控制鲁棒性和提高响应特性，但这些方法计算量大，对飞行器的快速响应有一定影响。可见，上述论文存在两个较为普遍的问题。首先，在实际作战中飞行中的飞行器需要一个简单实用的姿态控制器，但以往的姿态控制器参数多，控制复杂，对后期调试和实际验证带来困难。本文将反馈线性化技术[11-12]与反步法技术[9,13-14]相结合，将非线性耦合系统解耦为近似线性系统，使姿态控制器的设计过程系统化、结构化和简单化。其次，由于抑制干扰会产生大量能耗，所以不是解决干扰问题的最佳选择。因此，会采用一些观测器来估计扰动并补偿干扰，如扰动观测器(DOB)[15]、高阶干扰观测器(HODO)[16]、比例积分观测器(PIO)[17]等。除此之外，还有扩张状态观测器(ESO)[16,18-19]，本文将采用ESO方法对干扰进行精确估计和补偿。

本文的贡献在于设计了一种简单实用的控制无人飞行器按照预定期望姿态进行跟踪的姿态控制方法。该方法设计了一种扩张状态观测器来估计和补偿外部和内部扰动。在此基础上，提出了一种基于观测器的高分辨率飞行器姿态跟踪反馈线性化控制器。此外，还证明了闭环系统的稳定性和ESO的收敛性，进一步佐证该方法的可行性和有效性。

本文接下来将从以下几方面介绍：第1节将介绍飞行器的动力学系统及其简化形式，并将动力学系统分为姿态子系统和角速度子系统；第2节将设计扩张状态观测器和反馈线性化控制器；第3节将证明系统的稳定性及观测器的收敛性；第4节将展示仿真结果和讨论；最后，在第6节中给出了结论。

1 无人飞行器运动学模型

我们采用通用的无人飞行器的姿态动力学和运动学模型[21]，如下所示：

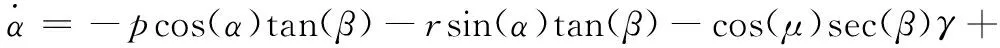
q+sin(μ)sec(β)(χcos(γ)-δsin(χ))+

sin(μ)sec(β)(τ+ΩE)cos(δ)cos(χ)sin(γ)-

sin(μ)sec(β)(τ+ΩE)sin(δ)cos(γ)+

cos(μ)sec(β)[δcos(χ)+(τ+ΩE)cos(δ)sin(χ)]

sin(μ)(τ+δcos(χ))-cos(μ)δsin(χ)sin(γ)+

cos(μ)χcos(γ)+cos(μ)sin(δ)cos(γ)(τ+ΩE)-

cos(μ)(τ+ΩE)cos(δ)cos(χ)sin(γ)

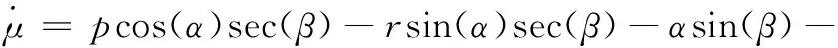
δsin(χ)sec(γ)(τ+ΩE)cos(δ)cos(χ)sin(γ)-

χsin(γ)+(τ+ΩE)cos(δ)cos(χ)cos(γ)

(1)

和:

(2)

其中：x和y表示无人飞行器的航向角和航迹角。δ,τ,ΩE分别表示纬度、经度和地球的角速度。α,β,μ分别表示攻角、侧滑角和倾斜角。p,q,r表示飞行器的体坐标系。Mx,My,Mz表示攻角，侧滑，倾斜角的气动力矩。f1,f2,f3表示额外干扰。Ixx,Iyy,Izz分别表示机体围绕X,Y,Z轴的转动惯量。

为了从状态过程中分离控制器，以及设置有空气动力学参数的不确定性和其他因素所造成的扰动。从模型中可以看出，与姿态角速度相比，姿态角的变化比较缓慢，往往两者间会差几个数量级，由此可以将姿态角速度和姿态角度两者剥离开来，对两者分别进行控制，因此式(1)和(2)通常可以简化为:

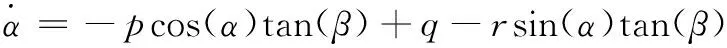
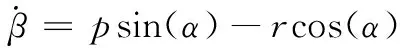
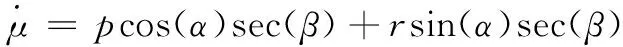
(3)

其中:d1,d2,d3分别为X,Y,Z三轴方向内外扰动之和。

如上所述，相较于姿态角的变化，在飞行的过程中姿态角速度变化更快。当状态变量被时间尺度分离时，动力学系统可以分为两个子系统。一个子系统是状态变量为Ω的角度子系统，另一个子系统是状态变量为的角速度子系统。

定义:

(4)

因此，式(3)可写为如下方程：

(5)

其中：

2 控制器和观测器设计

本节研究的主要目的是实现无人飞行器的姿态高精确控制。利用反步法技术，提出了无人飞行器姿态控制的反馈线性化方法。同时，采用扩张状态观测器对扰动进行精确估计和补偿。

在利用扩张状态观测器消除干扰的影响的基础上，采用反步法通过递归地构造闭环系统的李雅普诺夫函数从而得到反馈控制器，并根据反馈线性化方法将模型和控制器线性化，从而减少调节参数和调节难度。接下来，将采用反步法技术将无人飞行器模型拆分为角速度子系统和角度子系统。

步骤1：

设计虚拟控制变量ω使姿态子系统的跟踪误差收敛到零，从而可以作为角速度子系统的角速度控制输入。

首先，定义:

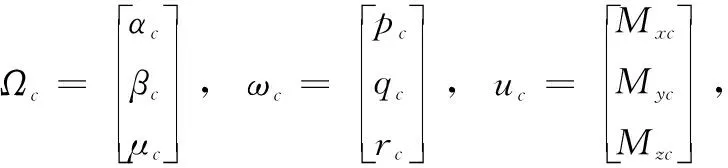
其中：Ωc,ωc,uc分别是子系统和控制扭矩的3个方向控制输入。

可以看出Ω需要跟踪上Ωc才能完成预期角度的跟踪控制，因此建立了姿态子系统的李雅普诺夫函数：

(6)

其中：k=diag(kα,kβ,kμ),kα,kβ,kμ都是正常数，用于调节姿态子系统的误差，以此来让系统为渐近稳定。由于det(F1)=-secβ≠0,F1是可逆的，所以控制器可用。令eΩ=Ωc-Ω)，所以闭环动态系统可写为：

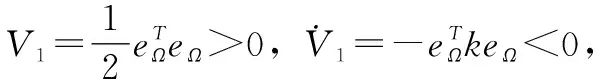
所以可得到角速度子系统的方程是:

接下来将讨论无人飞行器模型中角速度子系统。

步骤2:

在设计角速度子系统控制器之前，需要先设计扩张状态观测器来估计角速度子系统中由复杂环境而引起的不确定性干扰。与其他观测器如干扰观测器、滑模观测器等相比，扩张状态观测器能在不考虑飞行器模型的基础上估计干扰，由于本文采用通用的无人飞行器模型，对部分模型细节并未考虑，因此使用扩张状态观测器更适合此种环境，可以避免因建模不准确而带来的控制误差大的影响，同时可以提高该方法的通用性。因此本文采用了该方法。

根据式(5)，角速度子系统的状态方程可以定义:

因此，可设计扩张状态观测器为:

(8)

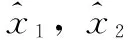
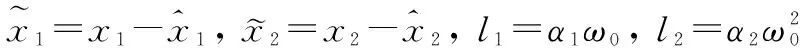
(9)

后面会对该式进行讨论来分析扩张状态观测器的收敛性。

步骤3:

接下来设计实际控制变量u使角速度跟踪误差收敛到小范围内。从式(5)可以看出，角速度子系统是非线性系统，而反馈线性化控制可以对系统进行线性化，从而简化调节参数实现对角速度子系统的高精度控制。反馈线性化控制的控制律设计为:

u=G-1(v-F2(ω))

(10)

其中：v是控制输入，然后将反馈控制量u引入非线性系统，得到线性化的一阶微分线性系统：

(11)

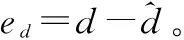
可以看出，通过反馈线性化，原非线性系统可以线性化为线性系统，因此线性系统可以采用线性控制方法设计控制器来控制v变量:

其中：kf=diag{k1,k2,k3},e=ωc-ω。

根据上述公式，我们可以得到实际控制变量u如下：

(12)

3 稳定性分析

在设计完角度子系统和角速度子系统的两个控制器后，本节将分为以下两个步骤进行介绍：1)证明设计的扩张状态观测器能使内部外部扰动的估计误差收敛到小范围；2)证明在干扰的条件下具有反馈线性化和ESO的闭环系统(角度子系统和角速度子系统)是稳定的。通过证明扩张状态观测在干扰条件下收敛性为角速度子系统稳定控制提供基础，得到实际的角速度可以跟踪到预期的角速度值，再通过设计李雅普诺夫函数来证明角度子系统的稳定，从而完成整个无人飞行器姿态控制的稳定性分析。

3.1 扩张状态观测器收敛性分析

本小节主要来证明在内外干扰影响的条件下通过扩张状态观测器可预估干扰值，并将干扰补偿到一个误差范围内。现给出定理1，如下

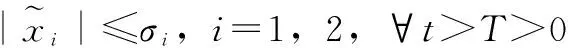
证明

定义:

(13)

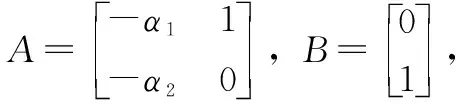
根据式(13)，ε可表示为:

(14)

令

其中:

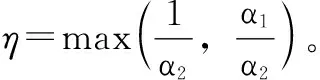
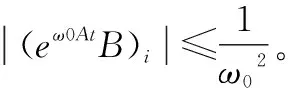
令:

可得，

|(A-1eω0AtB)i|=|si,1d12+si,2d22|≤

(15)

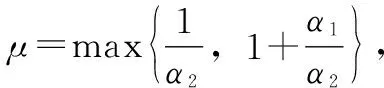
(16)

令:

εsum=|ε1(0)|+|ε2(0)|

(17)

可得，

(18)

3.2 闭环系统稳定性分析

定理2:考虑角速度子系统(7)，如果实际控制变量u设计为(12)，则闭环系统是稳定的。

证明

设计李雅普诺夫函数为:

可以计算V2的导数，为:

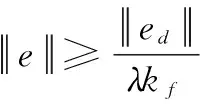
根据上述结论和式(7)，进一步证明角度子系统的稳定性，可得如下，

(F1(Ω)e-keΩ)TeΩ≤

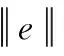
至此，扩张状态观测器的收敛性、角速度子系统和角度子系统的稳定都已证明完成，从而可得闭环无人飞行器系统稳定。

4 仿真结果与分析

本节将给出了一些根据所设计的控制器做出的仿真结果，以证明本文所提供的理论方法的可行性和有效性。首先，以无人飞行器的攻角为例，给出了所设计的扩张状态观测器的仿真结果。根据飞行器的动力学系统模型(3)，我们假设系统在没有控制输入的情况下，只在系统中加入干扰源以此来判断所设计的扩张状态观测器是否能准确对干扰进行估计。在图1中，干扰源(绿线)是余弦信号，扩张状态观测器的初始状态假定都为零。其中将扩张状态观测器的参数设置为α1=2,α2=1,ω0=67,G=8.9。从仿真结果中可以看出，扩张状态观测器可以很好地对干扰进行跟踪(红线和绿线几乎重合)。在仿真运行到0.3 s处，期望角度由0°转为余弦值，实际的跟踪结果会有0.1～0.3°左右的波动，后续快速响应跟上期望的余弦值角度，随后的整个跟踪过程的角度误差都在期望角度值的1%以内，是符合实际的工程需求的。可以得出所设计的扩张状态观测器能快速且高精度对干扰源进行估计。

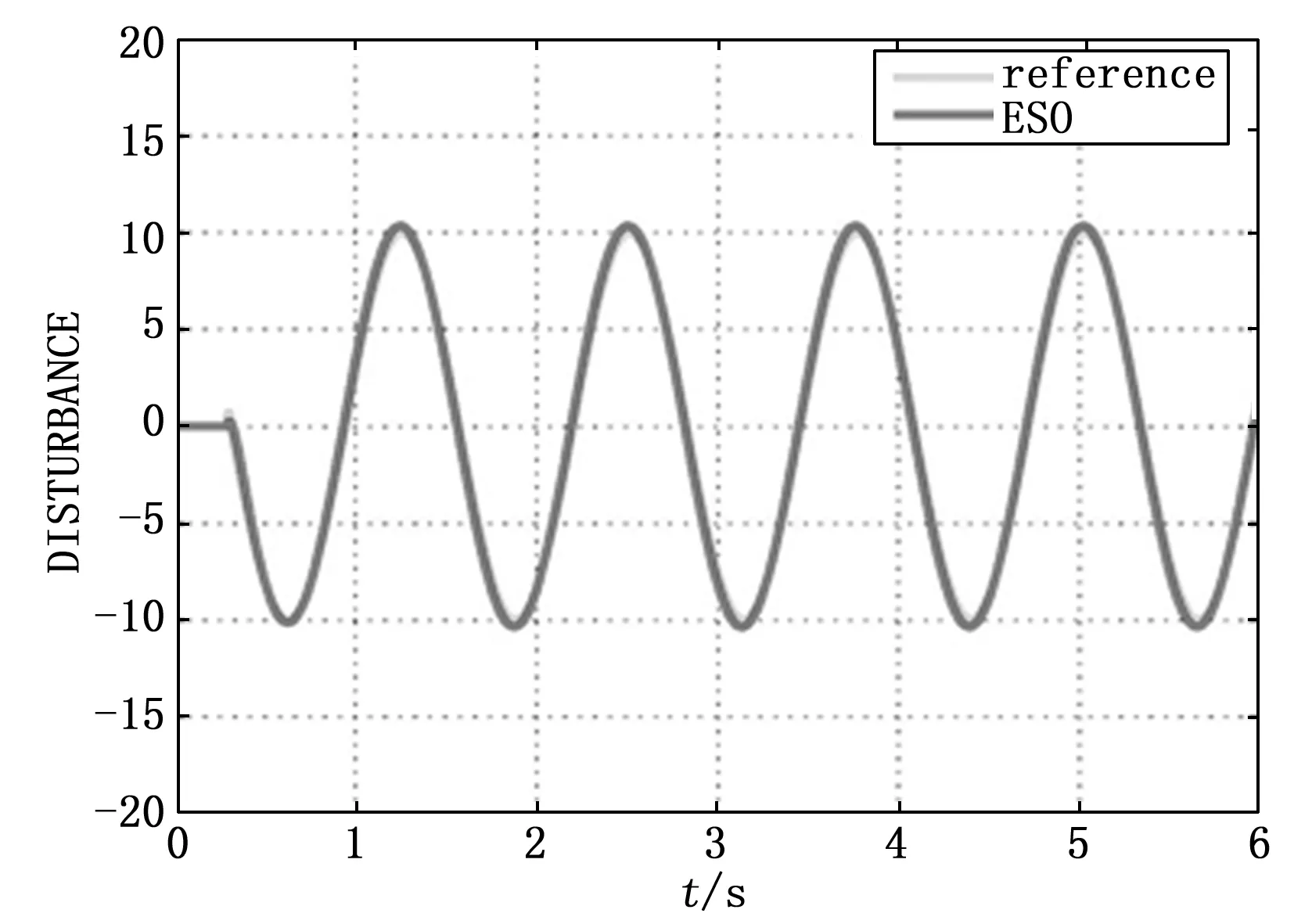
图1 扩张状态观测器估计干扰

在验证了扩张状态观测器的预估补偿效果后，开始对基于扩张状态观测器的反馈线性化方法的姿态控制方法进行检验。我们假设无人飞行器的攻角、侧滑角、倾斜角及其3个方向的角加速度的初始状态都为零，攻角、侧滑角、倾斜角的期望值设定为[10°,0°,-5°]。与此同时，我们分别在角速度子系统的3个方向中加入一定的干扰，为了更符合实际的环境下干扰噪声，我们将干扰设定为[cos(0.01t),0,0.5*sin(0.05t)]。此时，kf的参数值为diag{8.928,0.16,9.209}和k的参数值为diag{4.45,0.12,1.92}。仿真结果如下。

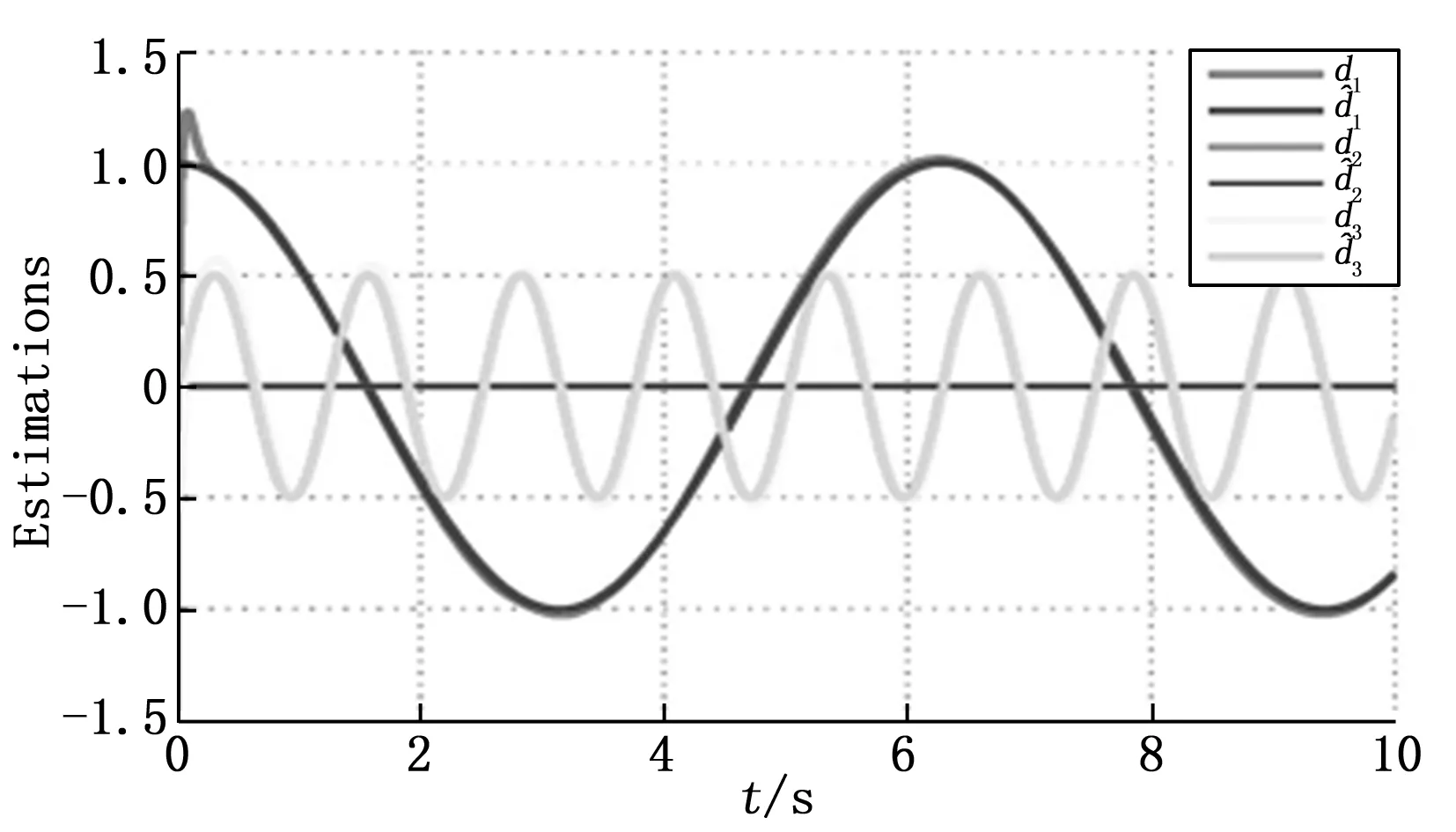
图2 加入扰动的姿态控制

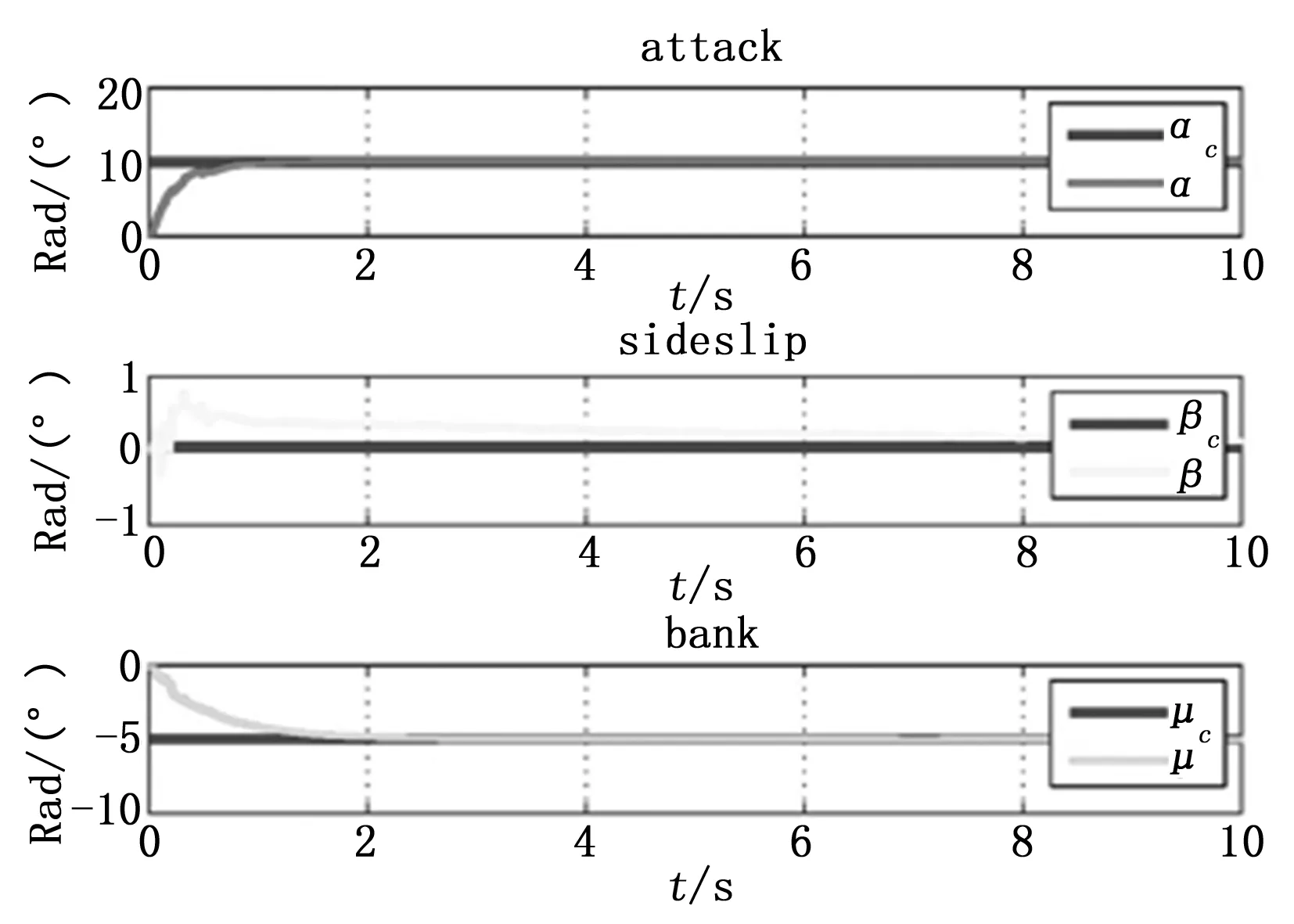
图3 基于扩张状态观测器的反馈线性化姿态控制

从图2可以看出，在整个无人飞行器姿态控制的过程中，扩张状态观测器可以从初始状态快速响应跟踪到预期的角度值上，同时可以很好地对攻角、侧滑角、倾斜角这3个方向的干扰进行预估，角度误差都在0.01°的数量级内浮动，符合之前的验证结果。从图3可以看出，通过基于扩张状态观测器反馈线性化姿态控制方法对攻角、侧滑角、倾斜角3个方向的角度跟踪都有着不错的表现，可以快速响应从初始状态跟踪到预期的角度值上，同时，在[cos(0.01t),0,0.5*sin(0.05t)]的干扰下，可以看出利用扩状态观测器可以很好地对由无人飞行器产生的干扰进行估计并补偿。所以，从图2、图3的仿真结果可以看出，该方法可以很好地解决无人飞行器在干扰条件下的姿态控制问题。

5 结束语

针对无人飞行器飞行过程中的时变姿态跟踪问题，本文设计了一种基于反步法技术的反馈线性化控制方案来控制飞行器的姿态。同时，采用扩张状态观测器对模型的扰动进行估计和补偿。给出扩张状态观测器的收敛性和闭环无人飞行系统的稳定性证明该理论方法的可行性。同时对该方法进行了相应的仿真，仿真结果证明了控制算法的有效性和干扰估计的准确性，显示了快速准确的姿态控制性能。