基于卡尔曼滤波器的分数阶PIλDμ控制器

蔡元宵 王芸芳

(1.宁夏大学新华学院信息与计算机科学系,宁夏银川 750021;2.陕西汽车控股集团有限公司技术中心,陕西西安 710200)

0 引言

Podlubny在文献[1]中提出了分数阶PIλDμ控制器,其比整数阶控制器多了两个可调参数:积分阶次λ和微分阶次μ,参数调整范围增大,能够更灵活地控制系统。文献[2]提出了用主导极点法设计分数阶PIλDμ控制器。文献[3]采用幅值裕量法和相位裕量法得出了分数阶PIλDμ控制器的参数。针对非线性、参数时变及大范围摄动系统,结合智能优化算法,文献[4]提出了用遗传算法对分数阶PIλDμ控制器的参数进行整定。文献[5]将粒子群优化算法用于分数阶PIλDμ控制器的设计。文献[6]给出了分数阶PIλDμ控制器的数字实现方法,为其工程应用提供了可能性。文献[7]利用控制系统在满足相位裕度和幅值裕度的鲁棒性条件下,设计了对时间常数变化具有鲁棒性的分数阶PIλDμ控制器。然而,实际系统中的过程噪声和测量噪声往往使控制器不能达到理想的控制效果,上述分数阶PIλDμ控制器的设计和研究尚未考虑这些干扰噪声的影响。

卡尔曼滤波器具有递归、线性、无偏和方差最小等特点,因此在对机动目标的跟踪中具有良好的性能,例如在军事、航天和工业生产的自动控制领域都有广泛的应用。文献[8]将模糊控制器的设计与卡尔曼滤波算法融合,提出了一种新的模糊卡尔曼滤波器,在实时性要求很高的控制系统中具有良好的控制性能。文献[9]将卡尔曼滤波器用于视频监控系统,对运动目标的适时检测和跟踪具有良好的效果。

本文将分数阶控制理论和卡尔曼滤波算法进行结合,考虑实际系统中干扰噪声的影响,设计出基于卡尔曼滤波器的分数阶PIλDμ控制器,使系统具有较好的控制性能,且能有效地滤除噪声。

1 分数阶微积分及卡尔曼滤波原理

分数阶微积分是指微积分的阶次是任意的,分数阶微积分常用Grunwald-Letnikov(G-L)定义和Riemann-Liouville(R-L)定义。本文所采用的是G-L定义,即:

设f（t）在区间[a,t]有m+1阶导数,α为任意实数,则α阶次的微分定义为:

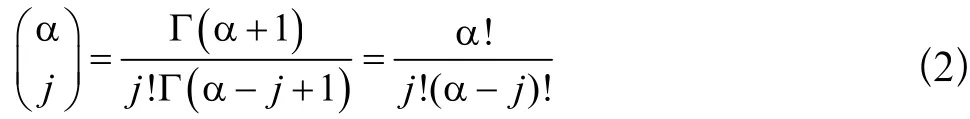
设离散控制系统的状态方程为:

系统的观测方程为:

设控制系统的输出Z(k+1)为实际可测量,卡尔曼滤波递推算法如下:

设现在系统的状态是k,可根据系统k时刻状态预测k+1状态,即状态的预测方程为:

状态更新后,可进一步更新协方差,即协方差的一步预测方程为:

图1 基于卡尔曼滤波器的分数阶PIλDμ控制器的控制原理图Fig.1 Control schematic of the fractional order PIλDμ controller based on the Kalman filter

滤波增益方程为:

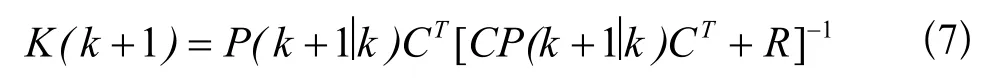
滤波估计方程为:

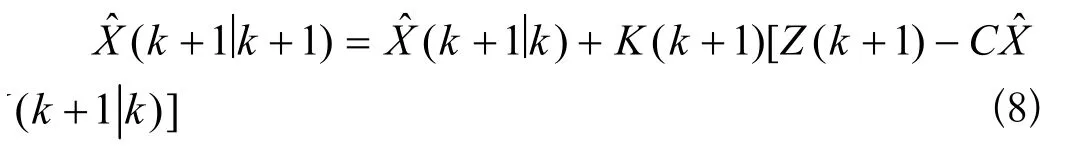
滤波协方差更新方程为:

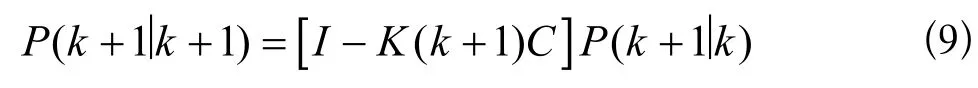
2 基于卡尔曼滤波器的分数阶PIλDμ控制器

基于卡尔曼滤波器的分数阶PIλDμ控制原理如图1所示,其中将连续的被控对象通过零阶保持器进行离散,并考虑测量中产生的干扰噪声v。经过数字分数阶PIλDμ控制器的输出记为u,将其作为被控对象的输入。

设图中的连续被控对象为单输入单输出系统,其传递函数为:

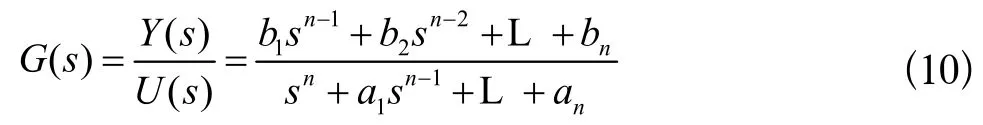
将(10)式转化为连续系统的状态方程为:

其中:

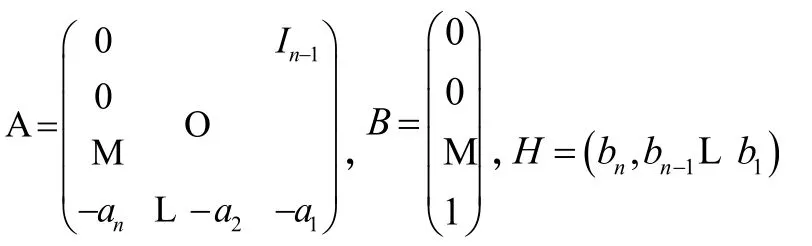
使用零阶保持器,建立离散系统状态空间模型为:

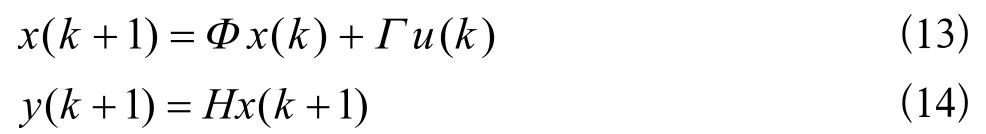
在考虑干扰噪声时,由(13)和(14)式可得:

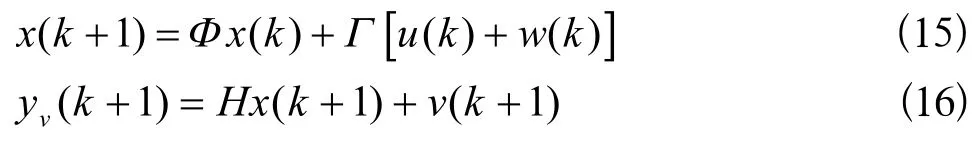
其中:w(k)为控制干扰噪声,v(k)为测量干扰噪声。

分数阶PIλDμ控制器的时域方程为:

式中:λ和μ分别为分数阶PIλDμ控制器的积分阶次和微分阶次。

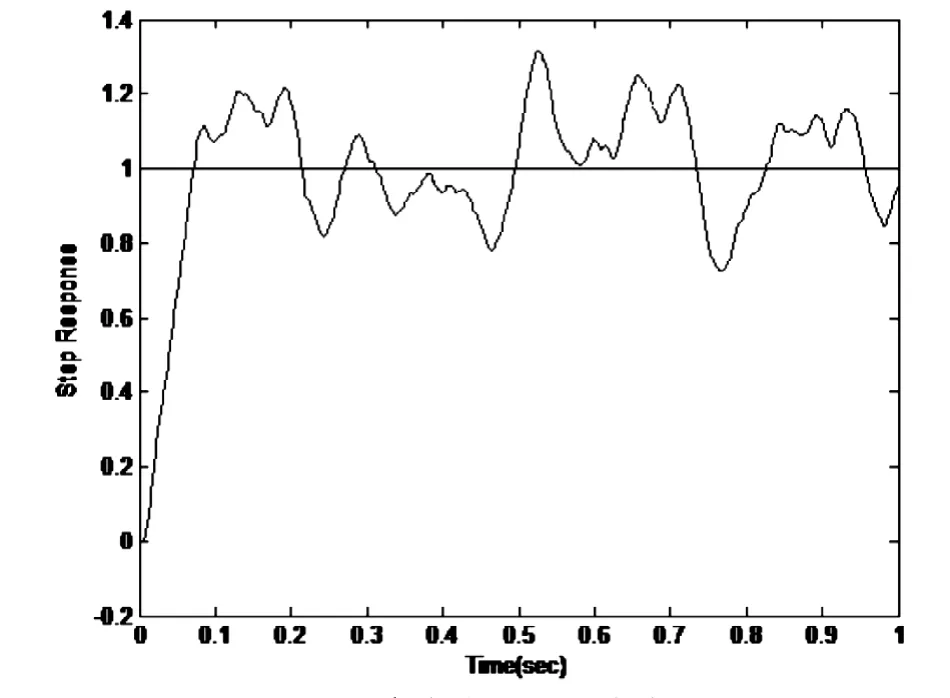
图2 系统的单位阶跃响应图(未加卡尔曼滤波器的整数阶PID控制器作用)Fig.2 The unit step response of the system(integer order PID controller without the Karman filter)

根据α阶次的微分定义,结合“短时记忆法”,得到分数阶微积分的数字形式为:

其中的二项式系数可通过下式来计算:

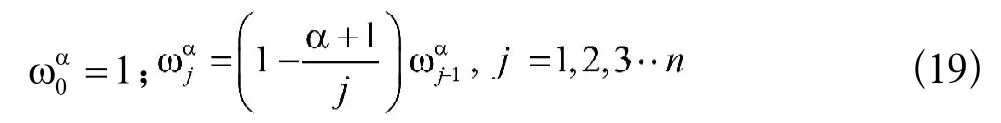
由(17)～(19)式可得,分数阶PIλDμ控制器的数字离散形式为:

其中:偏差e（k） =rin（k） -ye（k）,qj和dj可通过(19)式计算,ye(k)由下式给出:

综上,结合公式(5)～(9),对于(15)和(16)式表出的系统,给出卡尔曼滤波算法如下:

表1 系统加入滤波器后在不同控制器作用下的性能指标Tab.1 The performance indicator of the system under different controller with the filter

图3 系统的单位阶跃响应图(基于卡尔曼滤波器的整数阶PID控制器作用)Fig.3 The unit step response of the system(integer order PID controller based on the Kalman filter)

图4 系统的单位阶跃响应图(未加卡尔曼滤波器的分数阶PIλDμ控制器作用)Fig.4 The unit step response of the system(fractional order PIλDμ controller without the Karman filter)

3 仿真算例

例:设被控系统的传递函数为[4]:

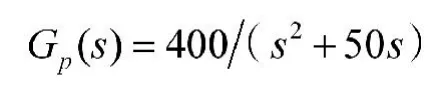
测量干扰噪声信号的幅值为0.003,协方差R为1;控制干扰噪声信号的幅值为0.003,协方差Q为1。

对此被控系统,采用文献[4]中遗传算法设计的整数阶PID控制器和分数阶PIλDμ控制器的传递函数分别为:

图5 系统的单位阶跃响应图(基于卡尔曼滤波器的分数阶PIλDμ控制器作用)Fig.5 The unit step response of the system(fractional order PIλDμ controller based on the Kalman filter)

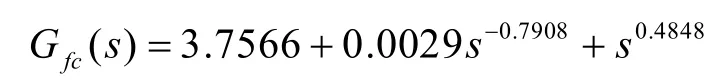
仿真结果见图2-5,从中对比可知,在考虑过程噪声和测量噪声时,若不加卡尔曼滤波器,分数阶PIλDμ控制器和整数阶PID控制器均不能很好地发挥控制作用。反之,在加入卡尔曼滤波器后,控制器既能很好地控制被控对象,使系统具有良好的控制性能,又可有效地滤除干扰噪声。仿真结果表明基于卡尔曼滤波器的分数阶PIλDμ具有很好的控制性能。

系统加入滤波器后在不同控制器作用下的主要时域性能指标见表1,从中分析可知基于卡尔曼滤波器的分数阶PIλDμ比基于卡尔曼滤波器的整数阶PID控制器具有更好的控制性能。

4 结论

通过仿真对比表明:对于相同的被控对象,分数阶PIλDμ控制器具有良好的控制性能,同时在系统存在干扰噪声的情况下,加入卡尔曼滤波器可有效地滤除噪声,使系统具有良好的控制性能。