陶瓷封装的等效热方法及其仿真验证
(中国电子科技集团公司第五十八研究所,江苏无锡 214035)
1 引言
未来电子器件的发展趋势是高集成度、高速度以及小尺寸化,这使得芯片在制造时的晶体管密度也逐渐增加,同时这也导致了芯片产生的热量越来越大,如果不能将多余热量散发出去,芯片的温度就会急剧升高,从而严重影响芯片的性能和可靠性[1]。为了保证高集成度下的芯片能够稳定工作,芯片的散热设计显得尤为重要[2]。
通过模拟仿真的方法,对不同方案的散热设计进行对比分析,可以极大地提高散热设计的效率。傅广操等人[3]利用等效热模型理论对三维堆叠中的TSV 插入层、焊接凸点层等进行了简化,并对整体封装进行了三维结构热仿真,利用精确模型的仿真结果作为参照,证明了TSV 等效热模型的可行性,为快速获取整体结构的温度场分析结果提供了一种可靠方法。
本文使用Icepak 热分析软件[4]对陶瓷封装器件进行了仿真分析。根据JEDEC 标准中JESD51-5,对陶瓷封装器件与测试板的连接进行了规范,即关于设置热沉的陶瓷封装器件可以通过在测试板上设置规定数量的铜柱进行散热。文章对与陶瓷连接的测试板连接及散热区域(Through Board Via,TBV)进行了热模型等效,根据单位厚度内热流量恒定原理,得出了关于测试板连接散热区域的等效热阻的计算公式。
通过T3Ster-热阻测试仪对陶瓷器件热阻进行测试,并将计算得到的热阻值与仿真得到的热阻值进行对比验证,结果表明,通过等效热阻模型得到的仿真值与原模型仿真得到的仿真热阻值及实测的热阻值具有较好的一致性,表明了等效热模型理论的实用性。
2 封装器件模型及材料参数
对陶瓷封装器件与测试板的连接结构进行三维建模。其结构分别由盖板、陶瓷基板、芯片、贴片胶、散热片、铜片、铜柱、引脚及PCB 板组成。因为考虑到仿真计算效率的问题,对模型中的倒角、圆角及键合丝等对热传导影响较小的结构进行了适当简化,得到模型如图1 所示,材料参数如表1 所示。
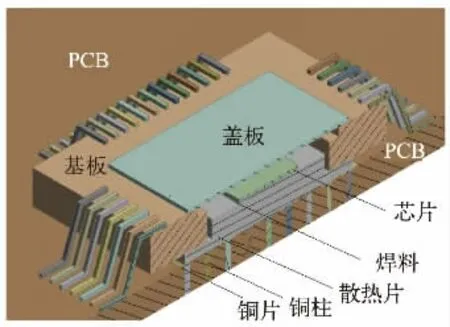
图1 陶瓷封装体与测试板连接结构图

表1 材料参数
3 封装器件热模型等效
3.1 等效模型单元提取
对陶瓷与测试板连接区域(TBV)的热模型进行等效,即将铜片与PCB 等效成一块各向异性的单元块,同时将铜柱与PCB 等效成一块各向异性的单元块。此时,单元块在x-y 向和z 向的热导率呈各向异性。简化需要满足一定的条件:(1)简化前后的尺寸保持不变;(2)等效前后的模型传热效果保持不变,即等效单元块的热导率与实际模型等效热导率相同。如图2(a)所示为等效前的模型侧面视图,图2(b)为等效后的模型侧面视图。
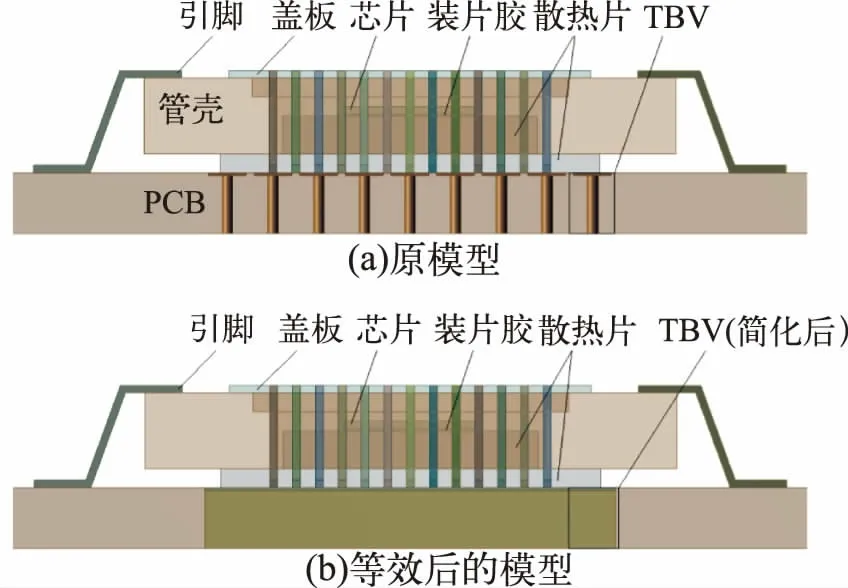
图2 模型侧面视图
对连接的TBV 区域展开为平面图,如图3 所示,将需要阵列等效的区域分为两块,一块为由PCB 环绕的铜片阵列,另一块为由PCB 环绕的铜柱阵列,分别提取其单元如图3(a)、(b)所示。
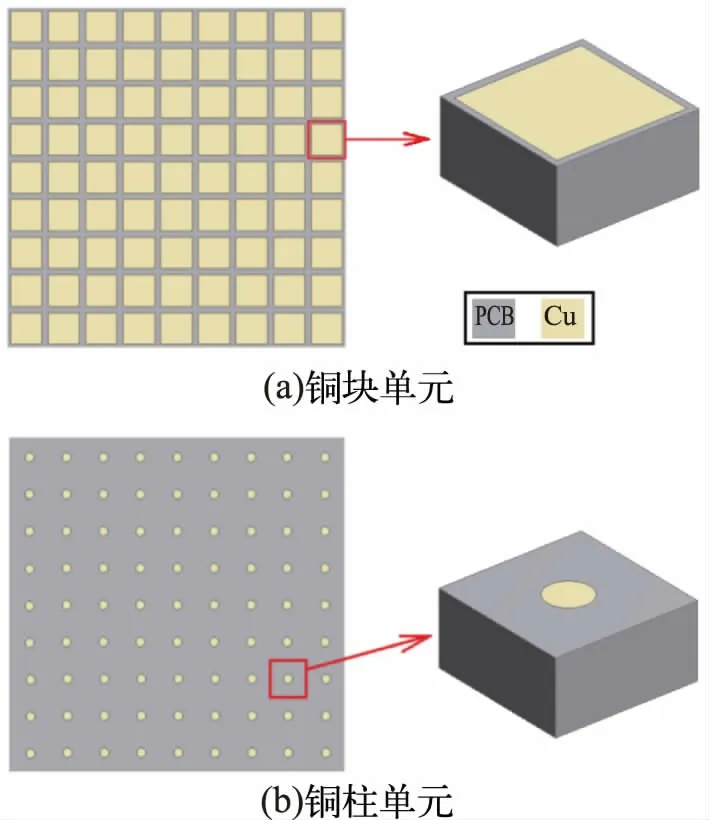
图3 单元块提取图
3.2 等效模型热导率计算
热阻是指热量传递通道上两个参点之间的温度差与热源功率之间的比值[5],如式(1)所示:

其中,R 为两点间的热阻(单位℃/W 或K/W),△t 为两点间的温度差(单位℃),P 为两点间的热源功率(单位W)。
导热基本公式为:

其中,L 为热传导距离(单位m),S 为热传导截面积(单位m2),K 为热导率(单位W/m℃)。根据式(1)和式(2),得到热传导模型的热阻计算公式:

由式(3)可知,热传导距离越短、截面积越大以及材料的热导率越高,两点之间的热阻值越低。因此,在封装设计中采用合理的结构和选用合适的材料,对减小封装器件的热阻起到了至关重要的作用。
通过对式(3)进行变换,得到式(4):

根据单元块的对称性,取1/2 模型单元作为分析对象。如图4(a)所示是PCB 环绕铜柱阵列单元块,图4(b)为焊柱简化后的单元块,其中a 为单元块的长度,r为焊柱的半径。
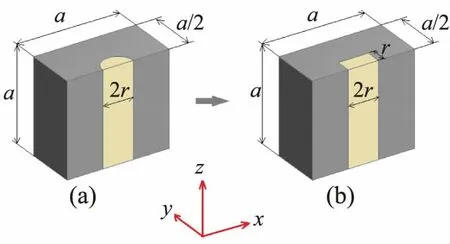
图4 PCB 环绕铜柱阵列单元块
先计算PCB 环绕铜柱阵列单元块的热阻。在z 方向,其单位长度等效热阻有如下关系式[3]:
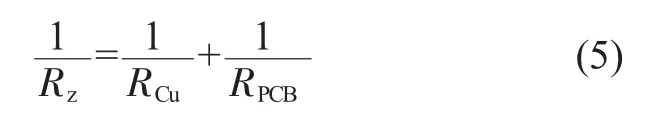
其中RCu、RPCB为单位长度的热阻。
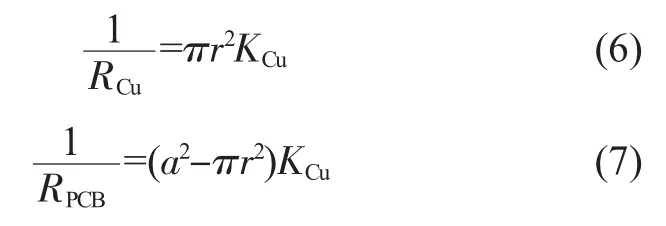
其中KCu、KPCB分别为铜的热导率和PCB 的热导率。
根据式(4)可知,单位长度上的z 方向等效热导率为:
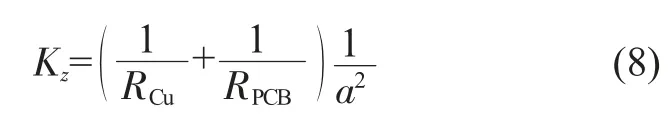
令α=2r/a,结合式(6)、(7)、(8)得到式(9):
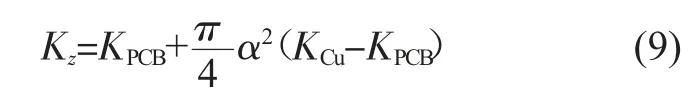
对于x、y 方向,采用相同的方法可以得到其单位长度等效热阻为:
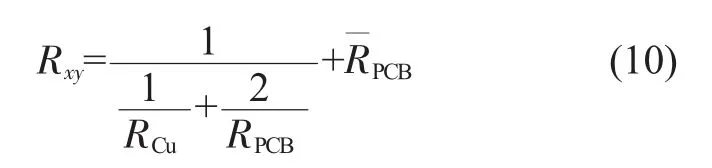
结合式(4)、(10)可得,单位长度上x、y 方向上的等效热导率为:
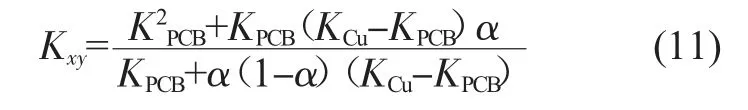
代入数据a=1.2 mm,r=0.15 mm,得到PCB 环绕铜柱阵列单元块的等效热导率Kxy=35.73,Kz=217.14。
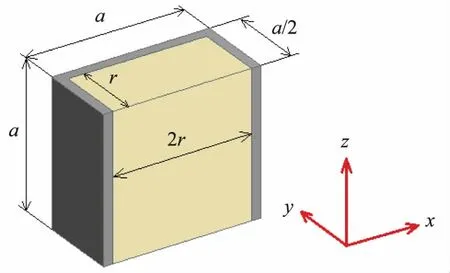
图5 PCB 环绕铜片阵列单元块
PCB 环绕铜片阵列单元块如图5 所示,使用上述相同的计算式,带入数据a=1.2 mm,r=0.5 mm,可得其等效热导率Kxy=24.82,Kz=19.89。
4 封装器件结环境热阻仿真
通过Icepak 热分析软件分别对原模型及等效后的模型进行自然对流下的结环境热仿真,设置芯片发热功耗为2.4 W,环境温度为25 ℃,仿真得到等效模型和原模型的芯片结温分别为53.81 ℃、51.37 ℃,其温度分布的云图分别如图6、图7 所示。通过式(1)计算得到原模型和等效模型结到环境的热阻分别为11℃/W、12 ℃/W,整理得到结环境热阻的条件及结果如表2 所示。

表2 结-环境热阻仿真结果
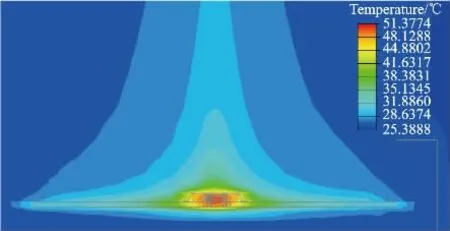
图6 结环境热仿真温度分布云图(原模型)
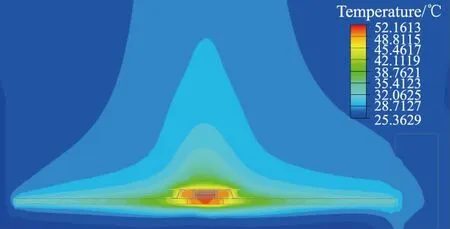
图7 结环境热仿真温度分布云图(等效模型)
5 热仿真及结果对比验证
根据JEDEC 标准中JESD51-1、JESD51-2 热阻测试方法,将焊接在PCB 板上的封装器件放置在静止空气测试箱中进行测试,同时使用热电偶探测得到静止空气测试箱中的环境温度,根据热阻计算公式θja=(tjta)/P 计算出封装器件结-环境热阻θja。
测试中采用1 A 加热电流,1 mA 测试电流。取3个样品通过热阻测试设备进行测试,得到封装器件测试的平均结温如表3 所示,热阻测试结构曲线如图8所示。通过计算,得到实际工况下封装器件的结-环境热阻(θja)测试结果为10.86 ℃/W。

表3 结-环境热阻测试结果
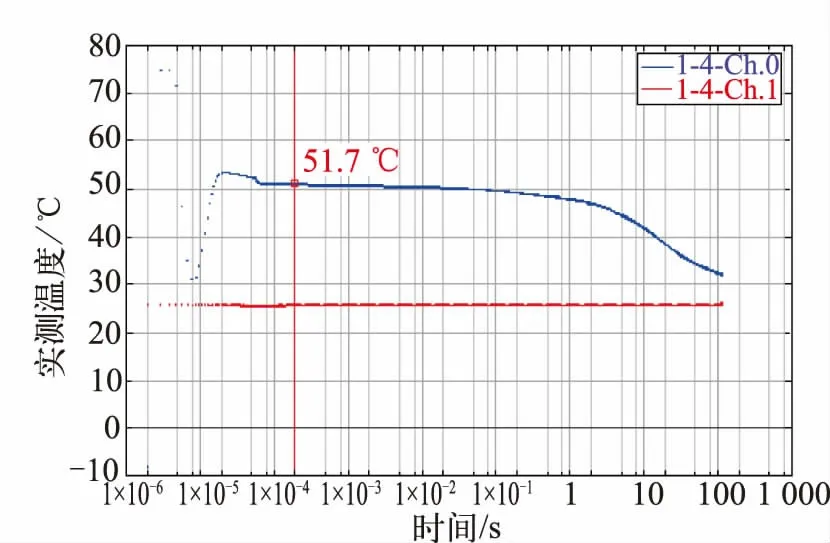
图8 封装器件热阻测试温度曲线图
通过实测及计算得到陶封器件的结环境热阻值为10.86 ℃/W,仿真计算得到陶封器件在等效热模型下的结环境热阻值为11.32 ℃/W,原模型的结环境热阻为11 ℃/W。等效热模型下的结环境热阻值是实际热阻值的4.2%,原模型的热阻值是实际热阻值的1.3%,其热阻值与实测值对比的偏差均在5%以内,因此通过等效热模型的方法可以获得精度较高的陶瓷封装器件的结环境热阻值[6]。
6 结论
本文利用等效热模型理论,对用于陶瓷封装器件测试的PCB 及其铜柱的热阻进行了等效计算,通过对等效热模型与原模型进行结环境的热仿真,得到了等效热模型的热阻值与原模型热阻值,与实际热测试的阻值对比有良好的一致性,其偏差均在5%以内,表明了所采用的等效热模型仿真计算方法的可行性,为陶瓷封装器件在PCB 等复杂模型中的组合热仿真计算提供了一种简单可行的方法。

