孤岛微电网中基于电压-频率下垂与磁链-相角下垂两种控制策略的性能比较

（国网浙江省电力有限公司培训中心，杭州 310015）

0 引言

根据2019 年《BP 世界能源统计年鉴》，煤、石油、天然气等传统化石能源需求仍在持续增长，碳排放增速也达到了近7 年以来的最高水平[1]。考虑到化石能源的不可再生性及高碳排放的危害，推行清洁能源发电方式十分重要。基于太阳能、风能等清洁能源的DG（分布式电源）具有控制灵活、低碳排放等一系列的优点。但是，由于太阳能、风能等自然界能源能量密度波动大、发电时间不连续，控制难度大等特点，大量以该类能源为载体的DG 并入传统电网会给系统的安全稳定运行带来极大的挑战。同时，IEEE P1547规定：当电力系统出现故障时，DG 必须立即脱离主网。这极大地限制了DG 作用的发挥[2]。

为了解决DG 直接接入带来的系列问题，充分发挥DG 的作用，引入了微电网技术[3-6]。微电网通过先进的电力电子技术，有效整合了DG、储能、负荷、控制保护系统等，为传统电网供电提供了有力的补充和支持[7]。微电网通过静态开关与主网相连。当静态开关闭合时，微电网处于并网状态，由大电网提供频率和电压的支撑。当静态开关断开时，微电网处于孤岛状态，此时需要微电网自身建立系统内的电压和频率平衡[8]。

孤岛状态下，微电网作为一个独立的主体运行，要在系统内建立起稳定的电压，需要对逆变器采取有效的控制措施。下垂控制就是其中最常用到的一种控制方法，它具有独特的控制优点：一方面，控制信息来源于本地，不需要额外增加通信设备进行远端信息传输；另一方面，当微电网内有DG 投入或退出时，其它DG 的控制不受影响，无需对其控制系统进行二次调整，系统扩容方便，可以实现微源的“即插即用”[9]。

通过对相关文献进行总结，下垂控制可以分为两大类：一类是基于电压的下垂控制方法，另一类是基于磁链的下垂控制方法[10]。在电压下垂控制中，通过对电压、频率两个参数进行控制，建立起系统内的电压平衡。控制系统中存在多重反馈环路，需要整定电压外环的PI 参数和电流内环的P 参数[11]，三个参数的整定过程比较复杂，需要耗费大量的时间。另外，根据下垂关系，当DG 输出功率不等于额定功率时，电压和频率会相应地偏离额定值，电压偏差和波动会造成电能质量下降，无法满足负荷的用电需求。磁链下垂控制采用一种新的思路，根据电压与磁链间的积分关系，将电压下垂转换为磁链下垂，通过间接地对磁链和相角两个参数进行控制，建立起稳定的系统电压。在控制方法中，用DFC（直接磁链控制）取代了多环反馈控制，避免了复杂的参数整定，控制过程简单。控制中还有一个显著的优点：利用相角下垂代替频率下垂，避免了有功偏差直接带来的频率偏差，频率偏差大大减小[10]。

为了更深入地了解以上两种下垂控制方法，方便以后在微电网系统中的推广应用，本文对上述两种方法进行了比较。首先，分析了两种控制方法的原理。接下来，设计了两种方法的控制方案。最后，基于MATLAB 仿真平台对同一个算例下两种控制方法的控制性能进行了比较。

1 下垂控制原理

1.1 电压下垂控制原理

DG 以逆变器为接口接入电网，图1 为DG的等效接入电路。

图1 DG 的等效接入电路

传统的电压下垂控制公式为[12]：

式中：ω，V 分别代表角频率和电压幅值；ωn，Vn为其对应的额定值；m，n 分别为有功-频率和无功-电压下垂系数；P，Q 分别为输入到负载侧的有功功率和无功功率；Pn，Qn为额定的有功和无功功率。

1.2 磁链-相角下垂控制原理

电压和磁链满足积分关系，经推导可以得到磁链下垂控制公式[10]：

2 下垂控制器设计

2.1 电压下垂控制原理

电压下垂控制结构如图2 所示，主要有功率控制模块，电压-电流双环控制模块和SPWM（正弦脉宽调制）模块等。控制原理如下：将负载电压和电流送入功率控制模块，经过平均功率计算、下垂控制、电压合成等环节得到三相参考电压值，接下来经过电压外环和电流内环得到调制信号，最后通过SPWM 产生逆变器驱动信号，从而建立稳定的系统电压。

2.1.1 功率控制模块

在d-q 坐标系下，负载侧的瞬时功率p 和q可以表示为：

图2 电压下垂控制结构

通过一阶低通滤波器可以得到平均功率P 和Q。已知平均功率，结合电压下垂公式，可以得到参考电压幅值E*和ω*参考角频率，由此得到三相参考电压。

2.1.2 电压电流双环控制模块

本文采用了电容电流内环、电感电压外环控制策略。电压外环采用PI 参数调节以保证对负载电压的准确跟踪，电流内环采用P 参数调节以提高动态响应速度。在双环控制中，选择合适的PI和P 参数十分重要。三个控制参数的选取需要复杂的参数整定。

2.2 磁链下垂控制器设计

磁链下垂的控制结构如图3 所示，主要由功率控制器和DFC（直接磁链控制器）组成。首先，利用负载电压e 和电流i 计算得到平均功率，再结合磁链下垂公式得到参考磁链幅值和相角δref。在直接磁链控制器中，将两个参考值与实测值进行比较，得到偏差符号，再结合磁链矢量的具体位置，通过矢量选择表进行矢量选择，从而实现对磁链幅值和相角的跟踪控制。控制中用两个滞环比较器取代了PI 调节，省去了复杂的参数调试过程，控制难度大为减小。控制过程中，磁链幅值和相角的跟踪精度取决于滞环宽度。

2.2.1 功率控制器

磁链下垂控制在α-β 坐标系中进行。此时瞬时有功功率p 和瞬时无功功率q 的表达式为：

图3 磁链下垂的控制结构

式中：eα和eβ为负载侧电压在α-β 坐标系中的电压分量；iα和iβ为负载侧电流在α-β 坐标系中的电流分量。通过低通滤波器得到平均功率P 和Q，将计算得到的功率送入磁链下垂控制公式，即可得到和δref。

2.2.2 直接磁链控制器

图4 DFC 的控制结构

在DFC 中，磁链幅值和相角的计算公式为：

式中：ψVα和ψVβ为逆变器侧磁链的α 轴和β 轴分量，满足：

偏差信号定义为：

α-β 平面的6 扇区划分如图5 所示，整个平面被划分成6 部分，每部分60°，按逆时针方向依次命名为S1—S6。其中，S1扇区以水平轴线α为对称轴，上下角度各15°。V0—V7代表了8 种不同的开关状态，V1—V6是6 个工作电压矢量，V0和V7是两个零开关矢量。需要注意的是：V1—V6的作用效果均使相角增大，只有V0和V7两个零开关矢量才能减小相角值[13]。

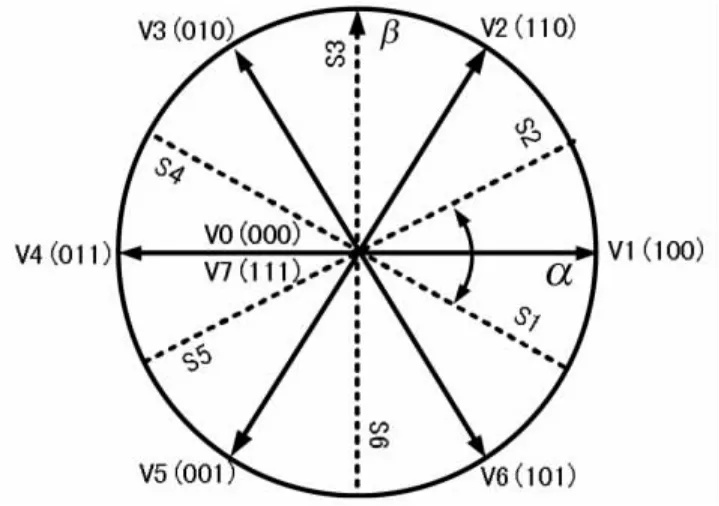
图5 平面的6 扇区划分

表1 开关矢量选择

在该类下垂控制中，磁链是与电压紧密相关一个控制变量，DFC 减小了控制的难度，但是由此产生的磁链脉振会影响系统输出电能的质量。

3 建模与分析

图6 为仿真微电网模型，其元件参数见表2。S 为负荷投切开关，t=0.15 s 时，S 闭合，负荷增加。

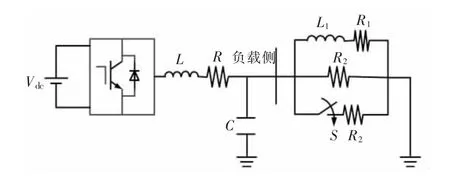
图6 仿真微电网模型

表2 微源参数

3.1 电压下垂控制仿真结果

采用电压下垂控制得到的电压波形如图7 所示。从图7（a）中可以看到，系统电压在很短的时间内（约0.01 s）就能达到稳定值。t=0.15 s 时，R2投入，系统有功负荷增加，无功负荷不变，因此开关闭合前后电压波形无明显变化。对负载变化前后电压进行谐波分析（分别取t=0.1 s、t=0.2 s），可以看到负载变化前总谐波畸变率仅为0.34%，变化后谐波畸变率为0.88%，如图7（b）所示。

图7 电压下垂控制中的输出电流

图8（a）为电压下垂控制中得到的输出电流波形。与电压类似，电流也能在很短的时间内达到稳定值。t=0.15 s 时，有功负荷增加，相应的电流幅值增大。对负载变化前后电流进行谐波分析（分别取t=0.1 s，t=0.2 s），可以看到负载变化前电流总的谐波畸变率仅为0.30%，变化后总谐波畸变率为0.80%，电流波形质量良好。

图8 电压下垂控制中的输出电流

图9 为系统输出的频率波形。由图9 可知：初始时刻系统频率为60.24 Hz，0.15 s 之前频率稳定在59.88 Hz，0.15 s 之后频率稳定在59.71 Hz，分别偏离额定频率值+0.24 Hz，-0.12 Hz，-0.29 Hz。当输出有功不等于额定值时，系统频率会相应地偏离额定值，甚至出现频率越限，这是传统电压下垂中的一个显著缺陷。

图9 电压下垂控制中的输出频率

3.2 磁链下垂控制仿真结果

图10 为磁链轨迹，其中虚线表示额定磁链轨迹，其幅值的计算公式为：2πfn）≈7.796；实线表示实际的磁链轨迹，仿真得到的平均幅值为7.575，这是因为实际输出无功功率偏离额定值，故磁链的平均值与额定磁链值存在偏差。从图中可以看出采用6 扇区划分时，磁链轨迹近似为圆形，这说明电压被控制在参考值附近。但是由于采用滞环控制，磁链存在脉振，这会间接地影响系统输出电压的质量。

图10 磁链下垂控制中的磁链轨迹

采用磁链下垂控制得到的电压波形如图11 所示。从图11（a）所示，系统电压在0.04 s 的时间内达到稳定。0.15 s 时，R2投入，因为无功负荷不变，故电压幅值无明显变化。另外，从图中可以看到0.15 s 前后波形质量存在比较明显的差异，这说明磁链下垂控制对负荷变化比较敏感。对负载变化前后电压进行谐波分析（分别取t=0.1 s，t=0.2 s），可以看到负载变化前电压总的谐波畸变率为2.09%，变化后谐波畸变率为1.20%，电压质量符合要求，如图11（b）所示。系统电压的动态响应速度低于传统的电压下垂控制，电压畸变率也比传统的电压下垂控制高。

图11 磁链下垂控制中的输出电压

图12（a）为磁链下垂控制中系统输出的电流波形。与电压类似，电流也在0.04 s 内达到稳定。t=0.15 s 时，有功负荷增加，相应的电流幅值增大。对负载变化前后电流进行谐波分析（分别取t=0.1 s，t=0.2 s），可以看到负载变化前电流总的谐波畸变率为1.32%，变化后谐波畸变率为0.84%，电流波形符合要求，但是电流畸变率比较高。

图12 电压下垂控制中的输出电流

图13 为磁链下垂控制中系统输出的频率波形。从图中可以看到：频率位于额定值附近，偏差量很小。即使t=0.15 s 有功负荷增加，频率出现暂时下降，最终也会恢复到额定值附近，系统稳定后频率偏差近似为零。从频率图中可以看到频率不是一个稳定不变的数值，而是在不断地微小波动，这是由相角在滞环范围内的波动引起的。但是由于被紧密控制，故频率变化范围很小。采用相角控制避免了频率的直接下垂，从而有效地减小了频率偏差，提高了电能质量。这是磁链下垂控制优于传统电压下垂控制的地方。

图13 磁链下垂控制中的输出频率

4 结论

本文对两种下垂控制策略进行了深入的对比分析，得出了以下结论：

在传统的电压下垂控制中采用“功率-电压-电流”三环控制策略，需要复杂的参数调试过程。直接频率下垂导致系统输出频率较大程度地偏离额定值，影响电压质量。但是该控制策略的动态响应速度较快、跟踪效果好，能在较短的时间内建立系统的电压、电流平衡。同时具有良好的静态稳定性，电压、电流输出波形良好，谐波畸变率很小。

在磁链下垂控制中采用了DFC，避免了复杂的参数整定过程，大大减小了控制的难度。相角下垂取代频率下垂从而实现了频率的微小偏差甚至零偏差。但是由于采用了滞环控制，导致输出的电压、电流特性不如传统的电压下垂控制，谐波畸变率较大，响应速度也比较慢。

以上两种方案各有优劣，但均能在孤岛系统内建立稳定的电压。需要根据微电网内具体的电压质量要求选择合适的控制方案。