离散S曲线算法控制的机械手臂运动特性研究∗
刘晓飞 高兴华 郭庆东 崔金鹏
(北华大学机械工程学院,吉林省吉林市 132021)
机械手臂作为机器人的末端执行机构[1-4]已在一些流水线生产中得到广泛应用[5]。在智能化生产中,步进电机是主要的驱动部件之一[6],作业时其运行的精确性和响应速度尤为重要。由于步进电机受脉冲频率控制,其高速时的运动特性易对生产线上的装配动作如抓、卡、拧工件等产生冲击,从而造成位置错移,甚至结构变形等。为确保生产线正常运转,通常采用降低生产线速度的方式以避免问题的发生,但因此会影响生产效率[7]。针对以上问题,刘静等[8-11]对步进电机的应用特性进行了研究与改进,以提高智能化生产效率。
合理控制频率可为步进电机提供平稳的工作特性,频率过低或过高均会影响步进电机输出特性,产生低频振荡或高频振动。步进电机低频振荡是由于电机的转子达到稳定平衡位置时具有多余的动能[12]。当控制脉冲的频率等于自由振荡频率时,就会发生低频振荡。而当控制脉冲的频率很高时,脉冲间隔的时间很短,电机转子尚未到达第一次振荡幅值,下一个脉冲就到来,如此会产生失步,甚至还会产生高频振动。
为提高步进电机在智能生产线装配中的工作性能,消除振荡与振动的产生,研究适合不同生产需求的输出特性,本文采用正交两指机械手臂,以步进电机为动力,研究以S曲线算法作为机械手臂控制算法的运动控制,通过合理设计每一个脉冲的升、降频,保证步进电机不堵转、不失步、不过冲,使机械手臂以最少的时间精确运行至指定位置。
1 正交两指机械手臂的组成与输出控制
1.1 机械手臂组成
机械手臂由步进电机、气滑环、滑台气缸和机械手指组成,如图1 所示。

图1 正交两指机械手臂结构图Fig.1 Structural drawing of orthogonaltwo-finger manipulator
步进电机为机械手臂提供旋转动力,带动气滑环、滑台气缸和机械手作旋转运动。气滑环在旋转的同时传递气路,通过气动回路控制机械手作夹持动作。
1.2 步进电机电脉冲加速控制算法
常见的步进电机速度控制算法有梯形曲线算法、指数型曲线算法以及S曲线算法。
梯形曲线具有运算简单[13]等特性,但存在加速突变、运行不稳定等问题,适用于低精度场合。指数控制算法曲线实现繁琐[14-15],适用于高精度场合。S曲线算法的核心在于防止加速度产生突变,减小冲击,并使步进电机运动具有快速平稳的特性,常被应用于精确控制[16];以低频启动,高频率降频实现减速[17],以此达到快速响应的要求。
步进电机转矩与输入的脉冲频率在电流等参数不变的情况下一一对应,为实现输出特性的柔顺平滑,利用数字控制器将连续S曲线函数转换为离散S曲线函数,使步进电机的每个控制脉冲成为频率可调的S离散信号,从而达到对步进电机输出特性的良好控制。
2 S曲线设计与离散化
2.1 S曲线设计
S曲线的函数为Logistic函数,Logistic函数是一个严格的递增函数,图形为一个连续光滑的 S 形,其函数定义式为:

式中:a为控制曲线倾斜的斜率参数[18-19]。设脉冲频率为f(kHz),则

式中:n为电机转速,r/s ;P为细分倍数。
由式(2)可得出步进电机最小启动频率fmin(kHz),以及运行最大频率A(kHz)。
设步进电机运行频率为f(t)(kHz),则
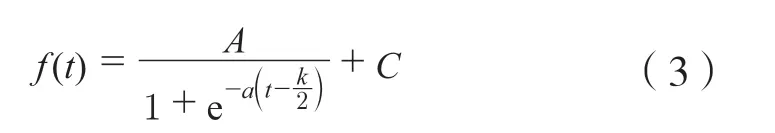
式中:a为斜率常数,是决定运动快慢时间的关键因素;t为电机运行时间,s;k为达到A的时间,s;C为常数。
步进电机是一种数字电动机,可作为数字控制系统中的执行元件,步进电机将输入的脉冲电信号变换为阶跃性的角位移或直线位移[20-21]。其角位移与脉冲数成正比,电机的转速和脉冲信号成正比,通过改变频率的高低即可改变电机的转速[22-25]。
根据步进电机的转矩频率特性曲线可知,在电流不变的情况下,当脉冲频率增加时,电机铁芯中的涡流损耗随之增加,输出功率和转矩下降,使步进电机频率随输出转矩的增大而减小。当输入脉冲频率增加到一定值时,步进电机将无法带动任何负载,而且只要受到很小的扰动,就会振荡、失步,甚至停转。
步进电机的运动方程,即
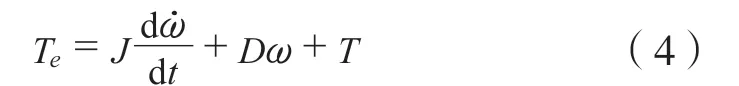
式中: Te为步进电机的电磁转矩,Nm;J为步进电机的转动惯量,kg·m2;D为系统粘性阻尼系数;T为输出转矩,Nm;ω为电机瞬时角速度,rad/s。
ω与f成正比关系,即

式中:Q为线性系数,Q=2π。
电机从静止开始加速,即t=0 时,ω=0,则联立式(3)(4)(5)得:
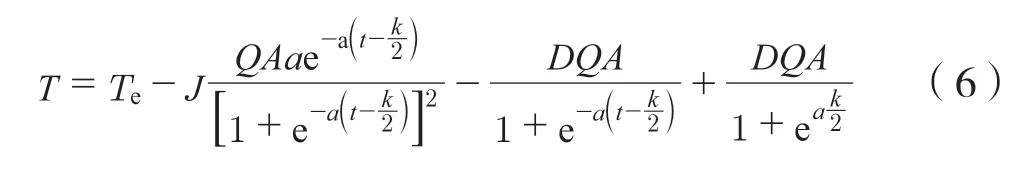
以正转90°为例,根据步进电机的参数以及不同的斜率常数a计算得出多组频率曲线,如图2 所示。

图2 不同斜率常数a下的频率曲线Fig.2 Frequency curve under diあerent time constant a
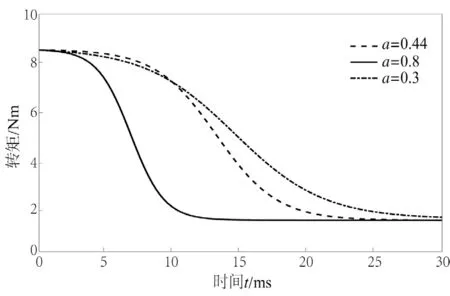
图3 不同斜率常数a下的转矩曲线Fig.3 Torque curve under diあerent time constant a
转矩曲线如图3 所示,在不同斜率参数a下转矩的单位时间变化率不同,电机分别在13、22 ms与28 ms时,频率达到最大,转速最快,转矩最小,符合电机运动规律。
一般情况下S曲线分为 “三段”,即加速、匀速和减速阶段,但当步进电机转过的角度很小时,运动曲线只需要两段,即加速和减速阶段。电机先加速再减速,此曲线为前半段加速曲线;减速阶段和加速阶段类似,可以分别单独在软件编程中做一个数组,也可以和加速阶段共用一个数组。
2.2 S曲线的离散与优化
输入步进电机参数,得到频率曲线,并利用改进欧拉递推方法获得离散频率。设微分方程为:

设时间区间为[a,b],从区间中取离散的点
取k=0,1,2,…,N,从t0开始,逐渐递推求解t1时的y1,t2时的y2,…,直至tn时的yn。
其改进欧拉递推公式为:

式中:h=tn+1-tn。
设置优化曲线的约束参数条件,细分倍数P、最小启动频率fmin、最大运行频率A,时间区间为[0,30],离散点数为100。得到a=0.44 时的离散频率曲线如图4所示。
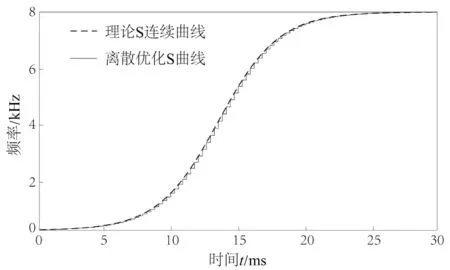
图4 连续频率曲线与对应的优化离散频率曲线Fig.4 Continuous frequency curve and the corresponding discrete frequency curve
确定定时器的自动重装值。本试验机械手臂的控制器为STM32,将STM32 的定时器设置为溢出中断模式, 定时器的溢出中断周期由时钟预分频数和自动重装值决定,固定预分频数后,中断周期由自动重装值决定。
将计算得到的离散频率值处理为数组保存于控制器中,控制器按顺序读取数组里的频率值进行定时器计数值重装载。根据不同时刻的频率,对应不同的自动重装载值,从而实现S曲线离散化。
3 离散优化S曲线仿真
3.1 试验系统组成
本试验的机械手臂使用86 系列步进电机,选用HB860 驱动器。气缸选用型号MHF2-8D1R的滑台气缸,行程为260 mm。试验所用三阶魔方为市面比赛专用魔方,材料为ABS塑料,摩擦系数为0.48,边长为57 mm。手臂模型如图5 所示。

图5 正交两指机械臂三维建模图Fig.5 3D modeling diagram of orthogonal two-finger manipulator
机械臂控制核心采用STM32F407,通过定时器输出PWM波调控电机运动,利用I/O口控制电磁阀换向,实现机械手爪动作。
3.2 离散优化S曲线应用仿真
建立步进电机平衡方程,并在MATLAB中搭建仿真模型,如图6 所示。
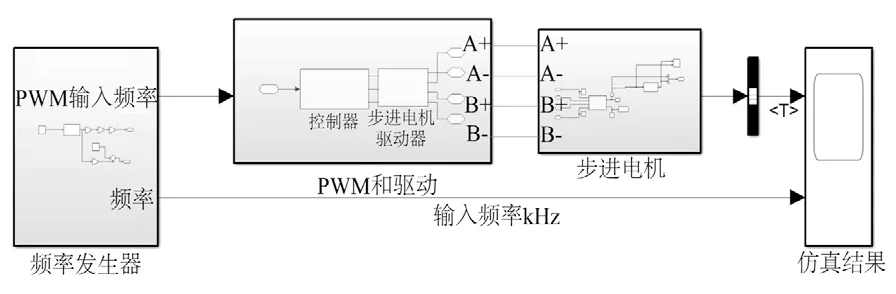
图6 系统仿真建模Fig.6 System simulation modeling
频率发生器输出离散的频率数组,通过PWM得到不同频率的方波,输入到驱动,驱动电机输出转矩仿真结果。根据不同斜率系数a得到相应的转矩曲线图,如图7 所示。
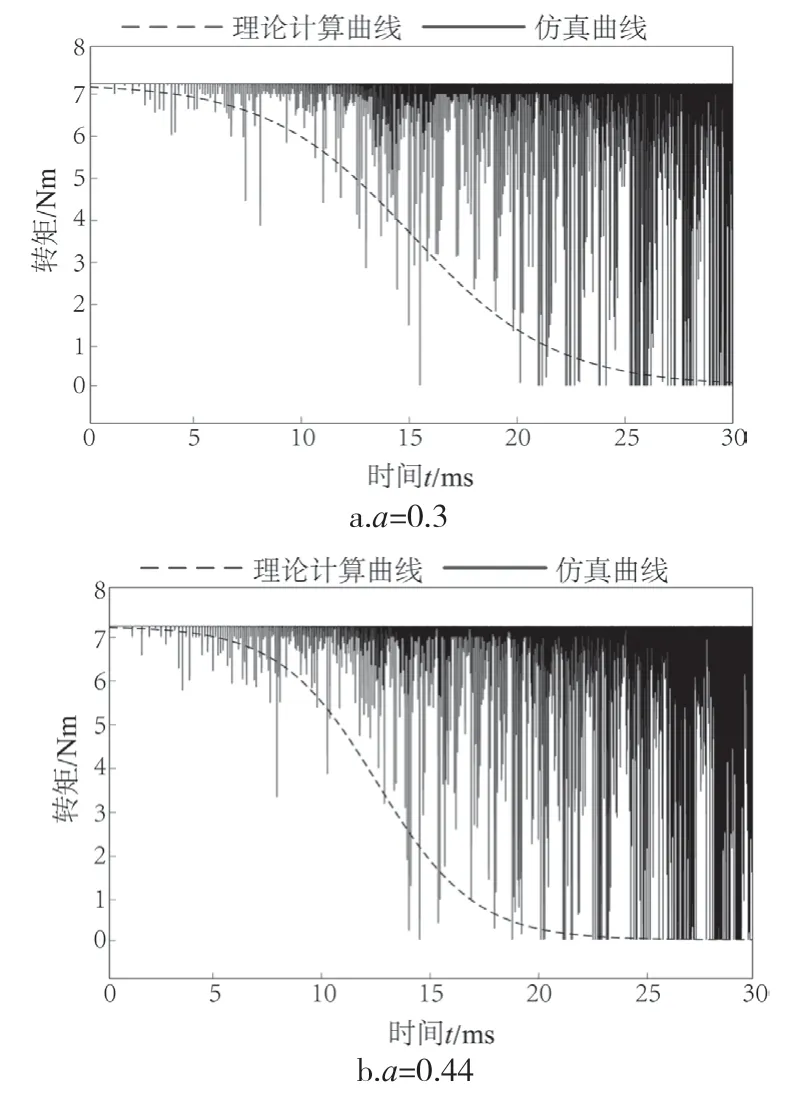
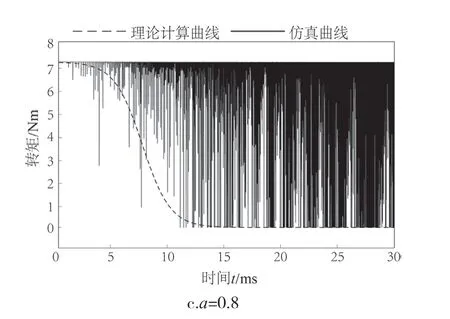
图7 不同斜率常数所对应的转矩曲线图Fig.7 Torque curve corresponding to diあerent slope constants
仿真结果表明,电机在22 ms,频率达到最大,转矩达到最小,此时转速最大,加速度最大;当a为0.3 时,频率与转矩的单位时间变化率较小,因此加速时间较长,如图7a所示;当 a为0.8 时,频率与转矩的单位时间变化率较大,导致电机发生失步,如图7c所示。理论计算输出的转矩曲线与仿真曲线拟合度基本一致,其中误差由软件处理所致。
4 应用试验测试
将机械手臂应用于魔方机器人上进行测试,机械手臂试验平台如图8 所示。

图8 魔方机器人试验平台Fig.8 Rubik's cube robot test platform
以带载正转90°为例,采用2.2 章节计算优化后的3 组离散S曲线,其中a=0.44 时的曲线如图9 所示。
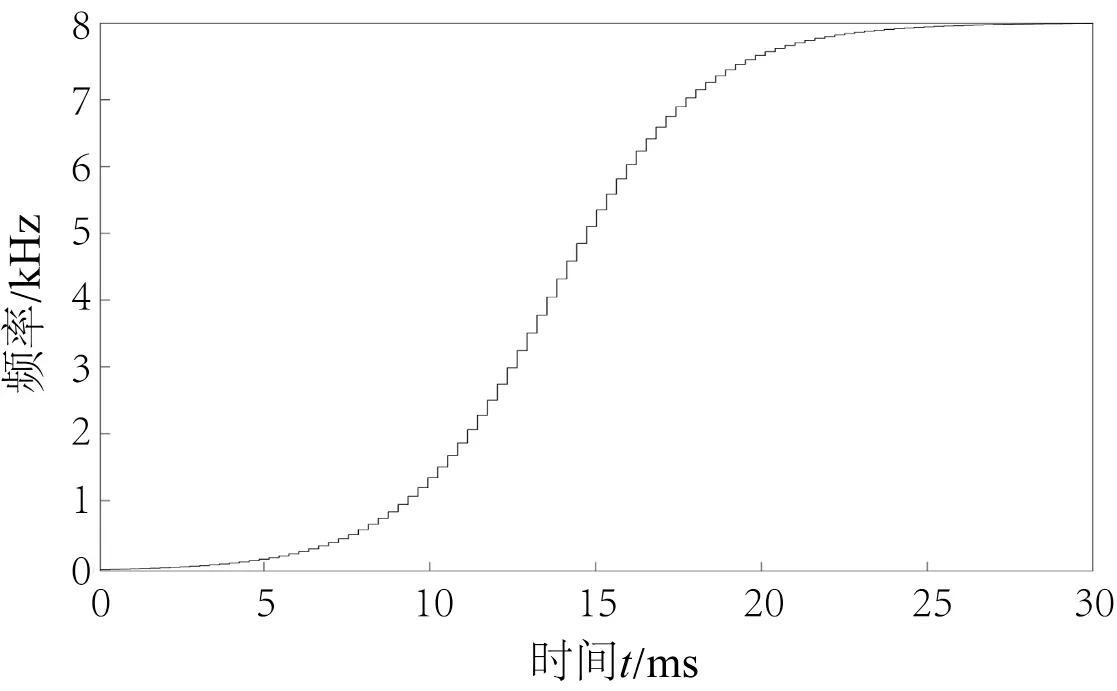
图9 优化后的S曲线图Fig.9 The optimized S-curve
离散点数为100,分别输入到控制器中,读取试验数据,与仿真数据进行对比。对比结果如表1 所示。
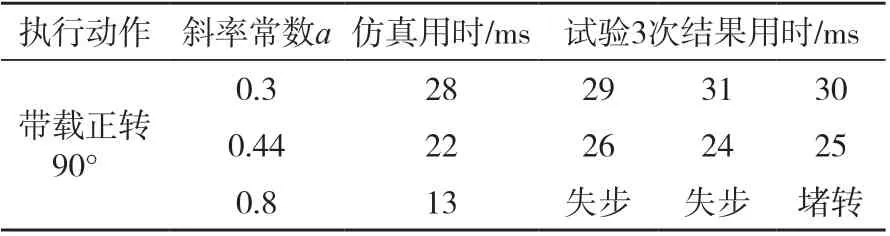
表1 仿真用时与试验用时对比Tab.1 Comparison of simulation time and experiment time
测试结果表明:电机带载正转90°时,斜率常数等于0.3 时,电机运行时间并未达到最短;斜率常数等于0.44 时,运行平稳,时间短,且不发生失步及过冲;而斜率常数等于0.8 时,由于频率提升快,导致失步,严重时堵转,致使电机平稳后并未达到期望转角。
5 结论
本文结合实际需求,研究将离散S曲线算法用于步进电机输出平滑转矩控制,算法在还原魔方机械臂调控中应用,达到了速度快、精度高的效果。该方法通过合理设计每个脉冲频率的升、降,有效防止了步进电机失步、过冲等现象,并且使步进电机能以最快的响应速度执行动作。算法理论可推广应用于不同的步进电机,通过优化理论方程中的参数,确定适用于不同环境下步进电机的S曲线,经过离散处理后控制步进电机的运动,可以实现不失步、不过冲,达到快速、精准控制的目的。S曲线算法是一种全新的步进电机调速算法,适用于机械手装配柔性动作等控制。

