双自由度子母管线涡激振动数值研究

蒋昌波， 徐进， 屈科

(1.长沙理工大学 水利工程学院，湖南 长沙 410114； 2.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114； 3.洞庭湖水环境治理与生态修复湖南省重点实验室，湖南 长沙 410114)

近年来，为满足海洋油气工程的需要，工程人员设计了一种新型的海底管线称为“子母管线”。其常见的布置是将2条不同直径的管线平行地捆绑为一个整体，其中直径大的母管用于传输油气，直径小的子管线用来安装监测、通信设施或传输置换介质[1]。相比传统的海底管线，这种子母管线不仅更加安全，而且可以节省大量的工程建设费用，降低时间成本[2]。子母管线的布置是工程上比较关心的问题[3]，子母管线相对位置会直接影响其水动力特性。因此对子母管线的振动特性进行系统的研究有助于确定合理的子母管线布置，为工程实践提供设计方案。

国内外的学者针对单管线和等直径双管线的水动力特性开展了系统的实验[4-6]和数值模拟研究[7-9]，但是对于不等直径双管线的振动特性研究较少。早期，学者们对子母管线的研究主要针对空间固定的管线[10]，不考虑子母管线的运动，没有系统研究子母管线的涡激振动特性。然而涡激振动是导致海底管道疲劳断裂的主要原因[1]，因此需要对子母管线的涡激振动特性进行研究。Zang等[11-12]采用实验手段研究不同布置条件下的单自由度子母管线尾涡强度和管线振幅的变化规律，分析了子母管线的布置对其涡激振动的抑制作用，找到最优的子母管线布置方案。但是这些研究只考虑了管线的横向运动，忽略了子母管线在流向的振动过程。然而，相比管线的横向振动，流向振动对管线的破坏作用也不可忽略[13]。而且，在子母管线小质量比的情况下，管线的横向运动和流向运动存在明显的耦合效应[14]。因此有必要对子母管线双自由度涡激振动特性进行深入研究。

为了弥补现有研究不足，本文采用高精度浸没边界方法的数值模拟了低雷诺数下(Re=150)双自由度子母管线的涡激振动现象，对比单自由度和双自由度情况下子母管线涡激振动特性的区别，分析不同的管线布置对双自由度子母管线振动特性和锁定区间的影响。

1 数值方法

1.1 控制方程

对于流固耦合问题，其不可压缩流的连续性方程和动量方程分别为：

(1)

(2)

式中：ui为笛卡尔坐标系下的流速；p为真实压强除以密度ρ；雷诺数Re=UD/υ；U为流体的速度；υ为动力粘度；D为特征长度。

假设圆柱用弹簧固定，考虑结构阻尼，其运动控制方程为：

(3)

式中：对于物体平动；M为质量；Yi分别为x、y2个方向上的位移；C为阻尼因子；K为弹簧的劲度系数；Fi分别为x、y2个方向上所受到的水流力。

物体与流体交界面上的边界条件为：

(4)

为了求解式(3)，将其转化成一阶常微分方程：

(5)

(6)

1.2 流固耦合求解

式(3)右侧流体作用在物体上的力矢量F是位移Y和流场信息w的函数，式(3)可以改写成：

(7)

式中:w为包含所有流场变量的向量，即w=(up)T。将式(7)半离散为：

(8)

式中：a和b为常数(a+b=1，a>0，b>0)，若采用松耦合(显式)求解，则b=0，若采用强耦合(隐式)求解，则b≠0。本文主要探讨松耦合情况：

1)根据已知物体位置Yn，即物体边界条件，通过求解式(2)得到un+1和pn+1；

2)利用n步的位置Yn和n+1步的流场向量wn+1计算得到物体上受到的力(或力矩)，F=F(Yn,wn+1)；

3)

(9)

(10)

通过式(9)、(10)离散格式求解式(8)得到Yn+1，实现浸没边界方法重要的一步是将网格节点分为流体、边界和物体内部网格，如图1所示。物体周围网格节点作为边界节点需要进行边界条件重构，边界外的网格节点为流体，而物体内部的节点不参与计算，详细的数值方法参考文献[15]。

图1 浸没边界网格划分Fig.1 The schematic of immersed-boundary grid

1.3 无量纲化

将式(3)的变量无量纲化，得到：

(11)

2 模型验证

当圆柱的自然频率与涡脱落频率一致时，发生锁定现象，此时圆柱有较大的振幅。为了验证本模型模拟涡激振动问题的准确性，采用与文献[15-16]相同的工况进行验证。计算区域为34D×16D的二维矩形区域，圆柱距离进口和底边界皆为8D。在圆柱周围3D×3D的矩形区域中对网格进行加密，最小网格尺寸为dx=dy=0.02D，计算时间步长为0.008 s。雷诺数Re和圆柱的质量比m*不变分别为150和2，改变圆柱的约化速度Ur，并将计算结果与文献[15-16]的结果进行对比。图2展示了最大横向振幅与约化速度的关系，图中的Ay为最大横向无因次振幅，Ay=(ymax-ymin)/2D，其中ymax和ymin分别为横向位移的最大值和最小值。从图中可以看出本模型的计算值与文献[15-16]结果吻合度高，圆柱的锁定区域为3.5≤Ur≤7.5。通过验证可以证明本模型能够准确地模拟出圆柱涡激振动的振幅和锁定发生的范围。

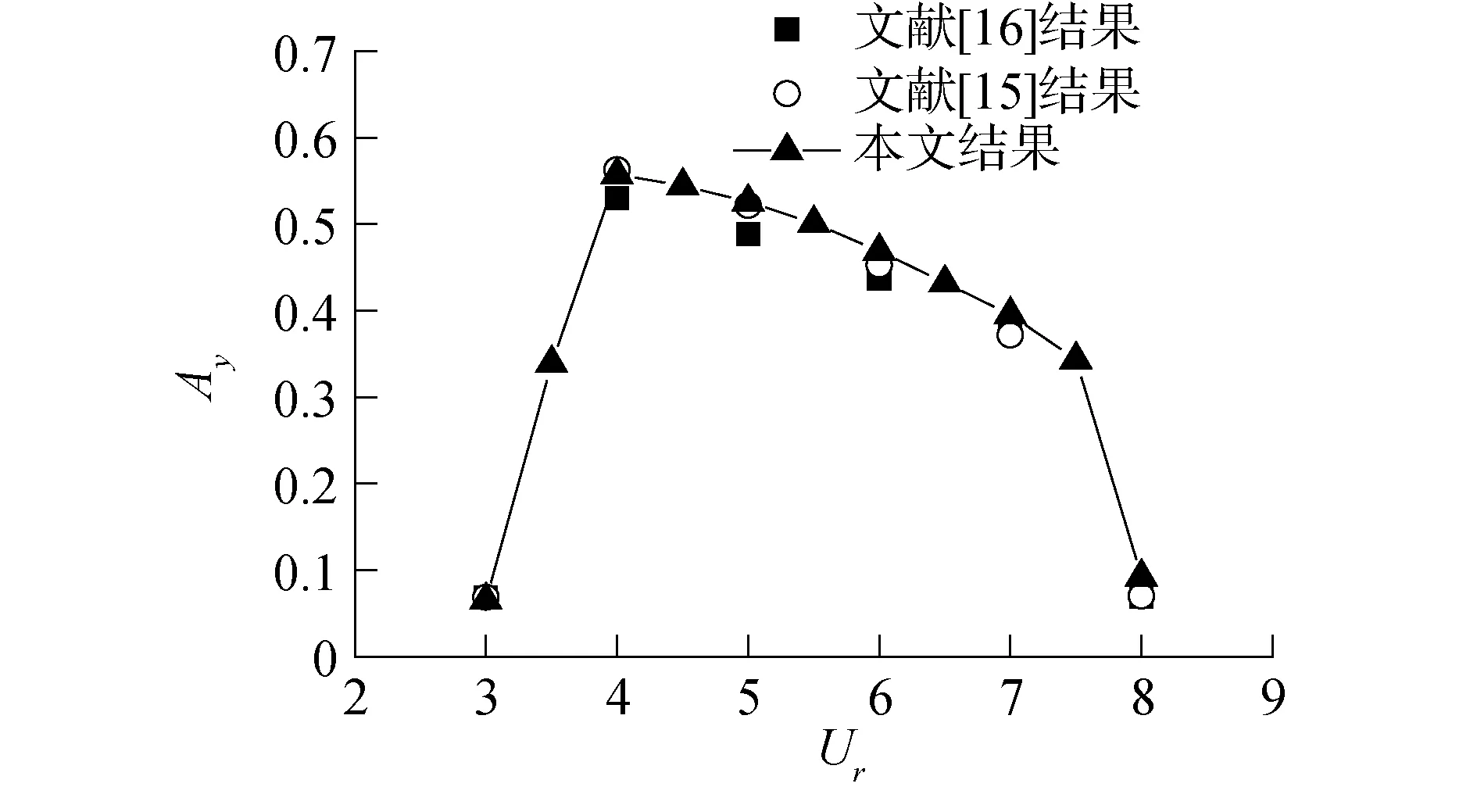
图2 最大横向振幅Ay随约化速度Ur的变化Fig.2 The relationship between the maximum cross-flow amplitude Ay and reduced velocity Ur

3 问题描述

如图3所示，直径为D的大圆与直径为d的小圆捆绑在一起组成一个整体，该整体称为“子母管线”，同时拥有x和y方向2个平动自由度，且在x、y方向具有相同的自然频率。由于子管与母管之间存在刚性连接，因此两者作为一个整体同时运动。坐标原点位于母管圆心处。图中D为母管直径、d为子管直径、G为母管与子管之间的间距，e为母管与床面之间的间隙，θ为母管与子管圆心的连线与x轴负方向的夹角。为了研究子母管线的布置对涡激振动的影响，设置母管与子管的间距比G/D为0.2～0.5、母管与床面之间的空隙比e/D的范围为0.2～1.0、角度θ分别为0°、90°和180°、子母管整体的质量比m*分别为1、2和7。子管直径d=0.5D、雷诺数Re=150和阻尼系数ξ=0.01固定不变。具体计算工况如表1所示。

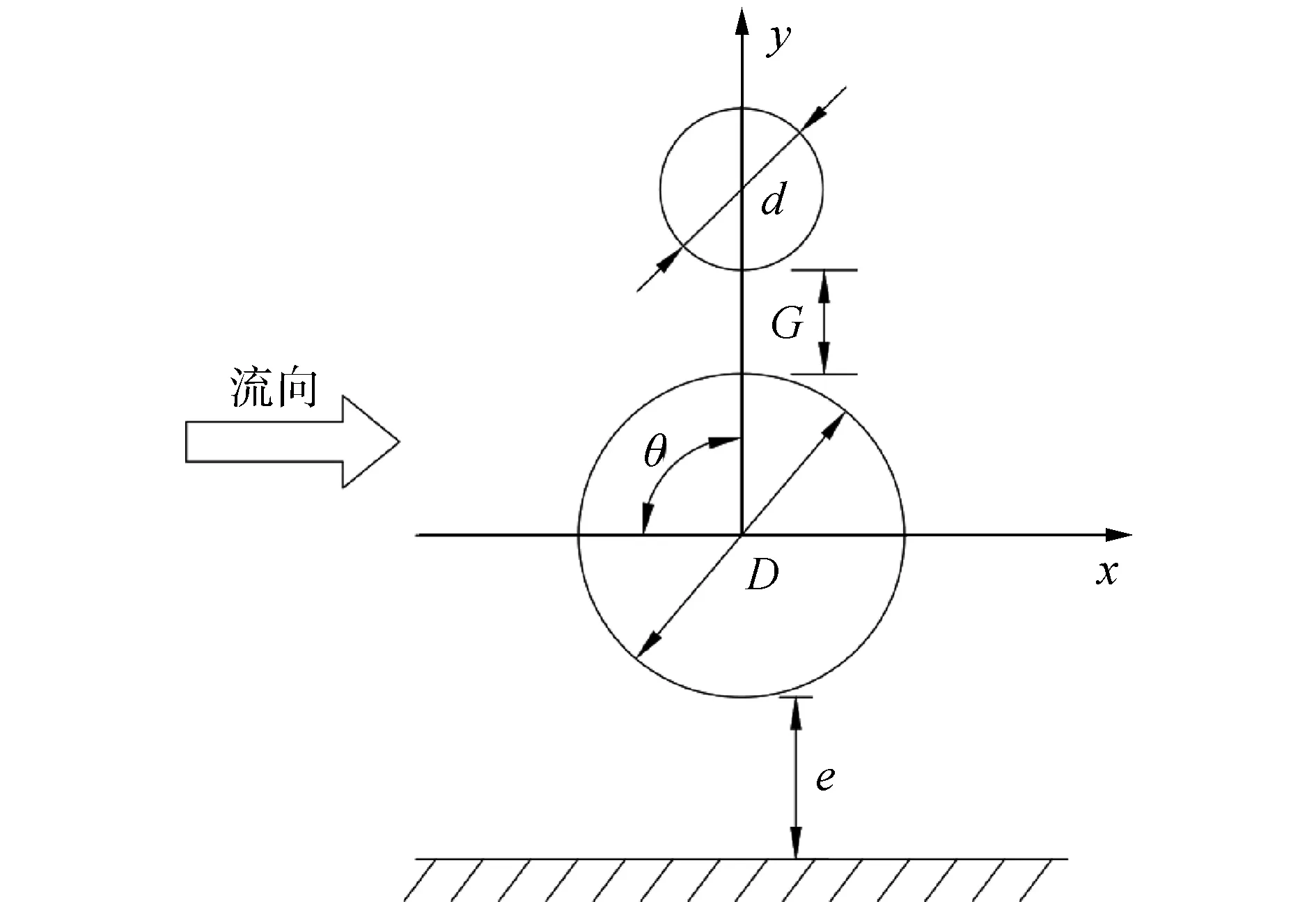
图3 子母管线布置Fig.3 The layout of piggyback pipeline

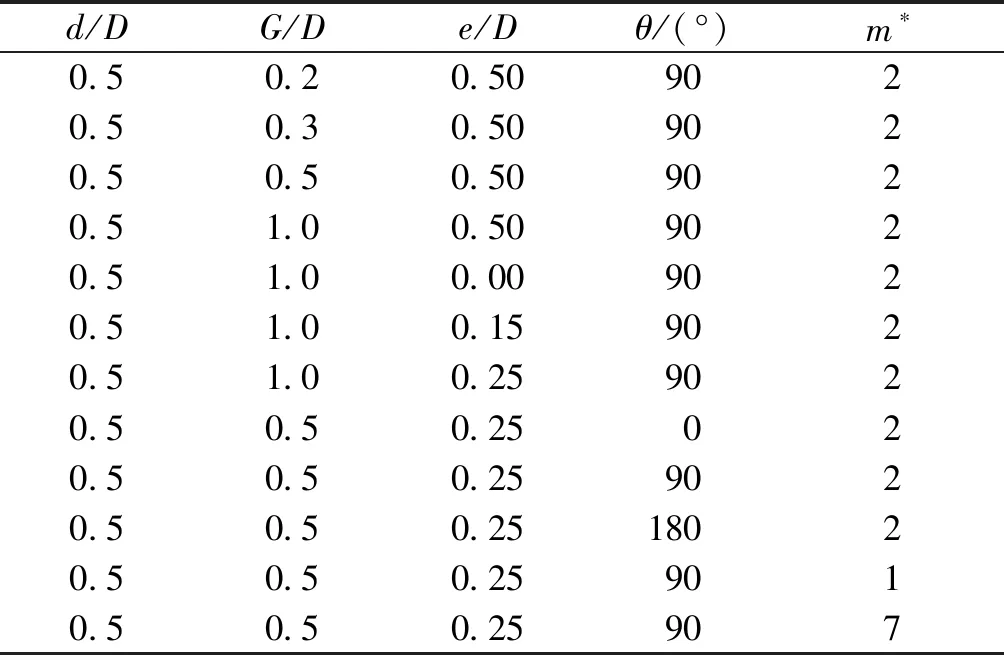
表1 计算工况表Table 1 The computational case

计算区域为35D×10D的矩形区域，母管至进口的距离为10D，母管与床底的空隙e是变化的。在子母管线周围6D×4D的区域对网格进行局部加密，最小网格尺寸dx=dy=0.02D，计算的时间步长为0.008 s。

4 结果分析

4.1 流向振动对横向振动的影响

以m*=1、2、7和Ur=6的工况为例，分析流向振动对横向振动产生的影响。图4(a)给出了m*=1，Ur=6时横向无因次位移随时间变化曲线，图4中A=y/D，其中y为圆柱瞬时位移。此时双自由度管线的最大横向振幅和平均振幅分别比单自由度时大8.1%和14%。除了振幅不同外，双自由度管线的振动频率也略快于单自由度的情况。图4(b)展示了m*=2，Ur=6时横向无因次振幅随时间变化曲线，与m*=1时相同，也是双自由度的管线具有更大的振幅，但是由于质量比的增大，其振幅增大的幅度略有减小，双自由度的管线最大横向振幅和平均振幅分别比单自由度时增大7.9%和12%。图4(c)展示了m*=7，Ur=6时横向无因次位移随时间变化曲线，此时双自由度与单自由度时管线的最大横向振幅和平均振幅的差值均小于1%，且两者具有相同的振动频率。

4.2 质量比对子母管线涡激振动的影响

为了研究质量比对子母管线涡激振动的影响，共设置3个不同的质量比，分别为m*=1、2、7。除了质量比外，其余参数皆不变，即母管和子管的直径比d/D=0.5、子管相对于母管的角度θ=90°、间距比G/D=0.5、空隙比e/D=0.5。

图5(a)展示了不同质量比子母管线的横向最大振幅随约化速度的变化，从图中可看出质量比越小Ay的最大值越大，锁定区间也越宽。当m*=1时，横向最大振幅出现了2个峰值，分别在Ur=6和Ur=13处，而m*=2和m*=7时的最大横向振幅只有一个峰。当m*=2时Ay的最大值与m*=1时的最大值相近，但是其锁定区间较m*=1时有所缩窄。当m*=7时，只在Ur=4和5时出现较大振幅，锁定区间较m*=2时进一步缩窄，此时Ay的最大值只有m*=1时的33.4%。图5(b)展示了不同质量比子母管线的最大流向振幅随约化速度的变化，图中Ax为最大流向无因次振幅，Ax=(xmax-xmin)/2D，其中xmax和xmin分别为流向位移的最大值和最小值。从图中可看出流向振幅与横向振幅有相同的变化规律，m*=1时,出现2个峰值，m*=2,7时,只有一个峰值。通过对比可发现，在该组工况下流向振幅相对于横向振幅是不可忽略的，m*=1,2,7时,Ax最大值分别为Ay最大值的32.4%、20.4%和20.0%。

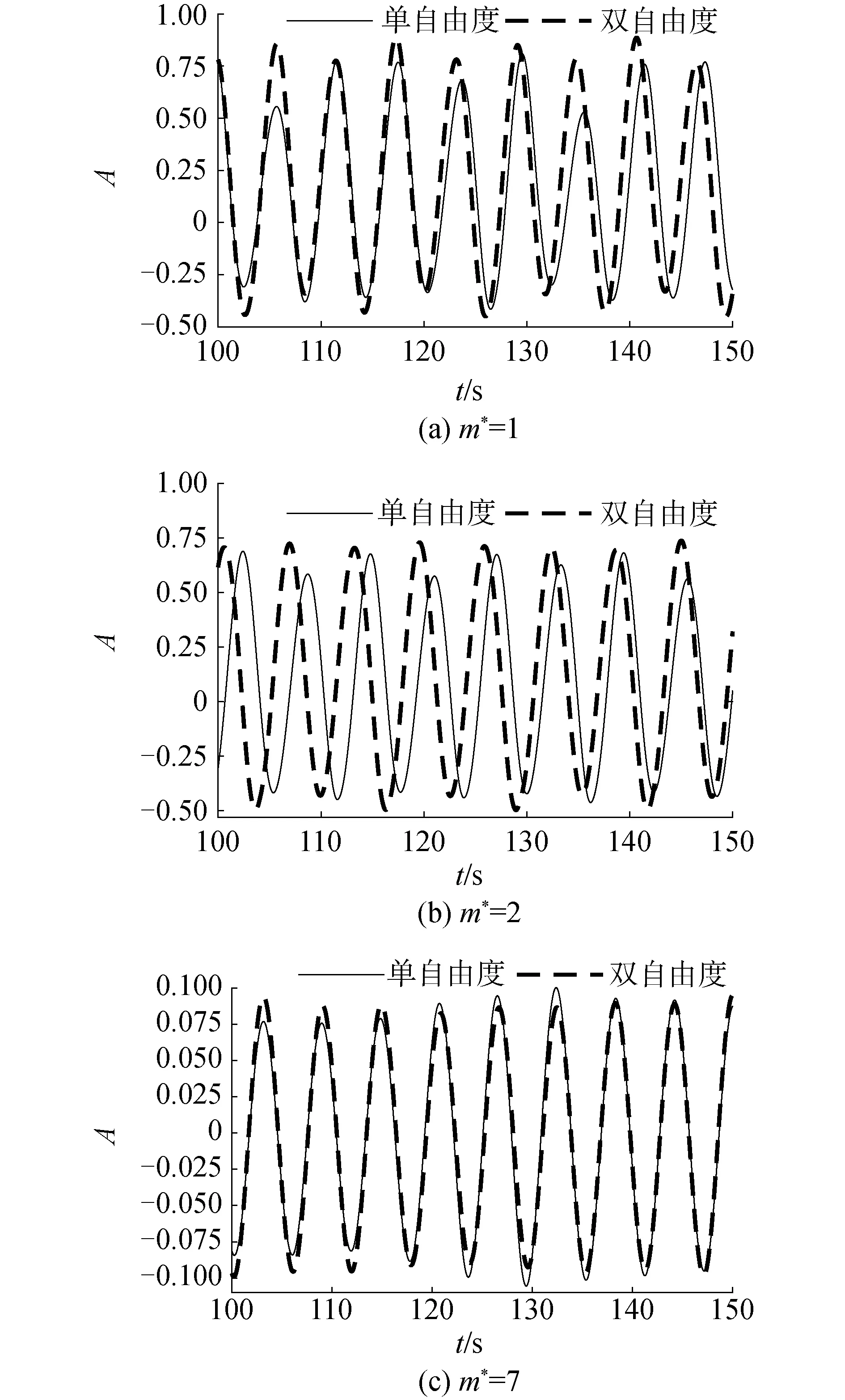
图4 Ur=6时横向位移时程曲线Fig.4 Time history of cross-flow displacement under Ur=6

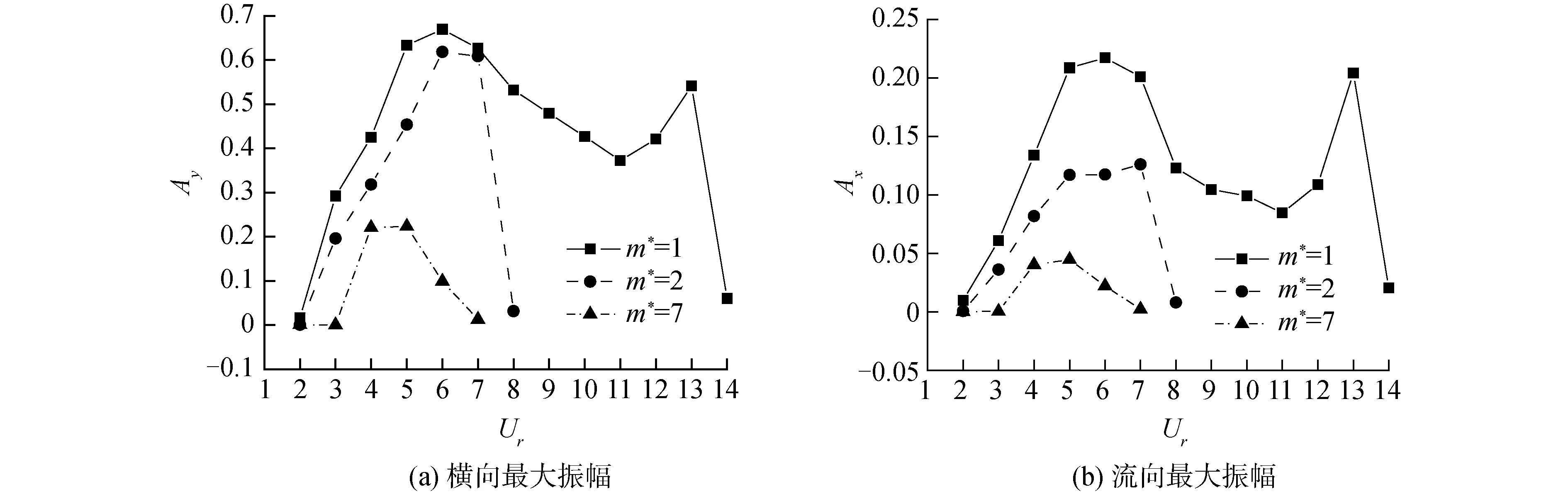
图5 不同质量比情况下最大振幅随约化速度的变化Fig.5 The relationship between the maximum amplitude and reduced velocity under different mass ratio

为了研究质量比对管线振动频率和振动轨迹的影响，以Ur=5的工况为例。图6分别展示了Ur=5，m*=1,2,7时，横向和流向无因次位移的谱分析。从图6(a)看出所有的质量比情况下横向位移的谱只有一个谱峰，而且质量比越小谱峰越高，谱峰频率越小。图6(b)中m*=1和7时的流向位移的谱峰较m*=2时要小，但是从图5(b)可以发现m*=1时的最大流向振幅要大于m*=2，导致m*=1时的谱峰小于m*=2时的原因是:m*=1时出现2个谱峰，分别在f=0.18 Hz和0.35 Hz处，频率分布更分散，而m*=2时只有一个主频，且其振动频率主要集中于主频附近。由于m*=1时有多个不同的振动频率，所以子母管线的振动轨迹没有明显的周期性(图7(a))。而m*=2和m*=7时横向振动频率和流向振动频率相近，因此图7(b)和(c)中的轨迹呈现出“0”字形。

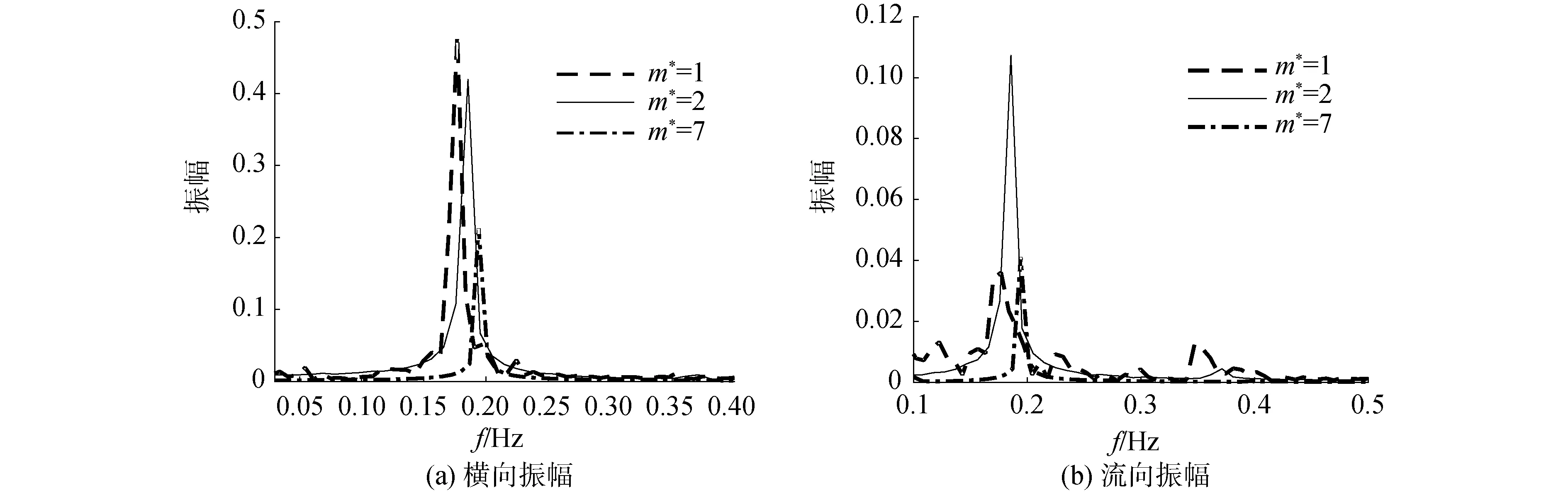
图6 Ur=5时横向振幅和流向振幅的谱分析Fig.6 The spectrum analysis of cross-flow amplitude and down-stream amplitude under Ur=5

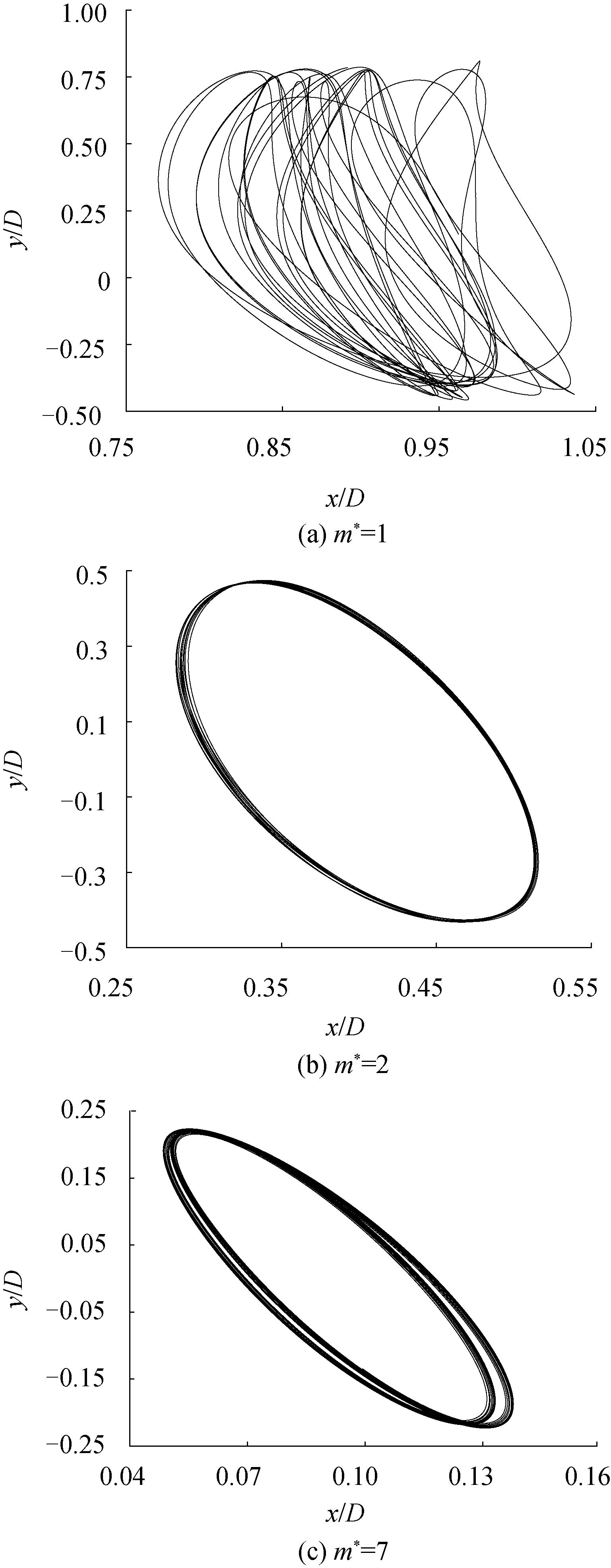
图7 Ur=5，m*=1,2,7时子母管线的运动轨迹Fig.7 The piggyback pipeline movement under Ur=5,m*=1, 2, 7

4.3 间距比对子母管线涡激振动的影响

本节设置间距比G/D分别为0、0.15、0.25、0.50，研究间距比对子母管线涡激振动的影响。直径比d/D、空隙比e/D、质量比m*、子管相对于母管的角度θ皆不变，分别为0.5、1.0、2和90°。

图8展示了最大横向振幅和最大流向振幅随约化速度的变化，从图中可发现间距比不同的情况下出现Ay和Ax峰值时的约化速度是不同的。从图8(a)中发现G/D=0,0.15时,Ay最大值出现在Ur=5处，G/D=0.25,0.50时,在Ur=6处出现Ay的峰值。图8(b)中看出G/D=0,0.15和0.25时,分别在Ur=6、5和5处出现Ax的最大值，而G/D=0.50的流向振幅较小可以忽略。同时，不同间距比子母管线的振幅也不同，子母管线Ay和Ax的峰值均随着G/D的增大而减小，其中G/D=0时Ay的最大值是G/D=0.50时的2.26倍。除此之外，间距比G/D=0时的锁定区间最宽，而G/D=0.15,0.25,0.50时的锁定区间较为接近。

图9分别展示了G/D=0，0.15，0.25，0.50，Ur=5时，子母管线周围瞬时涡量云图。图9(a)中子管与母管的间距比为0，可以看到该工况下的子管与母管作为整体一起脱涡，2个圆柱间的相互干扰较少，导致了G/D=0时出现最大的横向和流向振幅。从图9(b)～(d)中可以看出随着G/D的增大，2个圆柱不再作为整体一起脱涡，子管与母管之间的相互干扰增强。图9(d)中间距比G/D=0.50，子管与母管上均有明显的涡脱落，在此时刻子管的涡向下脱落对母管的脱涡产生了干扰。通过上述的分析可看出，子管与母管之间的间距较小时，2个圆柱作为一个整体，其相互间的干扰较少，从而导致其振幅较大。随着间距的增大，子管与母管各自皆有涡脱落，两圆柱间的相互干扰增强，会对子母管线的涡激振动产生抑制作用，使得振幅逐渐减小。

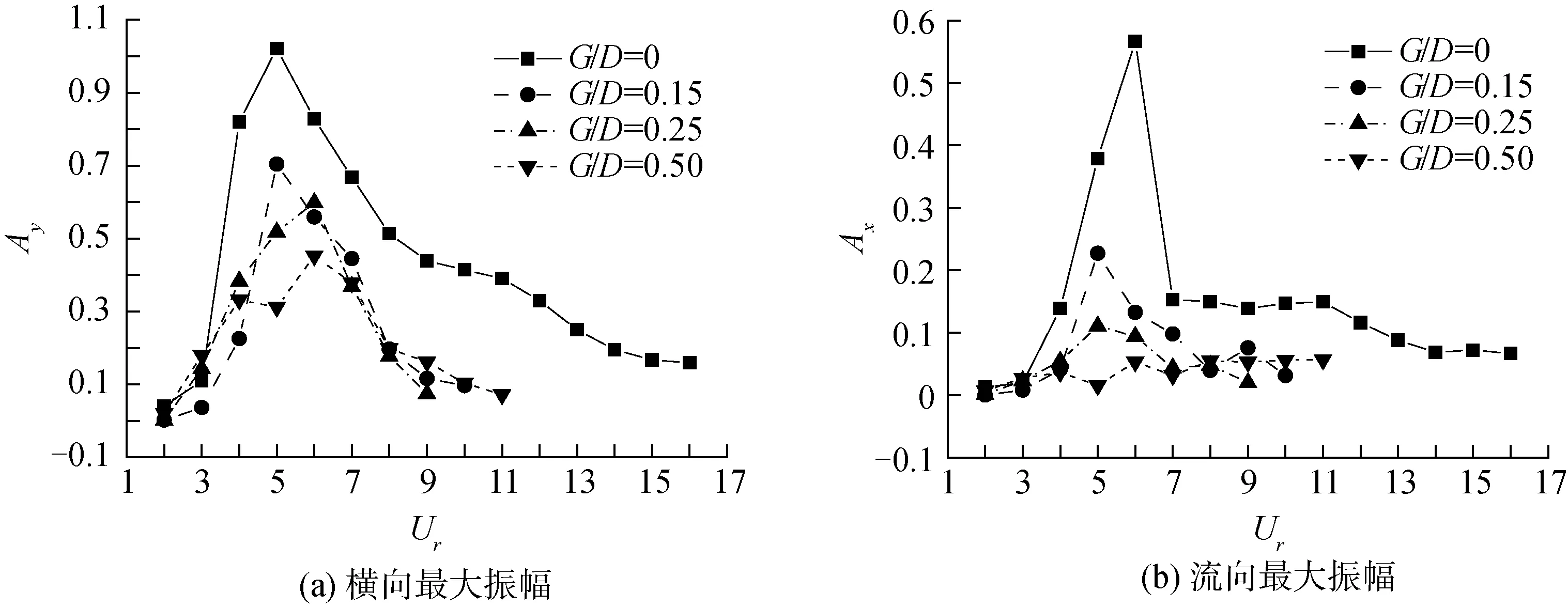
图8 不同间距比情况下最大振幅随约化速度的变化Fig.8 The relationship between the maximum amplitude and reduced velocity under different the spacing-to-diameter ratio

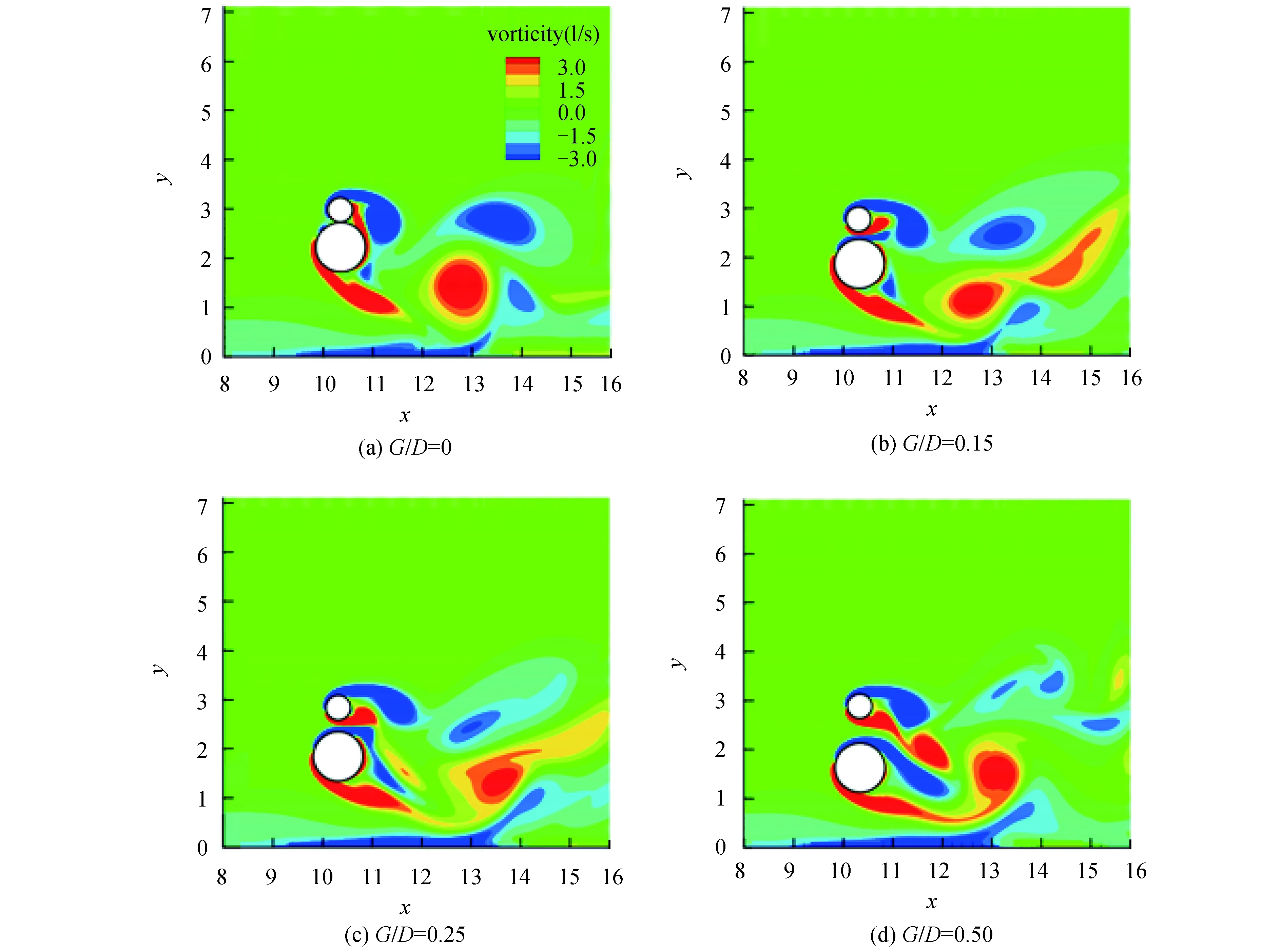
图9 不同间距比情况下子母管线周围瞬时涡量云图Fig.9 The instantaneous vorticity around piggyback pipeline under different spacing-to-diameter ratio

4.4 空隙比对子母管线涡激振动的影响

子管与母管的直径比d/D=0.5、间距比G/D=0.5、子管相对于母管的角度θ=90°、质量比m*=2保持不变，空隙比分别为0.2、0.3、0.5和1.0，研究空隙比对子母管线涡激振动的影响。

图10分别展示了最大横向和流向无因次振幅随约化速度的变化。从图10(a)中可看出，不同的空隙比情况下，出现Ay最大值时的约化速度是不同的，e/D=0.2，0.3，0.5，1.0时出现横向最大振幅峰值的约化速度分别为Ur=8，7，5，6。此外，所有的空隙比情况下Ay的峰值相差较小。图10(b)中发现所有的工况下流向振幅均比较小，可以忽略。

图11分别展示了子母管线振动的横向和流向振动平衡位置，图中的Px=(xmax+xmin)/2D和Py=(ymax+ymin)/2D，分别为x和y方向的平衡位置。从图11(a)中可以看出e/D=0.5和1.0时，管线横向振动的平衡位置更接近于初始位置(Py=0)，而e/D=0.2和0.3时，管线的平衡位置比e/D=0.5和1.0时偏上些，这是由于管线离床面近使其向下振动的过程受到了床面的抑制。图11(b)中的流向平衡位置与空隙比无关，而随着约化速度的增大不断增大。

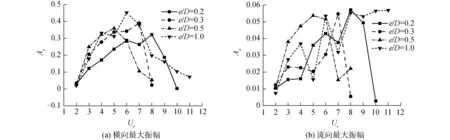
图10 不同空隙比情况下最大振幅随约化速度的变化Fig.10 The relationship between the maximum amplitude and reduced velocity under different the gap-to-diameter ratio

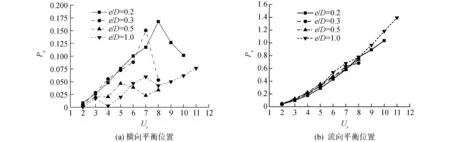
图11 不同空隙比情况下横向平衡位置和流向平衡位置随约化速度的变化Fig.11 The relationship between the cross-flow mean position， down-stream mean position and reduced velocity under different the gap-to-diameter ratios

4.5 角度对子母管线涡激振动的影响

为了研究角度对子母管线涡激振动的影响，改变子管与母管的相对角度，θ分别为0°、90°和180°。保持子母管线管的直径比d/D=0.5、间距比G/D=0.5、质量比m*=2和空隙比e/D=0.5不变。

图12分别展示了θ=0°，90°，180°时横向最大振幅和流向最大振幅随约化速度的变化。从图12(a)中可发现θ=90°即双圆柱并列时，最大横向振幅的峰值出现在Ur=6处，其峰值是θ=0°和180°时的2.5倍以上。当θ=0°即子管位于母管上游时，子母管线的Ay较小而且只有很窄的锁定区间，只在Ur=4和5的情况下出现较大振幅；当θ=180°即子管位于母管下游时，Ay的峰值与θ=0°时相近，但是其锁定区间更宽。从图12(b)中看出θ=90°时最大流向振幅与最大横向振幅相差较大，Ax的峰值只有Ay峰值的20.4%，而θ=0°和180°时的最大Ax的最大值占到Ay最大值的50%以上。

图12 不同角度情况下最大振幅随约化速度的变化Fig.12 The relationship between the maximum amplitude and reduced velocity under different angles

图13分别展示了θ=0°,90°,180°，约化速度Ur=5时，子母管线周围的涡量云图，其中图13(a)、(b)、(c)中的子母管线处于上升趋势，图13(d)、(e)、(f)处于下降趋势。图13(a)、(d)中母管位于子管的下游，母管有涡脱落，而由于两圆柱的间距小于子管尾涡的长度，使得子管的脱涡受到母管的抑制。图13(b)、(e)中的母管和子管皆有涡脱落，当子母管线处于上升阶段时，圆柱的涡向下脱落，而当子母管线处于下降阶段时，圆柱的涡向上脱落，可看出在运动过程中子管与母管脱涡相互干扰。图13(c)、(f)中子管位于母管的尾涡区中，受到母管尾涡的屏蔽，子管上没有涡脱落，同时由于子管的存在对母管的脱涡产生了干扰。通过上述的分析可得出在该组工况下，子管和母管串列时两圆柱之间的干扰对子母管线涡激振动的抑制作用更强，而子管与母管并列时的干扰相对较弱，因此并列情况下子母管线有更大的振幅。

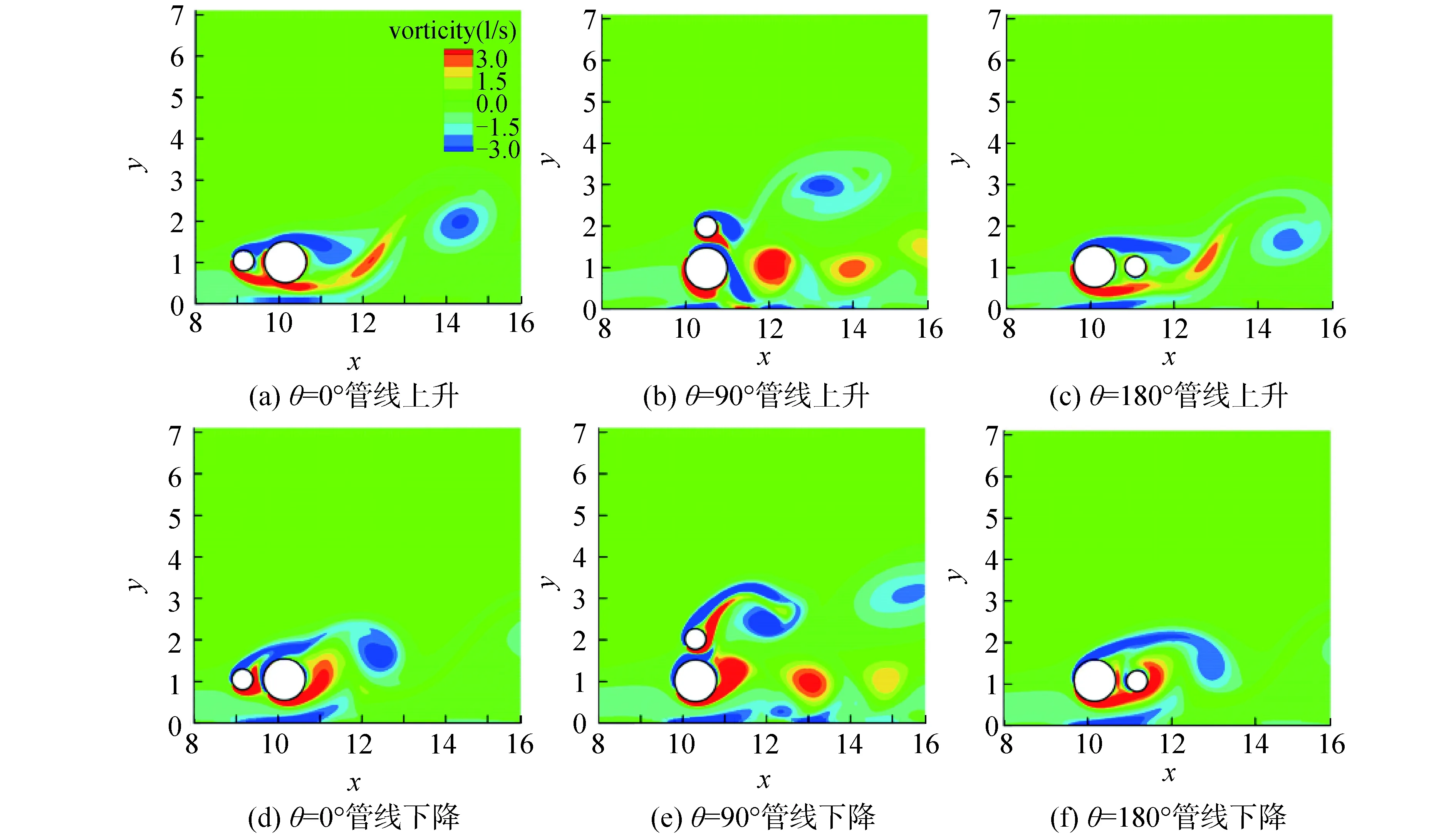
图13 不同角度情况下子母管线周围瞬时涡量云图Fig.13 The instantaneous vorticity around piggyback pipeline under different angles

5 结论

1)低质量比时流向自由度对子母管线的横向振动的影响较大，导致双自由度的子母管线比单自由度时具有更大的横向振幅。此外，随着质量比的增大，双自由度子母管线的横向振幅和流向振幅的峰值均减小，而且锁定区间也逐渐缩窄。

2)在间距比G/D=0时，子管与母管作为一个整体一起脱涡，相互之间的干扰较小，导致了子母管线有最大的横向和流向振幅。而随着间距比的增大，子管与母管之间的干扰增强，管线的最大振幅逐渐减小。尤其是当间距比为0.50时，管线上的流向振幅很小，可以忽略。

3)空隙比对子母管线最大横向振幅的影响相对较小，但是会导致出现最大横向振幅峰值时的约化速度不同。流向平衡位置与空隙比是无关的，而横向平衡位置与其有关，当空隙比较小时，床底会抑制子母管线向下的振动，导致管线的平衡位置相对偏上。

4)通过分析可以看出θ=90°时，子母管线上最大横向振幅的峰值最大，是θ=0°和θ=180°时的2.5倍以上，说明子母管线并列时对子母管线涡激振动的抑制作用更强。